贪心（区间问题 Huffman树 排序不等式 绝对值不等式 推公式）

---

区间问题

常用排序操作

• 按左端点排序
• 按右端点排序
• 双关键字排序（先按右端点，再按左端点）

区间选点

题目描述：
给定 $N$ 个闭区间 $[a_i,b_i]$，请你在数轴上 选择尽量少的点，使得每个区间内至少包含一个选出的点。

输出选择的点的最小数量。

位于区间端点上的点也算作区间内。

输入格式：

第一行包含整数 $N$，表示区间数。

接下来 $N$ 行，每行包含两个整数 $a_i,b_i$，表示一个区间的两个端点。

输出格式：
输出一个整数，表示所需的点的最小数量。

数据范围：
$1\le N\le 10^5$
$-10^9\le a_i\le b_i\le 10^9$

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

实现思路

以右端点排序（全凭感觉），因为右端点更容易被后面的区间覆盖，而所有被这个点覆盖的区间不用再考虑。而在其之后出现的第一个没有覆盖的区间，又回到之前的问题，这个区间一定要被点覆盖，而最优点在右端点处。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include

using namespace std;

const int N = 1e5 + 10;
int main()
{
	vector<vector<int>> nums;
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int l, r;
		cin >> l >> r;
		nums.push_back({ l, r });
	}
	sort(nums.begin(), nums.end(),
		[](vector<int>& a, vector<int>& b) {return a[1] < b[1]; });
	int res = 0, ed = -2e9;
	for (auto e : nums)
	{
		if (ed >= e[0]) continue; // 非断点无需更新
		res++;
		ed = e[1];
	}
	cout << res << endl;
	return 0;
}

最大不相交区间数量

题目描述：
给定 $N$ 个闭区间 $[a_i,b_i]$，请你在数轴上选择若干区间，使得选中的区间之间互不相交（包括端点）。

输出可选取区间的最大数量。

输入格式：
第一行包含整数 $N$，表示区间数。

接下来 $N$ 行，每行包含两个整数 $a_i,b_i$，表示一个区间的两个端点。

输出格式：
输出一个整数，表示可选取区间的最大数量。

数据范围：
$1\le N\le 10^5$
$-10^9\le a_i\le b_i\le 10^9$

输入样例：

4
1 3
2 6
5 7
9 10

输出样例：

3

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include

using namespace std;

int main()
{
	int n, cnt = 0;
	cin >> n;
	vector<vector<int>> nums;
	for (int i = 0; i < n; ++i)
	{
		int l, r;
		cin >> l >> r;
		nums.push_back({l, r});
	}
	sort(nums.begin(), nums.end(),
		[](const vector<int>& a, const vector<int>& b) {return a[1] < b[1]; });
	int ed = -2e9;
	for (auto e : nums)
	{
		if (ed < e[0])
		{
			ed = e[1];
			cnt++;
		}
	}
	cout << cnt << endl;
	return 0;
}

区间分组

题目描述：
给定 $N$ 个闭区间 $[a_i,b_i]$，请你将这些区间分成若干组，使得每组内部的区间两两之间（包括端点）没有交集，并使得 组数尽可能小。

输出最小组数。

输入格式：
第一行包含整数 $N$，表示区间数。

接下来 $N$ 行，每行包含两个整数 $a_i,b_i$，表示一个区间的两个端点。

输出格式：
输出一个整数，表示最小组数。

数据范围：
$1\le N\le 10^5$
$-10^9\le a_i\le b_i\le 10^9$

输入样例：

3
-1 1
2 4
3 5

输出样例：

2

实现思路

首先按照按左端点进行排序。

使用小根堆的数据结构存储区间的右端点。

若当前遍历到的区间左端点大于等于当前小根堆所储存的最小的右端点，即可视为可以加入为统一分组，此时去除当前小根堆所储存的最小的右端点，并将目标区间的右端点加入小根堆中，视为更新了当前分组的右端点的范围。

若当前遍历到的区间左端点小于当前小根堆所储存的最小的右端点，即视为现存所有分组不满足加入该目标区间的条件，即要新开一个分组来存储当前的区间，此时直接加入目标区间的右端点，不去除小根堆的其他数据。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
#include

using namespace std;

int main()
{
	vector<vector<int>> nums;
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int l, r;
		cin >> l >> r;
		nums.push_back({l, r});
	}
	sort(nums.begin(), nums.end());
	priority_queue<int, vector<int>, greater<int>> heap;
	
	for (auto& e : nums)
	{
		if (heap.empty() || heap.top() > e[0])	heap.push(e[1]);
		else
		{
			heap.pop();
			heap.push(e[1]);
		}
	}
	cout << heap.size() << endl;
	return 0;
}

扩展：Dilworth定理

Dilworth定理：最小不相交分组数等于最大相交组的元素个数

运用定理可以把最小区间分组个数问题转化为求最大相交组的元素个数问题。（即求取最大区间厚度）

最大区间厚度的思考方法：

求 最大区间厚度 的问题，可以把这个问题想象成活动安排问题。

有若干个活动，第 $i$ 个活动开始时间和结束时间是 $[Si,Ei]$，同一个教室安排的活动之间不能交叠，求要安排所有活动，至少需要几个教室？

有时间冲突的活动不能安排在同一间教室，与该问题的限制条件相同，最小需要的教室个数即为答案。

解法：
把所有开始时间和结束时间排序，遇到开始时间就把需要的教室加 $1$，遇到结束时间就把需要的教室减 $1$，在一系列需要的教室个数变化的过程中，峰值就是多同时进行的活动数，也是我们至少需要的教室数。

代码实现

通过 左端点 × 2 与 右端点 × 2 + 1 将整个区间信息存储在一个数组当中，然后再对整个数组进行排序，而后对整个数组进行遍历。如果碰到偶数，即一个区间的左端点，代表一个活动的开始。如果碰到奇数，即一个区间的右端点，代表一个活动的结束。

注意：若是存在交点情况，即$[1,3]$$[3,9]$，由于右端点被分配为奇数，所以默认比左端点大，因此会被视为一种冲突情况，即两区间相交。

#define _CRT_SECURE_NO_WARNINGS
#include
#include
using namespace std;

const int N = 100010;
int b[2 * N], idx;

int main()
{
	int n, res = 0;
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int l, r;
		cin >> l >> r;
		b[idx++] = l * 2;
		b[idx++] = r * 2 + 1;
	}

	sort(b, b + idx);
	for (int i = 0, t = 0; i < idx; ++i)
	{
		// 出现左的个数减去右的个数差便为冲突时刻
		if (b[i] % 2 == 0) t++;
		else t--;
		res = max(res, t); // 记录冲突最多的时刻
	}
	cout << res << endl;

	return 0;
}

接受交点情况

上面的代码是不允许存在任何两个结点开始与结束在同一个点的，比如$[1,3]$和$[3,9]$，算冲突。如果能区间端点能重合的话，端点标记的 奇数偶数 就需要进行颠倒处理。

#define _CRT_SECURE_NO_WARNINGS
#include
#include
using namespace std;

const int N = 100010;
int b[2 * N], idx;

int main()
{
	int n, res = 0;
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int l, r;
		cin >> l >> r;
		// 奇数偶数颠倒处理
		b[idx++] = l * 2 + 1;
		b[idx++] = r * 2;
	}

	sort(b, b + idx);
	for (int i = 0, t = 0; i < idx; ++i)
	{
		// 出现左的个数减去右的个数差便为冲突时刻
		if (b[i] % 2) t++;
		else t--;
		res = max(res, t); // 记录冲突最多的时刻
	}
	cout << res << endl;

	return 0;
}

区间覆盖

题目描述：
给定 $N$ 个闭区间 $[a_i,b_i]$ 以及一个线段区间 $[s,t]$，请你 选择尽量少的区间，将指定线段区间完全覆盖。

输出最少区间数，如果无法完全覆盖则输出 −1。

输入格式：
第一行包含两个整数 $s$ 和 $t$，表示给定线段区间的两个端点。

第二行包含整数 $N$，表示给定区间数。

接下来 $N$ 行，每行包含两个整数 $a_i,b_i$，表示一个区间的两个端点。

输出格式：
输出一个整数，表示所需最少区间数。

如果无解，则输出 −1。

数据范围：
$1\le N\le 10^5$

$-10^9\le a_i\le b_i\le 10^9$

$-10^9\le s\le t\le 10^9$

输入样例：

1 5
3
-1 3
2 4
3 5

输出样例：

2

实现思路思路

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
using namespace std;

int main()
{
	vector<vector<int>> nums;
	int n, st, ed, res = 0;
	cin >> st >> ed >> n;
	for (int i = 0; i < n; ++i)
	{
		int l, r;
		cin >> l >> r;
		nums.push_back({l, r});
	}
	sort(nums.begin(), nums.end());
	bool success = false;
	for (int i = 0; i < n; ++i)
	{
		int j = i, r = -2e9;
		while (j < n && nums[j][0] <= st)
		{
			r = max(r, nums[j][1]);
			j++;
		}
		if (r < st)
		{
			res = -1;
			break;
		}
		res++;
		if (r >= ed)
		{
			success = true;
			break;
		}
		st = r;
		i = j - 1;
	}
	if (!success) res = -1;
	cout << res << endl;
	return 0;
}

Huffman树

合并果子

题目描述：
在一个果园里，达达已经将所有的果子打了下来，而且按果子的不同种类分成了不同的堆。

达达决定把所有的果子合成一堆。

每一次合并，达达可以把两堆果子合并到一起，消耗的体力等于两堆果子的重量之和。

可以看出，所有的果子经过 $n-1$ 次合并之后，就只剩下一堆了。

达达在合并果子时总共消耗的体力等于每次合并所耗体力之和。

因为还要花大力气把这些果子搬回家，所以达达在合并果子时要尽可能地节省体力。

假定每个果子重量都为 $1$，并且已知果子的种类数和每种果子的数目，你的任务是设计出合并的次序方案，使达达耗费的体力最少，并输出这个最小的体力耗费值。

例如有 $3$ 种果子，数目依次为 $1，2，9$。

可以先将 $1、2$ 堆合并，新堆数目为 $3$，耗费体力为 $3$。

接着，将新堆与原先的第三堆合并，又得到新的堆，数目为 $12$，耗费体力为 $12$。

所以 $达达总共耗费体力=3+12=15$。

可以证明 $15$ 为最小的体力耗费值。

输入格式：
输入包括两行，第一行是一个整数 $n$，表示果子的种类数。

第二行包含 $n$ 个整数，用空格分隔，第 $i$ 个整数 $a_i$ 是第 $i$ 种果子的数目。

输出格式：
输出包括一行，这一行只包含一个整数，也就是最小的体力耗费值。

输入数据保证这个值小于 $2^{31}$。

数据范围：
$1\le n\le 10000$
$1\le a_i\le 20000$

输入样例：

3 
1 2 9 

输出样例：

15

算法思路

与区间DP中石子合并的问题很相似，但是石子合并只能 每次只能合并相邻的两堆 导致不能用本题的方法进行求解。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include
#include
using namespace std;

int main()
{
	int n, res = 0;
	cin >> n;
	priority_queue<int, vector<int>, greater<int>> heap;
	while (n--)
	{
		int x;
		cin >> x;
		heap.push(x);
	}
	while (heap.size() != 1)
	{
		int a = heap.top();
		heap.pop();
		int b = heap.top();
		heap.pop();
		res += (a + b);
		heap.push(a + b);
	}
	cout << res << endl;
	return 0;
}

排序不等式

排队打水

题目描述：
有 $n$ 个人排队到 $1$ 个水龙头处打水，第 $i$ 个人装满水桶所需的时间是 $t_i$，请问如何安排他们的打水顺序才能使所有人的等待时间之和最小？

输入格式：
第一行包含整数 $n$。

第二行包含 $n$ 个整数，其中第 $i$ 个整数表示第 $i$ 个人装满水桶所花费的时间 $t_i$。

输出格式：
输出一个整数，表示最小的等待时间之和。

数据范围：
$1\le n\le 10^5$
$1\le t_i\le 10^4$

输入样例：

7
3 6 1 4 2 5 7

输出样例：

56

算法思路

$$sum=\sum _{i=1}^n(n-i+1)\ast a[i]$$

因此每回选择耗时最短的人去打水

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include
using namespace std;

const int N = 100010;
int a[N];

int main()
{
	int n;
	long long res = 0;
	cin >> n;
	for (int i = 0; i < n; ++i) cin >> a[i];
	sort(a, a + n);
	for (int i = 0; i < n; ++i) res += (long long)a[i] * (n - i - 1);
	cout << res << endl;
	return 0;
}

绝对值不等式

货仓选址

题目描述：
在一条数轴上有 $N$ 家商店，它们的坐标分别为 $A_1\sim A_N$。

现在需要在数轴上建立一家货仓，每天清晨，从货仓到每家商店都要运送一车商品。

为了提高效率，求把货仓建在何处，可以使得 货仓到每家商店的距离之和最小。

输入格式：
第一行输入整数 $N$。

第二行 $N$ 个整数 $A_1\sim A_N$。

输出格式：
输出一个整数，表示距离之和的最小值。

数据范围：
$1\le N\le 100000,0\le A_i\le 40000$

输入样例：

4
6 2 9 1

输出样例：

12

算法思路

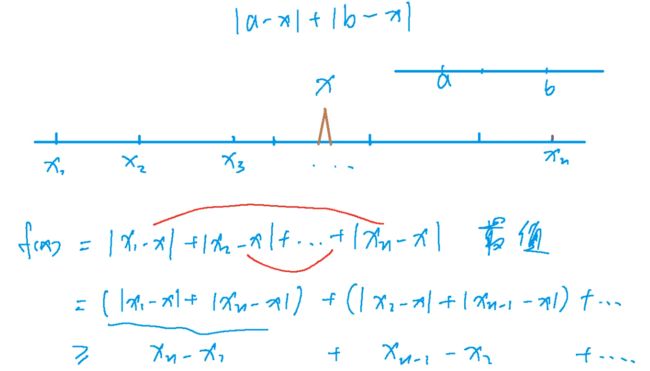
将绝对值函数里的，项数进行重新排列，让如 $|x_1-x|+|x_n-x|$ 凑为一项，当 $x$ 处于 $x_1$ 与 $x_n$ 之间时，$x$ 到 $x_1$ 与 $x_n$ 的距离最小，以此类推当 $x$ 处于整个大区间的中间时候，$x$ 到各点的距离最短。

代码实现

#define _CRT_SECURE_NO_WARNINGS
#include
#include
using namespace std;

const int N = 100010;
int a[N];

int main()
{
	int n, ans = 0;
	cin >> n;
	for (int i = 0; i < n; ++i) cin >> a[i];
	sort(a, a + n);
	for (int i = 0; i < n; ++i) ans += abs(a[i] - a[n / 2]);
	cout << ans << endl;
	return 0;
}

推公式

国王游戏

题目描述：

恰逢 H 国国庆，国王邀请 $n$ 位大臣来玩一个有奖游戏。首先，他让每个大臣在左、右手上面分别写下一个整数，国王自己也在左、右手上各写一个整数。然后，让这 $n$ 位大臣排成一排，国王站在队伍的最前面。排好队后，所有的大臣都会获得国王奖赏的若干金币，每位大臣获得的金币数分别是：排在该大臣前面的所有人的左手上的数的乘积除以他自己右手上的数，然后向下取整得到的结果。

国王不希望某一个大臣获得特别多的奖赏，所以他想请你帮他重新安排一下队伍的顺序，使得获得奖赏最多的大臣，所获奖赏尽可能的少。注意，国王的位置始终在队伍的最前面。

输入格式：

第一行包含一个整数 $n$，表示大臣的人数。

第二行包含两个整数 $a$ 和 $b$，之间用一个空格隔开，分别表示国王左手和右手上的整数。

接下来 $n$ 行，每行包含两个整数 $a$ 和 $b$，之间用一个空格隔开，分别表示每个大臣左手和右手上的整数。

输出格式：

一个整数，表示重新排列后的队伍中获奖赏最多的大臣所获得的金币数。

数据范围：

对于 $20\%$ 的数据，有 $1\le n\le 100<a,b<8$；

对于 $40\%$ 的数据，有 $1\le n\le 200<a,b<8$；

对于 $60\%$ 的数据，有 $1\le n\le 100$；

对于 $60\%$ 的数据，保证答案不超过 $10^9$；

对于 $100\%$ 的数据，有 $1\le n\le 10000<a,b<10000$。

输入样例：

3 
1 1 
2 3 
7 4 
4 6

输出样例：

2

【输入输出样例说明】

按 $1$、$2$、$3$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按 $1$、$3$、$2$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按 $2$、$1$、$3$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按 $2$、$3$、$1$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $9$；

按 $3$、$1$、$2$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $2$；

按 $3$、$2$、$1$ 这样排列队伍，获得奖赏最多的大臣所获得金币数为 $9$。

因此，奖赏最多的大臣最少获得 $2$ 个金币，答案输出 $2$。

算法思路

考虑两个大臣 $p_1,p_2$，他们站在国王 $p_0$ 身后，这时候可以分为两种情况：
​
情况一：

人物	左手	右手
$p_0$	$a_0$	$b_0$
$p_1$	$a_1$	$b_1$
$p_2$	$a_2$	$b_2$

情况二：

人物	左手	右手
$p_0$	$a_0$	$b_0$
$p_2$	$a_2$	$b_2$
$p_1$	$a_1$	$b_1$

对于情况一：
$an{s}_1=max(\frac{a_0}{b_1},\frac{a_0\ast a_1}{b_2})$

对于情况二：
$an{s}_2=max(\frac{a_0}{b_2},\frac{a_0\ast a_2}{b_1})$

可以发现 $\frac{a_0\ast a_2}{b_1}>\frac{a_0}{b_1}$ 和 $\frac{a_0\ast a_1}{b_2}>\frac{a_0}{b_2}$，因此如果要使 $an{s}_2>an{s}_1$ ，要让 $\frac{a_0\ast a_2}{b_1}>\frac{a_0\ast a_1}{b_2}$。即让 $a_0\ast a_2\ast b_2>a_0\ast a_1\ast b_1$，也就是 $a_2\ast b_2>a_1\ast b_1$。

因此可以得出结论，$a_i\ast b_i>a_j\ast b_j$ 可以得出 $an{s}_i>an{s}_j$。为了使 $ans$ 更小，需要将 $a_i\ast b_i$ 较小的放在前面，我们以 $a_i\ast b_i$ 为关键字排序即可。

代码实现

无高精度计算版本：

#define _CRT_SECURE_NO_WARNINGS
#include
#include
using namespace std;

int main()
{
	vector<vector<int>> persons;
	int n;
	cin >> n;
	for (int i = 0; i <= n; ++i)
	{
		int l, r;
		cin >> l >> r;
		persons.push_back({l, r});
	}
	// 注意国王不参与排序
	sort(persons.begin() + 1, persons.end(),
		[](const vector<int>& a, const vector<int>& b){return a[0] * a[1] < b[0] * b[1]; });
	long long cnt = persons[0][0], res = 0;
	for (int i = 1; i <= n; ++i)
	{
		res = max(res, cnt / persons[i][1]);
		cnt *= persons[i][0];
	}
	cout << res << endl;
	return 0;
}

高精度计算版本：

#define _CRT_SECURE_NO_WARNINGS

#include
#include
#include
using namespace std;

vector<int> hp_mul(vector<int> lhs, int l) // 高精度乘法
{
	vector<int> res;
	for (int i = 0, t = 0; i < lhs.size() || t; ++i)
	{
		if (i < lhs.size()) t += lhs[i] * l;
		res.push_back(t % 10);
		t /= 10;
	}
	return res;
}
vector<int> hp_div(vector<int> lhs, int r) // 高精度除法
{
	vector<int> res;
	for (int i = lhs.size() - 1, t = 0; i >= 0; --i)
	{
		t = lhs[i] + t * 10;
		res.push_back(t / r);
		t %= r;
	}
	return res;
}
long long get_num(vector<int> num) //  从数组提取出数字
{
	long long res = 0;
	for (int i = num.size() - 1; i >= 0; --i)
		res = res * 10 + num[i];
	return res;
}
int main()
{
	vector<vector<int>> nums;
	int n;
	cin >> n;
	for (int i = 0; i <= n; ++i)
	{
		int l, r;
		cin >> l >> r;
		nums.push_back({l, r});
	}
	sort(nums.begin() + 1, nums.end(), [](const vector<int>& a, const vector<int>& b)
		{return a[0] * a[1] < b[0] * b[1]; });
	long long ans = 0;
	vector<int> lcj;
	int t = nums[0][0];
	while (t)
	{
		lcj.push_back(t % 10);
		t /= 10;
	}
	for (int i = 1; i <= n; ++i)
	{
		ans += get_num(hp_div(lcj, nums[i][1]));
		lcj = hp_mul(lcj, nums[i][0]);
	}
	cout << ans << endl;
	return 0;
}

耍杂技的牛

题目描述：
农民约翰的 $N$ 头奶牛（编号为 $\mathrm{1..}N$）计划逃跑并加入马戏团，为此它们决定练习表演杂技。

奶牛们不是非常有创意，只提出了一个杂技表演：

叠罗汉，表演时，奶牛们站在彼此的身上，形成一个高高的垂直堆叠。

奶牛们正在试图找到自己在这个堆叠中应该所处的位置顺序。

这 $N$ 头奶牛中的每一头都有着自己的重量 $W_i$ 以及自己的强壮程度 $S_i$。

一头牛支撑不住的可能性取决于它头上所有牛的总重量（不包括它自己）减去它的身体强壮程度的值，现在称该数值为 风险值，风险值越大，这只牛撑不住的可能性越高。

您的任务是 确定奶牛的排序，使得所有奶牛的风险值中的 最大值 尽可能的小。

输入格式：
第一行输入整数 $N$，表示奶牛数量。

接下来 $N$ 行，每行输入两个整数，表示牛的重量和强壮程度，第 $i$ 行表示第 $i$ 头牛的重量 $W_i$ 以及它的强壮程度 $S_i$。

输出格式：
输出一个整数，表示最大风险值的最小可能值。

数据范围：
$1\le N\le 50000$
$1\le W_i\le 10000$
$1\le S_i\le 10^9$

输入样例：

3
10 3
2 5
3 3

输出样例：

2

算法思路

考虑三头牛的情况 $n_1,n_2,n_3$，$n_1$在最上面，假设 $n_1$ 牛不改变仅改变 $n_2$和$n_3$牛，这时候可以分为两种情况：
​
情况一：

牛	重量	强壮程度
$n_1$	$n_1$	$n_1$
$n_1$	$n_1$	$n_1$
$n_2$	$n_2$	$n_2$

情况二：

牛	重量	强壮程度
$n_1$	$n_1$	$n_1$
$n_3$	$n_3$	$n_3$
$n_2$	$n_2$	$n_2$

可以推出：
对于情况一：
$an{s}_1=max(w_1-s_2,w_1+w_2-s_3)$

对于情况二：
$an{s}_2=max(w_1-s_3,w_1+w_3-s_2)$

易得，$w_1+w_2-s_3>w_1-s_3$ 和 $w_1+w_3-s_2>w_1-s_2$，因此假设要判断 $an{s}_1>an{s}_2$，只需判断 $w_1+w_2-s_3>w_1+w_3-s_2$，即 $w_2+s_2>w_3+s_3$。所以要使 $an{s}_i$ 尽可能将较小的 $w_i+s_i$ 放到上面的位置。

代码实现

#define _CRT_SECURE_NO_WARNINGS

#include
#include
#include
using namespace std;

int main()
{
	vector<vector<int>> nums;
	int n;
	cin >> n;
	for (int i = 0; i < n; ++i)
	{
		int w, s;
		cin >> w >> s;
		nums.push_back({w, s});
	}
	sort(nums.begin(), nums.end(), [](const vector<int>& a, const vector<int>& b)
		{return a[0] + a[1] < b[0] + b[1]; });
	int sum = nums[0][0], ans = nums[0][0] - nums[1][1];
	for (int i = 1; i < n; ++i)
	{
		ans = max(ans, sum - nums[i][1]);
		sum += nums[i][0];
	}
	cout << ans << endl;
	return 0;
}