(图论) ——【Leetcode每日一题】

❓ 1020. 飞地的数量

难度：中等

给你一个大小为 m x n 的二进制矩阵 grid ，其中 0 表示一个 海洋单元格、1 表示一个 陆地单元格。

一次 移动 是指从一个陆地单元格走到另一个相邻（上、下、左、右）的陆地单元格或跨过 grid 的边界。

返回网格中 无法 在任意次数的移动中离开网格边界的陆地单元格的数量。

示例 1：

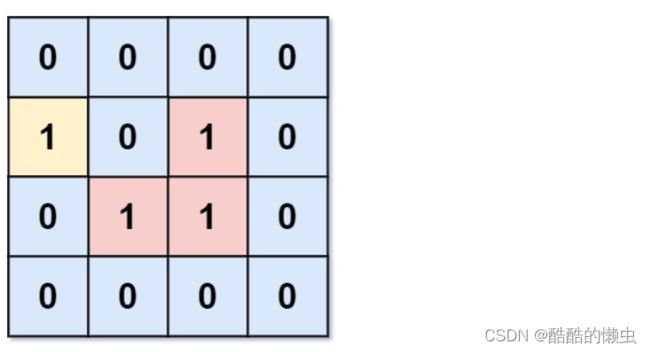
输入：grid = [[0,0,0,0],[1,0,1,0],[0,1,1,0],[0,0,0,0]]
输出：3
解释：有三个 1 被 0 包围。一个 1 没有被包围，因为它在边界上。

示例 2：

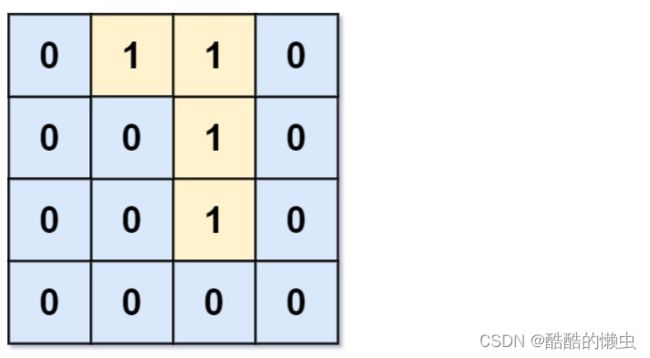
输入：grid = [[0,1,1,0],[0,0,1,0],[0,0,1,0],[0,0,0,0]]
输出：0
解释：所有 1 都在边界上或可以到达边界。

提示：

• m == grid.length
• n == grid[i].length
• 1 <= m, n <= 500
• grid[i][j] 的值为 0 或 1

思路：DFS

本题要求找到不靠边的陆地面积，那么

• 我们只要从周边找到陆地
• 然后 通过 dfs 或者 bfs 将周边靠陆地且相邻的陆地都变成海洋，
• 然后再去重新遍历地图的时候，统计此时还剩下的陆地就可以了。

代码：(C++、Java)

C++

class Solution {
private:
    int dir[4][2] = {-1, 0, 0, -1, 1, 0, 0, 1}; // 保存四个方向
    int m = 0, n = 0;
    void dfs(int i, int j, vector<vector<int>>& grid){
        if(grid[i][j] == 0){ // 是海洋则返回
            return;
        }
        grid[i][j] = 0;
        for(int k = 0; k < 4; k++){ // 向四个方向遍历
            int nexti = i + dir[k][0];
            int nextj = j + dir[k][1];
            if(nexti < 0 || nexti >= m || nextj < 0 || nextj >= n) continue;
            dfs(nexti, nextj, grid);
        }
    }
public:
    int numEnclaves(vector<vector<int>>& grid) {
        m = grid.size();
        n = grid[0].size();
        // 从左侧边，和右侧边 向中间遍历
        for(int i = 0; i < m; i++){
            dfs(i, 0, grid);
            dfs(i, n - 1, grid);
        }
        // 从上边和下边 向中间遍历
        for(int i = 0; i < n; i++){
            dfs(0, i, grid);
            dfs(m - 1, i, grid);
        }
        //统计剩余陆地的面积
        int ans = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1) ans++;
            }
        }
        return ans;
    }
};

Java

class Solution {
    private int[][] dir = {{-1, 0}, {0, -1}, {1, 0}, {0, 1}}; // 四个方向
    int m = 0, n = 0;

    private void dfs(int i, int j, int[][] grid){
        if(grid[i][j] == 0) return;// 是海洋则返回
        grid[i][j] = 0;
        for(int k = 0; k < 4; k++){// 向四个方向遍历
            int nexti = i + dir[k][0];
            int nextj = j + dir[k][1];
            // 超过边界
            if(nexti < 0 || nexti >= m || nextj < 0 || nextj >= n) continue;
            dfs(nexti, nextj, grid);
        }
    }
    public int numEnclaves(int[][] grid) {
        m = grid.length;
        n = grid[0].length;
        // 从左侧边，和右侧边 向中间遍历
        for(int i = 0; i < m; i++){
            dfs(i, 0, grid);
            dfs(i, n - 1, grid);
        }
        // 从上边和下边 向中间遍历
        for(int j = 0; j < n; j++){
            dfs(0, j, grid);
            dfs(m - 1, j, grid);
        }
        //统计剩余陆地的面积
        int ans = 0;
        for(int i = 0; i < m; i++){
            for(int j = 0; j < n; j++){
                if(grid[i][j] == 1) ans++;
            }
        }
        return ans;
    }
}

运行结果：

复杂度分析：

• 时间复杂度：$O(mn)$，其中m 和 n 分别是网格 grid 的行数和列数。深度优先搜索最多访问每个单元格一次，需要 $O(mn)$ 的时间，遍历网格统计飞地的数量也需要 $O(mn)$ 的时间。

• 空间复杂度：$O(mn)$，空间复杂度主要取决于递归调用栈空间，最大空间复杂度是 $O(mn)$。

题目来源：力扣。

放弃一件事很容易，每天能坚持一件事一定很酷，一起每日一题吧！
关注我LeetCode主页 / CSDN—力扣专栏，每日更新！

注： 如有不足，欢迎指正！