什么是树?什么是B树?B-树?B+树?B*树?红黑树?平衡搜索树?
1、树:没有父节点的节点称为根节点,每个节点都有零个或多个子节点。
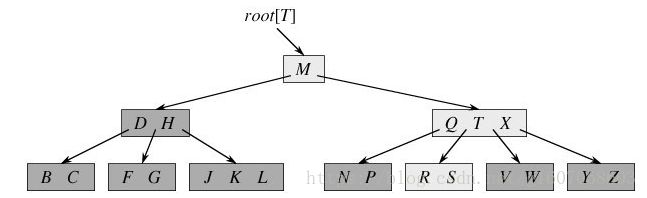
2、B树(B-):多路查找树(不是二叉的),是满足某些特性的m叉树。
B树是为实现高效的磁盘存取而设计的多叉平衡搜索树。
B树产生的原因:B树是一种查找树,它最初启发于二叉查找树,二叉查找树的特点是每个非叶子节点都只有两个孩子节点。然而这种做法会导致数据量非常大时,二叉查找树的深度过深,搜索算法自根节点向下搜索时,需要访问的节点也就变得相当多。如果这些节点存储在外存储器中,每访问一个节点,相当于就是进行了一次IO操作,随着树高度的增加,频繁的IO操作一定会降低查询的效率。
这里有一个基本的概念,就是说我们从外存储器中读取信息的步骤,简单来分,大致有两步:
第一:找到存储这个数据所对应的磁盘页面,这个过程是机械化的过程,需要依靠磁臂的转动,找到对应的磁道,所以耗时长。
第二:读取数据进内存,并实施运算,这是电子化的过程,相当快。
综上,对于外存储器的信息读取最大的信息消耗在于寻找磁盘页面。那么一个基本的想法就是能不能减少这种读取的次数,在一个磁盘页面上,多存储一些索引信息。B树的基本逻辑就是这个思路,它要改二叉为多叉,每个节点存储更多的指针信息,以降低I/O操作。
特性:
(1) 树中每个节点至多有m棵子树。
(2) 若根节点不是叶子节点,则至少有两棵子树。
(3) 除根之外的所有非终端节点至少有m/2(向上取整)棵子树。
(4) 所有的非终端节点中都包含关键字信息和指向子节点的指针。
(5) 所有叶子节点出现在同一层次上,叶子节点不带信息。
(6) 非叶子结点的关键字个数= 指向儿子的指针个数-1;
(7) 非叶子结点的关键字:K[1], K[2], …, K[M-1];且K[i] < K[i+1];
(8) 非叶子结点的指针:P[1], P[2], …, P[M];其中P[1]指向关键字小于K[1]的子树,P[M]指向关键字大于K[M-1]的子树,其它P[i]指向关键字属于(K[i-1], K[i])的子树;
B树的优点:
当你要查找的值处于非叶子节点时,当到该非叶子节点时,查找就成功的结束了;而B+树,非叶子节点只是索引部分,需要一直查找到叶子节点。
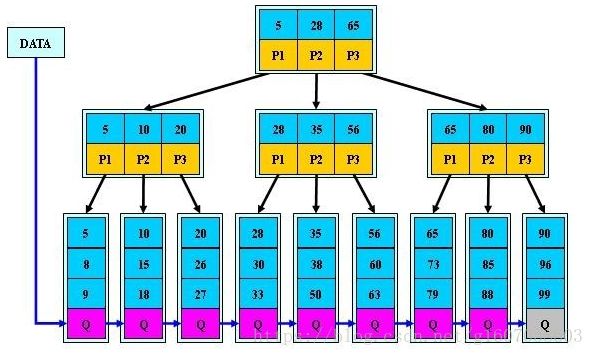
3、B+树
(1)其基本定义和B-树相同。
(2)非叶子节点的儿子数=关键字个数。
(3)非叶子结点的子树指针P[i],指向关键字值属于[K[i], K[i+1])的子树
(B-树是开区间);
(4)全部的关键字都出现在叶子节点,且叶子节点本身依赖于关键字的大小顺序排序。
注:B树和B+树的区别?
(1)结构上
B树中指向文件的关键字集合分布在整棵树中,叶节点中不包含任何关键字信息,而B+树中所有指向文件的关键字及其指针集合分布在叶子节点上,非叶子节点的关键字只是叶子节点关键字的索引,即内部节点仅仅起到索引的作用。
B树中任何一个关键字只出现在一个节点中,而B+树中的关键字必须出现在叶子节点中,也可能在非叶子节点中重复出现。
(2)性能上(也即为什么说B+树比B树更适合实际应用中操作系统的文件索引和数据库索引?)
B+树的磁盘读写代价更低。B+树的内部节点并没有指向关键字具体信息的指针,其内部节点比B树小,盘块能容纳的节点中关键字数量更多,一次性读入内存中可以查找的关键字也就越多,相对的,IO读写次数也就降低了。而IO读写次数是影响索引检索效率最大的因素。
B+树的查询效率更加稳定。B树搜索有可能会在非叶子节点结束,越靠近根节点的记录查找时间越短,只要找到关键字即可确定记录的存在,其性能等价于在关键字全集内做一次二分查找。而在B+树中,任何关键字的查找都必须走一条从根节点到叶节点的路,所有关键字的查找路径长度相同,导致每一个关键字的查询效率相当。
B树在提高了磁盘IO性能的同时并没有解决元素遍历的效率低下的问题。B+树的叶子节点使用指针顺序连接在一起,只要遍历叶子节点就可以实现整棵树的遍历,即解决对全部关键字信息的扫描。而且,在数据库中基于范围的查询是非常频繁的,而B树不支持这样的操作(或者说效率太低)。
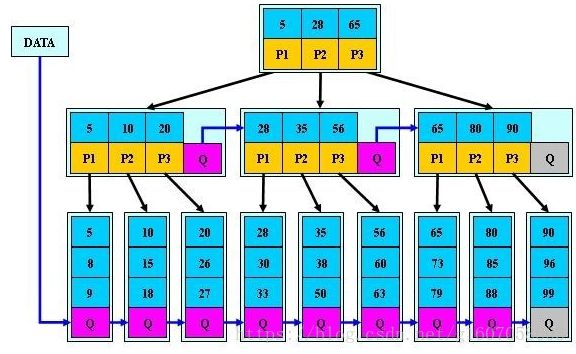
4、B*树
(1)是B+树的变体,在B+树的非根和非叶子节点,再增加指向兄弟的指针。
(2)B*树中非叶子节点的关键字个数>=2m/3,即块的最低使用率为2/3;(B+树为1/2);
注:B+树比B树更适合文件系统索引和数据库索引。
B-树:有序数组+平衡多叉树
B+树:有序数组链表+平衡多叉树
B*树:一个丰满的B+树
5、红黑树
红黑树本质上是一种二叉查找树,但它在二叉查找树的基础上额外添加了一个标记(颜色),同时具有一定的规则。这些规则使红黑树保证了一种平衡,插入、删除、查找的最坏时间复杂度都为 O(logn)。
- 每个节点要么是红色,要么是黑色;
- 根节点永远是黑色的;
- 所有的叶节点都是是黑色的(注意这里说叶子节点其实是上图中的 NIL 节点);
- 每个红色节点的两个子节点一定都是黑色;
- 从任一节点到其子树中每个叶子节点的路径都包含相同数量的黑色节点。
注意:
性质 3 中指定红黑树的每个叶子节点都是空节点,而且叶子节点都是黑色。但 Java 实现的红黑树将使用 null 来代表空节点,因此遍历红黑树时将看不到黑色的叶子节点,反而看到每个叶子节点都是红色的。
性质 4 的意思是:从每个根到节点的路径上不会有两个连续的红色节点,但黑色节点是可以连续的。
因此若给定黑色节点的个数 N,最短路径的情况是连续的 N 个黑色,树的高度为 N - 1;最长路径的情况为节点红黑相间,树的高度为 2(N - 1) 。
性质 5 是成为红黑树最主要的条件,后序的插入、删除操作都是为了遵守这个规定。
红黑树并不是标准平衡二叉树,它以性质 5 作为一种平衡方法,使自己的性能得到了提升。
6、平衡搜索树(ALV)
AVL树是一种高度平衡的二叉搜索树,它的每个结点都有一个平衡因子,这个平衡因子的取值是-1,0,1(平衡因子 = 右子树高度 - 左子树高度)
AVL树具有的性质:
1.左子树和右子树的高度差不超过1;
2.树中的各子树都是AVL树.