数据结构和算法（6）：图

概述

图
所谓的图，可定义为 $G=(V,E)$。其中，集合 $V$ 中的元素称作顶点。集合 $E$ 中的元素分别对应于 $V$ 中的
某一对顶点 $(u,v)$，表示它们之间存在某种关系，故亦称作边。在某些文献中，顶点也称作节点，边亦称作弧。

从计算的需求出发，约定 $V$ 和 $E$ 均为有限集，通常将其规模分别记 $n=|V|$ 和 $e=|E|$。
若边 $(u,v)$ 所对应顶点 $u$ 和 $v$ 的次序无所谓，则称作无向边。反之若 $u$ 和 $v$ 不对等，则称 $(u,v)$ 为有向边。无向边 $(u,v)$ 可记作 $(v,u)$，而有向的 $(u,v)$ 和 $(v,u)$ 则不可混淆。
有向边 $(u,v)$ 从 $u$ 指向 $v$，其中 $u$ 称作该边的起点或尾顶点，而 $v$ 称作该边的终点或头顶点。

若 $E$ 中各边均无方向，则 $G$ 称作无向图；反之，若 $E$ 中只含有向边，则 $G$ 称作有向图；若 $E$ 同时包含无向边和有向边，则 $G$ 称作混合图。

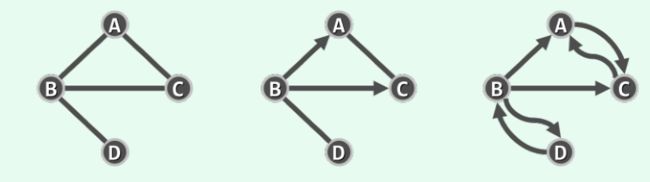
无向图和混合图都可转化为有向图。

联接于同一顶点之间的边，称作自环。不含任何自环的图称作简单图。

度
对于任何边 $e=(u,v)$，称顶点 $u$ 和 $v$ 彼此邻接，互为邻居；而它们都与边 $e$ 彼此关联。在无向图中，与顶点 $v$ 关联的边数，称作 $v$ 的度数（degree），记作deg(v)。

对于有向边 $e=(u,v)$，$e$ 称作 $u$ 的出边、$v$ 的入边。$v$ 的出边总数称作其出度，记作outdeg(v)；入边总数称作其入度，记作indeg(v)。
上面的图中：
第一个图：顶点{ A, B, C, D }的度数为{ 2, 3, 2, 1 }
第三个图：顶点{ A, B, C, D }的出度为{ 1, 3, 1, 1 }，入度为{ 2, 1, 2, 1 }。

通路与环路
所谓路径或通路，就是由 $m+1$ 个顶点与 $m$ 条边交替而成的一个序列：$\pi =\{v_0,e_1,v_1,e_2,v_2,...,e_m,v_m\}$。且对任何 $0<i\le m$ 都有 $e_i=(v_{i-1},v_i)$。也就是说，这些边依次地首尾相联。其中沿途边的总数 $m$，亦称作通路的长度，记作 $|\pi |=m$。

沿途顶点互异的通路，称作简单通路

完全图是一种特殊的图，其中任何两个顶点之间都有一条边。完全图的顶点数为n的图记作 $K_n$。
如果一个图的所有顶点都在一个平面上，那么它是平面图。换句话说，如果一个图可以被画在平面上，使得所有的边只在交叉点相交，那么这个图就是平面图。
对于完全图 $K_n$，当 $n\ge 5$ 时，它一定不是平面图

库拉托夫斯基定理，一个图是平面图当且仅当它不含K5或K3,3的子图。而完全图Kn（n≥5）必然包含K5或K3,3的子图，因此它一定不是平面图。

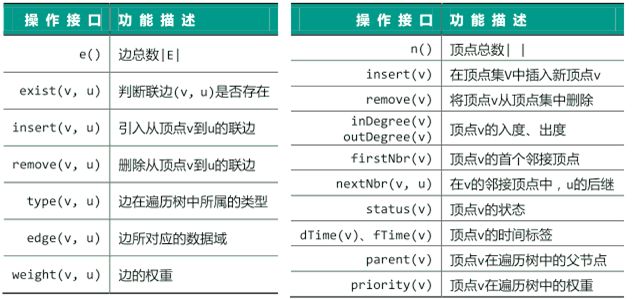
邻接矩阵

Graph 模板类

using VStatus = enum { UNDISCOVERED, DISCOVERED, VISITED }; //顶点状态
using EType = enum { UNDETERMINED, TREE, CROSS, FORWARD, BACKWARD }; //边在遍历树中所属的类型
 
template <typename Tv, typename Te> //顶点类型、边类型
class Graph { //图Graph模板类
private:
   void reset() { //所有顶点、边的辅助信息复位
      for ( Rank v = 0; v < n; v++ ) { //所有顶点的
         status( v ) = UNDISCOVERED; dTime( v ) = fTime( v ) = -1; //状态，时间标签
         parent( v ) = -1; priority( v ) = INT_MAX; //（在遍历树中的）父节点，优先级数
         for ( Rank u = 0; u < n; u++ ) //所有边的
            if ( exists( v, u ) ) type( v, u ) = UNDETERMINED; //类型
      }
   }
   void BFS( Rank, Rank& ); //（连通域）广度优先搜索算法
   void DFS( Rank, Rank& ); //（连通域）深度优先搜索算法
   void BCC( Rank, Rank&, Stack<Rank>& ); //（连通域）基于DFS的双连通分量分解算法
   bool TSort( Rank, Rank&, Stack<Tv>* ); //（连通域）基于DFS的拓扑排序算法
   template <typename PU> void PFS( Rank, PU ); //（连通域）优先级搜索框架
public:
// 顶点
   Rank n; //顶点总数
   virtual Rank insert( Tv const& ) = 0; //插入顶点，返回编号
   virtual Tv remove( Rank ) = 0; //删除顶点及其关联边，返回该顶点信息
   virtual Tv& vertex( Rank ) = 0; //顶点的数据（该顶点的确存在）
   virtual Rank inDegree( Rank ) = 0; //顶点的入度（该顶点的确存在）
   virtual Rank outDegree( Rank ) = 0; //顶点的出度（该顶点的确存在）
   virtual Rank firstNbr( Rank ) = 0; //顶点的首个邻接顶点
   virtual Rank nextNbr( Rank, Rank ) = 0; //顶点（相对当前邻居的）下一邻居
   virtual VStatus& status( Rank ) = 0; //顶点的状态
   virtual Rank& dTime( Rank ) = 0; //顶点的时间标签dTime
   virtual Rank& fTime( Rank ) = 0; //顶点的时间标签fTime
   virtual Rank& parent( Rank ) = 0; //顶点在遍历树中的父亲
   virtual int& priority( Rank ) = 0; //顶点在遍历树中的优先级数
// 边：这里约定，无向边均统一转化为方向互逆的一对有向边，从而将无向图视作有向图的特例
   Rank e; //边总数
   virtual bool exists( Rank, Rank ) = 0; //边(v, u)是否存在
   virtual void insert( Te const&, int, Rank, Rank ) = 0; //在两个顶点之间插入指定权重的边
   virtual Te remove( Rank, Rank ) = 0; //删除一对顶点之间的边，返回该边信息
   virtual EType& type( Rank, Rank ) = 0; //边的类型
   virtual Te& edge( Rank, Rank ) = 0; //边的数据（该边的确存在）
   virtual int& weight( Rank, Rank ) = 0; //边(v, u)的权重
// 算法
   void bfs( Rank ); //广度优先搜索算法
   void dfs( Rank ); //深度优先搜索算法
   void bcc( Rank ); //基于DFS的双连通分量分解算法
   Stack<Tv>* tSort( Rank ); //基于DFS的拓扑排序算法
   void prim( Rank ); //最小支撑树Prim算法
   void dijkstra( Rank ); //最短路径Dijkstra算法
   template <typename PU> void pfs( Rank, PU ); //优先级搜索框架
};

顶点和边

template <typename Tv> struct Vertex { //顶点对象（为简化起见，幵未严格封装）
	Tv data; int inDegree, outDegree; VStatus status; //数据、出入度数、状态
	int dTime, fTime; //时间标签
	int parent; int priority; //在遍历树中的父节点、优先级数
	Vertex(Tv const& d = (Tv)0) : //构造新顶点
		data(d), inDegree(0), outDegree(0), status(UNDISCOVERED),
		dTime(-1), fTime(-1), parent(-1), priority(INT_MAX) {} //暂不考虑权重溢出
};

template <typename Te> struct Edge { //边对象（为简化起见，并未严格封装）
	Te data; int weight; EType type; //数据、权重、类型
	Edge(Te const& d, int w) : data(d), weight(w), type(UNDETERMINED) {} //构造
};

template <typename Tv, typename Te> //顶点类型、边类型

邻接矩阵

邻接矩阵（adjacency matrix）是图 ADT 最基本的实现方式，使用方阵A[n][n]表示由n个顶点构成的图，其中每个单元，各自负责描述一对顶点之间可能存在的邻接关系，故此得名。

class GraphMatrix : public Graph<Tv, Te> { //基亍向量，以邻接矩阵形式实现的图
private:
	Vector< Vertex< Tv > > V; //顶点集（向量）
	Vector< Vector< Edge< Te >* > > E; //边集（邻接矩阵）
public:
	GraphMatrix() { n = e = 0; } //构造
	~GraphMatrix() { //析构
		for (int j = 0; j < n; j++) //所有动态创建的
			for (int k = 0; k < n; k++) //边记录
				delete E[j][k]; //逐条清除
	}
// 顶点的基本操作：查询第i个顶点（0 <= i < n）
	virtual Tv & vertex(int i) { return V[i].data; } //数据
	virtual int inDegree(int i) { return V[i].inDegree; } //入度
	virtual int outDegree(int i) { return V[i].outDegree; } //出度
	virtual int firstNbr(int i) { return nextNbr(i, n); } //首个邻接顶点
	virtual int nextNbr(int i, int j) //相对于顶点j的下一邻接顶点（改用邻接表可提高效率）
	{ while ((-1 < j) && (!exists(i, --j))); return j; } //逆向线性试探
	virtual VStatus & status(int i) { return V[i].status; } //状态
	virtual int& dTime(int i) { return V[i].dTime; } //时间标签dTime
	virtual int& fTime(int i) { return V[i].fTime; } //时间标签fTime
	virtual int& parent(int i) { return V[i].parent; } //在遍历树中的父亲
	virtual int& priority(int i) { return V[i].priority; } //在遍历树中的优先级数
// 顶点的动态操作
	virtual int insert(Tv const& vertex) { //插入顶点，返回编号
		for (int j = 0; j < n; j++) E[j].insert(NULL); n++; //各顶点预留一条潜在的关联边
		E.insert(Vector<Edge<Te>*>(n, n, (Edge<Te>*) NULL)); //创建新顶点对应的边向量
		return V.insert(Vertex<Tv>(vertex)); //顶点向量增加一个顶点
	}
	virtual Tv remove(int i) { //删除第i个顶点及其关联边（0 <= i < n）
		for (int j = 0; j < n; j++) //所有出边
			if (exists(i, j)) { delete E[i][j]; V[j].inDegree--; } //逐条删除
		E.remove(i); n--; //删除第i行
		Tv vBak = vertex(i); V.remove(i); //删除顶点i
		for (int j = 0; j < n; j++) //所有入边
			if (Edge<Te>* e = E[j].remove(i)) { delete e; V[j].outDegree--; } //逐条删除
		return vBak; //返回被删除顶点的信息
	}
// 边的确讣操作
	virtual bool exists(int i, int j) //边(i, j)是否存在
	{ return (0 <= i) && (i < n) && (0 <= j) && (j < n) && E[i][j] != NULL; }
// 边的基本操作：查询顶点i不与j之间的联边（0 <= i, j < n且exists(i, j)）
	virtual EType & type(int i, int j) { return E[i][j]->type; } //边(i, j)的类型
	virtual Te & edge(int i, int j) { return E[i][j]->data; } //边(i, j)的数据
	virtual int& weight(int i, int j) { return E[i][j]->weight; } //边(i, j)的权重
// 边的动态操作
	virtual void insert(Te const& edge, int w, int i, int j) { //插入权重为w的边e = (i, j)
		if (exists(i, j)) return; //确保该边尚不存在
		E[i][j] = new Edge<Te>(edge, w); //创建新边
		e++; V[i].outDegree++; V[j].inDegree++; //更新边计数不关联顶点的度数
	}
	virtual Te remove(int i, int j) { //删除顶点i和j之间的联边（exists(i, j)）
		Te eBak = edge(i, j); delete E[i][j]; E[i][j] = NULL; //备分后删除边记录
		e--; V[i].outDegree--; V[j].inDegree--; //更新边计数与关联顶点的度数
		return eBak; //返回被删除边的信息
	}
}

对于任意顶点 i，枚举其所有的邻接顶点 neighbor：

int nextNbr(int i, int j){	//若已枚举至邻居 j，则转向下一邻居
	while((-1 < j)&& !exists(i,--j));	//逆向顺序查找 O（n）
	return j;
}	//改用邻接表可提高至O(1+ outDegree(1))

int firstNbr(int i){
	return nextNbr(i,n);
}	//首个邻居

判断两个顶点之间是否存在一条边：

bool exists(int i, int j){
	return (0 <= i)&&(i < n)&&(0 <= j)&&(j < n) && E[i][j] != NULL;	//短路求值
}	//以下假定exists(i,j)...

Te & edge(int i,int j)	//边(i,j)的数据
	{return E[i][j]->data;}	//O(1)

邻接矩阵的优点包括：
1.可以快速判断任意两个节点之间是否存在边。
2.适用于稠密图（图中边的数量接近节点数量的平方）。

邻接矩阵的缺点：
1.对于稀疏图（图中边的数量远小于节点数量的平方），矩阵中有大量的0，造成空间浪费。
2.插入和删除边的操作比较复杂，需要修改矩阵中的元素。
3.占用的内存空间随着节点数量的增加而快速增加。

广度优先搜索

越早被访问到的顶点， 其邻居优先被选用

从顶点 s 开始的广度优先搜索：
1.访问顶点s；
2.依次访问s所有尚未访问的邻接顶点；
3.依次访问它们尚未访问的邻接顶点；
4…如此反复
5.直至没有尚未访问的邻接顶点

实现

template <typename Tv, typename Te> //广度优先搜索BFS算法（全图）
void Graph<Tv, Te>::bfs ( int s ) { //assert: 0 <= s < n
	reset(); int clock = 0; int v = s; //初始化
	do //逐一检查所有顶点
		if ( UNDISCOVERED == status ( v ) ) //一旦遇到尚未发现的顶点
			BFS ( v, clock ); //即从该顶点出发启动一次BFS
	while ( s != ( v = ( ++v % n ) ) ); //按序号检查，故不漏不重
}

template <typename Tv, typename Te> //广度优先搜索BFS算法（单个连通域）
void Graph<Tv, Te>::BFS ( int v, int& clock ) { //assert: 0 <= v < n
	Queue<int> Q; //引入辅助队列
	status ( v ) = DISCOVERED; Q.enqueue ( v ); //初始化起点
	while ( !Q.empty() ) { //在Q变空之前，不断
		int v = Q.dequeue(); dTime ( v ) = ++clock; //取出队首顶点v
		for ( int u = firstNbr ( v ); -1 < u; u = nextNbr ( v, u ) ) //枚举v的所有邻居u
			if ( UNDISCOVERED == status ( u ) ) { //若u尚未被发现，则
				status ( u ) = DISCOVERED; Q.enqueue ( u ); //发现该顶点
				type ( v, u ) = TREE; parent ( u ) = v; //引入树边拓展支撑树
			} else { //若u已被发现，或者甚至已访问完毕，则
				type ( v, u ) = CROSS; //将(v, u)归类亍跨边
			}
		status ( v ) = VISITED; //至此，当前顶点讵问完毕
	}
}

算法的实质功能，由子算法BFS()完成。对该函数的反复调用，即可遍历所有连通或可达域。仿照树的层次遍历，这里也借助队列Q，来保存已被发现，但尚未访问完毕的顶点。因此，任何顶点在进入该队列的同时，都被随即标记为DISCOVERED（已发现）状态。
BFS()的每一步迭代，都先从Q中取出当前的首顶点v；再逐一核对其各邻居u的状态并做相应处理；最后将顶点v置为VISITED（访问完毕）状态，即可进入下一步迭代。
若顶点u尚处于UNDISCOVERED（未发现）状态，则令其转为DISCOVERED状态，并随即加入队列Q。实际上，每次发现一个这样的顶点u，都意味着遍历树可从v到u拓展一条边。于是，将边(v，u)标记为树边(tree edge），并按照遍历树中的承袭关系，将v记作u的父节点。
若顶点u已处于DISCOVERED状态（无向图)，或者甚至处于VISITED状态（有向图)，则意味着边(v，u)不属于遍历树，于是将该边归类为跨边（cross edge）。
BFS()遍历结束后，所有访问过的顶点通过parent[]指针依次联接，从整体上给出了原图某一连通或可达域的一棵遍历树，称作广度优先搜索树，或简称BFS树（BFS tree)。

复杂度：BFS搜索所使用的空间，主要消耗在用于维护顶点访问次序的辅助队列、用于记录顶点和边状态的标识位向量，累计$\mathcal{O}(n)+\mathcal{O}(n)+\mathcal{O}(e)=\mathcal{O}(n+e)$

时间方面：首先需花费 $\mathcal{O}(n+e)$ 时间复位所有顶点和边的状态。不计对子函数 BFS() 的调用，bfs() 本身对所有顶点的枚举共需O(n)时间。而在对BFS()的所有调用中，每个顶点、每条边均只耗费O(1)时间，累计O(n + e)。

综合起来，BFS搜索总体仅需O(n + e)时间。

深度优先搜索

优先选取最后一个被访问到的顶点的邻居
以顶点s为基点的DFS搜索，将首先访问顶点s；再从s所有尚未访问到的邻居中任取其一，并以之为基点，递归地执行DFS搜索。故各顶点被访问到的次序，类似于树的先序遍历；而各顶点被访问完毕的次序类似于树的后续遍历。

template < typename Tv, typename Te> //深度优先搜索DFS算法（全图）
void Graph<Tv, Te>::dfs(Rank s) { // s < n
    reset(); Rank clock = 0; //全图复位
	for (Rank v = s; v < s + n; v++) //从s起顺次检查所有顶点
	      if (UNDISCOVERED == status(v % n)) //一旦遇到尚未发现者
	          DFS(v % n, clock); //即从它出发启动一次DFS
} //如此可完整覆盖全图，且总体复杂度依然保持为O(n+e)

template < typename Tv, typename Te> //深度优先搜索DFS算法（单个连通域）
void Graph<Tv, Te>::DFS(Rank v, Rank & clock) { // v < n
	dTime(v) = clock++; status(v) = DISCOVERED; //发现当前顶点v
	   for (Rank u = firstNbr(v); -1 != u; u = nextNbr(v, u)) //考查v的每一个邻居u
		      switch (status(u)) { //并视其状态分别处理
		         case UNDISCOVERED: // u尚未发现，意味着支撑树可在此拓展
			            type(v, u) = TREE; parent(u) = v; DFS(u, clock); break;
		         case DISCOVERED: // u已被发现但尚未访问完毕，应属被后代指向的祖先
			            type(v, u) = BACKWARD; break;
		         default: // u已访问完毕（VISITED，有向图），则视承袭关系分为前向边或跨边
			            type(v, u) = (dTime(v) < dTime(u)) ? FORWARD : CROSS; break;
	}
    status(v) = VISITED; fTime(v) = clock++; //至此，当前顶点v方告访问完毕
}

算法的实质功能，由子算法DFS()递归地完成。每一递归实例中，都先将当前节点v标记为DISCOVERED(已发现)状态，再逐一核对其各邻居u的状态并做相应处理。待其所有邻居均已处理完毕之后，将顶点v置为VISITED（访问完毕）状态，便可回溯。
若顶点u尚处于UNDISCOVERED（未发现）状态，则将边(v,u)归类为树边(tree edge)，并将v记作u的父节点。此后，便可将u作为当前顶点，继续递归地遍历。
若顶点u处于DISCOVERED状态，则意味着在此处发现一个有向环路。此时，在DFS遍历树中u必为v的祖先，故应将边(v,u)归类为后向边(back edge)。

这里为每个顶点v都记录了被发现的和访问完成的时刻，对应的时间区间[dTime(v),fTime(v)]均称作v的活跃期（active duration)。实际上，任意顶点v和u之间是否存在祖先/后代的“血缘”关系，完全取决于二者的活跃期是否相互包含。

对于有向图
对于有向图，顶点u还可能处于VISITED状态。此时，只要比对v与u的活跃期，即可判定在DFS树中v是否为u的祖先。若是，则边(v,u)应归类为前向边（forward edge)；否则，二者必然来自相互独立的两个分支，边(v,u)应归类为跨边（cross edge）。

DFS(s)返回后，所有访问过的顶点通过parent[]指针依次联接，从整体上给出了顶点s所属连通或可达分量的一棵遍历树，称作深度优先搜索树或DFS树(DFS tree)。与BFS搜索一样，此时若还有其它的连通或可达分量，则可以其中任何顶点为基点，再次启动DFS搜索。
最终，经各次DFS搜索生成的一系列DFS树，构成了DFS森林（DFS forest) 。

深度优先搜索算法所使用的空间，主要消耗于各顶点的时间标签和状态标记，以及各边的分类标记，二者累计不超过O(n) + O(e) = O(n + e)。
首先需要花费O(n + e)时间对所有顶点和边的状态复位。不计对子函数DFS()的调用，DFS()本身对所有顶点的枚举共需O(n)时间。不计DFS()之间相互的递归调用，每个顶点、每条边只在子函数DFS()的某一递归实例中耗费O(1)时间，故累计亦不过O(n + e)时间。
综合起来，深度优先搜索也可以在O(n + e)时间完成。

DFS 和 BFS 的区别

深度优先搜索（DFS）和广度优先搜索（BFS）是两种常用于图的遍历算法，它们有以下主要区别：

1. 遍历顺序：
   深度优先搜索 (DFS)： 从起始节点开始，沿着一条路径尽可能深入地探索，直到达到叶子节点，然后回溯到上一个节点，再继续探索下一个分支。DFS倾向于先探索深度较深的分支。
   广度优先搜索 (BFS)： 从起始节点开始，首先访问起始节点的所有邻居节点，然后逐层访问与起始节点距离为1、2、3等的节点。BFS倾向于先探索离起始节点近的节点。

2. 数据结构：
   深度优先搜索 (DFS)： 通常使用递归方法或栈数据结构来实现。
   广度优先搜索 (BFS)： 通常使用队列数据结构来实现。

3. 搜索目标：
   深度优先搜索 (DFS)： 主要用于查找路径或判断图中是否存在某个节点，通常不关心最短路径。
   广度优先搜索 (BFS)： 主要用于寻找最短路径或层次遍历，通常用于求解最短路径问题。

4. 内存消耗：
   深度优先搜索 (DFS)： 在最坏情况下，可能需要消耗大量的内存空间，因为它需要递归调用或维护一个深度较深的栈。
   广度优先搜索 (BFS)： 通常需要维护一个队列，因此在内存消耗上可能更高效，但需要考虑队列大小的问题。

5. 时间复杂度：
   深度优先搜索 (DFS)： 在某些情况下，DFS可能会找到解决方案更快，但在最坏情况下，可能需要遍历整个图，时间复杂度为O(V +E)，其中V是节点数量，E是边数量。
   广度优先搜索 (BFS)： 通常用于求解最短路径问题，时间复杂度也为O(V + E)，但在一些情况下，BFS可能会找到解决方案更快。

拓扑排序之零入度算法

拓扑排序是一种用于有向无环图（DAG）的排序算法，其目标是将图中的节点线性排序，使得任何有向边都从左到右指向更大的节点。拓扑排序通常用于表示任务之间的依赖关系，以确保在执行任务时不会出现循环依赖。

基本思想：
1.首先找到图中所有入度为零的节点，将它们添加到拓扑排序的结果中。
2.然后移除这些入度为零的节点及其出边，更新剩余节点的入度。
3.重复步骤1和步骤2，直到所有节点都添加到拓扑排序的结果中，或者发现有向图中存在环路（无法进行拓扑排序）。

#include 
#include 
#include 

using namespace std;

// 图的表示，这里使用邻接表
vector<vector<int>> graph;

// 计算节点的入度
vector<int> calculateIndegree(int numNodes) {
    vector<int> indegree(numNodes, 0);
    for (int i = 0; i < numNodes; i++) {
        for (int neighbor : graph[i]) {
            indegree[neighbor]++;
        }
    }
    return indegree;
}

// 零入度算法的拓扑排序
vector<int> topologicalSort(int numNodes) {
    vector<int> result;
    vector<int> indegree = calculateIndegree(numNodes);
    queue<int> zeroIndegreeNodes;

    // 初始化，将所有入度为零的节点入队
    for (int i = 0; i < numNodes; i++) {
        if (indegree[i] == 0) {
            zeroIndegreeNodes.push(i);
        }
    }

    while (!zeroIndegreeNodes.empty()) {
        int node = zeroIndegreeNodes.front();
        zeroIndegreeNodes.pop();
        result.push_back(node);

        // 移除节点及其出边，更新剩余节点的入度
        for (int neighbor : graph[node]) {
            indegree[neighbor]--;
            if (indegree[neighbor] == 0) {
                zeroIndegreeNodes.push(neighbor);
            }
        }
    }

    // 如果拓扑排序结果包含所有节点，则返回排序结果；否则，表示有环路，返回空向量。
    if (result.size() == numNodes) {
        return result;
    }
    else {
        return vector<int>();
    }
}

int main() {
    int numNodes = 6;
    graph.resize(numNodes);

    // 构建图
    graph[0].push_back(1);
    graph[0].push_back(2);
    graph[1].push_back(3);
    graph[2].push_back(3);
    graph[2].push_back(4);
    graph[3].push_back(5);

    vector<int> sortedNodes = topologicalSort(numNodes);

    if (!sortedNodes.empty()) {
        cout << "拓扑排序结果: ";
        for (int node : sortedNodes) {
            cout << node << " ";
        }
        cout << endl;
    }
    else {
        cout << "图中存在环路，无法进行拓扑排序。" << endl;
    }

    return 0;
}

首先构建了一个有向图的邻接表表示。然后，通过计算每个节点的入度，找到入度为零的节点并将其添加到拓扑排序结果中。接着，移除这些节点及其出边，更新剩余节点的入度。不断重复这个过程，直到完成拓扑排序或发现图中存在环路。

如果图中存在环路，零入度算法将无法完成拓扑排序。

拓扑排序之零出度算法

拓扑排序的零出度算法与零入度算法非常相似，不同之处在于它关注的是节点的出度（即节点指向其他节点的边）。
基本思想：
1.首先找到所有出度为零的节点，将它们添加到拓扑排序的结果中；
2.然后删除这些节点及其出边，继续查找出度为零的节点;
3.以此类推，直到完成整个拓扑排序。

如果图中存在环路，零出度算法也将无法完成拓扑排序。