01背包
01背包的概念
有N件物品和一个容量为V的背包。第i件物品的费用是c[i],价值是w[i]。求解将哪些物品装入背包可使价值总和最大。
从这个题目中可以看出,01背包的特点就是:每种物品仅有一件,可以选择放或不放。
状态转移方程
01背包问题的状态转移方程是:
f[i][v]=max{f[i-1][v],f[i-1][v-c[i]]+w[i]}
其中,即fi表示前i件物品恰放入一个容量为v的背包可以获得的最大价值。
上述方程右边可以理解为两种情况,取最优值.
情况一:第i件不放进去,这时所得价值为:fi-1;
情况二:第i件放进去,这时所得价值为:fi-1]+w[i];
情况二的意思是,如果第i件放进去,那么在容量V-c[i]里就要放进前i-1件物品.(引用自)
案例解析
有编号分别为a,b,c,d,e的五件物品,它们的重量分别是2,2,6,5,4,它们的价值分别是6,3,5,4,6,现在给你个承重为10的背包,如何让背包里装入的物品具有最大的价值总和?
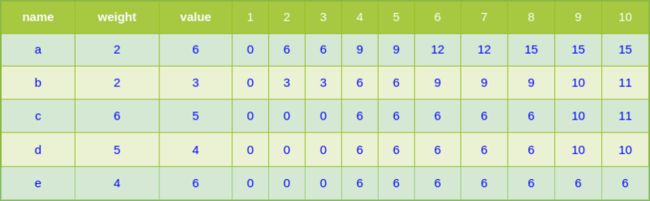
首先要明确这张表是至底向上,从左到右生成的.
只要你能通过找规律手工填写出上面这张表就算理解了01背包的动态规划算法。
为了叙述方便,用e2单元格表示e行2列的单元格,这个单元格的意义是用来表示只有物品e时,有个承重为2的背包,那么这个背包的最大价值是0,因为e物品的重量是4,背包装不了
对于d2单元格,表示只有物品e,d时,承重为2的背包,所能装入的最大价值,仍然是0,因为物品e,d都不是这个背包能装的。(引用自)
编程实现
var n = 5; //物品数量,该参数可以自行设定
var v = 10; //背包体积,该参数可自行设定
var volumArray = [4, 3, 5, 2, 5];//物品体积组成的数组,该参数可自行设定
var valueArray = [9, 6, 1, 4, 1];//物品价值组成的数组,该参数可自行设定
var tempArray = [];
for (let a = 0; a < n; a++) {
tempArray[a] = [];
for (let b = 0; b < v; b++) {
tempArray[a].push(0);
}
}
for (let i = 0; i < n; i++) {
for (let j = 0; j < v; j++) {
tempArray[i][j] = i == 0 ? 0 : tempArray[i - 1][j];
if (i > 0 && j >= volumArray[i - 1]) {
tempArray[i][j] = tempArray[i][j] >= tempArray[i - 1][j - volumArray[i - 1]] + valueArray[i - 1] ? tempArray[i][j] : tempArray[i - 1][j - volumArray[i - 1]] + valueArray[i - 1];
}
}
}
console.log(tempArray[n - 1][v - 1]);
完全背包
完全背包的概念
有N种物品和一个容量为V的背包,每种物品都有无限件可用。
第i种物品的体积是c,价值是w。求解将哪些物品装入背包可使这些物品的体积总和不超过背包容量,且价值总和最大。
状态转移方程
参考上述01背包的转移方程,不难得出:
f[i][v]=max{f[i-1][v-k*c[i]]+k*w[i]|0<=k*c[i]<=v}伪代码实现如下:
for i=1...N
for v=0...V
for k=1...v/w[i]
f[i][v] = max{f[i-1][v],f[i-1][v-k*w[i]]+k*c[i]};案例解析
给你六种面额1,5,10,20,50,100元的纸币,假设每种币值的数量都足够多,编写程序求组成N元的不同组合个数.
function fn (all) {
const arr = [1, 5, 10, 20, 50, 100],
len = arr.length,
res = [];
for (let i = 0; i <= len; i++) {
res[i] = [];
res[i][0] = 1;
}
for (let j = 1; j <= all; j++) {
res[0][j] = 0;
}
for (let i = 1; i <= len; i++) {
for (let j = 1; j <= all; j++) {
res[i][j] = 0;
for (let k = 0; k <= j / arr[i - 1]; k++) {
res[i][j] += res[i - 1][j - k * arr[i - 1]];
}
}
}
return res[len][all];
}