数据结构 | 第十章：散列表 | 字典 | 线性探查 | 链式散列 | LZW编码

10.1 字典

字典是一些形如（k,v）的数对（元素/记录）所组成的集合。其中k是关键字，v是与关键字k对应的值。任意两个数对，其关键字都不等。

若是多重字典，则两个或多个数对可以具有相同的关键字。

10.2 字典的抽象数据类型

ADT

抽象类dictionary

template< class K, class E>
class dictionary
{
    public:
    	virtual ~dictionary(){}
   		
    	//返回true，当且仅当字典为空
    	virtual bool empty() const = 0;
    
    	//返回字典中数对的数目
     	virtual int size() const = 0;
    
    	//返回匹配数对的指针
    	virtual pair<const K,E>* find(const K&) const = 0;
    
    	//删除匹配的数对
    	virtual void erase(const K&) = 0;
    
    	//往字典中插入一个数对
    	virtual void insert(const pair<const K,E>&) = 0;
};

访问字典数对

随机访问（Random Access）

• 按照给定的一个关键字来访问字典中的数对。

顺序访问（Sequential Access）

• 按照关键字的递增顺序逐个访问字典中的数对。
• 顺序访问需要操作：
  • Begin-用来返回关键字最小的数对
  • Next-用来返回下一个数对

字典的线性结构描述

• 线性表描述
• 跳表描述
• 散列表描述

数对类型：pair

• 数对p的关键字：p.first
• 数对p的值：p.second

10.3 线性表描述

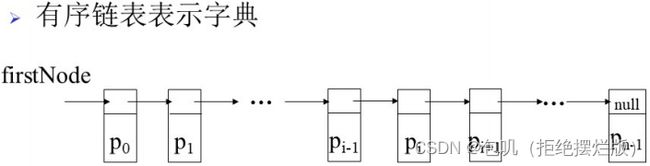
字典用有序线性表：$(p_0,p_1,p_2,...,p_{n-1})$表示，关键字从左到右依次增大。

数组描述

链式描述

template <class K, class E>
struct pairNode
{
    pair<const K, E> element;
    pairNode<K, E>* next;
    pairNode(const pair<const K, E>& thePair):element(thePair){}
    pairNode(const pair<const K, E>& thePair,pairNode<K, E>* theNext):element(thePair) 
    {next = theNext;}
};

类sortedChian

template<class K, class E>
class sortedChain : public dictionary<K, E>
{
    public:
        sortedChain() { firstNode = NULL; dSize = 0; }
        ~sortedChain();
        bool empty() const { return dSize == 0; }
        int size() const { return dSize; }
    	//返回关键字theKey匹配的数对的指针，若不存在匹配的数对，则返回NULL
        pair<const K, E>* find(const K& theKey) const;
    	//删除关键字theKey匹配的数对
        void erase(const K& theKey);
    	//插入一个数对thePair，覆盖已经存在的数对
        void insert(const pair<const K, E>& thePair);
    protected:
        pairNode<K, E>* firstNode;//指向链表第一个节点的指针
        int dSize;//表中的数对个数
};

方法find

返回匹配的数对的指针，如果不存在匹配的数对，则返回NULL

• 从第一个节点开始扫描节点，直到遇到第一个关键字大于等于theKey的节点currentNode或全部判断完为止

• 判断currentNode所指节点中数对的关键字是否等于theKey

currentNode->element.first =theKey

• 若相等，返回数对的指针，否则返回NULL

template<class K, class E>
pair<const K,E>* sortedChain<K,E>::find(const K& theKey) const
{
    pairNode<K,E>* currentNode = firstNode;
    
    //搜索关键字为theKey的数对
    while(currentNode != NULL && currentNode->element.first != theKey)
        currentNode = currentNode->next;
    
    //判断是否匹配
    if(currentNode != NULL && currentNode->element.first == theKey)//找到
        return &currentNode->element;
    
    //无匹配的数对
    return NULL;
}

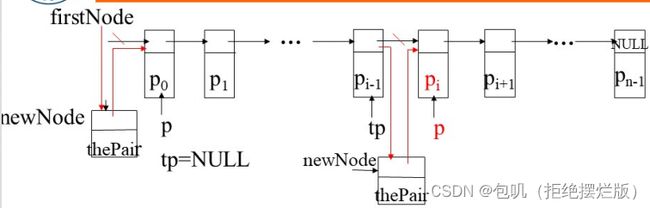
方法insert

在字典中插入一个数对thePair，覆盖已经存在的数对

• 从第一个节点开始，寻找第一个关键字≥theKey的数对

• 若p->element.first == theKey

  • 插入的数对thePair中的值覆盖p->element中的值

    p->element.second= thePair.second;

• 若p->element.first > theKey

  • 新节点newNode <-（插入的数对thePair，p）
  • tp不为空：新节点插入到tp后面tp->next= newNode；
  • tp为空：新节点为首节点firstNode=newNode；

template<class K,class E>
void sortedChain<K,E>::insert(const pair<const K,E>& thePair)
{//往字典中插入thePair,覆盖已经存在的匹配的数对
    pairNode<K,E> *p = firstNode, *tp = NULL;//跟踪p
    //移动指针tp,使thePair可以插在tp的后面
    while(p != NULL && p->element.first < thePair.first)
    {
        tp = p;
        p = p-> next;
    }
    
    //检查是否有匹配的数对
    //情况（1）有匹配的数对
    while(p != NULL && p->element.first == thePair.first)
    {//替换旧值
        p->element.second = thePair.second;
        return;
    }
    //情况（2）无匹配的数对，为thePair建立新节点
    pairNode<K,E> *newNode = new pairNode<K,E>(thePair, p);
    //在tp之后插入新节点
    if(tp == NULL) firstNode = newNode;
    else tp->next = newNode;
    dSize++;//因为插进来一个，所以数对数量++
    return;
}

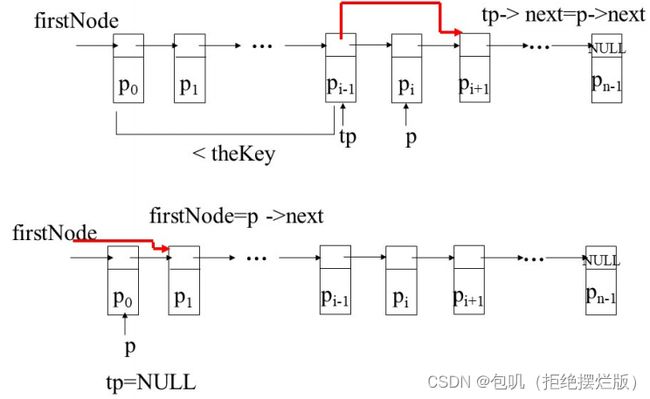
方法erase

template<class K, class E>
void sortedChain<K,E>::erase(const K& theKey)
{//删除关键字为theKey的数对
    pairNode<K,E> *p = firstNode, *tp = NULL;
    //搜索关键字为theKey的数对
    while(p !=NULL && p->element.first < theKey)
    {
        tp = p;
        p = p->next;
    }//tp就是追踪用的，刚好在p的前一个
    
    //确定是否匹配
    if(p != NULL && p->element.first == theKey)
    {//找到一个匹配的数对
        //从链表中删除p
        if(tp == NULL) firstNode = p->next;//p是第一个节点
        else tp->next = p->next;
        delete p;
        dSize--;
    }
}

10.5 散列表描述

10.5.1 理想散列

散列（Hashing）：字典的一种描述方法。

散列方法：它用一个散列函数（也称哈希函数）把字典的数对映射到一个散列表的具体位置。

非理想情况：多个关键字映射到同一个位置

理想情况：

• 数对p的关键字为k，f是散列函数
• 数对p在散列表中的位置为f(k)

理想散列

假定散列表中的每一个位置最多只能存放一个数对

散列表操作：

• 查找（find）：计算出f(k)，然后看表中f(k)处是否有关键字为k的数对。

• 插入（insert）：计算出f(k)，把数对放在f(k)位置

• 删除（erase）：计算出f(k)，把表中f(k)位置置为空

在理想情况下，散列表操作时间复杂度∶ O（1）

10.5.2 散列函数和散列表

• 桶：散列表的每一个位置叫一个桶

• 起始桶：对关键字为k的数对，f(k)是起始桶

• 散列表的长度或大小：桶的数量。

• 散列函数

  • 好的散列函数

    • 均匀散列函数：映射到一个桶里的关键字大致相同
    • 良好的散列函数：性能较好的均匀散列函数

  • 在多种散列函数中，最常用的是除余散列

    • 它的形式如下：f(k) = k % D
    • D：散列表的大小（即位置数）
      • 散列表的位置索引：0 ~ D-1
      • D的选择对于散列的性能有着重大的影响（D等于桶的个数b）。
      • 当D为素数或D是没有小于20的素数因子时，可以使性能达到最佳。
    • k：非整型关键字
      • 计算k之前，把k转换成非负整数

• 冲突和溢出

  • 当两个不同的关键字所对应的起始桶相同时，就是冲突发生了。

  • 如果存储桶没有空间存储一个新数对，就是溢出发生了。

  • 当映射到散列表中的任何一个桶里的关键字数量大致相等时，冲突和溢出的平均数最少。均匀散列函数就是这样的函数。

  • 解除溢出的常用方法

    • 线形探查
    • 链式散列

10.5.3 线性探查

对应实验8.1

hashTable类

template<class K,class E>
class hashTable <K,E>:public dictionary<K,E>
{
    public:
		hashTable(int theDivisor = 11);
		~hashTable() { delete[] table; }
		bool empty() const { return dSize == 0; }
    	int size() const { return dSize; }
    	//返回关键字theKey匹配的数对的指针，若不存在则返回NULL
    	pair<const K,E>* find(const K&)const;
    	//在字典中插入一个数对thePair，若存在关键字相同的数对，则覆盖
 		void insert(const pair<const K,E>&);
	protected:
		int search(const K&)const;
    	pair<const K，E>**table;//散列表
		int divisor;//散列函数的除数
		hash<K>hash;//把类型k映射到一个非负整数
    	int dSize;//字典中数对的个数
}

构造函数

template<class K, class E>
hashTable<K,E>::hashTable(int theDivisor)
{
    divisor = theDivisor;
    dSize = 0;
    
    //分配和初始化散列表数组
    table = new pair<const K,E>* [divisor];
    for(int i = 0; i < divisor; i++)
    	table[i] = NULL;
}

方法search

• 首先搜索关键字为k的起始桶f(k)
• 接着对表中后继桶进行搜索，直到发生以下情况：
  • （1）存有关键字为k的桶已找到，即找到了要搜索的数对
  • （2）到达一个空桶
  • （3）又回到起始桶f(k)。
• 若发生情况（2）和（3），则说明表中没有关键字为k的数对。

template<class K, class E>
int hashTable<K,E>::search(const K& theKey) const
{//搜索一个公开地址散列表，查找关键字为theKey的数对；
 //如果匹配的数对存在，返回它的位置
 //否则，如果散列表不满，则返回关键字为theKey的数对可以插入的位置
	int i = (int)hash(theKey) % divisor;//起始桶
    int j = i;//从起始桶开始
    do
    {
        if(table[j]==NULL || table[j]->first == theKey)
            return j;
        j = (j+1) % divisor;//下一个桶
    }while (j != i);//结束条件判断：是否返回到起始桶
    return j;//表满
}

方法find

template<class K, class E>
pair<const K,E>* hashTable<K,E>::find(const K& theKey) const
{//返回匹配数对的指针，如果匹配数对不存在，则返回NULL
    //搜索散列表
    int b = search(theKey);
    //判断table[b]是否是匹配数对
    if(table[b] == NULL || table[b]->first != theKey)
        return NULL;//没有找到
    return table[b];//找到匹配数对  
}

方法insert

• 调用b=search（theKey）

  • （1）b号桶是空桶，数对thepair插入到b号桶中；

  • （2）b号桶不空：

    • 如果b号桶中的关键字为thepair.first（table[b]->first=thepair.first），用thepair.second覆盖b号桶中数对的值；

    • 否则，表已满，抛出一个异常；

template<class K, class E>
void hashTable<K,E>::insert(const pair<const K,E>& thePair)
{//把数对thePair插入字典，若存在关键字相同的数对，则覆盖；若表满，则抛出异常
    //搜索散列表，查找匹配的数对
    int b = search(thePair.first);
    //检查匹配的数对是否存在
    if(table[b] == NULL)
    {
        //没有匹配的数对，而且表不满
        table[b] = new pair<const K,E>(thePair);
        dSize++;
    }
    else
    {//检查是否有重复的关键字数对或是否表满
        if(table[b]->first == thePair.first)
        {
            table[b]->second = thePair.second;
        }
        else
            throw hashTableFull();//表满
    }
}

方法erase

• 执行搜索操作，找到关键字为k的桶

• 在完成一次删除操作之后，必须保证上述的搜索过程仍然能够正常进行。不能仅仅把表中相应的位置置为空。

  例如
  如果删除了关键字58，那么35这个关键字就永远也找不到了，因为删除58之后，桶4被置位空。当查找35的时候首先查找桶2、再对比桶3、再对比桶4，发现桶4为空，那么就退出查找（此时35显示未查找到，实际上存在于散列表中)

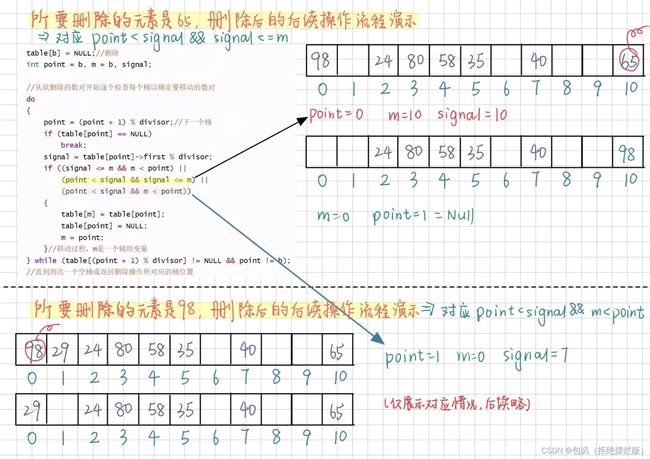
• 删除的方法：

  方法（1）：从欲删除的数对开始逐个检查每个桶以确定要移动的数对，直到到达一个空桶或返回删除操作所对应的桶位置

  方法（2）：为每个桶增加一个NeverUsed域

//以下是方法（1）
template <class K, class E>
void hashTable<K, E>::erase(K& theKey)
{
	//搜索散列表，查找匹配的数对
    int b = search(theKey);
    if (table[b] == NULL || table[b]->first != theKey)
        return NULL;//没有找到
    else
    {
        table[b] = NULL;//删除  
        int point = b, m = b, signal;
        
        //从欲删除的数对开始逐个检查每个桶以确定要移动的数对
        do
        {
            point = (point + 1) % divisor;//下一个桶 
            if (table[point] == NULL)
                break;
            signal = table[point]->first % divisor;
            if ((signal <= m && m < point) || 
                (point < signal && signal <= m) || 
                (point < signal && m < point))
            {
                table[m] = table[point];
                table[point] = NULL;
                m = point;
            }//移动过程，m是一个辅助变量 
        } while (table[(point + 1) % divisor] != NULL && point != b);
        //直到到达一个空桶或返回删除操作所对应的桶位置
    }
}

删除检查时三种情况图

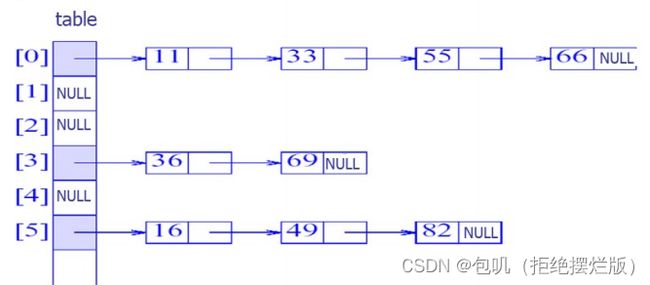
10.5.4 链式散列

对应实验8.2

• 设一个桶可以放无限多个数对，散列表中的桶用一个链表来配置。

• 一个链表上的数对是具有同样起始桶的数对

• 查找（find）：
  • 计算起始桶号为f(k) = k % D；搜索该桶所对应的链表.
• 插入（insert）：
  • 计算f(k)；搜索；插入。 由于每次插入都要首先进行一次搜索，因此把链表按照升序排列比无序排列会更有效。■
• 删除（erase）：
  • 计算f(k)；搜索；删除

小结

链式描述和线性探查比较

1. 线性探查空间少

2. 使用链表时的平均性能要优于使用线性探查

比较

10.6 应用——文本压缩

LZW压缩

• 压缩方法：基于原始数据，创建一个字典，字典中所存放的是文本中的字符串与其编码的映射。然后，用字典中的编码来替代原始数据中相应字符串。

• 压缩规则：

  • 开始，为该文本文件中所有可能出现的字母分配一个代码，构成初始字典
  • LZW压缩器不断地在输入文件的未编码部分中寻找在字典中出现的最长的前缀p，输出前缀p相应的代码，若输入文件中的下一个符号为c，则为pc分配一个代码，并插入字典。

• 压缩实现：

  //设当前前缀p为空，读取下一个字符c；
  循环（当前字符串pc不为空）
  {
      if（当前字符串pc在字典中）
  		当前前缀p = 当前字符串pc;
   	else
      {
          将当前字符串pc插入到字典中;
          输出当前前缀p的编码;
          p=c;
      }
  	读取下一个字符c;
  }
  输出最后一个当前前缀p的编码;
  

• 示例

LZW解压缩

• 压缩方法：

  • 把分配给单一字母的代码插入字典中
  • 输入第一个代码，用相应的文本（第一个代码一定对应于一个单一的字母）代替。
  • 设当前输入代码为p，q为p前面的代码。两种情况：
    • 当p在字典中时
      • 找到与p相关的文本text(p)并输出。
      • text(q)fc(p)插入字典
    • 当p不在字典中，此时只会是一种情况
      • text(p) = text(q)fc(q),(p,text(p))插入字典
      • 代码串：qp 对应文本串：text(q)text(q)fc(q)

• 压缩实现：

  (1)把分配给单一字母的代码插入字典中。
  (2)输入第一个代码q，输出相应的文本（第一个代码一定对应于一个单一的字母）(3)循环:
  	输入下一个代码p;
  	if(p在字典中)
  	{
          输出代码p对应的文本串text(p);
          将text(q)fc(p)及代码插入到字典中
      }
  	else
      {
  		text(p)=text(q)fc(q);
  		输出代码p对应的文本串text(q)fc(q);
          将text(q)fc(q)及代码插入到字典中
      }
  	q=p;
  

  实现：