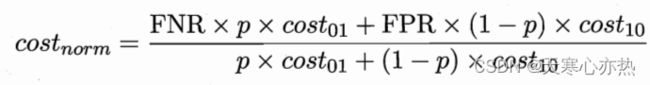机器学习-模型评估与选择（第2章）课后习题
1习题
1.1第1题
数据集包含 1000 个样本, 其中 500 个正例、 500 个反例, 将其划分为包含 70% 样本的训练集和30% 样本的测试集用于留出法评估, 试估算共有多少种划分方式。
答：“留出法”（hold-lout)直接将数据集D划分为两个互斥的集合。训练集和测试集的划分要尽可能保持数据分布的一致性。根据题目要求，需要抽取700个训练样本作为训练集，300个测试样本作为测试集，正例与反例的比例为1：1，即训练集中有350个正例和350个反例，测试集中有150个正例和150个反例。共有
种。
1.2第2题
数据集包含100个样本，其中正、反例各一半，假定学习算法所产生的模型是将新样本预测为训练样本较多的类别（训练样本数相同时进行随机猜测），试给出用10折交叉验证法和留一法分别对错误率进行评估所得的结果。
答：10折交叉检验:由于每次训练样本中正反例数目一样，所以讲结果判断为正反例的概率也是一样的，所以错误率的期望是50%。留一法：如果取一个正例作为测试样本，则训练样本中正例与反例的比例为49：50，此时模型对测试样本的预测结果为反例，错误率为1;如果取一个反例作为测试样本，则训练样本中正例与反例的比例为50：49，此时模型对测试样本的预测结果为正例，错误率为1。综上所述，期望错误率为1。
1.3第3题
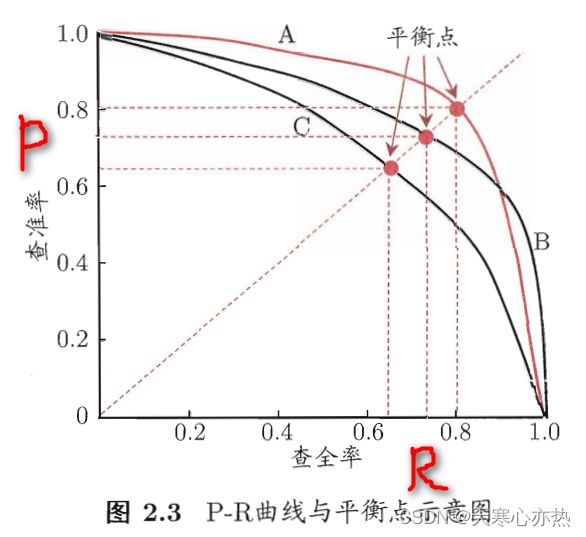
若学习器A的F1值比学习器B高，试析A的BEP值是否也比B高。
答：
F1值在二维坐标内的曲线上任意可取的点都可计算得到。
BEP则是曲线上确定的一点。平衡点（Break-Event Point，简称BEP）就是这样一个度量，它是 查准率=查全率 时的取值。
现在看学习器A和学习器B交叉的右半部分，假设A上有点（0.85，0.5），B上有点（0.9，0.5）。则计算得：
学习器A的F1(A)=(2*0.85*0.5)/(0.85+0.5)=0.630
学习器B的F1(B)=(2*0.9*0.5)/(0.9+0.5)=0.643
有：F1(B)>F1(A)
所以由B的F1(B)大于A的F1(A)，并不能得出B的BEP大于A的BEP。
1.4第4题
试述真正例率（TPR）、假正例率（FPR）与查准率（P）、查全率（R）之间的联系。
答：
查全率（R)：真实正例被预测为正例的比例。R=TP/(TP+FN)
真正例率（TPR）:真实正例被预测为正例的比例。TPR=TP/(TP+FN)
显然查全率（R）=真正例率（TPR）
查准率（P）:预测为正例的实例中真实正例的比例。P=TP/(TP+FP)
假正例率（FPR）:真实反例被预测为正例的比例。FPR=FP/(FP+TN)
查全率越大，查准率往往越低；查准率越高，查全率往往越低。
1.5第5题
试证明式子：
机器学习（西瓜书）第二章 模型评估与选择 课后习题 - 简书 (jianshu.com)
1.6第6题
试述错误率与 ROC 曲线的联系。
答：通常我们把分类错误的样本数占样本总数的比例称为错误率（error rate）。
ROC曲线上的任意一点都是对应着(FPR，TPR)
TPR=TP/(TP+FN)
FPR=FP/(FP+TN)
而错误率对应着
故而错误率对着每一点的不同而不同
1.7第7题
试证明任意一条ROC曲线都有一条代价曲线与之对应，反之亦然。
答：
真正例率：
假正例率：
假反例率：
由定义可以知道TPR与FPR都是由0上升到1，那么FNR则是由1下降到0。
每条ROC曲线都会对应一条代价曲线，由于第一条代价线段是（0，0），（1，1），最后是（0，1）（1，0）。
所有代价线段总会有一块公共区域，这个区域就是期望总体代价，而这块区域的边界就是代价曲线，且肯定从（0，0）到（1，0）。
在有限个样本情况下，ROC是一条折线，此时根据代价曲线无法还原ROC曲线。但若是理论上有无限个样本，ROC是一条连续的折线，代价曲线也是连续的折线，每个点的切线可以求出TPR与FNR，从而得到唯一的ROC曲线。
1.8第8题
答：
规范化：将原来的度量值转换成无量纲的值。通过将属性数据按照比例缩放，通过一个函数将给定属性的整个值域映射到一个新的值域中，即每个旧的值都被一个新的值替代。
Min-max规范化：
等比例缩小：
原数据的偏移量：
整个公式的意思是：将原数据的偏移量等比例缩小，再在新范围的最小值上加上缩小后的偏移量，即可得出新数据的值。
优点：保留了原数据之间偏移量的关系；可以指定数据规范化后的取值范围；是计算复杂度最小的一个方法。
缺点：需要预先知道规范后的最大最小值；若原数据新增数据超越原始范围（最大最小范围），则会发生“越界”，需要重新计算所有之前的结果；若原数据有的值离群度很高(即使得原数据最大或最小值很大)，规范后的大多数数据会特别集中且不易区分。
z-score规范化：
公式表示原数据减去所有原数据的均值
,再除以标准差
,即为规范后的数据。
将公式变形后知，z-score规范化，其实是在计算每个数据相较于均值的偏差距离平方占所有偏差距离平方和的比例。
优点:每次新增或删除原数据，其均值和方差均可能改变，需要重新进行计算；根据其就算原理易知，规范化后的数据取值范围基本在[-1,1],数据之间分布较为密集，对离群点敏感度相对低一些；计算量相对更大。
1.9第9题
略
1.10第10题
略
参考文章：
[1] 周志华. 机器学习.清华大学出版社. 2016 年
https://max.book118.com/html/2020/1229/8006134067003032.shtm
https://blog.csdn.net/cherryc2015/article/details/60132563
https://www.docin.com/p-2296476862.html
https://blog.csdn.net/huzimu_/article/details/123306748
https://www.zhihu.com/question/337049681
https://blog.csdn.net/u014134327/article/details/94603249