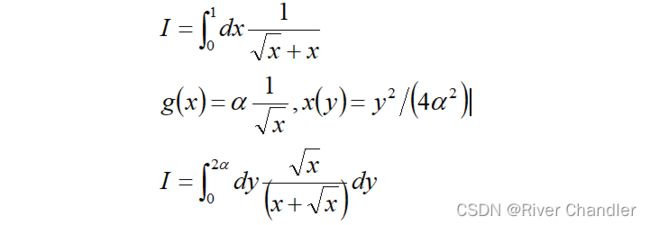计算物理专题----蒙特卡洛积分实战

Part one 蒙特卡洛积分计算案例

import numpy as np
import matplotlib.pyplot as plt
import pandas as pd
from scipy.stats import norm, kstest

np.random.seed(0)
def integrate(a,b,n=100):
    x = np.random.uniform(a,b,n)
    total = sum(np.exp(x))
    return (b - a) * total / n



Num = 10000
F = np.zeros(Num)
for i in range(Num):
    result = integrate(0,1) 
    F[i] = result    
df = pd.DataFrame({'score':F})
bins = np.arange(1.61,1.83,0.001)  # 箱的边界值
df['score_bin'] = pd.cut(df['score'], bins)
count = df['score_bin'].value_counts()
x = [(i.left + i.right) / 2 for i in count.index]
y = count.values/sum(count.values)
# 绘制散点图
plt.scatter(x,y,s=1,c="green",label="10000 I(100) calcs")

F = np.zeros(Num)
for i in range(Num):
    result = integrate(0,1,n=500) 
    F[i] = result    
df = pd.DataFrame({'score':F})
bins = np.arange(1.61,1.83,0.001)  # 箱的边界值
df['score_bin'] = pd.cut(df['score'], bins)
count = df['score_bin'].value_counts()
x = [(i.left + i.right) / 2 for i in count.index]
y = count.values/sum(count.values)
# 绘制散点图
plt.scatter(x,y,s=1,c="red",label="10000 I(500) calcs")

F = np.zeros(Num)
for i in range(Num):
    result = integrate(0,1,n=1000) 
    F[i] = result    
df = pd.DataFrame({'score':F})
bins = np.arange(1.61,1.83,0.001)  # 箱的边界值
df['score_bin'] = pd.cut(df['score'], bins)
count = df['score_bin'].value_counts()
x = [(i.left + i.right) / 2 for i in count.index]
y = count.values/sum(count.values)
# 绘制散点图
plt.scatter(x,y,s=1,c="blue",label="10000 I(1000) calcs")

########

##Num = 100000
##F = np.zeros(Num)
##for i in range(Num):
##    result = integrate(0,1) 
##    F[i] = result    
##df = pd.DataFrame({'score':F})
##bins = np.arange(1.61,1.83,0.001)  # 箱的边界值
##df['score_bin'] = pd.cut(df['score'], bins)
##count = df['score_bin'].value_counts()
##x = [(i.left + i.right) / 2 for i in count.index]
##y = count.values/sum(count.values)
##plt.scatter(x,y,s=1,c="red",label="10000 I calcs")
####


plt.legend()
plt.savefig("hist-plot-4.jpg")
plt.show()
##print(count)
##import csv
##header = ["fit"]
##rows = [[i] for i in F]
##
##with open('1.csv','w',newline="") as file:
##    writer = csv.writer(file)
##    writer.writerow(header)
##    writer.writerows(rows)

Final Result：1.718
Real Result： 1.71828 ERROR EASTIMATE：10^-4

• 蒙特卡洛方法的误差通常可以通过增加模拟次数来减小。具体来说，当我们重复运行模拟并计算出相应的输出后，我们可以计算这些输出的均值和方差，并根据这些数据来估计误差值。如果我们希望减小误差，可以增加模拟次数，这样均值和方差都会更加准确，从而使误差更小。

Part 2 重要抽样 分层抽样

        重要抽样积分和分层抽样积分是数值积分中常用的两种方法，以获得更精确的结果。

        重要性抽样积分涉及从不同于原始分布的概率分布中抽样，但对最终结果贡献较大的区域赋予更大的权重。换句话说，该算法选择更有可能对积分结果做出贡献的样本，并赋予它们比其他样本更高的权重。当原始分布难以采样或对最终结果贡献最大的区域很小时，这尤其有用。

        例如，考虑f(x)从a到b的积分。我们可以从与f(x)|成比例的分布中抽样，而不是从区间[a,b]中均匀抽样。这意味着具有较高的|f(x)|值的区域将被更频繁地采样，并在最终结果中被赋予更高的权重。

        分层采样整合则是将整合区域划分为若干子区域，并从每个子区域分别采集样本。这确保了所有区域的采样都是平等的，而不管该区域的被积数的值是多少。

        例如，考虑f(x,y)在区域[a,b] x [c,d]上的积分。我们可以把这个区域分成4个更小的区域，每个区域分别采样。这确保了我们从所有区域得到相等的样本，当被积量在积分区域上表现出高方差时特别有用。

        重要抽样积分和分层抽样积分都是数值积分的重要技术，它们的适用性取决于需要解决的问题。在被积量高度可变或难以采样的情况下，重要性抽样往往更有效，而分层抽样在被积量在整个积分区域表现出高度可变性的情况下是有用的。

        我们将a,b两问的结果用下表展示处理

Num = 5e4,k=5e3,n=10	Simple MC	Stratified sampling
Round 1	1.3741162994281273	1.3741162994281273
Stats(round for 200)
figure
mean	1.3873987598712592	1.387267505078644
std	0.022234190779851584	0.02282746853161396

find the optimal n

Optimal	RESULT	ERROR
N=18	1.3868879367871603	1e-4

import numpy as np
np.random.seed(0)

#exact value 1.38629
def MC(a=0,b=1,n=50000):
    f = lambda x:1/(x+x**0.5)
    x = np.random.uniform(a,b,n)
    return sum(f(x))*(b-a)/n

#stratified sampling
def SS(a=0,b=1,n=10,k=5000):
    x1 = np.linspace(a,b,k+1)[:k]
    x2 = np.linspace(a,b,k+1)[1:]
    SUM = 0
    for i in range(k):
        SUM += MC(a=x1[i],b=x2[i],n=n)
    return SUM

import matplotlib.pyplot as plt
##S = np.array([SS() for i in range(200)])
##M = np.array([MC() for i in range(200)])
##
##print(np.mean(S))
##print(np.mean(M))
##
##print(np.std(S))
##print(np.std(M))
##
##plt.hist(S,label="S")
##
##plt.legend()
##plt.savefig("P3-1.jpg")
##plt.pause(0.01)
##plt.cla()
##plt.hist(M,label="M")
##plt.legend()
##plt.savefig("P3-2.jpg")
##plt.pause(0.01)
S = []
for n in range(5,20):
    S.append(SS(n=n,k=int(50000/n)))
S = np.array(S)

---

import numpy as np
import matplotlib.pyplot as plt
np.random.seed(0)


def f(x):
    return 1 / (np.sqrt(x) + x)

# 积分区域划分
num_strata = 5000
strata_size = 1 / num_strata

# 每个子区域采样点数
num_samples_per_stratum = 10

# 计算每个子区域的采样点
samples = []
for i in range(num_strata):
    stratum_start = i * strata_size
    stratum_end = (i + 1) * strata_size
    stratum_samples = np.random.uniform(stratum_start, stratum_end, num_samples_per_stratum)
    samples.extend(stratum_samples)

# 计算每个采样点的函数值
values = f(samples)

# 计算积分近似值
integral_approx = np.mean(values)

print("Approximate integral value:", integral_approx)

---

Part 3 积分实战

	CHOOSE	ERROR	N^(-1/2)
	Best when alpha = 0.5	0.00167	0.3536
	Num of Nodes is 8
	Best when alpha = 0.6	0.04752	0.3015
	Num of Nodes is 8
	Best when alpha = 0.7	0.00167	0.3536
	Num of Nodes is 8
	Best when alpha = 0.8	0.00167	0.3536
	Num of Nodes is 8

---

Part 6 高维积分

        Now,we will implement a MC method to find the volume of the N-dimensional sphere for the arbitrary dimension N and the sphere radius R.

        让我们估算一下一个25D的球体需要多少次实验才能得到精确的结果

1/(((1/25)**0.5)**25)=2.980232238769527e+17

        所以我们不可能从0-1开始取值，这样的运算量是我们不能接受的。

        利用C语言，我们创建了多个线程尽可能得将数值计算的极限推进到了13阶左右（计算用时在一分钟左右）

        同时我们希望使用Python语言进行编程，方便我们进行并行运算：并行运算的程序我们已在附件中给出了，遗憾的是，该方法仅能支持13阶左右的运行，远远达不到25阶的需求。（计算用时在一分钟左右）

        我们需要解决维度灾难问题。应该要从数学角度解决他。

                首先我们改用L1距离运算。稍微加快计算的速度

                其次，我们使用一个低差异序列（Sobol）序列生成更加均匀的随机数

运算结果

Dim		17		18		19		20		21	22
Theory		0.1409		0.0821		0.0466		0.0258		0.0139	0.0073
Calculate		0.1409		0.0821		0.0466		0.0258		0.0139	0.0073
23	24		25		26		27
0.0038	0.0019		0.0009		0.000466		0.000223
0.0038	0.0019		0.0009		0.000456		0.000198

import numpy as np
import scipy.special as spi
import matplotlib.pyplot as plt
np.random.seed(0)
import time


def prod(n):
    p = 1
    for i in range(1,n+1):
        p *= i
    return p

def f(n):
    if n%2==0:
        k = int(n/2)
        return np.pi**(k)/prod(k)
    elif n%2==1:
        k = int((n-1)/2)
        return np.pi**k*prod(k)*2**n/prod(n)

def main(Num=1e8,dim=4):
    assert(dim>=2),"dim should greater than 2!!!"
    Sum = 0
    #start = time.time()
    for i in range(int(Num)): 
        x = np.random.random(dim)
        p = sum(x**2)
        if p<=1:
            Sum += 1
    #end = time.time()
    #print("Used:",end-start)
    #print("Volume:",Sum/Num*(2**dim))
    #print("Theory:",f(dim))
    print(Sum)
    return Sum/Num*(2**dim),f(dim)

Dim = [20,21,22,23,24,25,26]
V = [0 for i in range(len(Dim))]
F = [0 for i in range(len(Dim))]


for i in range(len(Dim)):
    s = time.time()
    V[i],F[i] = main(dim=Dim[i])
    e = time.time()
    print(e-s)

    
plt.scatter(range(len(Dim)),V,c="red")
plt.scatter(range(len(Dim)),F,c="blue")
plt.plot(range(len(Dim)),V,c="red",label="volume")
plt.plot(range(len(Dim)),F,c="blue",label="Theory")
plt.legend()
plt.pause(0.01)


def main(Num=1e8,dim=4):
    Sum = 0
    for i in range(int(Num)): 
        x = np.random.random(dim)
        p = sum(x**2)
        if p<=1:
            Sum += 1
    print(Sum)
    return Sum/Num*(2**dim),f(dim)

---

main.py 

import datetime
import numpy as np

import multiprocessing as mp
 
    
def final_fun(name,param):
    dim = param
    Num = int(5*1e4)
    Sum = np.random.random((dim,Num))**2
    Sum = sum(Sum[:,:])
    Sum = len(np.where(Sum<=1)[0])
    
    return {name: Sum}
 
 
if __name__ == '__main__':

    dim = 20
    
    start_time = datetime.datetime.now()
 
    num_cores = int(mp.cpu_count())
    
    pool = mp.Pool(num_cores)
    param_dict = {'task1': dim,
                  'task2': dim,
                  'task3': dim,
                  'task4': dim,
                  'task5': dim,
                  'task6': dim,
                  'task7': dim,
                  'task8': dim,
                  'task9': dim,
                  'task10': dim,
                  'task11': dim,
                  'task12': dim,
                  'task13': dim,
                  'task14': dim,
                  'task15': dim,
                  'task16': dim}
    
    results = [pool.apply_async(final_fun, args=(name, param)) for name, param in param_dict.items()]
    
    results = [p.get() for p in results]
 
    end_time = datetime.datetime.now()
    use_time = (end_time - start_time).total_seconds()
 
    print("多进程计算 共消耗: " + "{:.2f}".format(use_time) + " 秒")
    print(results)

---

利用拉丁超立方体采样生成在高维更加均匀的随机数

拉丁超立方体采样的步骤如下：

        1.对于每个维度，将采样区间均匀地划分为相等的子区间。例如，如果要生成100个样本点，那么将采样区间[0, 1]划分为100个子区间，每个子区间的长度为1/100。

        2.在每个维度的每个子区间内，随机选择一个点作为采样点。可以使用均匀分布的随机数生成器来生成这些随机点。

        3.重复步骤2，直到在每个维度上都选择了一个采样点。

import numpy as np
np.random.seed(0)

def latin_hypercube_sampling(dimensions,num_samples):
    samples = np.zeros((num_samples,dimensions))

    intervals = np.linspace(0,1,num_samples+1)
    
    for i in range(dimensions):
        offsets = np.array([np.random.uniform(intervals[np.random.randint(0,num_samples+1)],intervals[np.random.randint(0,num_samples+1)]) for i in range(num_samples)])
        samples[:,i] = offsets
    
    return samples

if __name__ == '__main__':
    dimensions = 25
    num_samples = 1000
    
    # Perform Latin Hypercube Sampling
    samples = latin_hypercube_sampling(dimensions, num_samples)
    
    # Calculate mean and variance for each dimension
    means = np.mean(samples, axis=0)
    variances = np.var(samples, axis=0)
    
    # Print results
    print("Means:", means)
    print("Variances:", variances)