Day69:283. 移动零、11. 盛最多水的容器、42. 接雨水
283. 移动零
leetcode链接:https://leetcode.cn/problems/move-zeroes/
给定一个数组 nums,编写一个函数将所有 0 移动到数组的末尾,同时保持非零元素的相对顺序。
请注意 ,必须在不复制数组的情况下原地对数组进行操作。
示例 1:
输入: nums = [0,1,0,3,12]
输出: [1,3,12,0,0]
示例 2:
输入: nums = [0]
输出: [0]
提示:
1 <= nums.length <= 104
-231 <= nums[i] <= 231 - 1
进阶:你能尽量减少完成的操作次数吗?
这题就是一个典型的快慢指针问题,类似于从数组中删除指定元素。快指针依次遍历,慢指针用来存放元素。思路就是先把所有的0元素删除,再在数组末位填充0,代码如下:
class Solution {
public:
void moveZeroes(vector<int>& nums) {
int slow = 0;
for(int i = 0 ; i < nums.size(); i++){
if(nums[i] != 0){
nums[slow++] =nums[i];
}
}
//把剩下的位置填充为0
for(int i = slow; i < nums.size(); i++){
nums[i] = 0;
}
}
};
11.盛最多水的容器
给定一个长度为 n 的整数数组 height 。
有 n 条垂线,第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
这题是贪心算法,
-
接雨水
给定 n 个非负整数表示每个宽度为 1 的柱子的高度图,计算按此排列的柱子,下雨之后能接多少雨水。
示例 1:
输入:height = [0,1,0,2,1,0,1,3,2,1,2,1]
输出:6
解释:上面是由数组 [0,1,0,2,1,0,1,3,2,1,2,1] 表示的高度图,在这种情况下,可以接 6 个单位的雨水(蓝色部分表示雨水)。
示例 2:
输入:height = [4,2,0,3,2,5]
输出:9
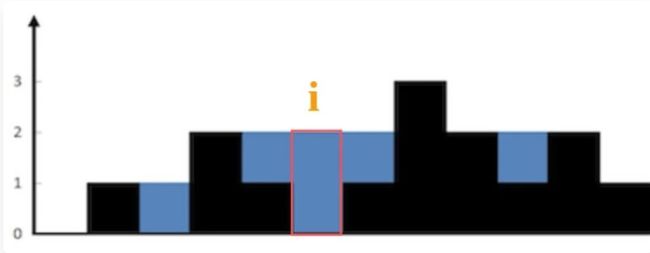
对于这种问题,我们不要想整体,而应该去想局部。仅仅对于位置 i,能装下多少水呢?
能装 2 格水,因为 height[i] 的高度为 0,而这里最多能盛 2 格水,2-0=2。
为什么位置 i 最多能盛 2 格水呢?因为,位置 i 能达到的水柱高度和其左边的最高柱子、右边的最高柱子有关,我们分别称这两个柱子高度为 l_max 和 r_max;位置 i 最大的水柱高度就是 min(l_max, r_max)。
也就是说:
water[i] = min(
# 左边最高的柱子
max(height[0..i]),
# 右边最高的柱子
max(height[i..end])
) - height[i]
根据该思路写一个暴力解法。
暴力解法
class Solution {
public:
int trap(vector<int>& height) {
int res = 0;
for(int i = 1; i < height.size() - 1; i++){//这样才能保证左右都有柱子
int leftMax= 0, rightMax = 0;
for (int j = i; j < height.size(); j++)
rightMax = max(rightMax, height[j]);
// 找左边最高的柱子
for (int j = i; j >= 0; j--)
leftMax = max(leftMax, height[j]);
cout<< leftMax << ',' << rightMax << endl;
res += max(0, min(leftMax,rightMax) - height[i]);
}
return res;
}
};
时间复杂度O(n2),实际上不需要每次都遍历,可以借助备忘录。
这里实际上res加的时候时候不需要和0比较,因为在计算 l_max 数组的时候是取「自己高度」和「目前左边最高」的最大值,因此 l_max[i] >= height[i] 是恒成立的。r_max 同理。
备忘录
不用每次都计算left和right,计算一次就好,存储在两个数组中:
class Solution {
public:
int trap(vector<int>& height) {
if (height.size() == 0) {
return 0;
}
int res = 0;
vector<int> leftMax(height.size(), 0);
vector<int> rightMax(height.size(), 0);
leftMax[0] = height[0];
rightMax[height.size() - 1] = height[height.size() - 1];
for(int i = 1; i < height.size() - 1; i++){//这样才能保证左右都有柱子
leftMax[i] = max(height[i], leftMax[i - 1]);
}
for(int i = height.size() - 2; i >= 0; i--){
rightMax[i] = max(height[i], rightMax[i + 1]);
}
for(int i = 1; i < height.size() - 1; i++){
res += min(leftMax[i],rightMax[i]) - height[i];
}
return res;
}
};
把时间复杂度降低为 O(N),已经是最优了,但是空间复杂度是 O(N)。双指针法可以把空间复杂度降到O(1)。
双指针法
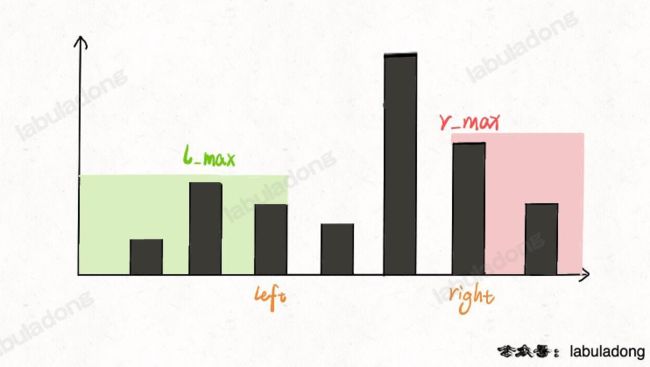
之前不管是暴力解法还是备忘录,leftMax和rightMax分别代表 height[0..i] 和 height[i..end] 的最高柱子高度:
而在双指针法中,代表的是 height[0..left] 和 height[right..end] 的最高柱子高度:
我们只在乎 min(l_max, r_max)。对于上图的情况,我们已经知道 l_max < r_max 了,至于这个 r_max 是不是右边最大的,不重要。重要的是 height[i] 能够装的水只和较低的 l_max 之差有关。
最终代码:
class Solution {
public:
int trap(vector<int>& height) {
int left = 0, right = height.size() - 1;
int leftMax = 0, rightMax = 0;
int res = 0;
while (left < right) {
leftMax = max(leftMax, height[left]);
rightMax = max(rightMax, height[right]);
// res += min(leftMax, rightMax) - height[i]
if (leftMax < rightMax) {
res += leftMax - height[left];
left++;
} else {
res += rightMax - height[right];
right--;
}
}
return res;
}
};
11. 盛最多水的容器
给定一个长度为 n 的整数数组 height 。有 n 条垂线,
第 i 条线的两个端点是 (i, 0) 和 (i, height[i]) 。
找出其中的两条线,使得它们与 x 轴共同构成的容器可以容纳最多的水。
返回容器可以储存的最大水量。
说明:你不能倾斜容器。
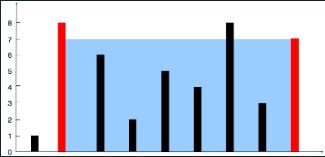
输入:[1,8,6,2,5,4,8,3,7] 输出:49
解释:图中垂直线代表输入数组 [1,8,6,2,5,4,8,3,7]。
在此情况下,容器能够容纳水(表示为蓝色部分)的最大值为 49。
跟上面的题类似,直接贴代码:
class Solution {
public:
int maxArea(vector<int>& height) {
int res = 0;
int left = 0, right = height.size() - 1;
while(left < right){
res = max(res, min(height[left], height[right]) * (right - left));
if(height[left] < height[right]){
left++;
}else{
right--;
}
}
return res;
}
};
这里要注意双指针的移动顺序,为什么是往height[i]小的那边移动?因为矩形的最大面积是由最短的那条边决定的:如果移动较低的那一边,那条边可能会变高,使得矩形的高度变大,进而就「有可能」使得矩形的面积变大;相反,如果你去移动较高的那一边,矩形的高度是无论如何都不会变大的,所以不可能使矩形的面积变得更大。
总结
感觉这样复习还是太零散没有体系了,从明天开始,还是按照模块来,先把原来的题二刷掉,然后再找拓展题。