数据结构与算法:排序算法(1)
目录
冒泡排序
思想
代码实现
优化
鸡尾酒排序
优缺点
适用场景
快速排序
介绍
流程
基准元素选择
元素交换
1.双边循环法
使用流程
代码实现
2.单边循环法
使用流程
代码实现
3.非递归实现
排序在生活中无处不在,看似简单,背后却隐藏着多种多样的算法和思想;
根据时间复杂度的不同,主流的排序算法可以分为三大类:
1.时间复杂度为O(n^2)的排序算法
冒泡排序
选择排序
插入排序
希尔排序
2.时间复杂度为O(nlogn)的排序算法
快速排序
归并排序
堆排序
3.时间复杂度为线性的排序算法
计数排序
桶排序
基数排序
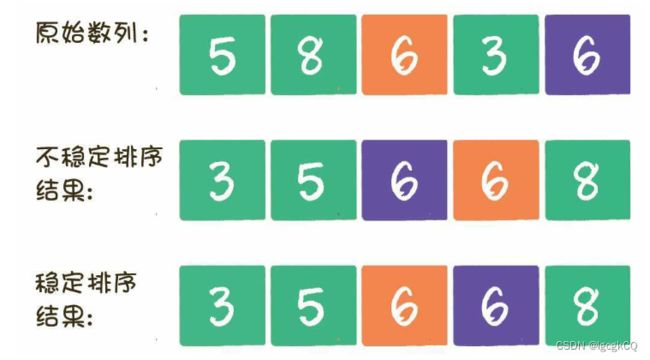
根据稳定性:稳定排序、不稳定排序(如果值相同的元素在排序后仍然保持着排序前的顺序,则这样的排序算法是稳定排序;如果值相同的元素在排序后打乱了排序前的顺序,则这样的排序算法是
不稳定排序)
冒泡排序
冒泡排序,是一种基础的交换排序;这种排序算法的每一个元素都可以像小气泡一样,根据自身大小,一点一点地向着数组的一侧移动
思想
把相邻的元素两两比较,当一个元素大于右侧相邻元素时,交换它们的位置;当一个元素小于或等于右侧相邻元素时,位置不变
元素9作为数列中最大的元素,就像是汽水里的小气泡一样,“漂”到了最右侧;再经过多轮排序,所有元素都是有序的。
冒泡排序是一种稳定排序,值相等的元素并不会打乱原本的顺序。由于该排序算法的每一轮都要遍历所有元素,总共遍历(元素数量-1)轮,所以平均时间复杂度是O(n^2);
代码实现
public static void main(String[] args){
int[] array = new int[]{5,8,6,3,9,2,1,7};
bubbleSort(array);
System.out.println(Arrays.toString(array));
}
public static void bubbleSort(int array[]){
for(int i = 0; i < array.length - 1; i++){
for(int j = 0; j < array.length - i - 1; j++){
int tmp = 0;
if(array[j] > array[j+1]){
tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
}
}
}
}使用双循环进行排序。外部循环控制所有的回合,内部循环实现每一轮的冒泡处理,先进行元素比较,再进行元素交换
优化
利用布尔变量作为标记。如果在本轮排序中,元素有交换,则说明数列无序;如果没有元素交换,则说明数列已然有序,然后直接跳出大循环
public static void bubbleSort(int array[]){
for(int i = 0; i < array.length - 1; i++){
boolean isSorted = true;
for(int j = 0; j < array.length - i - 1; j++){
int tmp = 0;
if(array[j] > array[j+1]){
tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
isSorted = false;
}
}
if(isSorted){
break;
}
}
}鸡尾酒排序
鸡尾酒排序的元素比较和交换过程是双向的;排序过程就像钟摆一样,第1轮从左到右,第2轮从右到左,第3轮再从左到右……
public static void main(String[] args){
int[] array = new int[]{5,8,6,3,9,2,1,7};
bubbleSort(array);
System.out.println(Arrays.toString(array));
}
public static void bubbleSort(int array[]){
int tmp = 0;
for(int i = 0; i < array.length/2; i++){
//有序标记,每一轮的初始值都是true
boolean isSort = true;
//奇数轮,从左向右比较和交换
for(int j = i; j < array.length - i - 1; j++){
if(array[j] > array[j+1]){
tmp = array[j];
array[j] = array[j+1];
array[j+1] = tmp;
//有元素交换,所以不是有序的,标记变为false
isSort = false;
}
}
if(isSort){
break;
}
//在偶数轮之前,将isSorted重新标记为true
isSort=true;
//偶数轮,从右向左比较和交换
for(int j=array.length-i-1; j>i; j--){
if(array[j] < array[j-1]){
tmp = array[j];
array[j] = array[j-1];
array[j-1] = tmp;
//因为有元素进行交换,所以不是有序的,标记变为false
isSort = false;
}
}
if(isSort){
break;
}
}
}代码外层的大循环控制着所有排序回合,大循环内包含2个小循环,第1个小循环从左向右比较并交换元素,第2个小循环从右向左比较并交换元素
优缺点
优点:能够在特定条件下,减少排序的回合数
缺点:代码量几乎增加了1倍
适用场景
大部分元素已经有序的情况
快速排序
介绍
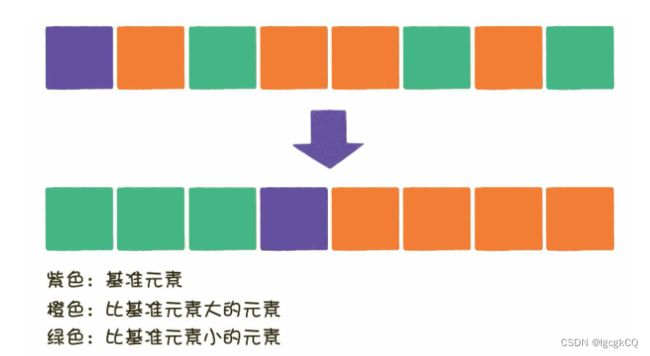
快速排序也属于交换排序,通过元素之间的比较和交换位置来达到排序的目的。快速排序则在每一轮挑选一个基准元素,并让其他比它大的元素移动到数列一边,比它小的元素移动到数列的另一边,从而把数列拆解成两个部分;
这种思路叫做分治法;
流程
在分治法的思想下,原数列在每一轮都被拆分成两部分,每一部分在下一轮又分别被拆分成两部分,直到不可再分为止
每一轮的比较和交换,需要把数组全部元素都遍历一遍,时间复杂度是O(n)。
基准元素选择
基准元素:在分治过程中,以基准元素为中心把其他元素移到它的左右两边。
1.直接选择数列的第1个元素
2.随机选择一个元素
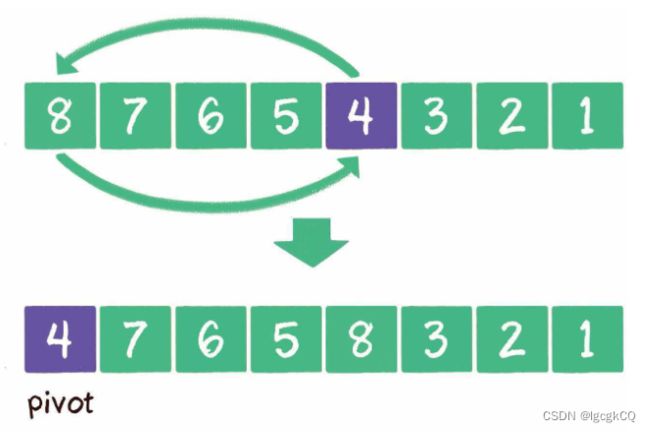
可以随机选择一个元素作为基准元素,并且让基准元素和数列首元素交换位置
元素交换
选定了基准元素以后,我们要做的就是把其他元素中小于基准元素的都交换到基准元素一边,大于基准元素的都交换到基准元素另一边。
有两种实现元素交换的方法:双边循环法、单边循环法
1.双边循环法
实现了元素的交换,让数列中的元素依据自身大小,分别交换到基准元素的左右两边。
使用流程
1.选定基准元素pivot,并且设置两个指针left和right,指向数列的最左和最右两个元素
2.从right指针开始,让指针所指向的元素和基准元素做比较。如果大于或等于pivot,则指针向左移动;如果小于pivot,则right指针停止移动,切换到left指针
3.轮到left指针行动,让指针所指向的元素和基准元素做比较。如果小于或等于pivot,则指针向右移动;如果大于pivot,则left指针停止移动
4.指针大于基准元素时,所指定的元素进行交换,并切换指针
5.当左、右指针重合时,把重合点的元素和基准元素进行交换
代码实现
public static void main(String[] args){
int[] array = new int[]{5,8,6,3,9,2,1,7};
bubbleSort(array, 0, array.length-1);
System.out.println(Arrays.toString(array));
}
public static void bubbleSort(int[] arr, int startIndex,int endInde){
//递归结束:startIndex >= endInde时
if(startIndex >= endInde){
return;
}
//得到基准元素
int pivotIndex = partition(arr, startIndex, endInde);
//根据基准元素,分成两部分进行递归排序
bubbleSort(arr,startIndex,pivotIndex-1);
bubbleSort(arr,pivotIndex+1,endInde);
}
/**
* 双边循环法,返回基准元素位置
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
* @return
*/
private static int partition(int[] arr, int startIndex,int endIndex){
//取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = arr[startIndex];
int left = startIndex;
int right = endIndex;
while (left != right){
//控制right 指针比较并左移
while(left pivot){
right--;
}
//控制left 指针比较并右移
while(left pivot){
left++;
}
if(left < right){
int p = arr[left];
arr[left] = arr[right];
arr[right] = p;
}
}
//pivot 和指针重合点交换
arr[startIndex] = arr[left];
arr[left] = pivot;
return left;
} 2.单边循环法
双边循环法从数组的两边交替遍历元素,虽然更加直观,但是代码实现相对烦琐。而单边循环法则简单得多,只从数组的一边对元素进行遍历和交换。
使用流程
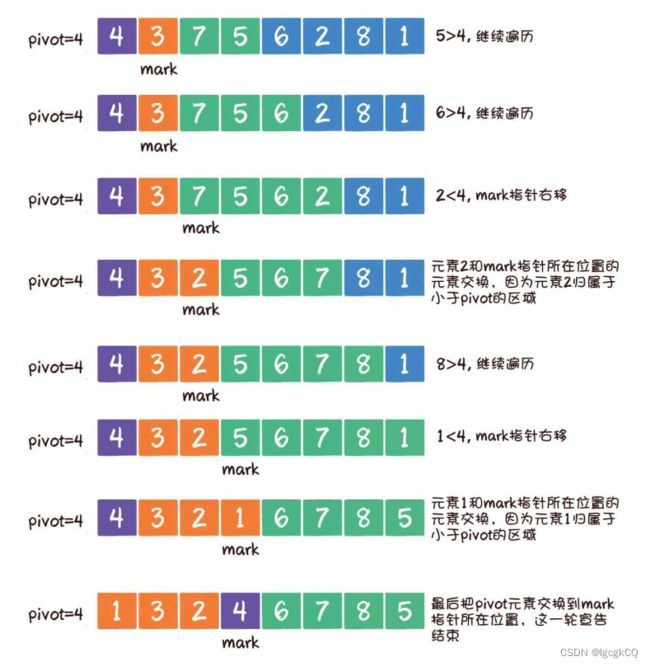
1.首先选定基准元素pivot。同时,设置一个mark指针指向数列起始位置,这个mark指针代表小于基准元素的区域边界
2.从基准元素的下一个位置开始遍历数组;如果遍历到的元素大于基准元素,就继续往后遍历;如果遍历到的元素小于基准元素,则需要做两件事:第一,把mark指针右移1位,因为小于pivot的区域边界增大了1;第二,让最新遍历到的元素和mark指针所在位置的元素交换位置,因为最新遍历的元素归属于小于pivot的区域
代码实现
public static void main(String[] args){
int[] array = new int[]{5,8,6,3,9,2,1,7};
bubbleSort(array, 0, array.length-1);
System.out.println(Arrays.toString(array));
}
public static void bubbleSort(int[] arr, int startIndex,int endInde){
//递归结束:startIndex >= endInde时
if(startIndex >= endInde){
return;
}
//得到基准元素
int pivotIndex = partition(arr, startIndex, endInde);
//根据基准元素,分成两部分进行递归排序
bubbleSort(arr,startIndex,pivotIndex-1);
bubbleSort(arr,pivotIndex+1,endInde);
}
/**
* 双边循环法,返回基准元素位置
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
* @return
*/
private static int partition(int[] arr, int startIndex,int endIndex){
//取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = startIndex;
int mark = endIndex;
for(int i=startIndex+1; i<=endIndex; i++){
if(arr[i]3.非递归实现
把原本的递归实现转化成一个栈的实现,在栈中存储每一次方法调用的参数
public static void main(String[] args){
int[] array = new int[]{5,8,6,3,9,2,1,7};
bubbleSort(array, 0, array.length-1);
System.out.println(Arrays.toString(array));
}
public static void bubbleSort(int[] arr, int startIndex,int endInde){
Stack> quickSortStack = new Stack>();
Map rootParam = new HashMap();
rootParam.put("startIndex", startIndex);
rootParam.put("endIndex", endInde);
quickSortStack.push(rootParam);
while (!quickSortStack.isEmpty()) {
Map param = quickSortStack.pop();
int pivotIndex = partition(arr, param.get("startIndex"),param.get("endIndex"));
if(param.get("startIndex") < pivotIndex -1){
Map leftParam = new HashMap();
leftParam.put("startIndex", param.get("startIndex"));
leftParam.put("endIndex", pivotIndex-1);
quickSortStack.push(leftParam);
}
if(pivotIndex + 1 < param.get("endIndex")){
Map rightParam = new HashMap();
rightParam.put("startIndex", pivotIndex + 1);
rightParam.put("endIndex", param.get("endIndex"));
quickSortStack.push(rightParam);
}
}
}
/**
* 双边循环法,返回基准元素位置
* @param arr 待交换的数组
* @param startIndex 起始下标
* @param endIndex 结束下标
* @return
*/
private static int partition(int[] arr, int startIndex,int endIndex){
//取第1个位置(也可以选择随机位置)的元素作为基准元素
int pivot = startIndex;
int mark = endIndex;
for(int i=startIndex+1; i<=endIndex; i++){
if(arr[i] 非递归方式代码的变动只发生在quickSort方法中。该方法引入了一个存储Map类型元素的栈,用于存储每一次交换时的起始下标和结束下标。
每一次循环,都会让栈顶元素出栈,通过partition方法进行分治,并且按照基准元素的位置分成左右两部分,左右两部分再分别入栈。当栈为空时,说明排序已经完毕,退出循环