潮位分析中高低潮位数据的处理
潮位分析中高低潮位数据的处理
- 基于高低潮数据的潮位插值方法
-
- 三角波(分段线性)插值
-
- 原理
- Matlab实现
- 正弦波插值
-
- 原理
- Matlab实现
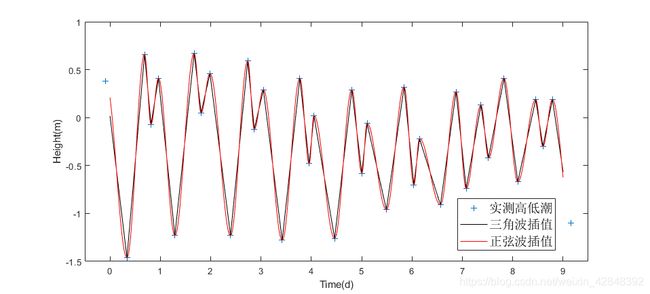
- 结果对比
基于高低潮数据的潮位插值方法
由于在传统的调和分析中,需要输入等间距的潮位数据集,但许多地区的长系列潮位资料仍是以高低潮的形式记录的,即所有数据点为实测高/低潮位,以及对应的出现时间。
故我需要把这样的高低潮数据经过处理(插值法),生成等间距的潮位时间序列。
以下三角波插值和正弦波插值方法参考杨锋的硕士论文《基于高低潮数据的潮汐调和分析方法研究及应用》1。
所用数据集来自中国南部某潮位测站的实测潮位记录。
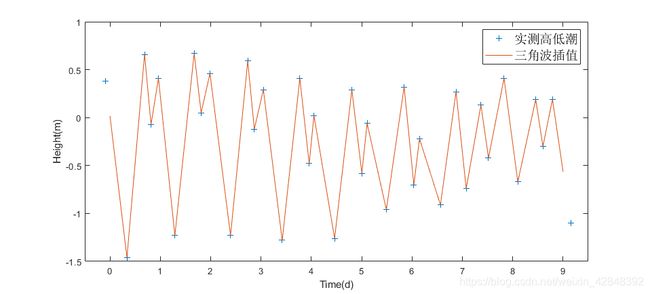
三角波(分段线性)插值
原理
对于已知节点 (x0,y0)和 (x1,y1),在区间[x0,x1]内构造线性函数L(x)以逼近区间内的函数值。
L ( x ) = y 0 + y 1 − y 0 x 1 − x 0 ( x − x 0 ) L(x) = y_{0} + \frac{y_{1}-y_{0}}{x_{1}-x_{0}} (x-x_{0}) L(x)=y0+x1−x0y1−y0(x−x0)
在每一个区间内构建诸如上式的方程,即分段构造线性插值函数。
Matlab实现
选择某测站1月份某9天的实测数据进行插值。
% data_time & data_z : 已知高低潮位数据(时间和潮位)
x1 = linspace(0,9,9*24*60+1);
y1 = interp1(data_time,data_z,x1); %分段线性插值
plot(data_time,data_z,'+',x1,y1), xlabel Time(d), ylabel Height(m);
axis([-0.5 9.5,-1.5,1]);
legend('实测高低潮','三角波插值','fontsize',14);
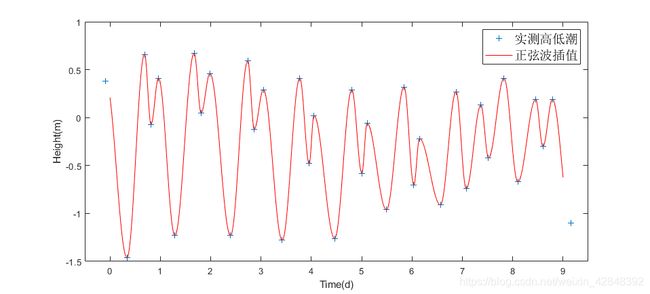
正弦波插值
原理
正弦波插值是以三角函数为插值函数的一种适用于周期函数的插值方法。潮位方程是一个以2k为周期的函数,令潮位方程为y = f(x),则x1,x2,…,xn对应函数值为f(x1),f(x2),…,f(xn)。根据Lagrange插值原理,存在一个多项式pn(x),满足
p ( x k ) = f ( x k ) p(x_{k}) = f(x_{k}) p(xk)=f(xk)
pn(x)为三角函数插值多项式,其次数小于等于n。
取一个n阶三角多项式
t k ( x ) = s i n x − x 0 2 ⋯ s i n x − x k − 1 2 s i n x − x k + 1 2 ⋯ s i n x − x n 2 s i n x k − x 0 2 ⋯ s i n x k − x k − 1 2 s i n x k − x k + 1 2 ⋯ s i n x k − x n 2 , 0 ≤ k ≤ 2 n t_{k}(x) = \frac{sin\frac{x-x_{0}}{2} \cdots sin\frac{x-x_{k-1}}{2}sin\frac{x-x_{k+1}}{2} \cdots sin\frac{x-x_{n}}{2}}{sin\frac{x_{k}-x_{0}}{2} \cdots sin\frac{x_{k}-x_{k-1}}{2}sin\frac{x_{k}-x_{k+1}}{2} \cdots sin\frac{x_{k}-x_{n}}{2}} , 0 \le k \le 2n tk(x)=sin2xk−x0⋯sin2xk−xk−1sin2xk−xk+1⋯sin2xk−xnsin2x−x0⋯sin2x−xk−1sin2x−xk+1⋯sin2x−xn,0≤k≤2n
可简写成
t k ( x ) = ∑ l = 0 , l ≠ k 2 n s i n x − x l 2 s i n x k − x l 2 , 0 ≤ k ≤ 2 n t_{k}(x)=\sum_{l=0,l \ne k} ^{2n} \frac{sin\frac{x-x_{l}}{2}}{sin\frac{x_{k}-x_{l}}{2}}, 0 \le k \le 2n tk(x)=l=0,l=k∑2nsin2xk−xlsin2x−xl,0≤k≤2n
可知,tk(x)满足
t k ( x ) = δ k l l , k = 0 , 1 , 2 … 2 n t_{k}(x) = \delta _{kl} \space \space l,k=0,1,2 \dots 2n tk(x)=δkl l,k=0,1,2…2n
p n ( x ) = ∑ k = 0 2 n f ( x k ) t k ( x ) p_{n}(x) = \sum_{k=0}^{2n} f(x_{k})t_{k}(x) pn(x)=k=0∑2nf(xk)tk(x)
令x = xk ,则有p(xk)=f(xk)。
由潮汐现象的特征可知,一年高低潮数据大概有1400多个,鉴于潮位所受影响因素太多,如果将所有节点都纳入计算的话,函数复杂程度和计算量太大,拟合精度得不到保障,并且毫无必要。当只选取相邻两个节点进行正弦波插值时,插值效果和精度都较为适宜,故最终n取2。即只选择相邻点为端点,采用一阶三角波插值函数p1(x)作整个区间的插值函数。
也有,在区间[xi,xi+1]上
p 1 ( x ) = { y i + 1 − y i 2 s i n [ π x i + 1 − x i ( x − x i + 1 + x i 2 ) ] + y i + 1 + y i 2 if y i ≤ y i + 1 y i − y i + 1 2 s i n [ π x i + 1 − x i ( x − ( x i − x i + 1 − x i 2 ) ) ] + y i + 1 + y i 2 if y i > y i + 1 p_{1} (x)= \begin{cases} {\frac{y_{i+1}-y_{i}}{2} sin[\frac{\pi}{x_{i+1}-x_{i}}(x-\frac{x_{i+1}+x_{i}}{2})]+ \frac{y_{i+1}+y_{i}}{2}} &\text{if } y_i \le y_{i+1} \\ {\frac{y_{i}-y_{i+1}}{2} sin[\frac{\pi}{x_{i+1}-x_{i}}(x-(x_i- \frac{x_{i+1}-x_{i}}{2}))]+ \frac{y_{i+1}+y_{i}}{2}} &\text{if } y_i > y_{i+1} \end{cases} p1(x)={2yi+1−yisin[xi+1−xiπ(x−2xi+1+xi)]+2yi+1+yi2yi−yi+1sin[xi+1−xiπ(x−(xi−2xi+1−xi))]+2yi+1+yiif yi≤yi+1if yi>yi+1
推导过程如下所示。

或将上述两个分段函数表达式整合成如下形式:
p 1 ( x ) = a b s ( y i − y i + 1 ) 2 s i n [ π x − x i x i + 1 − x i + ( 0.5 + q ) π ] + y i + 1 + y i 2 p_{1}(x) = \frac{ abs(y_{i} - y_{i+1}) } {2} sin [\pi \frac{x - x_{i}}{x_{i+1} - x_{i}} + (0.5+q) \pi ] +\frac{y_{i+1}+y_{i}}{2} p1(x)=2abs(yi−yi+1)sin[πxi+1−xix−xi+(0.5+q)π]+2yi+1+yi
式中
q = { 1 if y i ≤ y i + 1 0 if y i > y i + 1 q = \begin{cases} {1} &\text{if } y_i \le y_{i+1} \\ {0} &\text{if } y_i > y_{i+1} \end{cases} q={10if yi≤yi+1if yi>yi+1
Matlab实现
%正弦波(一阶)插值
% data_time & data_z : 已知高低潮位数据(时间和潮位)
%三角函数插值
d1 = size(data_time,1);
x1 = linspace(0,9,9*24*60+1);
% x1为待插值点的x坐标(时间点),数据集包含9天的数据,故从0~9day,每隔1min生成一个点
d2 = size(x1,2);
y1 = zeros(1,d2);
for i = 1:d2
flag = 1;
for j = 1:d1 %判断时间点 x1(i) 属于数据集的哪个区间
if(x1(i)结果对比
http://cdmd.cnki.com.cn/Article/CDMD-10319-1017280624.html ↩︎