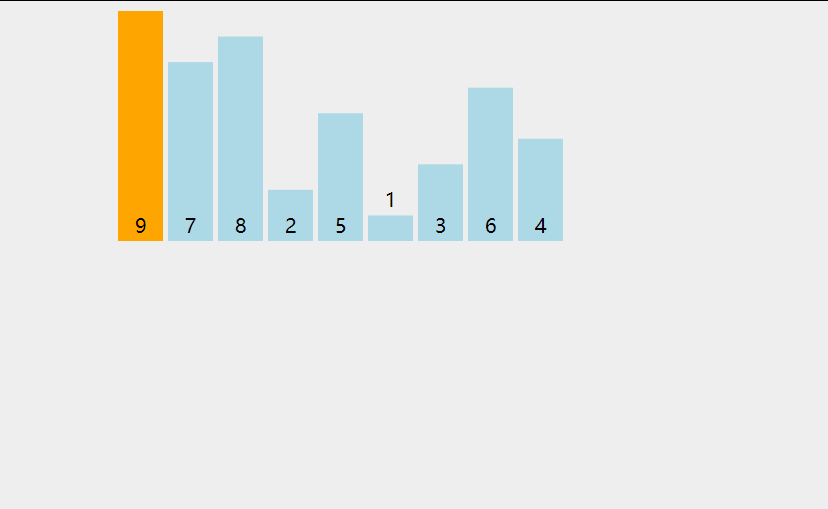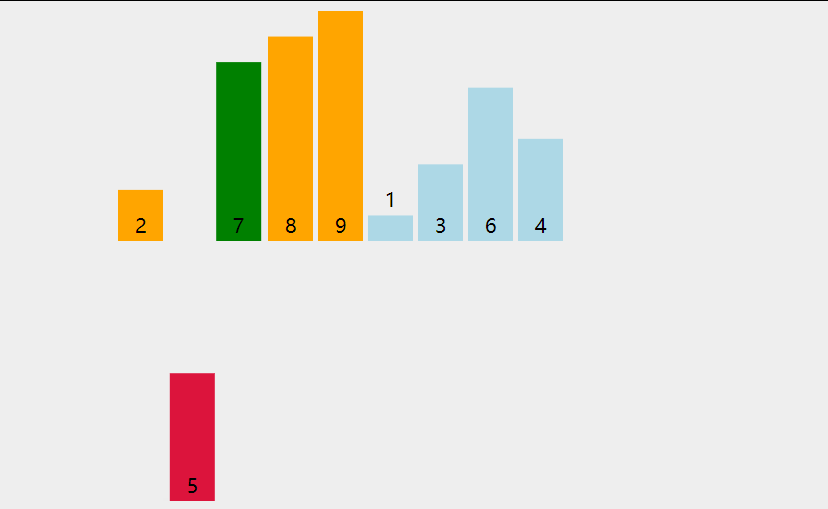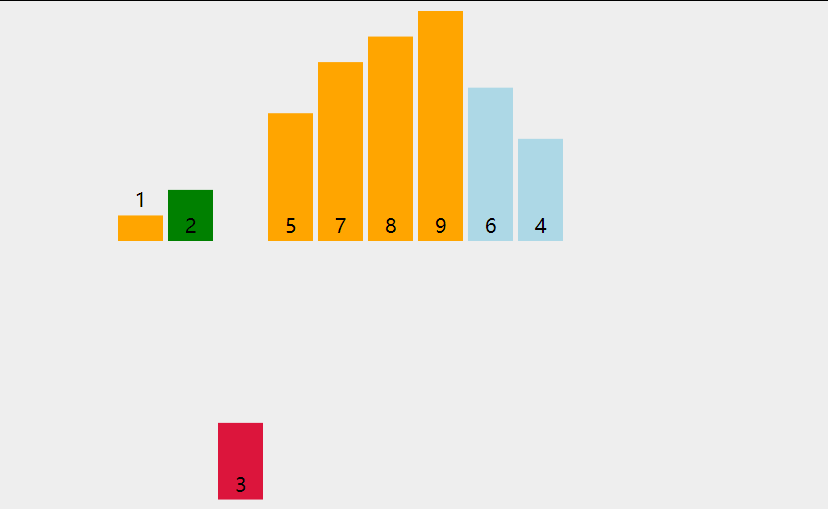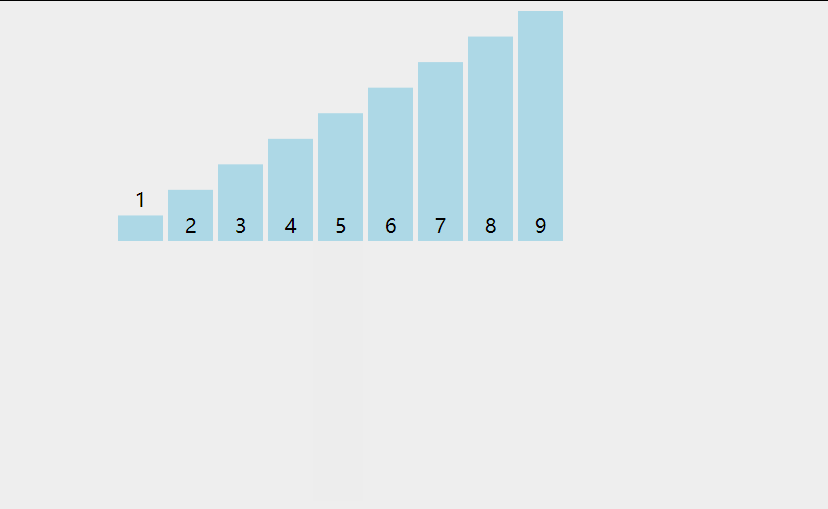一、八大排序（sort）

一、时间复杂度

（一）定义：常数操作

与数据量无关，是一个固定的东西。
一个操作如果和样本数量没有关系，每次都是固定时间内完成的操作，就叫做常数操作。

时间复杂度为一个算法流程中，常数操作数量的一个指标。常用o(读作big o)来表示。具体来说，先要对一个算法流程非常熟悉，然后去写出这个算法流程中，发生了多少常数操作，进而总结出常数操作数量的表达式。

评价一个算法流程的好坏，先看时间复杂度的指标，然后再分析不同数据样本下的实际运行时间，也就是“常数项时间”。

二、空间复杂度

（一）定义：

空间复杂度是对一个算法在运行过程中临时占用存储空间大小的一个量度，同样反映的是一个趋势。

三、排序

（一）选择排序

1.定义

每一次从待排序的数据元素中选出最小（或最大）的一个元素，存放在序列的起始位置，直到全部待排序的数据元素排完。

2.代码

void process(vector<int> &arr) {
    if (arr == nullptr || arr.size() < 2) {
        return ;
    }
    for (int i = 0 ; i < arr.size() - 1; i++) { // 当前位置
        int minIndex = i;
        for (int j = i + 1; j < arr.size(); j++) {
            minIndex = arr[j] < arr[minIndex] ? j : minIndex;
        }
        swap(arr,i,minIndex);
    }
}
void swap(vector<int> &arr,int j,int j) {
    arr[i] = arr[i] ^ arr[j];
    arr[j] = arr[i] ^ arr[j];
    arr[i] = arr[i] ^ arr[j];
}

3.特性

• 容易理解,但是效率太低,实际当中不太使用

• 时间复杂度O(n^2),空间复杂度O(1);

• 不稳定

（二）冒泡排序

1.定义

在要排序的一组数中，对当前还未排好序的范围内的全部数，自上而下对相邻的两个数依次进行比较和调整，让较大的数往下沉，较小的往上冒。即：每当两相邻的数比较后发现它们的排序与排序要求相反时，就将它们互换。

2.代码

void bubbleSort(vector<int> &arr) {
    if (arr == nullptr || arr.size() < 2) {
        return ;
    }
    int n = arr.size();
    for (int i = 0; i < n; i++) { // //控制交换次数
        for (int j = 0; j < n - i - 1; j ++) { // //向后冒泡 ,控制边界
            if(arr[j] > arr[j+1])//如果前一个值大于后一个值,交换
			{
				swap(arr[j],arr[j+1]);
			}		
        }
    }
}

3.特性

• 容易理解
• 时间复杂度O(n^2),空间复杂度O(1)
• 稳定

（三）插入排序

1.定义

插入排序的步骤如下：每次从无序部分中取出一个元素，与有序部分中的元素从后向前依次进行比较，并找到合适的位置，将该元素插到有序组当中。

例：对于数组 [3,2,5,4,2,3,3] 进行插入排序的详细过程：
1、0~0位置上做到有序 ——>就一个数 做到了
2、0~1位置上做到有序 ——>2比3小 2 3互换位置——> [2,3,5,4,2,3,3]
3、0~2位置上做到有序 ——>5比3大 位置不动——> [2,3,5,4,2,3,3]
4、0~3位置上做到有序 ——>4比5小 4 5互换位置——> [2,3,4,5,2,3,3]——>4比3大 位置不动
5、0~4位置上做到有序 ——>2比5小 2 5互换位置——> [2,3,4,2,5,3,3]
  ——>2比4小 2 4互换位置——> [2,3,2,4,5,3,3]——>2比3小 2 3互换位置——> [2,2,3,4,5,3,3]
  2比2相等 位置不动
6、0~5位置上做到有序 ——>3比5小 3 5互换位置——> [2,2,3,4,3,5,3]
  ——>3比4小 3 4互换位置——> [2,2,3,3,4,5,3]——>3比3相等 位置不动
7、0~6位置上做到有序 ——>3比5小 3 5互换位置——> [2,2,3,3,4,3,5]
  ——>3比4小 3 4互换位置——> [2,2,3,3,3,4,5]——>3比3相等 位置不动

2.代码

void insertSort(vector<int> &arr) {
    if (arr == nullptr || arr.size() < 2) {
        return ;
    }
    
    for (int i = 1; i < arr.size(); i++) { // 0 - 0 有序的
    
        for (int j = i - 1; j >= 0 && arr[j] > arr[j + 1] ; j--) { // 想有序
            swap(arr,j, j + 1);
        }
        
    }
}

3.特性

• 元素集合越接近有序，直接插入排序算法的时间效率越高
• 时间复杂度:O(n^2)(情况最差时,即逆序转有序,最好为O(n));
• 空间复杂度:O(1);
• 稳定

（四）归并排序

1.定义

对于一个数组从中点的位置分开，先让左侧部分排好序，再让右边部分排好序，然后整体整合。

将图中左侧部分和右侧部分分别排好序，然后使用两个指针分别从两部分的最左侧开始，在内存中单独开辟一个空间 ，这时我们比较两个指针指向的数的大小，左侧小于等于右侧的时候，将左侧部分指针指向的值拷贝到辅助空间中，然后左侧指针右移一位。如果右侧部分指针指向的值小于左侧的，则将右侧部分指针指向的值拷贝到辅助空间中，然后右侧指针右移一位。依次循环，如果哪侧越界了，将剩下的部分直接拷贝到辅助空间中。将辅助空间拷贝到原数组。

2.代码

3.特性

• 整体就是简单的递归，左边排好序、右边排好序、让整体有序
• 让其整体有序的过程里用了排外序的方法
• 利用master公式来求解时间复杂度
• 归并排序的实质

（五）快速排序

（六）堆排序

（七）基数排序

（八）计数排序