B树(插入、删除)
像之前的二叉搜索树、平衡二叉树、红黑树等都是二叉树,二叉树只能有两个孩子结点。而B-树是一种多路平衡树,不同于二叉树,多路平衡二叉树可以有多个孩子节点。B-树是中序遍历有序的多路平衡树。
阶数:树根节点外的节点所能含有最大子节点数。一颗4阶的节点最多含有四个子节点 。
度数:每个节点含有的子节点数,称为节点的度。
B树:
最小度数:用来衡量B树节点存放键值数的范围。
节点键值数范围:最小度数-1 至 阶-1;
节点子节点数范围:最小度数 至 阶;
节点子节点数 = 节点键值数+1;
根节点的键值数目可为 1;
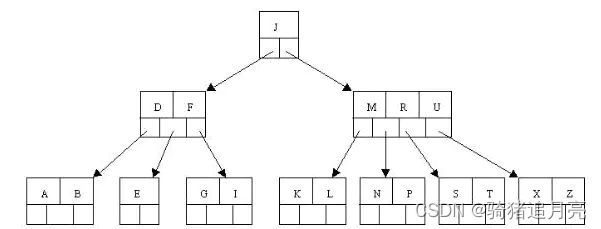
一个四阶B树结构图:
B树的节点结构:
const int T = 2; // 最小度
const int MIN_KEY = T-1;
const int MAX_KEY = 2 * T - 1;
const int MIN_CHILD = MIN_KEY + 1;
const int MAX_CHILD = MAX_KEY + 1; // 阶
typedef int keyType; // 键值类型
// 节点类型
struct BNode {
BNode(bool state = true, int num = 0) :keyNum(num), is_Leaf(state) {
for (int i = 0; i < MAX_CHILD + 1; ++i)
Child[i] = NULL;
}
keyType Key[MAX_KEY + 1]; // 键值域
BNode* Child[MAX_CHILD + 1]; // 孩子
int keyNum; // 节点已存入键值数
bool is_Leaf; // 是否为叶子节点
};
// B-树
class BTree {
friend bool insertFix(BTree& Tree, BNode* node, keyType key);
public:
bool Insert(keyType key); // 插入
bool Delete(keyType key); // 删除
bool Search(keyType key); // 查找
void Traverse(BNode* node); // 遍历
BTree() :Root(NULL) {}
BNode* Root;
};查找:
方法同二叉树一样,需要注意的仅有B树的每一个节点不单单只有一个键值和俩个子树。
// 查找
bool BTree::Search(keyType key) {
if (NULL == Root) return false;
BNode* T = Root;
while (1) {
int i = T->keyNum;
if (T->is_Leaf) {
while (i > 0 && T->Key[i - 1] > key) --i;
if (T->Key[i - 1] == key) return true;
return false;
}
else {
while (i > 0 && T->Key[i - 1] > key) --i;
if (T->Key[i - 1] == key) return true;
T = T->Child[i];
}
}
}插入:
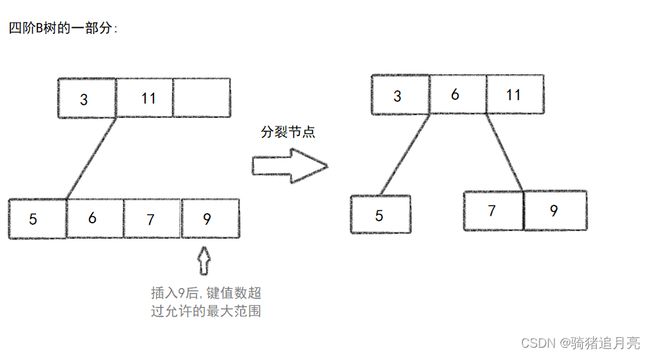
B树的插入思想跟别的树类似,只不过需要在插入键值后判断该节点当前键值数是否已经超过了键值数的最大值,若超过,则需要将该节点分裂。
分裂:
将节点的中间键值上移到父节点处,并让中间键值的左右两部分的键值分别成为中间键值的左右孩子。由于上移一个键值到父节点,需要向上判断是否现需要继续分裂节点。
// 分裂节点( 分裂节点P的pos位置的子节点 )
void splitNode(BNode* P, int pos, BNode* C) {
BNode* LC = new BNode(C->is_Leaf, MIN_KEY); // 新的左孩子
BNode* RC = new BNode(C->is_Leaf, MIN_KEY + 1); // 新的右孩子
// 转移键值
for (int i = 0; i < MIN_KEY; ++i) {
LC->Key[i] = C->Key[i];
RC->Key[i] = C->Key[MIN_KEY + 1 + i];
}
RC->Key[MIN_KEY] = C->Key[MAX_KEY];
// 非叶子节点需要转移子树
if (!C->is_Leaf) {
for (int i = 0; i < MIN_CHILD; ++i) {
LC->Child[i] = C->Child[i];
RC->Child[i] = C->Child[MIN_CHILD + i];
}
}
RC->Child[MIN_CHILD] = C->Child[MAX_CHILD];
// 中间键值上移到父节点
// 父节点pos位置后的键值和子树后移,腾个空位
int i = P->keyNum;
for (; i > pos; --i) {
P->Key[i] = P->Key[i - 1];
P->Child[i + 1] = P->Child[i];
}
P->Key[pos] = C->Key[MIN_KEY]; // 键值上移
P->Child[i] = LC;
P->Child[i + 1] = RC;
++P->keyNum;
}// 插入调整操作
bool insertFix(BTree& Tree, BNode* node, keyType key) {
int i = node->keyNum;
if (node->is_Leaf) { //叶子节点
while (i > 0 && node->Key[i - 1] > key) {
node->Key[i] = node->Key[i - 1]; // 后移腾位
--i;
}
node->Key[i] = key;
++node->keyNum;
if (node->keyNum == MAX_KEY + 1 && node == Tree.Root) { // 插入树根位置 且树根已满
BNode* newRoot = new BNode(); // 新的树根
newRoot->is_Leaf = false;
splitNode(newRoot, 0, node);
Tree.Root = newRoot;
return true;
}
else if (node->keyNum == MAX_KEY + 1) return true; // 已满
return false;
}
else { // 内节点
while (i > 0 && node->Key[i - 1] > key) --i;
int flat = insertFix(Tree, node->Child[i], key);
if (flat) { // 插入的子树已满
splitNode(node, i, node->Child[i]);
}
if (node->keyNum == MAX_KEY + 1 && node == Tree.Root) { // 内节点的树根已满
BNode* newRoot = new BNode(); // 新的树根
newRoot->is_Leaf = false;
splitNode(newRoot, 0, node);
Tree.Root = newRoot;
return true;
}
else if (node->keyNum == MAX_KEY + 1) return true;
return false;
}
}
// 插入
bool BTree::Insert(keyType key){
if (Search(key)) return false; // 已存在
if (NULL == Root) { // 空树
Root = new BNode();
Root->Key[Root->keyNum] = key;
++Root->keyNum;
return true;
}
insertFix(*this, Root, key);
return true;
}删除:
删除操作相比于插入来说,复杂许多,按不同情况来分析;
1.删除的键值所在的节点是内节点。
跟二叉树同情况下思想一样,找到该节点的后继键值,将后继键值赋予给待删键值,转化为删除后继键值(为叶子节点)。由于是内节点,所以必能找到后继键值,且不需要考虑后继键值所在的节点键值数是否大于键值数的最小值(最小度数-1)。
2.删除的键值所在的节点是叶子节点
2.1 删掉键值后,节点的键值数还不小于键值数最小值(最小度数-1),则不需要调整。
2.2 删掉键值后,节点的键值数小于键值数最小值(最小度数-1)
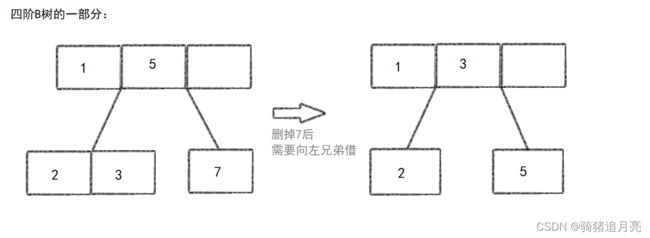
2.2.1 兄弟节点富余,找兄弟节点借一个键值。(不能直接借,需通过父节点中转)
2.2.1.1 找左兄弟借
2.2.1.2 找右兄弟借
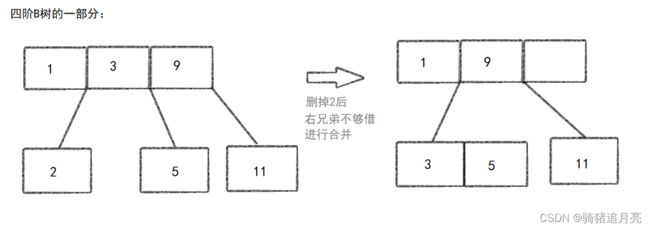
2.2.2 兄弟节点不富余,合并节点。
合并:
将父节点的一个键值下移和子节点合并后,可能会导致父节点的键值小于键值数最小值,使得父节点仍需要继续调整。
// 合并操作
void merge(BNode* P, int pos) {
BNode* LC = P->Child[pos];
BNode* RC = P->Child[pos + 1];
LC->Key[LC->keyNum] = P->Key[pos];
++LC->keyNum;
for (int i = 0; i < RC->keyNum; ++i) {
LC->Key[LC->keyNum + i] = RC->Key[i];
++LC->keyNum;
}
for (int i = pos + 1; i < P->keyNum; ++i) {
P->Key[i-1] = P->Key[i];
P->Child[i] = P->Child[i + 1];
}
--P->keyNum;
}// 删除
bool BTree::Delete(keyType key) {
if (NULL == Root || 0 == Root->keyNum) return false;
BNode* T = Root;
stack NODE;
while (1) {
NODE.push(T);
int i = 0;
while (i < T->keyNum&&T->Key[i] < key) ++i;
if (i < T->keyNum&&T->Key[i] == key) { // 删除键值在该节点中
if (T->is_Leaf) { // 叶子节点,删除
for (; i < T->keyNum - 1; ++i) {
T->Key[i] = T->Key[i + 1];
}
--T->keyNum;
break;
}
else { // 非叶子节点,找后继/也可以找前驱(必存在)
BNode* RC = T->Child[i + 1]; // 右孩子
while (!RC->is_Leaf) RC = RC->Child[0];
T->Key[i] = RC->Key[0];
key = RC->Key[0];
T = T->Child[i + 1];
}
}
else { // 删除节点不在该节点中
T = T->Child[i];
}
}
// 删除后调整
BNode* P = NODE.top();
NODE.pop();
while (!NODE.empty()) {
T = P;
P = NODE.top();
NODE.pop();
if (T->keyNum < MIN_KEY) {
int i = 0;
for (; i <= T->keyNum; ++i) {
if (T == P->Child[i]) break;
}
BNode* LB = i > 0 ? P->Child[i - 1] : NULL;
BNode* RB = i < P->keyNum ? P->Child[i + 1] : NULL;
if (LB&&LB->keyNum > MIN_KEY) { // 左兄弟存在且键值富余
for (int k = T->keyNum; k > 0; --k) {
T->Key[k] = T->Key[k - 1];
}
T->Key[0] = P->Key[i - 1];
++T->keyNum;
P->Key[i - 1] = LB->Key[LB->keyNum - 1];
--LB->keyNum;
}
else if (RB&&RB->keyNum > MIN_KEY) { // 右兄弟存在且键值富余
T->Key[T->keyNum] = P->Key[i];
++T->keyNum;
P->Key[i] = RB->Key[0];
for (int k = 0; k < RB->keyNum - 1; ++k) {
RB->Key[k] = RB->Key[k + 1];
}
--RB->keyNum;
}
else if (LB) { // 左兄弟存在但不富余
merge(P, i - 1);
T = P->Child[i - 1];
}
else if (RB) { // 右兄弟存在但不富余
merge(P, i);
T = P->Child[i];
}
}
}
// 树根被借走,树高 -1
if (Root == P && P->keyNum == 0) {
Root = P->Child[0];
}
return true;
}