数据结构--排序(1)
文章目录
- 排序概念
- 直接插入排序
- 希尔排序
- 冒泡排序
- 堆排序
- 选择排序
- 验证不同排序的运行时间
排序概念
排序指的是通过某一特征关键字(如信息量大小,首字母等)来对一连串的数据进行重新排列的操作,实现递增或者递减的数据排序。
稳定性:假定在待排序的记录序列中,存在多个具有相同的关键字的记录,若经过排序,这些记录的相对次序保持不变,即在原序列中,r[i]=r[j],且r[i]在r[j]之前,而在排序后的序列中,r[i]仍在r[j]之前,则称这种排序算法是稳定的;否则称为不稳定的。
在实际的应用中是非常常见的。
在我们常见的排序算法中,有这几种:
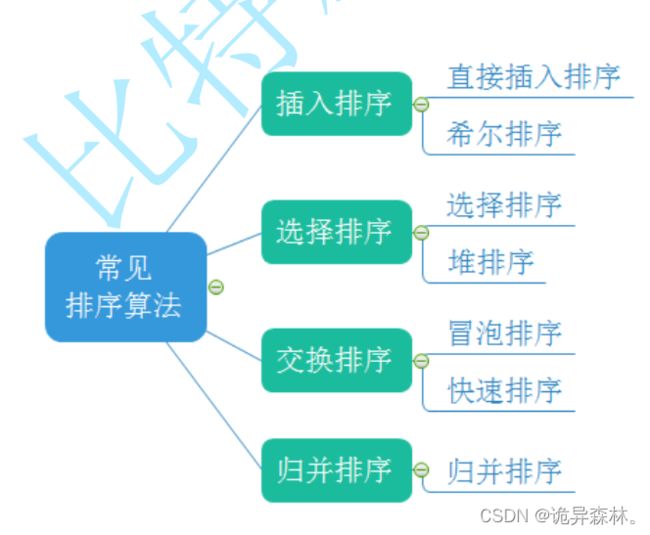
这些排序算法都是通过自身空间,通过不断交换来实现排序的。
直接插入排序
思想:当我们拿到了一组数组时,先将第一个元素定为前序序列,让第二个元素与它对比,以升序为例,大的就放在第一个元素之后,小的就放在第一个元素之前,放完之后,两个元素将成为新的前序序列;接着就是将第三个元素与前序序列的元素比较,比较最大的元素,也就是前序序列的最后一个元素,比它大就将元素向后挪移,为插入数腾出一个元素空间;依此类推。
玩斗地主时从小排到大的就是这种思想:
#include"Sort.h"
void PrintfArray(int* a, int n)
{
for (int i = 0; i < n; i++)
{
printf("%d ", a[i]);
}
printf("\n");
}
//直接插入排序
void InsertSort(int* a, int n)
{
for (int i = 0; i < n - 1; i++)
{
int end = i;
int tmp = a[end + 1];
while (end >= 0)
{
//将数组看作是一个个数插入进去的,从第二个数开始插入
//比较插入数和前序序列最后一个数的大小
//不符合条件就前序序列缩短,一直比较到大于end值停下来
if (a[end] >tmp )
{
a[end + 1] = a[end];
}
else
{
break;
}
end--;
}
a[end + 1] = tmp;
}
}
内循环就是将新插入的数找到合适位置,让出空间,让新的数插入;
时间复杂度:O(N^2)
验证:
void TestInsertSort()
{
int a[] = { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };
InsertSort(a, sizeof(a) / sizeof(a[0]));
PrintfArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
TestInsertSort();
return 0;
}
希尔排序
在上面的直接插入排序中,如果插入数一直大于前序序列,会发现内循环会走的比较快;因为都排序好了,只需要比较前序序列的最后一个元素即可;
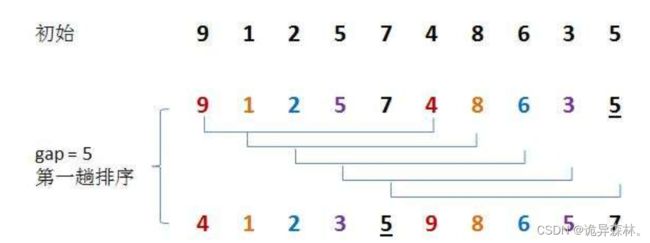
思想:希尔排序中,就是先将一组数组分成几等份,将每一份都进行排序,这样对于下次进行直接插入排序就预先做好了排序,简称预排序;接着不断缩短每一份的长度,一直做着预排序,直到每一份的长度为1时,就相当于上面的直接插入排序。
希尔排序就是对直接插入排序进行优化,通过预排序,让数组的排序比较有序,这样在再次排序时,就会省出会很多时间。
对于gap的取值,一般习惯直接对半取,但现在也有将gap取成三等份的;但实际效果都差不多;
void Swap(int* a, int* b)
{
int tmp = *a;
*a = *b;
*b = tmp;
}
//希尔排序
void ShellSort(int* a, int n)
{
int gap = n;
while (gap > 1)
{
//gap=gap/2;
gap = gap/3 + 1;
for (int i=0; i< n - gap; i ++)
{
int end = i;
int tmp = a[end + gap];
while (end >= 0)
{
if (a[end] > tmp)
{
a[end + gap] = a[end];
end -= gap;
}
else
{
break;
}
}
a[end + gap] = tmp;
}
}
}
1.将tmp与前序序列相比大小,交换,最后将空出的位插入tmp;
2.前序序列扩大了,新增一个数;
3.在不同组中进行直插;
4.进行不断的预排序;
在这里,不是将每一组排完再进行下一组的排序,而是排一组的前序序列之后,跳掉下一组去进行排序到前序序列;gap若取3等份,要加上1,不然可能会出现达不到gap==1的情况,如为8时,gap取到2就停止了;
这里不要看着有很多层循环进行嵌套,实际上它的算法效率是远远高于直接插入排序的,以gap一直取二等份为例,1000个数据也就取10次gap,100万数据也就取20次gap,10亿才取24次gap,所以外层的循环实际次数是不大的,相对如此大的数据几乎可以忽略不计;
验证:
void TestShellSort()
{
int a[]= { 9,1,2,5,7,4,8,6,3,5,1,2,3,5,1,8,3 };
ShellSort(a, sizeof(a)/sizeof(a[0]));
PrintfArray(a, sizeof(a) / sizeof(a[0]));
}
int main()
{
TestShellSort();
return 0;
}
时间复杂度:O(N^1.25) ~ O(1.6*N^1.25)
冒泡排序
思想:通过循环,不断的比较相邻的两个值,将最大的值往后放到最后一个位置,再通过一层循环,进行多躺的比较,总是将最大数往后放即可;
这样最大的数就排好了,以此类推排其他的数字;
//冒泡排序
void BubbleSort(int* a, int n)
{
int mark = 0;
for (int i = 0; i < n - 1; i++)
{
for (int j = 0; j < n -1- i; j++)
{
if (a[j] > a[j + 1])
{
Swap(&a[j], &a[j + 1]);
mark = 0;
}
else
{
mark = 1;
}
}
//表示没有进行交换,已排序好了
if (mark == 1)
{
break;
}
}
}
时间复杂度:O(N^2)
堆排序
堆排序链接处
堆排序之前写过了,这里就不多解释;
void AdjustDown(int* a, int n, int parent)
{
//左孩子
int child = parent * 2 + 1;
while (child<n)
{
//右孩子比左孩子大
if (child + 1 < n && a[child + 1] > a[child])
{
child++;
}
if (a[child] > a[parent])
{
Swap(&a[child], &a[parent]);
parent = child;
child = parent * 2 + 1;
}
else
{
break;
}
}
}
//堆排序
void HeapSort(int* a, int n)
{
//建堆
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
AdjustDown(a, n, i);
}
//交换
int end = n - 1;
while (end>0)
{
Swap(&a[0], &a[end]);
AdjustDown(a, end, 0);
end--;
}
}
时间复杂度:O(N*logN)
选择排序
思想:在数组中找出最大值和最小值的下标,记录它,然后分别与起始与结尾位置进行交换,这样一次就能找出最大值和最小值了,接着缩短数组起始和结尾位置,然后再通过循环依次进行此步骤;
void SelectSort(int* a,int n)
{
int begin = 0;
int end = n - 1;
while (begin < end)
{
int min = begin;
int max = begin;
//找出区间里的max和min
for (int i = begin + 1; i <= end; i++)
{
if (a[i] < a[min])
{
min = i;
}
if (a[i] > a[max])
{
max = i;
}
}
//将最小数放在起始位置
Swap(&a[begin], &a[min]);
//max位置的数一旦被改变,max也需跟随改变
if (max == begin)
{
max = min;
}
Swap(&a[end], &a[max]);
begin++;
end--;
}
}
这里需要注意的是,如果起始点就是最大数时,当最小数与起始位置交换后,那么max表示下标,max不变,仍然指着起始位置的下标,所以需要跟随max的值改变而改变;
O(N^2)
验证不同排序的运行时间
通过10000个数据来验证它们的排序运行时间;
void TestOP()
{
srand(time(NULL));
const int N = 100000;
int* a1 = (int*)malloc(sizeof(int) * N);
int* a2 = (int*)malloc(sizeof(int) * N);
int* a3 = (int*)malloc(sizeof(int) * N);
int* a4 = (int*)malloc(sizeof(int) * N);
int* a5 = (int*)malloc(sizeof(int) * N);
//赋值
for (int i = 0; i < N; i++)
{
a1[i] = rand();
a2[i] = a1[i];
a3[i] = a2[i];
a4[i] = a3[i];
a5[i] = a1[i];
}
int begin1 = clock();
InsertSort(a1, N);
int end1 = clock();
int begin2 = clock();
ShellSort(a2, N);
int end2 = clock();
int begin3 = clock();
BubbleSort(a3, N);
int end3 = clock();
int begin4 = clock();
HeapSort(a4, N);
int end4 = clock();
int begin5 = clock();
SelectSort(a5, N);
int end5 = clock();
printf("InsertSort:%d\n", end1 - begin1);
printf("ShellSort:%d\n", end2 - begin2);
printf("BubbleSort:%d\n", end3 - begin3);
printf("HeapSort:%d\n", end4 - begin4);
printf("SelectSort:%d\n", end5 - begin5);
}
int main()
{
TestOP();
return 0;
}