链式二叉树的实现及遍历(C语言版)

目录

1 基本概念

1.1 树的概念

1.2 二叉树的链式表示

1.2.1 "左孩子右兄弟"表示法

1.2.2 "左右子树"表示法

1.2.3 手动构建一棵树

2 树的遍历

2.1 前序遍历/先序遍历

2.2 中序遍历

2.3 后序遍历

2.4 层序遍历

2.4.1 算法思想

​编辑 2.4.2 带头尾指针链式队列的代码

3  其他接口函数

3.1 求树的节点个数

3.2 求叶子节点个数

3.3 二叉树的销毁

3.4  遍历寻找二叉树中值为x的节点 

---

1 基本概念

---

1.1 树的概念

⭕树是一种非线性的数据结构

⭕树的根结点没有前驱节点，根节点可以指向任意多个子节点(N叉树)

⭕树形结构中，子树之间不能有交集，否则就是图

---

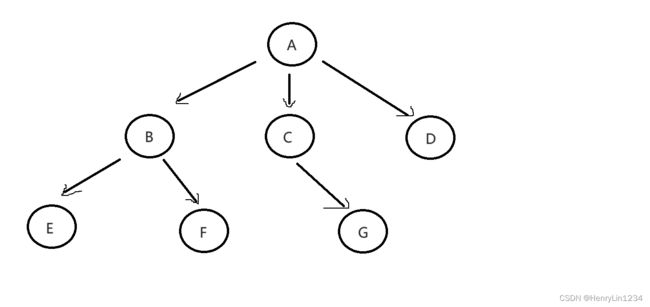
⭕度：一个节点含有的子树的个数。例如二叉树的根节点的度为2，上图A节点的度为3

⭕树的度：一棵树中最大的节点的度。如二叉树的度就是其根节点的度，上图树的度为3

⭕树的高度或深度：树中节点的最大层次。如上图树的高度为3

⭕叶子节点或终端节点：度为0的节点。如上图的E F G均为叶子节点

---

1.2 二叉树的链式表示

---

1.2.1 "左孩子右兄弟"表示法

---

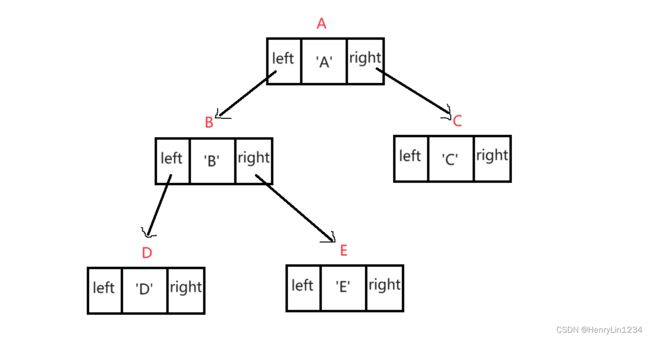
1.2.2 "左右子树"表示法

⭕问：为什么不叫“左右孩子”表示法呢？

答：结构体内的left指针和right指针的确指向根的左右孩子节点，但是以整体的思想，左右孩子节点又是左子树和右子树的根节点，以“左右子树”命名有利于帮助我们理解二叉树的一系列递归问题。

⭕在现阶段，我们运用“左右子树”表示法更多一些。  

---

1.2.3 手动构建一棵树

---

typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;


    BTNode* A = (BTNode*)malloc(sizeof(BTNode));
	A->data = 'A';
	A->left = NULL;
	A->right = NULL;

	BTNode* B = (BTNode*)malloc(sizeof(BTNode));
	B->data = 'B';
	B->left = NULL;
	B->right = NULL;

	BTNode* C = (BTNode*)malloc(sizeof(BTNode));
	C->data = 'C';
	C->left = NULL;
	C->right = NULL;

	BTNode* D = (BTNode*)malloc(sizeof(BTNode));
	D->data = 'D';
	D->left = NULL;
	D->right = NULL;

	BTNode* E = (BTNode*)malloc(sizeof(BTNode));
	E->data = 'E';
	E->left = NULL;
	E->right = NULL;

	A->left = B, A->right = C;
	B->left = D, B->right = E;

---

2 树的遍历

---

2.1 前序遍历/先序遍历

前序遍历/先序遍历：又叫深度优先遍历，根->左子树->右子树

问：下图的树先序遍历的输出结果是什么？

---

很多教材上的答案是ABDEC，但其实对于初学者特别不友好，初学者可能看得懂这个答案，但是到中序和后序遍历就看不懂了，所以我复现一下遍历过程：

所以教材上的答案多半忽略了对空指针的访问输出，这其实对我们理解遍历是不利的。

上面这个动图是我自己手动制作的，如果想要自己也动起手来，可以访问下面这篇我的博客：

http://t.csdn.cn/JZpjQ

---

void PrevOrder(BTNode* root)
{
	if (root == NULL)
    {
        printf("(null) ");
		return;
    }
	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}

---

2.2 中序遍历

中序遍历：左子树->根->右子树

 问：下图的树中序遍历的输出结果是什么？

---

建议大家花个几分钟时间自己做一下，空指针访问也表示出来，有利于帮助我们理解递归。

void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("(null) ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}

答案：

 

---

2.3 后序遍历

后序遍历：左子树->右子树->根

问：下图的树中序遍历的输出结果是什么？

---

动图就不制作了，大家可以验证答案后自己动手制作动图。

void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("(null) ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}

---

2.4 层序遍历

层序遍历：一层一层节点遍历，又叫广度优先遍历

层序遍历本身直观，实现起来比较麻烦，思想蕴含在代码里。

2.4.1 算法思想

①利用先进先出的队列，第一次先入二叉树的根节点到队列中，然后入不为空的子节点，pop掉根节点，如果树的根节点都为空，那么就没有入的必要了。

if (root)
	QuePush(&q, root);

if(root->left)
    QuePush(&q,root->left);
if(root->right)
    QuePush(&q,root->right);

QuePop(&q);

②第二次入原来根节点的左子树根节点的左右非空节点，然后pop掉该节点。

③第三次入原来根节点的右子树根节点的左右非空节点，然后pop掉该节点。

④依次循环，直到队列为空。那么只要队列不为空，循环就继续。

void LevelOrder(BTNode* root)
{
	Que q;
	QueInit(&q);

    if(root)
	    QuePush(&q,root);
	while (!QueEmpty(&q))
	{
		BTNode* front = QueFront(&q);
		QuePop(&q);
		printf("%c ", front->data);
		
		if (front->left)
			QuePush(&q, front->left);
		if (front->right)
			QuePush(&q, front->right);
	}
}

 2.4.2 带头尾指针链式队列的代码

Queue.h

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include
#include

struct BinaryTreeNode;
typedef struct BinaryTreeNode* QDataType;

typedef struct QueueNode
{
	struct QueueNode* next;
	QDataType data;
}QNode;

typedef struct Queue
{
	QNode* head;
	QNode* tail;
	int size;
}Que;

void QueInit(Que* pq);
void QueDestroy(Que* pq);
void QuePush(Que* pq, QDataType x);
void QuePop(Que* pq);
QDataType QueFront(Que* pq);
QDataType QueBack(Que* pq);
bool QueEmpty(Que* pq);
int QueSize(Que* pq);

Queue.c

#include"Queue.h"
void QueInit(Que* pq)
{
	assert(pq);
	pq->head = pq->tail = NULL;
	pq->size = 0;
}
void QueDestroy(Que* pq)
{
	assert(pq);

	QNode* cur = pq->head;
	while (cur)
	{
		QNode* next = cur->next;
		free(cur);
		cur = next;
	}
	pq->head = pq->tail = NULL;
}
void QuePush(Que* pq, QDataType x)
{
	assert(pq);
	QNode* newnode = (QNode*)malloc(sizeof(QNode));
	newnode->next = NULL;
	newnode->data = x;

	if (newnode == NULL)
	{
		perror("malloc fail\n");
		exit(-1);
	}
	if (pq->head == NULL)
	{
		pq->head = pq->tail = newnode;
	}
	else
	{
		pq->tail->next = newnode;
		pq->tail = newnode;
	}
	pq->size++;
}
void QuePop(Que* pq)
{
	assert(pq);
	assert(!QueEmpty(pq));
	//单结点
	if (pq->head->next == NULL)
	{
		free(pq->head);
		pq->tail = pq->head = NULL;
	}
	else
	{
		QNode* next = pq->head->next;
		free(pq->head);
		pq->head = next;
	}
	pq->size--;
}
QDataType QueFront(Que* pq)
{
	assert(pq);
	assert(!QueEmpty(pq));

	return pq->head->data;
}
QDataType QueBack(Que* pq)
{
	assert(pq);
	assert(!QueEmpty(pq));

	return pq->tail->data;
}
bool QueEmpty(Que* pq)
{
	assert(pq);
	return pq->head == NULL;
}
int QueSize(Que* pq)
{
	assert(pq);
	return pq->size;
}

---

3  其他接口函数

---

3.1 求树的节点个数

算法思想：

①左子树的节点个数+根本身+右子树的节点个数

②根为空就返回

int TreeSize(BTNode* root)
{
	if(root==NULL)
        return 0;
    return 1+TreeSize(root->left)+TreeSize(root->right);
}

---

3.2 求叶子节点个数

算法思想：

①什么是叶子：度为0，即左指针和右指针为空

②遇到空则返回

③一棵树的叶子节点=左子树的叶子节点+右子树的叶子节点

int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}

---

3.3 二叉树的销毁

问：为什么选择后序遍历销毁二叉树？而不是前序和中序遍历？

答：前序遍历会导致访问不到根左子树和右子树，引发对空指针的访问；中序遍历会导致访问不到根的右子树，引发对空指针的访问；只有后序遍历才能保证销毁根的左子树和右子树后再销毁根。

void TreeDestroy(BTNode** proot)
{
	if (*(proot) == NULL)
		return;
	TreeDestroy((*proot)->left);
	TreeDestroy((*proot)->right);
	free(*proot);
    *proot=NULL;
}

---

3.4  遍历寻找二叉树中值为x的节点 

BTNode* TreeFind(BTNode* root, BTDataType x) 
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;

	BTNode* ret=TreeFind(root->left, x);
	if (ret != NULL)
		return ret;
	ret=TreeFind(root->right, x);
	if (ret != NULL)
		return ret;

	return NULL;
}

---

 4 二叉树代码

BinaryTree.h

#pragma once
#define _CRT_SECURE_NO_WARNINGS 1
#include
#include
#include


typedef char BTDataType;
typedef struct BinaryTreeNode
{
	struct BinaryTreeNode* left;
	struct BinaryTreeNode* right;
	BTDataType data;
}BTNode;
BTNode* BuyNode(BTDataType x);
//前序遍历：根 左子树 右子树
void PrevOrder(BTNode* root);
//中序遍历：左子树 根 右子树
void InOrder(BTNode* root);
//后序遍历：左子树 右子树 根
void PostOrder(BTNode* root);
int TreeSize(BTNode* root);
int TreeLeafSize(BTNode* root);
void TreeDestroy(BTNode** proot);
BTNode* TreeFind(BTNode* root, BTDataType x);
//层序遍历
void LevelOrder(BTNode* root);

 BinaryTree.c

#include"BinaryTree.h"
#include"Queue.h"

BTNode* BuyNode(BTDataType x)
{
	BTNode* root = (BTNode*)malloc(sizeof(BTNode));
	root->data = x;
	root->left = root->right = NULL;
	return root;
}
//前序遍历：根 左子树 右子树
void PrevOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("(null) ");
		return;
	}

	printf("%c ", root->data);
	PrevOrder(root->left);
	PrevOrder(root->right);
}
//中序遍历：左子树 根 右子树
void InOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("(null) ");
		return;
	}
	InOrder(root->left);
	printf("%c ", root->data);
	InOrder(root->right);
}
//后序遍历：左子树 右子树 根
void PostOrder(BTNode* root)
{
	if (root == NULL)
	{
		printf("(null) ");
		return;
	}
	PostOrder(root->left);
	PostOrder(root->right);
	printf("%c ", root->data);
}
int TreeSize(BTNode* root)
{
	return root == NULL ? 0 : 1 + TreeSize2(root->left) + TreeSize2(root->right);
}
int TreeLeafSize(BTNode* root)
{
	if (root == NULL)
		return 0;
	if (root->left == NULL && root->right == NULL)
		return 1;
	return TreeLeafSize(root->left) + TreeLeafSize(root->right);
}
//层序遍历
void LevelOrder(BTNode* root)
{
	Que q;
	QueInit(&q);
	if(root)
		QuePush(&q,root);//队列每一个元素的类型都是BTNode*
	while (!QueEmpty(&q))
	{
		BTNode* front = QueFront(&q);
		QuePop(&q);
		printf("%c ", front->data);
		
		if (front->left)
			QuePush(&q, front->left);
		if (front->right)
			QuePush(&q, front->right);
	}
}
void TreeDestroy(BTNode** proot)
{
	if (*proot == NULL)
		return;
	TreeDestroy((*proot)->left);
	TreeDestroy((*proot)->right);
	free((*proot));
	*proot = NULL;
}
BTNode* TreeFind(BTNode* root, BTDataType x) 
{
	if (root == NULL)
		return NULL;
	if (root->data == x)
		return root;
	BTNode* ret=TreeFind(root->left, x);
	if (ret != NULL)
		return ret;
	ret=TreeFind(root->right, x);
	if (ret != NULL)
		return ret;
	return NULL;
}