【强化学习-01】强化学习基本概念

本笔记整理自 (作者: Shusen Wang):
https://www.bilibili.com/video/BV1rv41167yx?from=search&seid=18272266068137655483&spm_id_from=333.337.0.0

概率基本概念

概率密度函数

probability density function

continuous distribution

Discrete distribution

概率密度加和为1

概率分布的期望

随机抽样

这里的random sampling在强化学习中使用的非常频繁。比如在选择下一个action的时候以及下一阶段的state的时候，就会经常用到random sampling.

强化学习基本概念

State, action

State $s$: 当前所处的状态，上图中就是这一帧的画面(frame)，包括马里奥的位置，金币的位置，敌人的位置等
Action $a$：agent(智能体)可以选择的动作。action $\in \{\text{left, right, up}\}$,其实这里还应该有个stay，stay也是一个动作
Agent：发出动作的主体，动作是由谁做的谁就是agent

Policy $\pi$

policy的意思就是根据观测到的状态。做出决策来控制agent运动
在数学上，Policy $\pi$是一个概率密度函数 ，满足

1. $\pi (s,a)\in [0,1]$
2. $\pi (a|s)=\mathbb{P}(A=a|S=s)$

注意：大写表示是随机变量(random variable)，小写表示观测值(observation)
给定状态$S=s$,下一步的具体动作$a$是随机抽样得到的，要有随机性

Reward

reward通常需要我们自己来定义，reward定义的好坏非常影响强化学习的结果

注意，针对马里奥的游戏：尽量要把打赢游戏的奖励给的高一些，这样就不会总是吃金币。

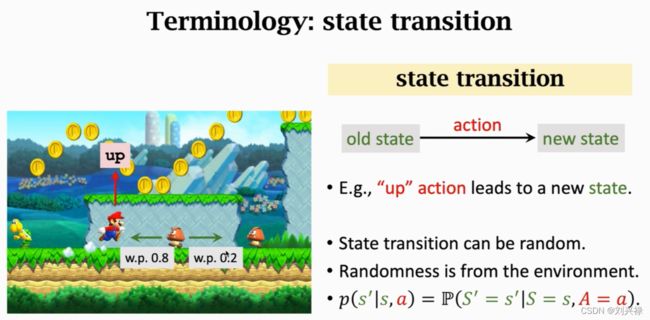
State transition

状态转移：当前状态下，mario采取一个动作，游戏就会给一个新的状态。比如mario跳一下，游戏的下一个状态就不一样了
状态转移可以是确定的，也可以是随机的
状态转移的随机性是从环境(environment)中来的。
下图：goomba的移动概率是向左0.8，往右移动的概率为0.2
但是对于玩家而言，我们不知道goomba向左或者向右的概率，这个概率只有系统知道。

状态转移函数
$$\begin{array}{r}p(s^{\prime }|s,a)=\mathbb{P}(S^{\prime }=s^{\prime }|S=s,A=a)\end{array}$$

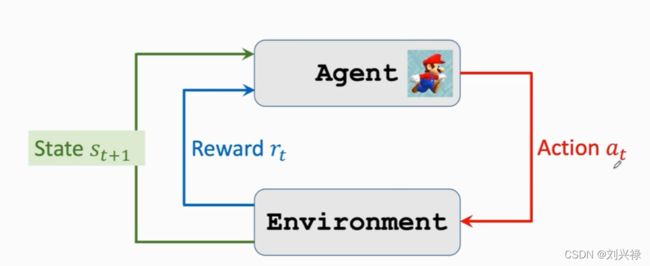
Agent environment interaction

这里的environment就是游戏
State就是环境告诉我们的，可以看成是当前的游戏画面

agent在状态$s_t$的情况下，做出动作$a_t$ (left, right, up)，然后environment给出下一时刻的状态$s_{t+1}$，并且给出相应的reward $r_t$.

强化学习中的随机性

1. Action的随机性：给定状态$s$，下一个阶段的动作，是根据Policy $\pi$ (这是一个概率密度函数)抽样得来的。
   
2. 状态转移的随机性：环境根据当前状态$s$和可选的action，用状态转移函数$p$计算出每个动作的概率，然后用随机抽样来决定下一步的action。
   

Play the game using AI

Rewards and returns

$U_t$跟未来的所有action和state都有关，因此是随机的。

Value functions

Action-Value function

Action-Value function:
$$Q_{\pi }(s_t,a_t)=\mathbb{E}[U_t|S_t=s_t,A_t=a_t]$$
$Q_{\pi }(s_t,a_t)$是跟策略函数$\pi$以及状态$s$和动作$s$有关的，给定Policy $\pi$，State $s$, Action $a$，我们可以进行积分，获得$Q_{\pi }(s_t,a_t)$。这里需要注意，实际上$Q_{\pi }(s_t,a_t)$也是跟$s_{t+1},s_{t+2},\cdots$以及$a_{t+1},a_{t+2},\cdots$ 有关的，这个可以根据$U_t$的定义可得。但是由于积分将这些全部消除，就只剩下了观测值$s_t$和$a_t$。如果$\pi$不一样，积分得到的$Q_{\pi }(s_t,a_t)$也不一样。

Optimal action-Value function

最优动作价值函数，Optimal action-Value function与$\pi$无关，因为$\pi$已经被$\max$给消除了。
Optimal action-Value function $Q^{\ast }(s_t,a_t)$可以用来对动作作评价。
有了$Q^{\ast }(s_t,a_t)$，agent就可以利用$Q^{\ast }(s_t,a_t)$来做动作了。

另外，Q值是对未来奖励总和的期望。

State-Value function

$V_{\pi }(s_t)={\mathbb{E}}_A[Q_{\pi }(s_t,A)]$: 在given state $s_t$之后，将下一步可以做的动作$A$作为随机变量，对$A$求积分，将$A$消掉

上面对$A$求期望，也就是${\mathbb{E}}_A[Q_{\pi }(s_t,A)]$的式子中，随机变量$A$是服从分布$A\sim \pi (\cdot |s_t)$的，也就是given state $s_t$。如果$a$是离散的，则可以将期望写成连加的形式

如说是连续的action，则需要进行积分。

Understanding the value functions

• Action-value function: $Q_{\pi }(s_t,a_t)$是给动作$a_t$进行打分，也就是agent在状态$s_t$的时候做出动作$a_t$是否明智
• State-value funcrion:
  

Using AI to play games

How does AI controls the agent

• Policy based learning: 第一种方法是学习policy。已知policy $\pi (a|s)$，我们就可以given state，然后根据概率分布，对action $a$进行随机抽样，得到$a_t$，最后agent执行动作$a_t$。
• Value based learning:另外一种方法是学习最优动作价值函数$Q^{\ast }(s_t,a_t)$。然后agent可以根据$$a_t={\text{argmax}}_a{Q}^{\ast }(s_t,a)$$，执行下一步的动作，因为$Q$值是对未来奖励的期望。
  

以上两种方法都可行，也就是强化学习中也么是学习$\pi (\cdot |s_t)$函数或者$Q^{\ast }(s_t,a_t)$函数，只要学到两者之一即可。

例子

总结

这里总结一下

• Value based learning:算法temporal difference
• Policy based learning:算法policy gradient

经典论文

Q-learning:
@article{watkins1992q,
title={Q-learning},
author={Watkins, Christopher JCH and Dayan, Peter},
journal={Machine learning},
volume={8},
number={3-4},
pages={279–292},
year={1992},
publisher={Springer}
}