【深度学习】计算机视觉（13）——模型评价及结果记录

1 Tensorboard怎么解读？

因为意识到tensorboard的使用远不止画个图放个图片那么简单，所以这里总结一些关键知识的笔记。由于时间问题，我先学习目前使用最多的功能，大部分源码都包含summary的具体使用，基本不需要自己修改，因此tensorboard的解读作为目前学习的核心，所以本文的知识结构可能不是很完整，以后的学习中再慢慢调整。

ps：便于更直观的理解，文中给出的代码大多是我学习时直接从项目源码那里复制过来的，如果没有特殊说明，文中出现的路径、字符串等都是项目特定内容，不影响学习也不必深究其含义。

1.1 histogram直方图

1.1.1 概念

通过tf.summary.histogram生成某一张量tensor的直方图，在TensorBoard直方图仪表板上显示。直方图是显示张量在不同时间点的，通过直方图显示某些值的分布随时间变化的情况。

如何理解“随时间”变化？按照初学时的理解，在训练网络的过程中，数据肯定是随着迭代次数的增加慢慢保存更新的，比如loss曲线的生成，横坐标一定与迭代次数正相关。通过阅读代码我了解到，我们设置了每隔一定的时间，保存一次summary，也就是说实际上迭代的次数体现在时间的变化。

The time interval for saving tensorflow summaries

1.1.2 数据解读

先抛开时间不谈，从分布情况的角度看，tf.summary.histogram()将输入的一个任意大小和形状的张量压缩成一个由宽度和数量组成的直方图数据结构。
举个例子便于理解，假设输入的数据为 [0.5, 1.1, 1.3, 2.2, 2.9, 2.5]，直方图将横坐标分成三个区间，分别为0-1、1-2、2-3，而纵坐标表示在每个区间内的元素的数量。实际上tensor读取的图片像素是有维度要求的，而且划分区间也有一定的规则，那么模拟一下真实情况，还是用上面的数据构造一个RGB图片：

import tensorflow as tf
from torchvision import transforms
from torch.utils.tensorboard import SummaryWriter
import numpy as np

writer = SummaryWriter("logs")

# width = 6 and height = 2
img_row = [0.5, 1.1, 1.3, 2.2, 2.9, 2.5]
img_r = [img_row, img_row]
img_g = [img_row, img_row]
img_b = [img_row, img_row]
img = [img_r, img_g, img_b]

ans = np.array(img, dtype='float')

to_tensor = transforms.ToTensor()
ans = to_tensor(ans)

writer.add_histogram("test histogram sample of img", ans)

writer.close()

得到的直方图如下：

其中x和y的对应关系为：

x = ?	y = ?
0.54	6.00
0.62	0.00
0.94	0.00
1.02	3.03
1.1	2.97
1.18	0.00
1.26	3.89
1.34	2.11
1.42	0.00
2.06	0.00
2.14	0.477
2.22	2.22
2.3	2.22
2.38	2.12
2.46	2.02
2.54	2.02
2.62	0.933
2.7	0.00
2.78	0.00
2.86	0.00

说明：虽然直方图看起来是连续的，但是鼠标移动时只显示这这几对数据，每组数据之间直线连接。

1.1.3 数据计算

显示在tensorboard时，默认将数据分为30个区间，每个区间的长度为(max-min)/30，即(2.9-05)/30=0.08。而每组x_i取区间的中点，比如第一组区间为[0.5, 0.58]，则x₁=0.54，同理第二组x₂=0.62。

但是显示和实际数值是有区别的，实际上，区间并不是等分的，而是从0开始，区间长度是首项为0.1×10^-12、公比为1.1的等比数列，且最后一个区间的长度需要进行截取，满足右端点经截取后保证不超过max。它使用指数分布来产生区间，越接近零区间分得越密，越大的数区间的长度越宽。我们将这些区间称为bin。

区间划分的规则清楚后学习实际的数据(x’_i, y’_i)与显示数据(x_j, y_j)之间的对应关系。公式为：

比如显示区间[2.50, 2.58]对应的中点x=2.54。
计算实际区间，根据等比数列可知，第300个区间为[2.3791, 2.617]（经四舍五入后），"交集长度"为2.58-2.50=0.08，"区间大小"为2.617-2.3791=0.2379。因为在数列[0.5, 1.1, 1.3, 2.2, 2.9, 2.5]中只有2.5在[2.3791, 2.617]范围内，而且我构造的图片是6个这样的数列组成的张量，所以"区间所含元素个数"为1×6=6。
则当x=2.54时，y=0.08÷0.2379×6=2.0176，对照上表，2.0176≈2.02。

附：求实际区间按照等比数列求和公式S_n，已知首项和公比，第n个区间的端点为[S_n-1, S_n]。

验证1：显示数据为(1.02, 3.03)，对应实际区间第291个区间[1.009, 1.1099]，数据正确。

验证2：显示数据为(2.14, 0.477)，对应实际区间第298个区间[1.9662, 2.1628]或第299个区间[2.1628, 2.3791]，因为第298个区间里没有数据，所以对照第299个区间，数据正确。

1.1.4 OVERLAY和OFFSET

上一小节没有引入时间的概念，数据范围和数量已经构成了二维图像，那么随时间的变化如何表示呢？直方图有两种模式：OVERLAY和OFFSET。

OVERLAY

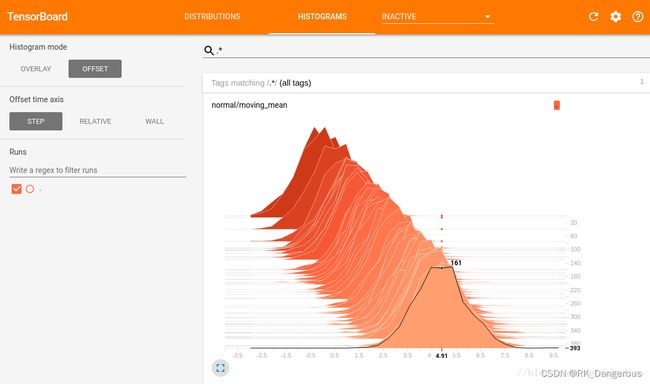
横轴表示bin值，纵轴表示数量，每个切片显示一个直方图，切片按步骤（步数或时间）排列。旧的切片较暗，新的切片颜色较浅。如图，可以看到在第393步时，以4.91为中心的bin中有161个元素。

另外，直方图切片并不总是按步数或时间均匀分布，而是通过水塘抽样/reservoir sampling来抽取所有直方图的一个子集，以节省内存．

OVERLAY

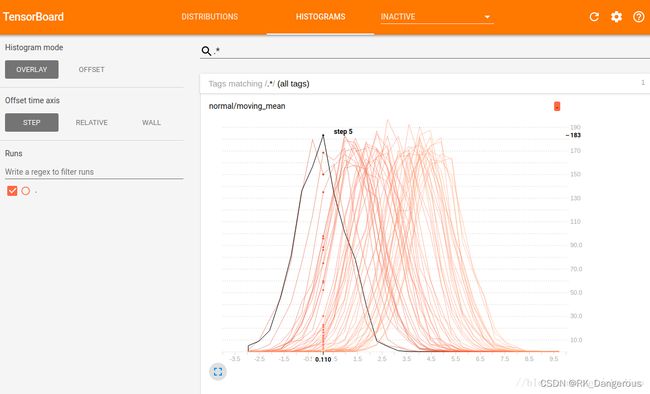
同样，横轴表示bin值，纵轴表示数量。但是OVERLAY模式下各个直方图切片不再展开，而是全部绘制在相同的y轴上，不同的线表示不同的步骤（步数或时间）。如图，可以看到在第5步时，以0.11为中心的bin中有183个元素。

OVERLAY模式用于直接比较不同直方图的计数．

1.1.5 应用

利用tf.summary.histogram可视化梯度、权重或特定层的输出分布，可传入的张量包括但不限于：网络输出特征（act_summary)、训练结果（score_summary)、需要训练的变量（train_summary)。根据代码为不同直方图设置标签，可生成多个直方图。

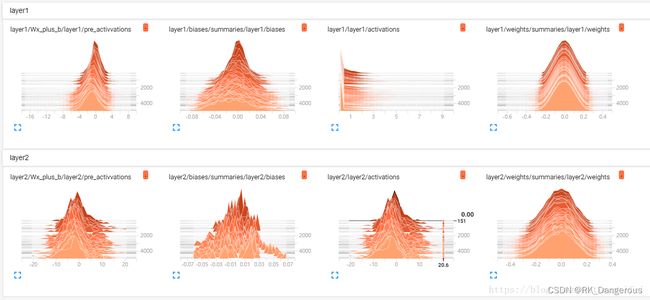
act_summary

tf.summary.histogram('ACT/' + tensor.op.name + '/activations', tensor)

传入的张量tensor = [net, rpn]，其中net.shape = [1, w/16, h/16, 512]，rpn.shape = [1, w/16, h/16, 512]，显示神经网络两次特征的输出net、rpn的特征值分布。

score_summary

tf.summary.histogram('SCORE/' + tensor.op.name + '/' + key + '/scores', tensor)

传入的张量生成多个不同功能的分布直方图，例如网络输出、预测分数、预测概率、预测偏移、预测框坐标等。

train_summary

tf.summary.histogram('TRAIN/' + var.op.name, var)

传入的张量包括需要训练的变量的值。

var.op.name是指每个变量在创立时的操作的名字，也即为变量申请内存时的那个操作的名字。而var.name是Tensor名字，Tensor是操作的输出，也就是在创立变量的这个操作的输出就是所创立的变量。

我是这样理解的，python在使用变量的时候像指针一样指来指去的，最外面的那个是var.name，最里面的那个是var.op.name。

参考来源

TensorBoardX histogram查看说明
等比数列的前n项和公式是什么
TensorFlow学习Program1——4.TensorBoard可视化数据流图
TensorFlow学习－－tf.summary.histogram与直方图仪表板/tensorboard_histograms
【Tensorflow_DL_Note17】TensorFlow可视化学习4_tf.summary模块的详解
Tensorfow基础知识点&操作
Tensorflow-tf.nn.zero_fraction()详解