基础排序算法

插入排序（insertion sort）

插入排序每次循环将一个元素放置在适当的位置。像抓牌一样。手里的排是有序的，新拿一张牌，与手里的牌进行比较将其放在合适的位置。

插入排序要将待排序的数据分成两部分，一部分有序，另一部分待排序。默认任务数组第一个元素是有序的，然后依次取剩下的元素插入有序部分合适的位置。

算法实现

   public static void sort(int[] arr){
        int len = arr.length;
        /**
         * 将数组分成两部分
         * [0] 已排序  & [1,2,3...length-1] 待排序
         * 第一层循环将待排序元素逐个拿出与已排序部分进行插入排序
         */
        for (int i = 1; i < len; i++) {
            //先把当前循环要排序的元素从数组拿出来，空出来一个数组位置
            int val = arr[i];
            // j 当前插入位置指针
            int j = i-1;
            for (; j > 0 ; j--) {
                if(val < arr[j]){//当前插入指针位置元素比当前待排序值大，将当前位置元素后移
                    arr[j+1] = arr[j];
                }else {//当前插入指针位置元素比当前值小，好了，就应该在这里插入，插入到指针位置的后面 j+1
                    break;
                }
            }
            arr[j+1] = val;  
        }
    }

实际数据分析：

例 {2,6,5,4,8,7}

排序过程： 默认数组第一个位置2已排好，从6开始插入排序。

第一次：把6拿出来，然后6的位置可以被覆盖。

内循环：插入指针为6的下标往前一个，第一次拿出2进行比较。6 >2 。6要插入2的后面，跳出循环

第二次：拿出5 内循环：插入指针为5的下标-1， 第一次拿出6，5<6。不能在这里插入，插入点还得往前移动。这个时候要把6的位置后移一位， 因为5要插入6前面，但是现在没有位置。正好5被拿出来了，5的位置现在可以被使用。 经过一次内循环插入指针移动到了2位置，6向后移动一位。这时数组变成{2,6,6,4,8,7}。内循环第二次拿出2，5>2, ok找到插入点了，跳出内循环，5插入2的后面也就是原来6的位置。 将5放入插入位置，这时候数组变成了{2,5,6,4,8,7}。结束5的排序

第三次依次操作。

插入排序的插入理解就是将待排序的当前元素插入到有序部分合适的位置。比较前先将当前元素拿出来，在比较的过程中，如果当前元素的排序位置没找到，不需要进行交换。只需要将当前有序部分的比较元素后移一位，让出插入位置。进行下一次比较依次类推。直到找到插入位置，将当前元素放入该位置。

插入排序最好情况时间复杂度是O(n)。已经是有序的了，只一遍外循环即可。最坏情况是O(n^2)。排序算法是稳定的，因为不存在交换。也不需要开辟额外的空间。

希尔排序

希尔排序是插入排序的变种。我们知道插入排序的时间复杂度是O(n^2)。一次只能对一个元素位进行排序，并且遇到较小值在数组后部时，要进行多次比较移位才能将其放置合适位置。希尔排序能提高一定的平均排序效率。但是实际中使用的可能也不太多。

排序原理

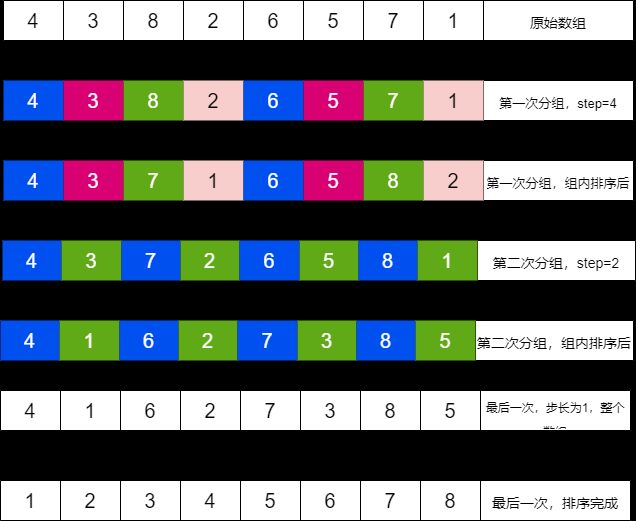
每次按特定步长（step）将待排序分成若干组，然后每组内进行插入排序。步长取值通常为元素长度 length/2,length/(2*2)…1。最后一次步长变成1演变成完全插入排序。

代码实现

    static void sort(int[] arr){
        int len = arr.length;
        //step为步长，分组元素间的间隔
        for (int step = len/2; step >0; step /=2) {
            //每一组进行插入排序，
            for (int i = step; i < len; i++) {//外层循环每+1表示新一组元素
                int temp = arr[i];//待插入元素先拿出来
                int p = i;//当前插入指针，p-step是当前组已排序好的部分，依次拿出与当前值进行比较
                for (; p >= step ; p -= step) {//每次取同组元素，同组元素的间隔是step值
                    if(arr[p - step] > temp){
                        arr[p] = arr[p - step];
                    }else{//找到插入位置
                        break;
                    }
                }
                arr[p] = temp;//将元素插入当前位置
            }
        }
    }

实例分析：

冒泡排序（Bubble sort）

排序算法像冒泡一样每次遍历通过比较找到待排序元素中最大的一个，然后上浮到已排序部分。

代码实现

    static void sort(int[] arr){
        int len = arr.length;
        for (int i = 0; i < len-1; i++) {
			//len-i个元素已排好，所以内循环次数是len-i-1
            for (int j = 0; j < len-i-1; j++) {
               /**前面元素比后面元素大就进行交换，大元素后移。这样内循环结束后就找到了本次所有参与循环元素的最大值，并放到最后。
				*/
                if(arr[j] > arr[j+1]){
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                }
            }
            System.out.println(Arrays.toString(arr));;
        }
    }

优化：每次冒泡排序内循环记录是否有交换发生。如果没有交换发生，则整个数组已经是有序的了。仔细理解下这句话。代码实现

  static void sort(int[] arr){
        int len = arr.length;
        for (int i = 0; i < len-1; i++) {
            boolean swap = false;
            for (int j = 0; j < len-i-1; j++) {
                if(arr[j] > arr[j+1]){
                    int tmp = arr[j];
                    arr[j] = arr[j+1];
                    arr[j+1] = tmp;
                    swap = true;
                }
            }
            if(!swap) break;//没有交换发生，跳出循环
            System.out.println(Arrays.toString(arr));;
        }
    }

冒泡排序时间复杂度和插入排序一样最好都是O(n),最后是O(n^2)。

选择排序

排序思想

每次从未排序的部分选择最小（或最大）的元素，放到已排序部分的末尾，直到整个数组排序完成。

代码实现

    public static void sort(int[] arr){
        int len = arr.length;
        for (int i = 0; i < len-1; i++) {
            int p = i;//记录最小位置指针，默认记录为本次循环第一个元素位置
            for (int j = i+1; j < len ; j++) {
                //如果当前数比原来标记最小数小，记录当前位置为最小数指针
                if( arr[j] < arr[p] ) p = j;
            }
            //找到本次最小数指针，如果指针不是第一个元素，将第一个元素与最小值元素进行位置交换
            if(p != i){
                int temp = arr[i];
                arr[i] = arr[p];
                arr[p] = temp;
            }
        }
    }

选择排序存在元素跨距离交换，不稳定，时间复杂度O(n^2)。理解起来和冒泡排序很像。不过中间少了很多交换。

归并排序

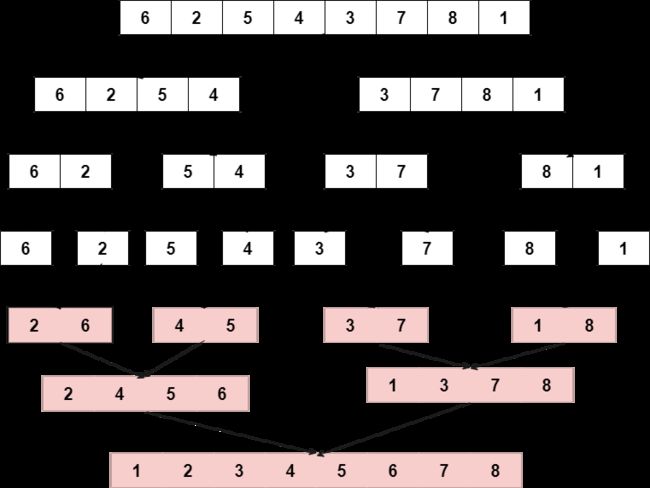
归并排序将待排序数组每次进行二分，直到每一组分成1个元素，则顺序也就出来了。然后再依次进行合并操作最后生成一个有序的操作。

分比较好操作每次数组进行二分即可。合就是要将分的两部分A、B依次拿出一个值（两部分当前最小的值，中间需要比较是取A部分的还是取B部分）来组合起来。因为分后的两部分已经是有序的了，所以最后两部分所有元素取完合起来的整个也是有序的。

排序过程图：

代码实现：

    public static void sort(int[] arr,int start,int end){
        //元素开始和结束位置相等，不能再分了，结束
        if(start >= end) return;
        //将要排序的数组进行平分
        int mid = (start + end) /2;
        sort(arr,start,mid);//前半部分进行排序
        sort(arr,mid+1,end);//后半部分进行排序
        //合并本次排序结果
        merge(arr,start,mid,end);
    }
    /**
     * 排序两部分 {start,mid} ,{mid+1,end} 都已排序完成，合并两部分
     * 合并过程：
     */
    public static void merge(int[] arr,int start,int mid,int end){
        int p1 = start;//左半部分当前下标
        int p2 = mid+1;//右半部分当前下标
        int index = start;//temp临时数组存储下标，从start开始
        /**
         * 合并已排序的两部分
         * 每次从左边部分和右边部分各拿出一个元素进行比较，小的放入数组中，
         * 然后从小的所在部分再拿出一个与上一次大的元素进行比较
         */
        while (p1 <= mid && p2 <= end){
            if(arr[p1] < arr[p2]){
                temp[index++] = arr[p1++];
            }else{
                temp[index++] = arr[p2++];
            }
        }
        /**
         * while 循环结束表示至少数组两部分有一部分取完，但是不一定两部分都取完。
         * 最后将左边部分和右边部分可能剩余的部分放入临时数组中。
         */
        while (p1 <= mid){
            temp[index++] = arr[p1++];
        }
        while (p2 <= end){
            temp[index++] = arr[p2++];
        }
        /**
         * 执行到这里 temp{start,end} 部分都已排好序，
         * 将temp{start,end}部分放入原数组中。
         */
        for (int i = start; i <= end; i++) {
            arr[i] = temp[i];
        }

    }

快速排序

算法思想：

快速排序取数组第一个元素作为基准数，然后将剩余元素与基准数进行比较，比基准数大的放在基准数左边，小的放在基准数右边，基准数在中间。然后再将基准数两个子结果进行递归按上面取基准数排序。最后整个数组变为有序的。

代码实现

    public static void sort(int arr[],int left ,int right){
        if(left >= right) return;

        int p1 = left;
        int p2 = right;
        int val = arr[left];//取数组第一个元素作为基准数
        while ( p1 < p2){
            /**
             * 从右往左找比基准数小的数
             * 找到后将其放到p1指针位置
             */
            while (p2 > p1 && arr[p2] >= val)
                p2--;
            arr[p1] = arr[p2];

            /**
             * 从左往左找找到比基准数大的数
             * 找到后将其放到p2指针位置，这个时候p2经过上面的查找已经被放到p1位置，可以覆盖
             */
            while (p1 < p2 && arr[p1] <= val)
                p1++;
            arr[p2] = arr[p1];
            //继续交叉查找
        }
        //找到中间位置了（左边的数都小于基准数，右边的数都大于基准数），将基准数放到该位置
        arr[p2] = val;
        //递归的将数组以基准数为分界点分成两部分，各自进行快速排序
        sort(arr,left,p2);
        sort(arr,p2+1,right);
    }

排序过程分析

首先取数组的第一个元素作为基准数，然后这样数组第一个位置就可以覆盖，然后从数组的末尾往前找比基准数小的数，如果找到就将其移动到原基准数的位置。这个时候刚被移动的元素位置又空出来了，这个时候在从前往后找比基准数大的，找到后在将其放到该位置。循环往复的进行以上操作。直到从后往前找的指针和从前往后找的指针位置相等，表示整个数组已经找完，将基准数放置在该位置。最后数组被分成了：[{小于基准数}{基准数}{大于基准数}]三部分。然后再对小于基准数部分和大于基准数部分进行递归的上面排序过程。直到被分元素只有一个，排序完成。

从上面的分析过程可以看出，快速排序会进行大量的跨距离移位操作，是不稳定的。平均时间复杂度是O(n*logn)

总结

排序算法	时间复杂度	空间复杂度	适用场景
冒泡排序	最好情况：O(n) 最坏情况：O(n^2) 平均情况：O(n^2)	O(1)	小型数据集或部分有序数据集
插入排序	最好情况：O(n) ； 最坏情况：O(n^2) ； 平均情况：O(n^2)	O(1)	小型数据集或部分有序数据集
选择排序	始终为O(n^2)	O(1)	小型数据集
快速排序	最好情况：O(nlogn) ； 最坏情况：O(n^2) ；平均情况：O(nlogn)	最好情况：O(logn) ， 最坏情况：O(n)	大型数据集，尤其是无序数据集
归并排序	O(nlogn)	O(n)	大型数据集，尤其是链表结构

如果对排序稳定性有要求，可以选择插入排序、归并排序。如果数据集较小且无序，可以选择冒泡排序、插入排序或选择排序。对于大型数据集，快速排序、归并排序通常效果更好。