超详细堆排序(动图演示)
文章目录
- 建堆的时间复杂度证明
- 俩种堆排序的思路
-
- 思路一:
-
- 第一步:创建堆,初始化堆
- 第二步: 将数据插入堆中,造成大堆
- 第三步:Pop k次
- 思路二:原地造堆
-
- 第一步:原地制造堆
- 第二步:对数组中内容进行处理
- 小结
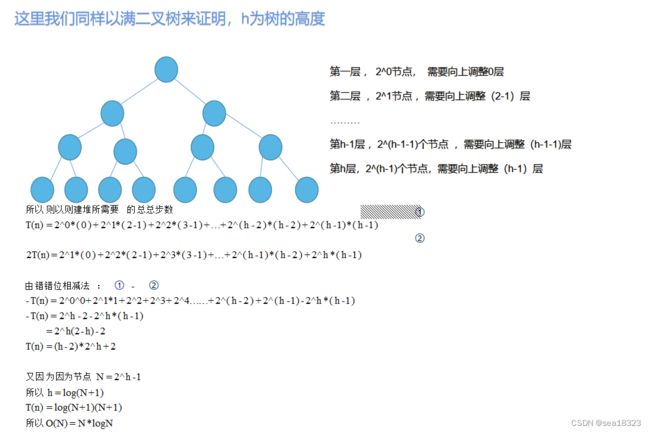
建堆的时间复杂度证明
向下调整法建堆的时间复杂度证明:
俩种堆排序的思路
下面的一些堆的接口在之前的堆实现中有所讲解:
链接:link
而我们本次的内容使用的主要是其中的向上调整和向下调整(堆排序俩大核心)
我们要对一个数组进行排序,利用堆有以下俩种方法:
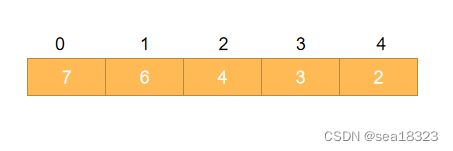
假设给定我们一个数组a[]={2,6,3,4,7};
本处以排降序举例
思路一:
1.创建堆,初始化堆
2.先将数组中的数插入堆中
3.pop N次
时间复杂度O(2N*logN) 空间复杂度为O(N)
在此我们先对对于第一种思路排升降序,建什么类型的堆做出说明
| 大小顺序 | 堆类型 |
|---|---|
| 升序 | 小堆 |
| 降序 | 大堆 |
解释:
根据我们之前讲的大堆,小堆的性质,下面我们先以排降序举例:我们知道大堆的堆顶的元素是元素中最大,而我们的堆排序的第一种思路主要运用Pop,就是先将堆顶的元素和堆尾元素互换,然后Pop掉堆顶元素,实际上是存储回原来的数组中,排升序也是类似思路。
第一步:创建堆,初始化堆
代码如下:
//1.建堆
Hp hp;
InitHeap(&hp);
(下面物理结构数组图没做好,多多包涵)
第二步: 将数据插入堆中,造成大堆
代码如下:
//将n个数插入堆中
for (int i = 0; i < n; i++)
{
PushHeap(&hp, a[i]);
}
第三步:Pop k次
Pop k实际上的操作是 每次将最大的数先移到堆顶,然后pop出去,再调整,再选出次大的数,以此类推,Pop到堆中没有数据时,就排好序了
代码实现如下:
for (int i = 0; i < n; i++)
{
a[i] = HeapTop(&hp);
PopHeap(&hp);
}
完整代码:
void Heapsort(int* a, int n) //n为数组大小
{
//1.建堆
Hp hp;
InitHeap(&hp);
//将n个数插入堆中
for (int i = 0; i < n; i++)
{
PushHeap(&hp, a[i]);
}
//然后pop n次
for (int i = 0; i < n; i++)
{
a[i] = HeapTop(&hp);
PopHeap(&hp);
}
}
思路二:原地造堆
上面思路一实现的是降序,这里我们来实现降序
1.先使用向上调整和向下调整进行原地构堆
2.再使用向下调整对数组内容进行处理
时间复杂度:向下调整法造堆:O(N+NlogN) 或 向上调整法构堆:O(2NlogN) 空间复杂度:O(1)
在此我们先对对于第二种思路排升降序,建什么类型的堆做出说明
| 大小顺序 | 堆类型 |
|---|---|
| 升序 | 大堆 |
| 降序 | 小堆 |
注意!!! 我们的第二种思路建的堆类型和第一种思路建的堆类型是反过来的,具体原因:见下面第二步的处理数组数据思路。
我们先对思路二的俩种在数组原地造堆的方式说明:
| 建堆方法 | 时间复杂度 | 思路 |
|---|---|---|
| 向上调整法 | O(N*logN) | 使用向上调整 从祖先的子树开始向上调整 即a[1] |
| 向下调整法 | O(N) | 使用向下调整 从第一个父亲节点开始向下调整 |
数组初始状态如下:
下面的图中序号为数组中的位置,并非下标注意哦!!!,下标应再减1

第一步:原地制造堆
解释:
就是从第一个父亲节点6(下标为1),进行向下调整,和较大的孩子7(下标4)进行交换,然后再到下一个父亲节点进行向下调整,就是祖先节点2(下标为0),先和左右孩子中较大的孩子7(新下标2)交换,然后再次将2与其左右孩子中较大的右孩子6(新下标4)交换
下图展示的是以向下调整法造堆:
//(2)方式二:使用向下调整 从第一个父亲节点开始向下调整 parent=(child-1)/2
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
Adjustdown(a, n, i);
}
第二步:对数组中内容进行处理
思路:
假设我们选择的是建大堆 排升序:
这个思路和我们Pop函数实现的时候有点相似,但不相同,相同点在于:每次都会将堆顶位置的元素和堆尾位置的元素进行交换,不同点:Pop函数实现时是将堆尾元素直接去掉,而我们是直接将堆的长度缩短1,然后再次对堆进行向下调整,将次大的元素选到堆顶,然后再次进行上面的操作,到堆被清空了就排好序了,建小堆排降序的思路也类似
建好堆之后的数组的形状是这样的: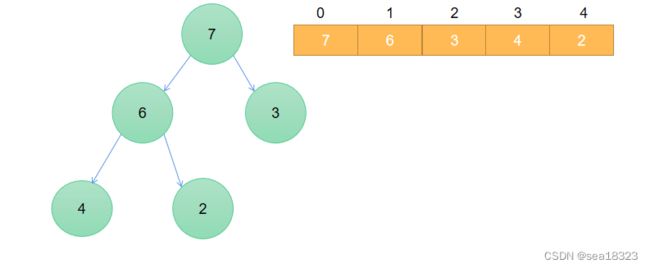
下面展示的是进行数据处理的图片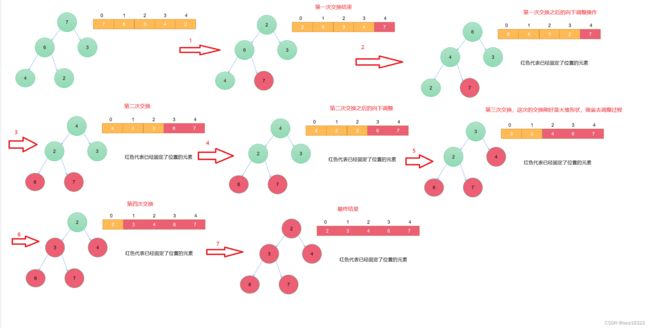
代码:
//2.开始选数
for (int end = n - 1; end>0; --end)
{
//选数
Swap(&a[0],&a[end]);
//调整 每次都把end位置处的数选出
Adjustdown(a, end, 0);
}
注:此处的Adjustdown要和之前的堆实现联系上
void Adjustdown(Datatype * tree,int n,int parent)
这里再解释一下每次将end位置处的数选出是怎么实现的,还是举例说明:
我们上面一开始进去,数组里面就是之前调整好的大堆了,end为4(即为数组最后一个位置的下标),然后我们再对堆进行向下调整,而我们可以看到我们传给函数的数据是这样的(a,4,0),而我们函数中的对应形参位置n代表的是数组个数,即我们这次向下调整的数组元素个数为4,然后这一次的循环走完了,执行 --end ,end就变为了3,即数组倒数第二个位置的下标,然后再次进行向下调整的数组元素个数就为3,依次类推,每个数都被选出来了。
思路二完整代码:
//方式二: 将传进来的数组原地构建成堆 1.构建成堆 2.向下调整选数(思路通topk) 时间复杂度:N+N*logN 空间复杂度O(1)
void Heapsort(int* a, int n)
{
//1.原地造堆
//(1)方式一:使用向上调整 从祖先的子树开始向上调整 即a[1]
/*for (int i = 1; i < n; i++)
{
AdjustUp(a, i);
}*/
//(2)方式二:使用向下调整 从第一个父亲节点开始向下调整 parent=(child-1)/2
for (int i = (n - 1 - 1) / 2; i >= 0; i--)
{
Adjustdown(a, n, i);
}
//2.开始选数
for (int end = n - 1; end>0; --end)
{
//选数
Swap(&a[0],&a[end]);
//调整 每次都把end位置处的数选出
Adjustdown(a, end, 0);
}
}
小结
| 造堆思路 | 造堆方法 | 时间复杂度 | 空间复杂度 |
|---|---|---|---|
| 利用数据结构堆 | 向上调整法 | O(2N*logN) | O(N) |
| 原地造堆1 | 向下调整法 | O(N+N*logN) | O(1) |
| 原地造堆2 | 向上调整法 | O(2*NlogN) | O(1) |
这里也解释一下上诉的时间复杂度是怎么计算出来的:
- 利用数据结构堆 :其中一个NlogN是利用向上调整法构堆所需的时间复杂度,另外一个是每次Pop的时候都需要使用向下调整,调整变成堆,因为时间复杂度考虑的是最坏情况,所以我们计算N个数据每次都需要向下调整高度层,然后又因为满二叉树的规律 N=2^h-1,所以高度h=log(N+1),所以调整N次的时间复杂度为Nlog(N)
- 原地造堆1:其中的N是我们使用向下调整法原地构堆的时间复杂度,上面我们证明过了,NlogN也是我们每次将堆顶和堆底的位置的元素互换后,要进行向下调整的时间复杂度,同样是考虑最坏情况,每次向下调整树的高度次,所以为NlogN,总体就是N+NlogN.
- 原地构堆2 :其中一个NlogN是我们使用向上调整构堆的时间复杂度,上面我们也已经证明过了,然后另一个NlogN也是我们每次将堆顶和堆底的位置的元素互换后,要进行向下调整的时间复杂度,同样是考虑最坏情况,每次向下调整树的高度次,所以为N*logN,总体就是2NlogN.
这里也最后做几点说明:
- 图中的N*NlogN前面的2是为了我们一开始更好的理解,实际算时间复杂度时,常数是去掉的
- 图中的N +N*logN,在计算时间复杂度时,是取俩者中的最大值作时间复杂度,这里也是方便理解
- 综合起来堆排序的时间复杂度其实是O(N*logN)
谢谢大佬们的观看,本文章到这就结束了,欢迎讨论学习。