统计的基本概念及抽样分布
文章目录
- 引言
- 总体(Population)
-
- 总体参数
- 样本(Sample)
-
- 随机样本
- 样本统计量
- 统计量(Statistic)
-
- 样本均值(Sample Mean)
- 样本方差和标准差(Sample Variance and Standard Deviation)
- 常用分布和分位点
-
- 1. 正态分布(Normal Distribution)
- 2. t分布(t-distribution)
- 3. χ²分布(Chi-Squared Distribution)
- 统计学中的应用
- 单个正态总体的抽样分布
- 两个正态总体的抽样分布
引言
统计学作为一门重要的科学领域,涵盖了众多的概念和方法。本文将重点介绍统计学的基本概念,包括总体、样本以及统计量,并将通过数学公式来解释它们之间的关系。
总体(Population)
总体是我们感兴趣的全体对象或观察单元的集合。在统计学中,总体可以包括人口、产品、事件等等。总体通常用大写字母N表示,总体的某一属性通常用大写字母X表示。例如,总体平均值用μ表示,总体标准差用σ表示。
总体参数
总体的属性可以通过各种参数来描述。例如,总体的均值、方差、标准差等都是描述总体性质的参数。这些参数通常是未知的,我们的目标是通过样本数据对它们进行估计。
样本(Sample)
由于通常不可能获取总体的全部数据,我们使用样本来代表总体。样本是总体中的一个子集,通常用小写字母n表示样本大小。样本的属性通常用小写字母x表示,例如样本均值用x̄表示。
随机样本
为了保证结果的代表性,样本需要是随机抽取的,这意味着每个总体成员被选中的概率应该是相等的。
样本统计量
样本统计量是从样本中计算出来的数值,用来估计总体参数。最常见的样本统计量包括样本均值、样本方差和样本标准差。这些统计量通常用帽子符号(^)表示,例如样本均值用x̄表示,样本标准差用s表示。
统计量(Statistic)
统计量是从样本数据计算出来的数值,用于对总体参数进行估计。统计量可以是点估计或区间估计。
样本均值(Sample Mean)
样本均值是样本中所有数据值的平均数,它通常用以下公式表示:
x̄ = (Σxi) / n
其中,x̄表示样本均值,Σxi表示所有样本数据的总和,n表示样本大小。
样本方差和标准差(Sample Variance and Standard Deviation)
样本方差是样本数据偏离均值的平方和的平均值,它通常用以下公式表示:
s² = Σ(xi - x̄)² / (n - 1)
样本标准差则是样本方差的平方根,它通常用以下公式表示:
s = √(Σ(xi - x̄)² / (n - 1))
其中,s²表示样本方差,s表示样本标准差,xi表示样本中的每个数据点,x̄表示样本均值,n表示样本大小。
常用分布和分位点
在统计学中,有一些常用的概率分布,它们用于描述不同类型的数据分布。这些分布在许多统计分析中都起着重要作用。本文将介绍一些常见的分布,包括正态分布、t分布和卡方分布,并讨论分位点的概念。
1. 正态分布(Normal Distribution)
正态分布也被称为高斯分布,它是最常见的概率分布之一。正态分布的概率密度函数(Probability Density Function,PDF)如下:

其中,xx 表示随机变量的取值,μμ 是均值,σσ 是标准差。正态分布是钟形曲线,均值位于分布的中心,标准差决定了曲线的宽度。
正态分布的分位点
正态分布的分位点是指分割概率分布的数值,通常以 zz 表示。正态分布的分位点可以用来计算概率或查找给定概率下的值。例如,第 αα 个百分位点(Percentile)表示在正态分布中,有 αα 的概率小于或等于该值。正态分布的分位点通常用 zαzα 表示,可以通过查找标准正态分布表格或计算得到。
2. t分布(t-distribution)
t分布是用于小样本中的统计推断的分布,它更广泛地适用于总体标准差未知的情况。t分布的PDF为:
f ( t ) = ( Γ ( ( ν + 1 ) / 2 ) / ( s q r t ( ν π ) ∗ Γ ( ν / 2 ) ) ) ∗ ( 1 + ( t 2 / ν ) ) ( − ( ν + 1 ) / 2 ) f(t) = (Γ((ν+1)/2) / (sqrt(νπ) * Γ(ν/2))) * (1 + (t²/ν))^(-(ν+1)/2) f(t)=(Γ((ν+1)/2)/(sqrt(νπ)∗Γ(ν/2)))∗(1+(t2/ν))(−(ν+1)/2)
其中,f(t)表示在t处的概率密度,ν表示自由度,Γ表示伽马函数。
分位点: t分布的分位点与自由度有关。例如,t分布的95%置信水平的上下分位点对应于自由度为n-1时,使得在这两个点之间的面积为0.95。
3. χ²分布(Chi-Squared Distribution)
χ²分布是用于分析卡方检验和构建置信区间的分布。它的PDF为:
f ( x ) = ( 1 / ( 2 ( k / 2 ) ∗ Γ ( k / 2 ) ) ) ∗ x ( k / 2 − 1 ) ∗ e ( − x / 2 ) f(x) = (1 / (2^(k/2) * Γ(k/2))) * x^(k/2 - 1) * e^(-x/2) f(x)=(1/(2(k/2)∗Γ(k/2)))∗x(k/2−1)∗e(−x/2)
其中,f(x)表示在x处的概率密度,k表示自由度,Γ表示伽马函数。
分位点: χ²分布的分位点同样与自由度有关。例如,χ²分布的95%置信水平的上下分位点对应于自由度为k时,使得在这两个点之间的面积为0.95。
统计学中的应用
这些常用分布和分位点在统计学中有广泛的应用。例如,正态分布用于描述许多自然现象,t分布用于小样本中的参数估计和假设检验,χ²分布用于分析离散型数据。分位点帮助我们计算概率、构建置信区间和进行假设检验,是统计学中不可或缺的工具。
总之,了解这些常用分布和分位点有助于我们更好地理解数据的分布特征,进行准确的统计分析,做出科学的决策。这些概念和数学工具为数据科学、经济学、医学研究等领域提供了坚实的基础。
单个正态总体的抽样分布
正态总体
首先,让我们简要介绍一下单个正态总体。正态总体(或称为正态分布总体)是一种连续概率分布,通常由其均值(μ)和标准差(σ)来描述。正态分布总体的概率密度函数(PDF)如下:
抽样分布是从一个总体中抽取多个样本,并计算每个样本的统计量(如样本均值)的分布。对于单个正态总体,如果我们从中抽取多个大小为 n 的随机样本,并计算每个样本的均值,那么这些样本均值的分布将近似于正态分布。这个近似性质可以通过中心极限定理来解释。
中心极限定理指出,当样本容量足够大时,这些样本均值的抽样分布将近似于正态分布,其均值等于总体均值 μ,标准差等于总体标准差 σ 除以 √n。这可以表示为:

这个结果对于统计推断非常重要,因为它允许我们使用正态分布的性质来进行置信区间估计和假设检验,即使我们不知道总体的分布形状。
两个正态总体的抽样分布
两个正态总体
现在,让我们考虑两个正态总体的情况。假设我们有两个独立的正态分布总体,分别具有均值 μ1 和 μ2,标准差 σ1 和 σ2。我们想要了解两个总体之间是否存在显著差异。
两个正态总体的抽样分布
当我们从两个正态总体中分别抽取两组样本,并计算这两组样本的差异(通常是均值之差)时,差异的抽样分布遵循一个特殊的分布,称为 t 分布。
具体来说,如果我们有两个独立的样本,每个样本大小为 n1 和 n2,且这两个样本分别来自两个正态总体,那么这两个样本均值之差的抽样分布近似于 t 分布。这个 t 分布的均值等于两个总体均值之差(μ1 - μ2),标准差由公式给出:
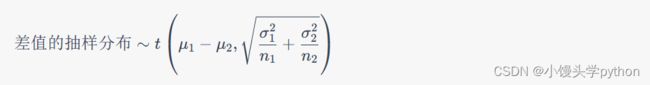
这个 t 分布在假设检验中经常用于比较两个总体均值是否有显著差异。通常,我们计算 t 统计量并与 t 分布的临界值进行比较,以确定是否拒绝假设。
总结起来,单个正态总体的抽样分布基于中心极限定理近似为正态分布,而两个正态总体的抽样分布涉及 t 分布,用于比较两个总体的均值差异。这些概念在统计学中是非常重要的,它们为数据分析和统计推断提供了强大的工具。
挑战与创造都是很痛苦的,但是很充实。
