【数据结构--二叉树】
文章目录
-
- 树的定义和基本性质
-
- 树的定义
- 树的特点
- 树的基本术语
- 二叉树
-
- 二叉树的定义
- 二叉树的特点
- 特殊二叉树
- 二叉树的性质
- 二叉树的代码实现
- 二叉树遍历
树的定义和基本性质
树的定义
树是一种非线性的数据结构,它是由n(n >= 0)个有限结点组成一个具有层次关系的集合T。如果n = 0,称为空树。如果n > 0,则T满足以下两个条件:①有且仅有一个根结点;②其他结点划分为m(m >= 0)个互不相交的有限集合T1 ,T2 ,…… ,Tm,其中每个集合又是一棵树,并且称之为根的子树。
树的特点
- 根结点可以有
0个或多个直接后继(其每棵子树的根结点),但没有直接前驱。 - 除根以外的其他结点有且仅有一个直接前驱,但可以有
0个或多个直接后继。 - 每一个非根结点有且仅有一个父结点。
- 除了根结点外,每个子结点可以分为多个不相交的子树。
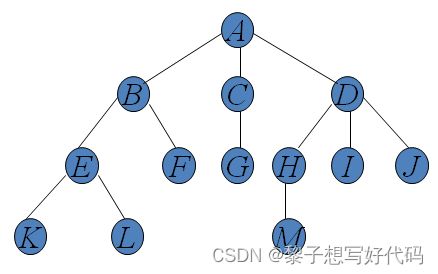
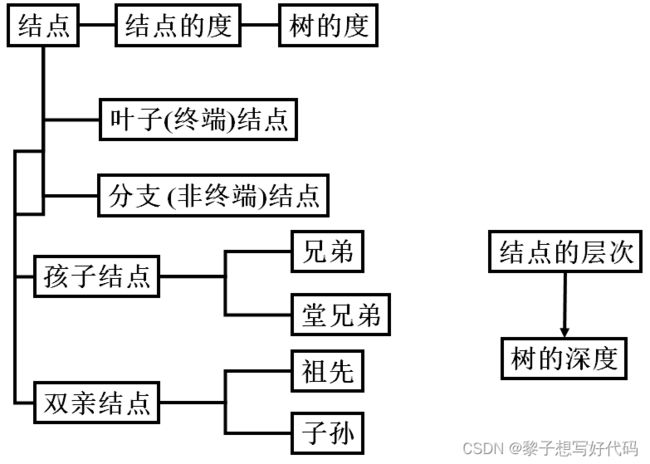
树的基本术语
结点的度:
结点拥有的子树数目称为结点的度
结点的关系:
结点子树的根结点为该结点的孩子结点。相应该结点称为孩子结点的双亲结点。
下图中,A为B的双亲结点,B为A的孩子结点。
同一个双亲结点的孩子结点之间互称兄弟结点。
下图中,结点B与结点C互为兄弟结点。
结点层次:
从根开始定义,根为第一层,根的孩子为第二层,以此类推,如下图。
森林:
互不相交的树的集合称为森林。森林和树间的联系:一棵树去掉根,其子树构成一片森林;一片森林增加一个根结点就成了一棵树。
二叉树
二叉树的定义
二叉树(Binary Tree)是n(n >= 0)个结点的有限集合,该集合或者为空集(称为空二叉树),或者由一个根结点和两棵互不相交的、分别称为根结点的左子树和右子树的二叉树组成。
二叉树的特点
- 每个结点最多有两棵子树,不存在度大于2的结点
- 左右子树有顺序,次序不可颠倒
- 即使树中某结点只有一棵子树,也要区别是左子树还是右子树
特殊二叉树
1. 斜树
所有结点都只有左子树的二叉树叫左斜树。所有结点都只有右子树的二叉树叫右斜树发,两者统称为斜树。
2. 满二叉树
在一棵二叉树中,如果所有分支结点都存在左子树和右子树,并且所有叶子都在同一层上,这样的二叉树称为满二叉树。
3. 完全二叉树
对一棵具有n个结点的二叉树按层序编号,如果编号为i(1 <= i <= n)的结点与同样深度的满二叉树中编号为i的结点在二叉树中位置完全相同,则这棵二叉树称为完全二叉树。
![]()
二叉树的性质
1. 在二叉树的第i层至多有2i-1个结点(i >= 1)。
2. 深度为k的二叉树至多有2k-1个结点(k >= 1)。
3. 对任何一棵二叉树T,如果其终端结点数为n0,度为2的结点数为n2,则n0 = n2 + 1。
4. 具有n个结点的完全二叉树的深度为 ⌊ l o g2 n ⌋ + 1 。
5. 如果对一棵 有n个结点的完全二叉树(其深度为⌊ l o g2 n ⌋ + 1)的结点按层序编号(从第1层到第⌊ l o g2 n ⌋ + 1层,每层从左到右),对任一结点i(1 <= i <= n)有:
( 1 )如果i = 1,则结点i是二叉树的根,无双亲;如果i > 1,则其双亲是结点 ⌊i / 2⌋。
( 2 )如果2i > n,则结点i无左孩子(结点i为叶子结点);否则其左孩子是结点2i。
( 3 )如果2i + 1 > n,则结点i无右孩子;否则其右孩子是结点2i + 1。
二叉树的代码实现
二叉树结构体定义
/* 二叉树结点 */
typedef char ElemType;
typedef struct BTNode
{
ElemType element;
BTNode* left;
BTNode* right;
} BTNode, *BTNodePtr;
/* 队列 */
typedef struct BTNodePtrQueue
{
BTNodePtr* nodePtrs;
int front;
int rear;
} BTNodePtrQueue, *QueuePtr;
初始化
/* 初始化队列 */
QueuePtr initQueue()
{
QueuePtr resultQueuePtr = (QueuePtr)malloc(sizeof(BTNodePtrQueue));
resultQueuePtr->nodePtrs = (BTNodePtr*)malloc(sizeof(BTNodePtr) * QUEUE_SIZE);
resultQueuePtr->front = 0;
resultQueuePtr->rear = 1;
return resultQueuePtr;
}
判断队列是否为空
/* 判断队列是否为空 */
bool isQueueEmpty(QueuePtr tempQueuePtr)
{
if((tempQueuePtr->front + 1) % QUEUE_SIZE == tempQueuePtr->rear)
{
return true;
}
return false;
}
结点入队
/* 结点入队 */
void Enqueue(QueuePtr tempQueuePtr, BTNodePtr tempBTNodePtr)
{
printf("front = %d, rear = %d.\n",tempQueuePtr->front,tempQueuePtr->rear);
if((tempQueuePtr->rear + 1) % QUEUE_SIZE == tempQueuePtr->front % QUEUE_SIZE)
{
printf("错误,%c入队失败:队列已满\n",tempBTNodePtr->element);
return ;
}
tempQueuePtr->nodePtrs[tempQueuePtr->rear] = tempBTNodePtr;
tempQueuePtr->rear = (tempQueuePtr->rear + 1) % QUEUE_SIZE;
printf("%c入队结束\n",tempBTNodePtr->element);
}
结点出队
/* 结点出队 */
BTNodePtr Dequeue(QueuePtr tempQueuePtr)
{
if(isQueueEmpty(tempQueuePtr))
{
printf("错误:队列为空\n");
return NULL;
}
tempQueuePtr->front = (tempQueuePtr->front + 1) % QUEUE_SIZE;
printf("%c出队结束\n",tempQueuePtr->nodePtrs[tempQueuePtr->front]->element);
return tempQueuePtr->nodePtrs[tempQueuePtr->front];
}
构造二叉树结点
/* 构造二叉树结点 */
BTNodePtr constructBTNode(ElemType tempElement)
{
BTNodePtr resultPtr = (BTNodePtr)malloc(sizeof(BTNode));
resultPtr->element = tempElement;
resultPtr->left = NULL;
resultPtr->right = NULL;
return resultPtr;
}
将字符串转换为二叉树
/* 将字符串转换为二叉树 */
BTNodePtr stringToBTree(char* tempString)
{
QueuePtr tempQueuePtr = initQueue();
BTNodePtr resultHeader;
BTNodePtr tempParent, tempLeftChild, tempRightChild;
int i = 0;
char ch = tempString[i];
resultHeader = constructBTNode(ch);
Enqueue(tempQueuePtr, resultHeader);
while (!isQueueEmpty(tempQueuePtr))
{
tempParent = Dequeue(tempQueuePtr);
++i;
ch = tempString[i];
if(ch == '#')
{
tempParent->left = NULL;
}else{
tempLeftChild = constructBTNode(ch);
Enqueue(tempQueuePtr, tempLeftChild);
tempParent->left = tempLeftChild;
}
++i;
ch = tempString[i];
if(ch == '#')
{
tempParent->right = NULL;
}else{
tempRightChild = constructBTNode(ch);
Enqueue(tempQueuePtr, tempRightChild);
tempParent->right = tempRightChild;
}
}
return resultHeader;
}
二叉树遍历
二叉树的遍历是指从根结点出发,按照某种次序依次访问二叉树中的所有结点,使得每个结点被访问一次且仅被访问一次。
1. 前序遍历
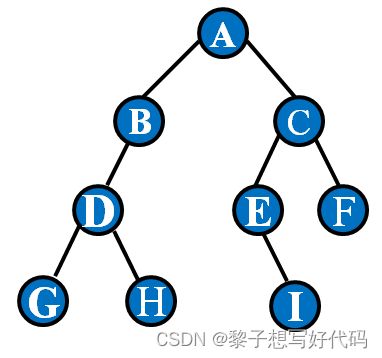
若二叉树为空,则空操作返回;否则先访问根结点,然后前序遍历左子树,再前序遍历右子树。如下图所示,遍历顺序为ABDGHCEIF。
前序遍历算法
/* 前序遍历 */
void preorder(BTNodePtr tempPtr)
{
if(tempPtr == NULL)
{
return ;
}
printf("%c",tempPtr->element);
preorder(tempPtr->left);
preorder(tempPtr->right);
}
2. 中序遍历
若二叉树为空,则空操作返回;否则从根结点开始(注意并不是先访问根结点),中序遍历根结点的左子树,然后是访问根结点,最后中序遍历右子树。如下图所示,遍历顺序为GDHBAEICF。
中序遍历算法
/* 中序遍历 */
void inorder(BTNodePtr tempPtr)
{
if(tempPtr == NULL)
{
return ;
}
inorder(tempPtr->left);
printf("%c",tempPtr->element);
inorder(tempPtr->right);
}
3. 后序遍历
若二叉树为空,则空操作返回;否则从左到右先叶子后结点的方式遍历访问左右子树,最后是访问根结点。如下图所示,遍历顺序为GHDBIEFCA。
后序遍历算法
/* 后序遍历 */
void postorder(BTNodePtr tempPtr)
{
if(tempPtr == NULL)
{
return ;
}
postorder(tempPtr->left);
postorder(tempPtr->right);
printf("%c",tempPtr->element);
}
4. 层序遍历
若二叉树为空,则空操作返回;否则从树的第一层,也就是根结点开始访问,从上而下逐层遍历,在同一层中,按从左到右的顺序对结点逐个访问。如下图所示,遍历顺序为ABCDEFGHI。
层序遍历算法
/* 层序遍历 */
void levelWise(BTNodePtr tempTreePtr)
{
char tempString[100];
int i = 0;
QueuePtr tempQueuePtr = initQueue();
BTNodePtr tempNodePtr;
Enqueue(tempQueuePtr, tempTreePtr);
while(!isQueueEmpty(tempQueuePtr))
{
tempNodePtr = Dequeue(tempQueuePtr);
tempString[i] = tempNodePtr->element;
++i;
if(tempNodePtr->left != NULL)
{
Enqueue(tempQueuePtr, tempNodePtr->left);
}
if(tempNodePtr->right != NULL)
{
Enqueue(tempQueuePtr, tempNodePtr->right);
}
}
tempString[i] = '\0';
printf("层序遍历:%s\n",tempString);
}
完整代码
#include 测试结果
只有一个结点.前序遍历:
c
front = 0, rear = 1.
a入队结束
a出队结束
front = 1, rear = 2.
c入队结束
front = 1, rear = 3.
d入队结束
c出队结束
front = 2, rear = 4.
e入队结束
d出队结束
front = 3, rear = 0.
b入队结束
front = 3, rear = 1.
f入队结束
e出队结束
b出队结束
f出队结束
前序遍历:acedbf
中序遍历:ecabdf
后序遍历:ecbfda
层序遍历:front = 0, rear = 1.
a入队结束
a出队结束
front = 1, rear = 2.
c入队结束
front = 1, rear = 3.
d入队结束
c出队结束
front = 2, rear = 4.
e入队结束
d出队结束
front = 3, rear = 0.
b入队结束
front = 3, rear = 1.
f入队结束
e出队结束
b出队结束
f出队结束
层序遍历:acdebf