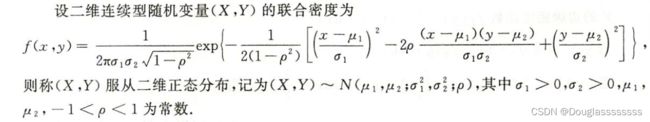【考研数学】概率论与数理统计 —— 第三章 | 二维随机变量及其分布（2，常见的二维随机变量及二维变量的条件分布和独立性）

---

引言

有了上文关于二维随机变量的基本概念与性质后，我们可以往后继续学习更加深入的内容。

---

四、常见的二维随机变量

4.1 二维均匀分布

设 $(X,Y)$ 为二维随机变量，$D$ 为 $xOy$ 平面的有限区域，其面积为 $A$ ，若 $(X,Y)$ 的联合密度函数为 $$f(x,y)=\{\begin{array}{ll}\frac{1}{A},& (x,y)\in D\\ 0,& (x,y)\notin D\end{array},$$ 称 $(X,Y)$ 为区域 $D$ 上的服从均匀分布。

可以回想一下一维的均匀分布，它是长度的倒数。

4.2 二维正态分布

这个我就不手敲了，太长啦，根本记不住。

其中，$\rho$ 为两个随机变量的相关系数。

若 $(X,Y)\sim N({\mu }_1,{\mu }_2;{\sigma }_1^2,{\sigma }_2^2;\rho )$ ，则 $X\sim N({\mu }_1,{\sigma }_1^2),Y\sim N({\mu }_2,{\sigma }_2^2).$ 当 $a^2+b^2\ne 0$ 时，有 $aX+bY$ 服从一维正态分布。随机变量 $X$ 和 $Y$ 独立的充要条件是两个变量不相关，即 $\rho \ne 0$ 。

---

五、二维随机变量的条件分布

5.1 二维离散型随机变量的条件分布律

设 $(X,Y)$ 为二维离散型随机变量，其联合分布律为 $$P\{X=x_i,Y=y_j\}=p_{ij}(i=1,2,\cdots ,m;j=1,2,\cdots ,n).$$ （1）对某个固定的 $i$ ，若 $P\{X=x_i\}>0$ ，则称 $$P\{Y=y_j|X=x_i\}=\frac{P\{X=x_i,Y=y_j\}}{P\{X=x_i\}}=\frac{p_{ij}}{p_{i\cdot }}(j=1,2,\cdots ,n)$$ 为在 $X=x_i$ 条件下随机变量 $Y$ 的条件分布律。

（2）对某个固定的 $j$ ，若 $P\{Y=y_j\}>0$ ，则称 $$P\{X=x_i|Y=y_j\}=\frac{P\{X=x_i,Y=y_j\}}{P\{Y=y_j\}}=\frac{p_{ij}}{p_{\cdot j}}(i=1,2,\cdots ,m)$$ 为在 $Y=y_i$ 条件下随机变量 $X$ 的条件分布律。

5.2 二维连续型随机变量的条件分布

设 $(X,Y)$ 为二维连续型随机变量，联合密度函数为 $f(x,y)$ ，变量 $X,Y$ 的边缘密度函数分别为 $f_X(x),f_Y(y).$

对固定的 $X=x$ ，若 $f_X(x)>0$ ，称 $$P\{Y\le y|X=x\}={\int }_{-\infty }^y\frac{f(x,y)}{f_X(x)}dy$$ 为在 $X=x$ 条件下 $Y$ 的条件分布函数，$\frac{f(x,y)}{f_X(x)}$ 为条件密度函数。对于固定的 $Y=y$ ，可同理得到类似结论。

我看老汤也没给证明，自己也没想明白为什么，就上网搜了下，发现是做了近似处理。

---

六、随机变量的独立性

6.1 基本概念

设 $A,B$ 为两个随机事件，若 $P(AB)=P(A)P(B)$ ，称事件 $A,B$ 独立；设 $(X,Y)$ 为二维随机变量，令 $\{X\le x\}=A,\{Y\le y\}=B$ ，则 $P(AB)=P(A)P(B)$ 等价于 $$F(x,y)=P\{X\le x,Y\le y\}=P\{X\le x\}P\{Y\le y\}=F_X(x)F_Y(y).$$ 于是有如下定义：

设 $(X,Y)$ 为二维随机变量，$F(x,y)$ 为其联合分布函数，$F_X(x),F_Y(y)$ 分别为 $X,Y$ 的边缘分布函数，若 $F(x,y)=F_X(x)=F_Y(y)$ ，称变量 $X,Y$ 相互独立。同理可扩展到 $n$ 维。

6.2 随机变量独立的等价条件

---

写在最后

其实如果一维的能掌握好一些，二维的可以类比来学，下一篇来说说二维随机变量的最后一个内容 —— 二维随机变量函数的分布。