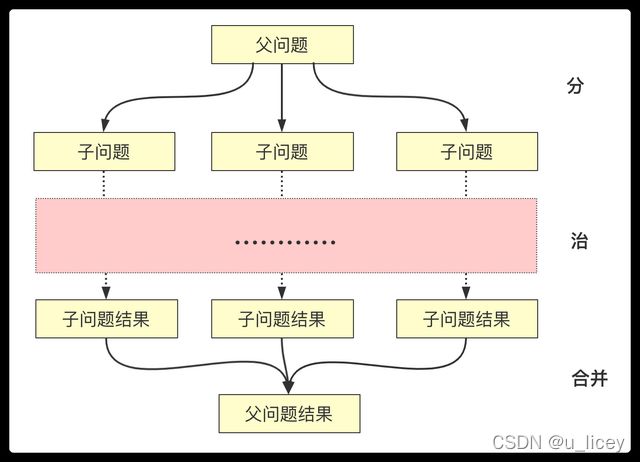
五大常用算法——分治法，动态规划，回溯法，分支界限法，贪心算法

(1) 分治法

将一个难以直接解决的大问题，分割成一些规模较小的相同问题

快速排序
快排也是分治的一个实例，快排每一趟会选定一个数，将比这个数小的放左面，比这个数大的放右面，
然后递归分治求解两个子区间，当然快排因为在分的时候就做了很多工作，
当全部分到最底层的时候这个序列的值就是排序完的值。这是一种分而治之的体现。

public void quicksort(int [] a,int left,int right){ 
  int low=left; 
  int high=right; //下面两句的顺序一定不能混，否则会产生数组越界！！！  very important！！！ 
  if(low>high)//作为判断是否截止条件 
  return; 
  int k=a[low];//额外空间k，取最左侧的一个作为衡量，最后要求左侧都比它小，右侧都比它大。 
  while(low<high)//这一轮要求把左侧小于a[low],右侧大于a[low]。 
  { 
  while(low<high&&a[high]>=k)//右侧找到第一个小于k的停止 
  { high--; } //这样就找到第一个比它小的了 
  a[low]=a[high];//放到low位置 
  while(low<high&&a[low]<=k)//在low往右找到第一个大于k的，放到右侧a[high]位置 
  { low++; } 
  a[high]=a[low];
  } 
  a[low]=k;//赋值然后左右递归分治求之 
  quicksort(a, left, low-1); 
  quicksort(a, low+1, right); 
}

归并排序(逆序数)
快排在分的时候做了很多工作，而归并就是相反，归并在分的时候按照数量均匀分，
而合并时候已经是两两有序的进行合并的，因为两个有序序列O(n)级别的复杂度即可得到需要的结果。
而逆序数在归并排序基础上变形同样也是分治思想求解。

private static void mergesort(int[] array, int left, int right) { 
  int mid=(left+right)/2; 
  if(left<right) { 
    mergesort(array, left, mid); 
    mergesort(array, mid+1, right); 
    merge(array, left,mid, right); 
    }
}
private static void merge(int[] array, int l, int mid, int r) { 
  int lindex=l;
  int rindex=mid+1; 
  int team[]=new int[r-l+1]; 
  int teamindex=0; 
  while (lindex<=mid&&rindex<=r) {//先左右比较合并 
    if(array[lindex]<=array[rindex]) { 
      team[teamindex++]=array[lindex++]; 
    } else { 
      team[teamindex++]=array[rindex++]; 
    } 
  } 
  while(lindex<=mid)//当一个越界后剩余按序列添加即可 
  { team[teamindex++]=array[lindex++]; } 
  while(rindex<=r) { team[teamindex++]=array[rindex++]; } 
  for(int i=0;i<teamindex;i++) { array[l+i]=team[i]; }
}

(2) 动态规划

动态规划算法与分治法类似，其基本思想也是将待求解问题分解成若干个子问题。

【初始状态】→【决策1】→【决策2】→…→【决策n】→【结束状态】

常见的应用场景有以下几个：

0-1背包问题（ ✔️）
矩阵连乘法（ ✔️）
硬币找零
字符串相似度
最长公共子序列
最长递增子序列
最大连续子序列和/积
有代价的最短路径
瓷砖覆盖（状态压缩DP）
工作量划分

    var value = [ 0, 1500, 3000, 2000]//分别对应物品a,b,c，为了方便人机交互，定义第0个物品为0
    var weight = [ 0, 1, 4, 3]//分别对应物品a,b,c，为了方便人机交互，定义第0个物品为0
    var bag = 4;//背包容量
    console.log('背包容量', re_OPT(3, 4))
    re_OPT(3, 4)

    /**
     * 动态规划：递归来求最优解
     * @param n 第n个物品
     * @param bag 背包容量
     * @return 最优解
     */
    function re_OPT(n, bag) {
      if (n == 0) {
        return 0;
      }
      if (bag >= weight[n]) {
        return Math.max(value[n] + re_OPT(n - 1, bag - weight[n]), re_OPT(n - 1, bag));
      } else {
        return re_OPT(n - 1, bag);
      }
    }

递归式实现了，仍然存在有个小问题。包含了大量的重复计算，极易引发栈溢出。

解法2，非递归实现动态规划算法
最终的答案，就在二维数组的右下角。

var value = [0, 1500, 3000, 2000]//分别对应物品a,b,c，为了方便人机交互，定义第0个物品为0
    var weight = [0, 1, 4, 3]//分别对应物品a,b,c，为了方便人机交互，定义第0个物品为0
    var bag = 4;//背包容量
    /**
 * 动态规划：非递归求最优解
 * @param n 第n个物品
 * @param bag 背包容量
 * @return 最优解
 */
    function dp_OPT(n, bag) {
      var result = []
      //将第一行与第一列重置为0
      for (var i = 0; i < weight.length; i++) {
        result[i] = [];
        for (var j = 1; j < bag + 1; j++) {
          result[i][j] = []
        }
      }
      //创造一个二维数组，用来存放各种情况对应的最优解,前[]保存第几个物品，后面[]保存多少背包容量
      for (var i = 0; i < result[0].length; i++) {
        result[0][i] = 0;
      }
      for (var j = 0; j < result.length; j++) {
        result[j][0] = 0;
      }
      for (var i = 1; i < result.length; i++) {
        for (var j = 1; j < result[0].length; j++) {
          result[i][j] = j >= weight[i] ? Math.max(value[i] + result[i - 1][j - weight[i]], result[i - 1][j]) : result[i - 1][j];
        }
      }
      return result[n][bag];
    }

(3) 回溯法

以深度优先的方式系统地搜索问题的解的方法称为回溯法。
可以系统地搜索一个问题的所有解或任意解。
有许多问题，当需要找出它的解集或者要求回答什么解是满足某些约束条件的最佳解时，往往要使用回溯法。
回溯法的基本做法是搜索，或是一种组织得井井有条的，能避免不必要搜索的穷举式搜索法。


https://blog.csdn.net/weixin_44705732/article/details/102650666

(4) 分支界限法

分支限界法常以广度优先或以最小耗费（最大效益）优先的方式搜索问题的解空间树。

(5) 贪心算法

把求解的问题分成若干个子问题
对每个子问题求解，得到子问题的局部最优解
把子问题的解局部最优解合成原来问题的一个解

该算法存在的问题
不能保证求得的最后解是最佳的
不能用来求最大值或最小值的问题
只能求满足某些约束条件的可行解的范围

实际上，贪心算法适用的情况很少。

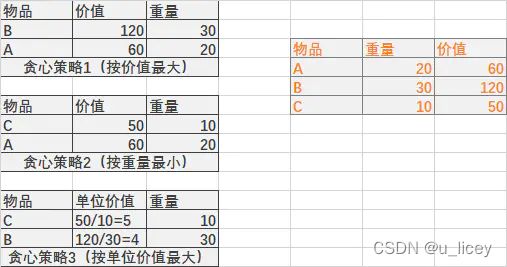
有三个物品A,B,C，其重量分别为{20,30,10}，价值分别为{60,120,50}，背包的容量为50，分别应用三种贪心策略装入背包的物品和获得的价值如下图所示：

分治法——>分成若干个子问题，例如“排序”。

动态规划——>分成若干个子问题，找出最优解。

贪心算法——>分成若干个子问题，局部最优解，不是最优解，不能用来求最大值或最小值的问题。

回溯法——>深度优先 遍历结点搜索解空间树。找出所有解。

分支限界法——>广度优先或最小耗费优先搜索解空间树。找出最优解。