Covid19:传染病模型SIR/SEIR的估计与拟合
Content
- Deterministic Model for Disease Spreading
-
- SIR model
- SEIR model
- Experiments for Deterministic Model based on Real Data
-
- SIR model fitting
- SEIR model fitting
github地址
Deterministic Model for Disease Spreading
Typical deterministic model for disease spreading includes SIR mode and SEIR model.
SIR model
The general SIR model takes s s s as the ratio of susceptible people, i i i as the infected people, r r r as the recovered people. Then we have:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ &\frac{ds}{dt}…
Here, β \beta β is the rate of transmission (transmissions per S-I contact per time), γ \gamma γ is the rate of recovery (inverse of infectious period). We could solve these equation and get:
s = s 0 e − β γ r s=s_0e^{-\frac{\beta}{\gamma}r} s=s0e−γβr
With s + i + r = 1 s+i+r=1 s+i+r=1, we could drive:
d r d t = γ ( 1 − r − s 0 e − β γ r ) t = 1 γ ∫ 0 r d u 1 − u − s 0 e − β γ u \frac{dr}{dt}=\gamma (1-r-s_0e^{-\frac{\beta}{\gamma}r})\\ t=\frac{1}{\gamma}\int_0^r\frac{du}{1-u-s_0e^{-\frac{\beta}{\gamma}u}} dtdr=γ(1−r−s0e−γβr)t=γ1∫0r1−u−s0e−γβudu
With the above equations, we could fit the lines of the rate of susceptible, infectious and recovered people and get the parameter estimation of γ \gamma γ and β \beta β.
Also, we could drive their iteration form with S = s N , I = i N , R = r N S=sN, I=iN, R=rN S=sN,I=iN,R=rN and let c c c be the number of people one contact:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ & S_n=S_{n-1}-…
SEIR model
The general SEIR model takes s s s as the ratio of susceptible people, e e e as the exposed people, i i i as the infected people, r r r as the recovered people. Then we have:
KaTeX parse error: No such environment: align at position 8: \begin{̲a̲l̲i̲g̲n̲}̲ &\frac{ds}{dt}…
Here, β \beta β is the rate of transmission (transmissions per S-I contact per time), γ \gamma γ is the rate of recovery (inverse of infectious period), α \alpha α is the rate of progression (inverse of incubation period). We could solve these equation and get:
s = s 0 e − β γ r s=s_0e^{-\frac{\beta}{\gamma}r} s=s0e−γβr
With s + e + i + r = 1 s+e+i+r=1 s+e+i+r=1, we could drive:
d r d t = γ ( 1 − e − r − s 0 e − β γ r ) t = 1 γ ∫ 0 r d u 1 − e − u − s 0 e − β γ u \frac{dr}{dt}=\gamma (1-e-r-s_0e^{-\frac{\beta}{\gamma}r})\\ t=\frac{1}{\gamma}\int_0^r\frac{du}{1-e-u-s_0e^{-\frac{\beta}{\gamma}u}} dtdr=γ(1−e−r−s0e−γβr)t=γ1∫0r1−e−u−s0e−γβudu
With the above equations, we could fit the lines of the rate of susceptible, infectious and recovered people and get the parameter estimation of γ \gamma γ and β \beta β.
Also, we could drive their iteration form with S = s N , E = e N , I = i N , R = r N S=sN, E=eN,I=iN, R=rN S=sN,E=eN,I=iN,R=rN and let c c c be the number of people one contact:
S n = S n − 1 − c β I n − 1 S n − 1 N E n = E n − 1 + c β I n − 1 S n − 1 N − α E n − 1 I n = I n − 1 + α E n − 1 − γ I n − 1 R n = R n − 1 + γ I n − 1 S_n=S_{n-1}-\frac{c\beta I_{n-1}S_{n-1}}{N}\\ E_n=E_{n-1}+c\beta I_{n-1}S_{n-1}N-\alpha E_{n-1}\\ I_n=I_{n-1}+\alpha E_{n-1}-\gamma I_{n-1}\\ R_n=R_{n-1}+\gamma I_{n-1}\\ Sn=Sn−1−NcβIn−1Sn−1En=En−1+cβIn−1Sn−1N−αEn−1In=In−1+αEn−1−γIn−1Rn=Rn−1+γIn−1
Experiments for Deterministic Model based on Real Data
SIR model fitting
Here, we use the data from Jaunary 2end 2020 to May 9th 2020 of Shenzhen, including the cummulative confirmed cases, cummulative cured cases and cummulative dead cases. Here, we apply SIR model and fit the data of Shenzhen to get the s s s the ratio of susceptible people, i i i as the infected people, r r r as the recovered people.
data=pd.read_excel("02_SZ_DailyCases.xlsx")
data.head()
| City | Date | cummulative confirmed cases | cummulative cured cases | cummulative dead cases | |
|---|---|---|---|---|---|
| 0 | Shenzhen | 2020-01-20 | 9 | 0 | 0 |
| 1 | Shenzhen | 2020-01-21 | 14 | 0 | 0 |
| 2 | Shenzhen | 2020-01-22 | 15 | 0 | 0 |
| 3 | Shenzhen | 2020-01-23 | 15 | 2 | 0 |
| 4 | Shenzhen | 2020-01-24 | 20 | 2 | 0 |
m i n i m i z e α 1 ( ∑ i = 1 n ( s i ^ − s i ) 2 + ( 1 − α 1 ) ( ∑ i = 1 n ( r i ^ − r i ) S e t α 1 = 0.1 minimize ~~\alpha_1 (\sum_{i=1}^n (\hat{s_i}-s_i)^2+(1-\alpha_1)(\sum_{i=1}^n (\hat{r_i}-r_i)\\ Set ~ \alpha_1=0.1 minimize α1(i=1∑n(si^−si)2+(1−α1)(i=1∑n(ri^−ri)Set α1=0.1
#!/usr/bin/python
import numpy as np
import pandas as pd
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
import matplotlib.pyplot as plt
from datetime import timedelta, datetime
predict_range = 150
s_0=99998
i_0=2
r_0=0
class Learner(object):
def __init__(self, loss, predict_range, s_0, i_0, r_0):
self.loss = loss
self.predict_range = predict_range
self.s_0 = s_0
self.i_0 = i_0
self.r_0 = r_0
def load_confirmed(self):
df = pd.read_csv('./model_fit/02_SZ_DailyCases.csv')
df.set_index(["Date"], inplace=True)
dff=df["cummulative confirmed cases"]
return dff.T
def load_recovered(self):
df = pd.read_csv('./model_fit/02_SZ_DailyCases.csv')
df.set_index(["Date"], inplace=True)
dff = df["cummulative cured cases"]
return dff.T
def load_dead(self):
df = pd.read_csv('./model_fit/02_SZ_DailyCases.csv')
df.set_index(["Date"], inplace=True)
dff = df["cummulative dead cases"]
return dff.T
def extend_index(self, index, new_size):
values = index.values
current = datetime.strptime(index[-1], '%m/%d/%y')
while len(values) < new_size:
current = current + timedelta(days=1)
values = np.append(values, datetime.strftime(current, '%m/%d/%y'))
return values
def predict(self, beta, gamma, data, recovered, death, s_0, i_0, r_0):
new_index = self.extend_index(data.index, self.predict_range)
size = len(new_index)
def SIR(t, y):
S = y[0]
I = y[1]
R = y[2]
return [-beta * S * I, beta * S * I - gamma * I, gamma * I]
extended_actual = np.concatenate((data.values, [None] * (size - len(data.values))))
extended_recovered = np.concatenate((recovered.values, [None] * (size - len(recovered.values))))
extended_death = np.concatenate((death.values, [None] * (size - len(death.values))))
return new_index, extended_actual, extended_recovered, extended_death, solve_ivp(SIR, [0, size],
[s_0, i_0, r_0],
t_eval=np.arange(0, size, 1))
def train(self):
recovered = self.load_recovered()
death = self.load_dead()
data = (self.load_confirmed() - recovered - death)
optimal = minimize(loss, [0.001, 0.001], args=(data, recovered, self.s_0, self.i_0, self.r_0),
method='L-BFGS-B', bounds=[(0.00000001, 0.4), (0.00000001, 0.4)])
print(optimal)
beta, gamma = optimal.x
new_index, extended_actual, extended_recovered, extended_death, prediction = self.predict(beta, gamma, data,
recovered, death,
self.s_0, self.i_0,
self.r_0)
df = pd.DataFrame(
{'Infected data': extended_actual, 'Recovered data': extended_recovered, 'Death data': extended_death,
'Susceptible': prediction.y[0], 'Infected': prediction.y[1], 'Recovered': prediction.y[2]},
index=new_index)
fig, ax = plt.subplots(figsize=(15, 10))
#ax.set_title(self.country)
df.plot(ax=ax)
print(f" beta={beta:.8f}, gamma={gamma:.8f}, r_0:{(beta / gamma):.8f}")
fig.savefig("result.png")
def loss(point, data, recovered, s_0, i_0, r_0):
size = len(data)
beta, gamma = point
def SIR(t, y):
S = y[0]
I = y[1]
R = y[2]
return [-beta * S * I, beta * S * I - gamma * I, gamma * I]
solution = solve_ivp(SIR, [0, size], [s_0, i_0, r_0], t_eval=np.arange(0, size, 1), vectorized=True)
l1 = np.sqrt(np.mean((solution.y[1] - data) ** 2))
l2 = np.sqrt(np.mean((solution.y[2] - recovered) ** 2))
alpha = 0.1
return alpha * l1 + (1 - alpha) * l2
def main():
learner = Learner(loss, predict_range, s_0, i_0, r_0)
learner.train()
if __name__ == '__main__':
main()
fun: 192.0426614226907
hess_inv: <2x2 LbfgsInvHessProduct with dtype=float64>
jac: array([208799.102424 , -539.91772688])
message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
nfev: 87
nit: 5
status: 0
success: True
x: array([9.12866787e-07, 2.39518331e-07])
beta=0.00000091, gamma=0.00000024, r_0:3.81126064
The results are beta=0.00000091, gamma=0.00000024, r_0:3.81126064
Also, we draw the graph with 150 days of prediction.
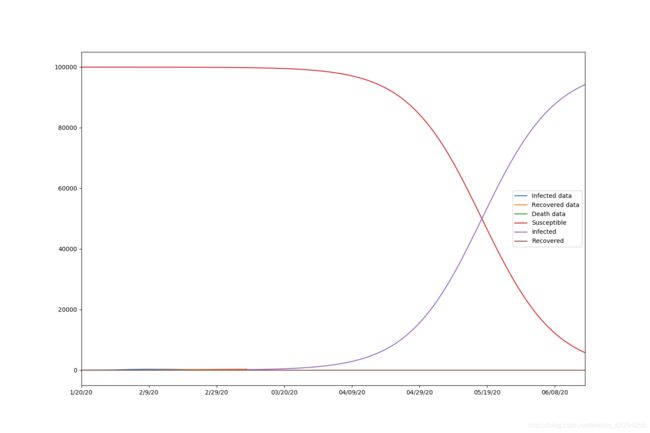
SEIR model fitting
For SEIR model, since we could not get the data of exposed people, we simpy assume that the exposed people is a static ratio of the confirmed cases. Here, we set it as 0.1 to get the model fit parameters.
m i n i m i z e α 1 ( ∑ i = 1 n ( s i ^ − s i ) 2 + α 2 ( ∑ i = 1 n ( e i ^ − e i ) + ( 1 − α 1 − α 2 ) ( ∑ i = 1 n ( r i ^ − r i ) S e t α 1 = 0.1 , α 2 = 0.1 minimize~~~~ \alpha_1 (\sum_{i=1}^n (\hat{s_i}-s_i)^2+\alpha_2(\sum_{i=1}^n (\hat{e_i}-e_i)+(1-\alpha_1-\alpha_2)(\sum_{i=1}^n (\hat{r_i}-r_i)\\ Set ~ \alpha_1=0.1,\alpha_2=0.1 minimize α1(i=1∑n(si^−si)2+α2(i=1∑n(ei^−ei)+(1−α1−α2)(i=1∑n(ri^−ri)Set α1=0.1,α2=0.1
#!/usr/bin/python
import numpy as np
import pandas as pd
from scipy.integrate import solve_ivp
from scipy.optimize import minimize
import matplotlib.pyplot as plt
from datetime import timedelta, datetime
predict_range = 150
s_0=99990
e_0=8
i_0=2
r_0=0
ratio=0.5
class Learner(object):
def __init__(self, loss, predict_range, s_0, e_0,i_0, r_0):
self.loss = loss
self.predict_range = predict_range
self.s_0 = s_0
self.e_0 = e_0
self.i_0 = i_0
self.r_0 = r_0
def load_confirmed(self):
df = pd.read_csv('./model_fit/02_SZ_DailyCases.csv')
df.set_index(["Date"], inplace=True)
dff=df["cummulative confirmed cases"]
return dff.T
def load_exposed(self,ratio):
df = pd.read_csv('./model_fit/02_SZ_DailyCases.csv')
df.set_index(["Date"], inplace=True)
dff=df["cummulative confirmed cases"]
dfff=dff*ratio
return dfff.T
def load_recovered(self):
df = pd.read_csv('./model_fit/02_SZ_DailyCases.csv')
df.set_index(["Date"], inplace=True)
dff = df["cummulative cured cases"]
return dff.T
def load_dead(self):
df = pd.read_csv('./model_fit/02_SZ_DailyCases.csv')
df.set_index(["Date"], inplace=True)
dff = df["cummulative dead cases"]
return dff.T
def extend_index(self, index, new_size):
values = index.values
current = datetime.strptime(index[-1], '%m/%d/%y')
while len(values) < new_size:
current = current + timedelta(days=1)
values = np.append(values, datetime.strftime(current, '%m/%d/%y'))
return values
def predict(self, beta, alpha, gamma, data, exposed, recovered, death, s_0, e_0, i_0, r_0):
new_index = self.extend_index(data.index, self.predict_range)
size = len(new_index)
def SEIR(t, y):
S = y[0]
E = y[1]
I = y[2]
R = y[3]
return [-beta * S * I, beta * S * I - alpha* E, alpha* E- gamma * I, gamma * I]
extended_actual = np.concatenate((data.values, [None] * (size - len(data.values))))
extended_exposed = np.concatenate((exposed.values, [None] * (size - len(exposed.values))))
extended_recovered = np.concatenate((recovered.values, [None] * (size - len(recovered.values))))
extended_death = np.concatenate((death.values, [None] * (size - len(death.values))))
return new_index, extended_actual, extended_exposed, extended_recovered, extended_death, solve_ivp(SEIR,[0, size],
[s_0, e_0,i_0, r_0],
t_eval=np.arange(0, size, 1))
def train(self):
recovered = self.load_recovered()
exposed = self.load_exposed(ratio)
death = self.load_dead()
data = (self.load_confirmed() - exposed - recovered - death)#易感人数
optimal = minimize(loss, [0.001, 0.001, 0.001], args=(data, exposed, recovered, self.s_0, self.e_0, self.i_0, self.r_0),
method='L-BFGS-B', bounds=[(0.00000001, 0.4), (0.00000001, 0.4), (0.00000001, 0.4)])
print(optimal)
beta, alpha, gamma = optimal.x
new_index, extended_actual, extended_exposed, extended_recovered, extended_death, prediction = self.predict(beta, alpha, gamma, data, exposed, recovered, death,
self.s_0, self.e_0,self.i_0,
self.r_0)
df = pd.DataFrame(
{'Infected data': extended_actual, 'Recovered data': extended_recovered, 'Death data': extended_death,
'Susceptible': prediction.y[0], 'Exposed': prediction.y[1], 'Infected': prediction.y[2], 'Recovered': prediction.y[3]},
index=new_index)
fig, ax = plt.subplots(figsize=(15, 10))
#ax.set_title(self.country)
df.plot(ax=ax)
print(f" beta={beta:.8f}, alpha={alpha:.8f}, gamma={gamma:.8f}, r_0:{(beta / gamma):.8f}")
fig.savefig("result_SEIR.png")
fig.show()
print(df)
def loss(point, data, exposed, recovered, s_0, e_0, i_0, r_0):
size = len(data)
beta, alpha, gamma = point
def SEIR(t, y):
S = y[0]
E = y[1]
I = y[2]
R = y[3]
return [-beta * S * I, beta * S * I - alpha * E, alpha * E - gamma * I, gamma * I]
solution = solve_ivp(SEIR, [0, size], [s_0, e_0, i_0, r_0], t_eval=np.arange(0, size, 1), vectorized=True)
l1 = np.sqrt(np.mean((solution.y[1] - data) ** 2))
l2 = np.sqrt(np.mean((solution.y[2] - exposed) ** 2))
l3 = np.sqrt(np.mean((solution.y[3] - recovered) ** 2))
a1 = 0.1
a2 = 0.1
return a1 * l1 + a2 * l2 + (1 - a1 - a2) * l3
def main():
learner = Learner(loss, predict_range, s_0, e_0, i_0, r_0)
learner.train()
if __name__ == '__main__':
main()
fun: 111.62004441579865
hess_inv: <3x3 LbfgsInvHessProduct with dtype=float64>
jac: array([ 5.88108459e+06, 2.35953219e+02, -1.84868701e+02])
message: b'CONVERGENCE: REL_REDUCTION_OF_F_<=_FACTR*EPSMCH'
nfev: 180
nit: 16
status: 0
success: True
x: array([1.42325627e-05, 5.08089942e-02, 4.00000000e-01])
beta=0.00001423, alpha=0.05080899, gamma=0.40000000, r_0:0.00003558
Infected data Recovered data Death data Susceptible Exposed \
1/20/20 4.5 0 0 99990.000000 8.000000
1/21/20 7 0 0 99987.374417 10.162146
1/22/20 7.5 0 0 99985.007648 11.965733
1/23/20 5.5 2 0 99982.704533 13.618636
1/24/20 8 2 0 99980.347766 15.242162
... ... ... ... ... ...
06/13/20 None None None 5046.380713 9661.000189
06/14/20 None None None 4951.104209 9275.303313
06/15/20 None None None 4861.351492 8903.325929
06/16/20 None None None 4776.860612 8544.620430
06/17/20 None None None 4697.113617 8199.057671
Infected Recovered
1/20/20 2.000000 0.000000
1/21/20 1.725445 0.737992
1/22/20 1.623365 1.403254
1/23/20 1.626192 2.050639
1/24/20 1.696952 2.713121
... ... ...
06/13/20 1363.575498 83929.043601
06/14/20 1308.856933 84464.735545
06/15/20 1256.480752 84978.841826
06/16/20 1206.930025 85471.588933
06/17/20 1159.089167 85944.739545
[150 rows x 7 columns]
The results are beta=0.00001423, alpha=0.05080899, gamma=0.40000000, r_0:0.00003558.
Also, we draw the graph with 150 days of prediction.
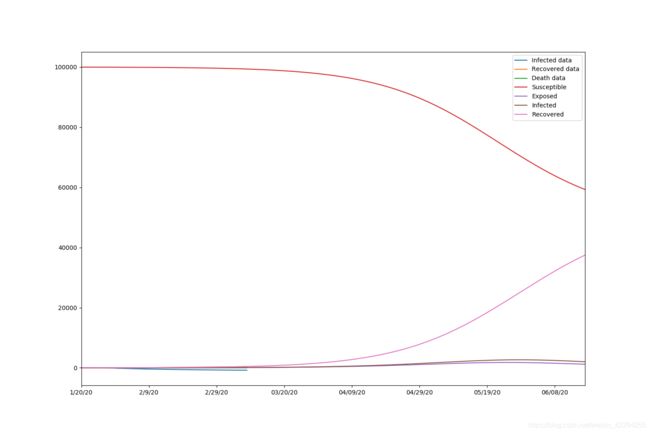
.
欢迎关注二幺子的知识输出通道: