算法篇之(排序)
前言:算法中排序也是经常用到的,今天学习排序的几大经典算法(python语言实现)。
目录
冒泡排序
代码解读
时间复杂度分析
选择排序
代码解读
时间复杂度分析
插入排序
代码解读
时间复杂度分析
希尔排序
代码解读
时间复杂度分析
归并排序
代码解读
时间复杂度分析
快速排序
代码解读
时间复杂度分析
桶排序
代码解读
时间复杂度分析
计数排序
代码解读
时间复杂度分析
基数排序
代码解读
时间复杂度分析
堆排序
代码解读
时间复杂度分析
总结
冒泡排序
1.1 冒泡排序 | 菜鸟教程 (runoob.com)
代码:
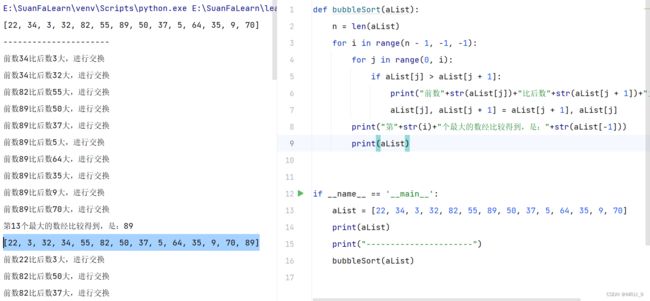
def bubble_sort(alist):
n = len(alist)
for i in range(n - 1, -1, -1):
for j in range(0, i):
if alist[j] > alist[j + 1]:
alist[j], alist[j + 1] = alist[j + 1], alist[j]代码解读
case:[22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70]
- len函数获取列表的长度,例子中数组长度为14,下标范围为:0-13
- 第一层for循环,倒着取出下标,13-0
- 第二层for循环,取出range(0,i)范围内的数,i是第一层循环取出的下标,即第二层循环,分别取出range(0,13)、range(0,12)……range(0,1),range(0,0)
- 依次比较取出的数作为下标,在列表里对应的值,如果前一个数比后面的数大,则将两个数互换,alist[ j ], alist[ j + 1 ] = alist[ j + 1 ], alist[ j ],这行代码是python语言特有的写法,表示将两个数进行交换
时间复杂度分析
O(N^2)
有两层for循环, 看一下最差的情况
外层for循环,执行次数为N
内层for循环,第一次比较了n-1,第二次比较了n-2,……,第N-1次比较了1次,加起来,总的执行次数复杂度为N
复杂度为N*2
选择排序
1.2 选择排序 | 菜鸟教程 (runoob.com)
def select_sort(alist):
n = len(alist)
for j in range(n - 1):
min_index = j
for i in range(j + 1, n):
if alist[min_index] > alist[i]:
min_index = i
alist[j], alist[min_index] = alist[min_index], alist[j]代码解读
case:[22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70]
- len函数获取列表的长度,例子中数组长度为14,下标范围为:0-13
- 第一层for循环,取出列表的每一个下标
- 第二层for循环,从每个下标,往后一直找到结束
- 分为两个部分:所在的第一个下标和未排好序的部分,未排好序的部分的所有数,与第一个下标所在的值,依次进行对比,如果找到最小的数,则将两者进行交换
时间复杂度分析
时间复杂度:N^2
循环了两次,外层循环和内层循环,时间复杂度为N^2
插入排序
1.3 插入排序 | 菜鸟教程 (runoob.com)
def InsertionSort(aList):
n = len(aList)
for i in range(1, n):
x = aList[i]
j = i - 1
while j >= 0:
if x <= aList[j]:
aList[j + 1] = aList[j]
j -= 1
else:
break
aList[j + 1] = x代码解读
case:[22, 34, 3, 32, 82, 55, 89, 50, 37, 5, 64, 35, 9, 70]
- len函数获取列表的长度,例子中数组长度为14,下标范围为:0-13
- 第一层for循环,取出列表的每一个下标(不包括下标为0的),取出每个下标对应的数
- 将第一待排序序列第一个元素看做一个有序序列,把第二个元素到最后一个元素当成是未排序序列。从头到尾依次扫描未排序序列,将扫描到的每个元素插入有序序列的适当位置。
时间复杂度分析
N^2
需要循环两次,时间复杂度为N^2
希尔排序
1.4 希尔排序 | 菜鸟教程 (runoob.com)
def ShellSort(aList):
n = len(aList)
gap = n // 2
while gap > 0:
for i in range(gap, n):
x = aList[i]
j = i
while j >= gap:
if x < aList[j - gap]:
aList[j] = aList[j - gap]
else:
break
j -= gap
aList[j] = x
print(aList)
gap = gap // 2代码解读
- 选择一个增量序列
- 按增量序列个数 k,对序列进行 k 趟排序;
- 每趟排序,根据对应的增量 ti,将待排序列分割成若干长度为 m 的子序列,分别对各子表进行直接插入排序。仅增量因子为 1 时,整个序列作为一个表来处理,表长度即为整个序列的长度。
时间复杂度分析
希尔排序时间复杂度有点复杂,排序的效率是取决于它的增量序列。时间复杂度在O(nlogn~n^2)之间
归并排序
1.5 归并排序 | 菜鸟教程 (runoob.com)
def Merge(aList, start, mid, end):
tmp = []
L = start
r = mid + 1
while L <= mid and r <= end:
if aList[L] <= aList[r]:
tmp.append(aList[L])
L += 1
else:
tmp.append(aList[r])
r += 1
tmp.extend(aList[L:mid + 1])
tmp.extend(aList[r:end + 1])
for i in range(start, end + 1):
aList[i] = tmp[i - start]
print(start, end, tmp)
def MergeSort(aList, start, end):
if start == end:
return
mid = (start + end) // 2
MergeSort(aList, start, mid)
MergeSort(aList, mid + 1, end)
Merge(aList, start, mid, end)代码解读
- 申请空间,大小为为两个已经排序序列之和,该空间用来存放合并后的序列
- 设定两个指针,最初位置分别为两个已经排序序列的起始位置
- 比较两个指针所指向的元素,选择相对小的元素放入到合并空间,并移动指针到下一位置
- 重复步骤 3 直到某一指针达到序列尾
- 将另一序列剩下的所有元素直接复制到合并序列尾
时间复杂度分析
O(NlogN)
归并排序用到了递归和分治的思想,列表长度为N,用二分法分解,为logN,合在一起,复杂度是O(NlogN)
快速排序
1.6 快速排序 | 菜鸟教程 (runoob.com)
def QucikSortPivot(aList, start, end):
pivot = start
j = start + 1
for i in range(start + 1, end + 1):
if aList[i] <= aList[pivot]:
aList[i], aList[j] = aList[j], aList[i]
j += 1
aList[pivot], aList[j - 1] = aList[j - 1], aList[pivot]
pivot = j - 1
print(aList[pivot], aList[start:pivot], aList[pivot + 1:end + 1])
return pivot
def QuickSort(aList, start, end):
if start >= end:
return
pivot = QucikSortPivot(aList, start, end)
QuickSort(aList, start, pivot - 1)
QuickSort(aList, pivot + 1, end)随机快速排序
import random
def QucikSortPivot(aList, start, end):
randIndex = random.randint(start,end)
aList[start],aList[randIndex] = aList[randIndex],aList[start]
pivot = start
j = start + 1
for i in range(start + 1, end + 1):
if aList[i] <= aList[pivot]:
aList[i], aList[j] = aList[j], aList[i]
j += 1
aList[pivot], aList[j - 1] = aList[j - 1], aList[pivot]
pivot = j - 1
print(aList[pivot], aList[start:pivot], aList[pivot + 1:end + 1])
return pivot
def QuickSort(aList, start, end):
if start >= end:
return
pivot = QucikSortPivot(aList, start, end)
QuickSort(aList, start, pivot - 1)
QuickSort(aList, pivot + 1, end)代码解读
- 从数列中挑出一个元素,称为 "基准"(pivot)(可以随机,随机快速排序就是随机取的)
- 重新排序数列,所有元素比基准值小的摆放在基准前面,所有元素比基准值大的摆在基准的后面(相同的数可以到任一边)。在这个分区退出之后,该基准就处于数列的中间位置。这个称为分区(partition)操作
- 递归地(recursive)把小于基准值元素的子数列和大于基准值元素的子数列排序
时间复杂度分析
最坏时间复杂度:O(N^2)
桶排序
1.9 桶排序 | 菜鸟教程 (runoob.com)
def SelectSort(aList):
n = len(aList)
for i in range(0, n):
min = i
for j in range(i + 1, n):
if aList[j] < aList[min]:
min = j
aList[i], aList[min] = aList[min], aList[i]
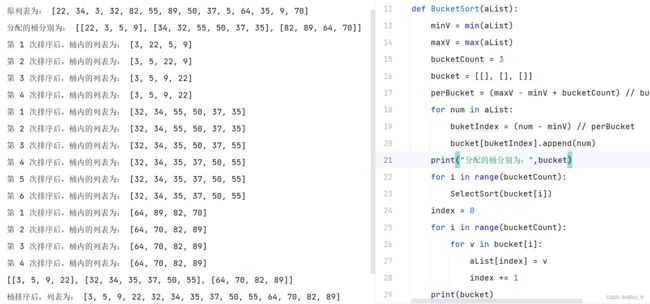
def BucketSort(aList):
minV = min(aList)
maxV = max(aList)
bucketCount = 3
bucket = [[], [], []]
perBucket = (maxV - minV + bucketCount) // bucketCount
for num in aList:
buketIndex = (num - minV) // perBucket
bucket[buketIndex].append(num)
for i in range(bucketCount):
SelectSort(bucket[i])
index = 0
for i in range(bucketCount):
for v in bucket[i]:
aList[index] = v
index += 1代码解读
- 桶排序的核心思路是:先给数分配桶,元素在每个桶内排序,再按桶的顺序,进行所有数据的排序
- 先看一下分配桶的思路:找到数组里的最大最小值,需要分配的桶的数量,数组里的每个数与最小数的差值与计算的值( perBucket = (maxV - minV + bucketCount) // bucketCount)向下取整,得到一个值,为桶的索引,生成新的列表,列表里嵌套多个列表
- 每个桶内的元素,进行排序,规则是,遍历数组里的数,按插入排序规则,进行排序
- 桶是有顺序的,桶内的元素也是有顺序的,最终得到新的有序列表
时间复杂度分析
O(N^2)
最坏情况时间复杂度是O(N^2)
计数排序
1.8 计数排序 | 菜鸟教程 (runoob.com)
def CountingSort(aList):
n = len(aList)
countLen = max(aList) + 1
count = [0] * countLen
for val in aList:
count[val] += 1
print(count)
n = 0
for val in range(0, countLen):
while count[val] > 0:
count[val] -= 1
aList[n] = val
n += 1代码解读
- 创建一个数组,数组的长度为原列表中最大值+1
- 遍历列表,新数组对应的下标,在列表里查找到数,就进行计数+1
- 遍历新数组,当上一步的计数大于0时,计数-1,修改原列表的值,为新数组索引的值,每次索引+1
时间复杂度分析
O(n+k)
第一次遍历数组,时间复杂度:O(n),第二次遍历计数器,(如果有k个计数器)时间复杂度O(K),加起来,时间复杂度为:O(n+k)
基数排序
1.10 基数排序 | 菜鸟教程 (runoob.com)
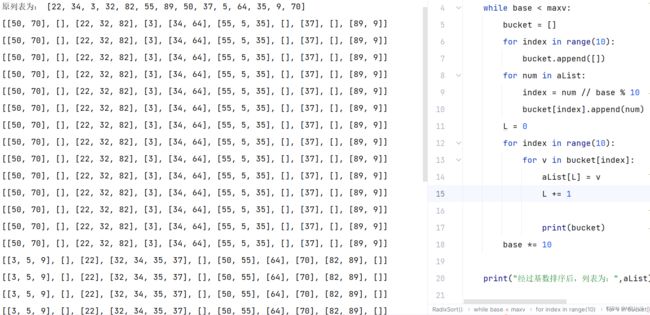
def RadixSort(aList):
base = 1
maxv = max(aList)
while base < maxv:
bucket = []
for index in range(10):
bucket.append([])
for num in aList:
index = num // base % 10
bucket[index].append(num)
L = 0
for index in range(10):
for v in bucket[index]:
aList[L] = v
L += 1
print(aList)
base *= 10代码解读
- 本质上也像前面的桶排序、计数排序一样,都用到了桶,计数排序:每个桶只存储单一键值;桶排序:每个桶存储一定范围的数值;基数排序:根据键值的每位数字来分配桶;
- 创建一个桶
- 遍历数组,将数据放入桶内
- 再从桶内将数据取出来
时间复杂度分析
O(n*k)
时间复杂度:O(n*k),其中n是输入元素的数量,k是数字的最大位数。
堆排序
1.7 堆排序 | 菜鸟教程 (runoob.com)
def maxHeapify(heap, start, end):
son = start * 2
while son <= end:
if son + 1 <= end and heap[son + 1] > heap[son]:
son += 1
if heap[son] > heap[start]:
heap[start], heap[son] = heap[son], heap[start]
start, son = son, son * 2
else:
break
def HeapSort(aList):
heap = [None] + aList
root = 1
L = len(heap)
for i in range(L // 2, root - 1, -1):
maxHeapify(heap, i, L - 1)
for i in range(L - 1, root, -1):
heap[i], heap[root] = heap[root], heap[i]
maxHeapify(heap, root, i - 1)
return heap[root:]代码解读
先来看看什么是堆,推荐阅读下面的这篇博客
大顶堆,小顶堆_这瓜保熟么的博客-CSDN博客
时间复杂度分析
建堆的时间复杂度为O(n),排序重建堆的时间复杂度为nlog(n),总的时间复杂度为O(nlogn)
总结
针对具体的序列,每种排序算法复杂度都不同,具体要用到哪种排序算法,要结合实际案例,针对每种算法的时间复杂度的分析和应用,后面再做一下总结,此外,每种排序算法的代码要加以理解巩固!多练习几遍排序算法,达到熟练使用的程度。“无他,唯手熟尔”!