【学习笔记】动态规划—各种 DP 优化
【大前言】
个人认为贪心,\(dp\) 是最难的,每次遇到题完全不知道该怎么办,看了题解后又瞬间恍然大悟(TAT)。这篇文章也是花了我差不多一个月时间才全部完成。
【进入正题】
用动态规划解决问题具有空间耗费大、时间效率高的特点,但也会有时间效率不能满足要求的时候,如果算法有可以优化的余地,就可以考虑时间效率的优化。
【DP 时间复杂度的分析】
\(DP\) 高时间效率的关键在于它减少了“冗余”,即不必要的计算或重复计算部分,算法的冗余程度是决定算法效率的关键。而动态规划就是在将问题规模不断缩小的同时,记录已经求解过的子问题的解,充分利用求解结果,避免了反复求解同一子问题的现象,从而减少“冗余”。
但是,一个动态规划问题很难做到完全消除“冗余”。
下面给出动态规划时间复杂度的决定因素:
时间复杂度 \(=\) 状态总数 \(×\) 每个状态转移的状态数 \(×\) 每次状态转移的时间
【DP 优化思路】
一:减少状态总数
\((1).\) 改进状态表示
\((2).\)选择适当的规划方向
二:减少每个状态转移的状态数
\((1).\) 四边形不等式和决策的单调性
\((2).\) 决策量的优化
\((3).\) 合理组织状态
\((4).\) 细化状态转移
三:减少状态转移的时间
\((1).\) 减少决策时间
\((2).\) 减少计算递推式的时间
(上述内容摘自 《动态规划算法的优化技巧》毛子青 ,想要深入了解其思想的可以去看看这篇写得超级好的论文。)
看到这里是不是已经感觉有点蒙了呢?
本蒟蒻总结了一个简化版本:
【DP 三要点】
在推导 \(dp\) 方程时,我们时常会感到毫无头绪,而实际上 \(dp\) 方程也是有迹可循的,总的来说,需要关注两个要点:状态,决策和转移。其中 “状态” 又最为关键,决策最为复杂。
【状态】
关于 “状态” 的优化可以从很多角度出发,思维难度及其高,有时候状态选择的好坏会直接导致出现暴零和满分的分化。
【决策】
与 “状态” 不同,“决策” 优化则有着大量模板化的东西,在各大书籍,文章上你都可以看到这样的话:只要是形如 \(XXX\) 的状态转移方程,都可以用 \(XXX\) 进行优化。
【转移】
“转移” 则指由最优决策点得到答案的转移过程,其复杂度一般较低,通常可以忽略,但有时也需要特别注意并作优化。
本文将会重点针对 “决策” 优化部分作一些总结,记录自己的感悟和理解。
\[ QAQ \]
一:【矩阵优化 DP】
【前言】
矩阵优化 \(dp\) 通常用于线性递推式的 \(dp\) 优化,能以优异的时间复杂度实现大量的状态转移。
其实质是优化 “转移”。
1.【题目特征】
\((1).\) 类似递推(划重点)
\((2).\) 转移次数 \(10^9\) 左右(雾)
\((3).\) 决策点较少(常数)
2.【前置芝士】
首先要清楚矩阵是个什么东西,在对 \(dp\) 进行优化时通常只会用矩阵乘法加速。
【矩阵乘法】
矩阵乘法的一般式:\(C_{i,j}=\sum (A_{i,k} \times B_{k,j})\),其中 \(A\) 为 \(N \times K\) 的矩阵,\(B\) 为 \(K*M\) 的矩阵,矩阵 \(A \times B\) 得到 \(N \times M\) 的矩阵 \(C\) 。
式子的含义为:矩阵 \(C_{i,j}\) 由矩阵 \(A\) 第 \(i\) 行上的 \(K\) 个数与矩阵 \(B\) 第 \(j\) 列上的 \(K\) 分别相乘并求和得到。
划重点:矩阵乘法满足结合律,不满足交换律,满足分配律
3.【如何优化加速】
以 斐波那契数列 \([P1962]\) 为例,大家应该都会简单的求 \(Fibonacci\),其递推式为 \(f(n)=f(n-1)+f(n-2) (n \geqslant 2\) \(且\) \(n \in N^{*})\),其中 \(f(1)=f(2)=1\) 。
这道题按照正常的递推做法可以过 \(60\) 分,对于大一点的 \(n\) 就不行了。
由于其递推方程是固定的,决策点只要两个(\(n-1\) 和 \(n-2\)),所以可以考虑用矩阵乘法加速。
【推出基本累乘矩阵】
还是以 斐波那契数列 \([P1962]\) 为例,
注意决策点数量:两个,可以先尝试使用二维矩阵,如果不行就试着加一维(一般来说不用加维),大概做法如下:
设 \(f(n)\) 为 \(Fibonacci\) 数列第 \(n\) 项。
先构建一个 \(1 \times 2\) 的答案矩阵 \(F(n)\):
\(F(n) = \begin{vmatrix}f(n)&f(n-1)\end{vmatrix}\)
再构造一个 \(2 \times 2\) 的累乘矩阵 \(base\):
\(base = \begin{vmatrix}a&b\\c&d\end{vmatrix}\),其中 \(a,b,c,d\) 均为未知数
我们需要满足:\(F(n) \times base = F(n+1)\) 。
即 \(\begin{vmatrix}f(n)&f(n-1)\end{vmatrix} \times \begin{vmatrix}a&b\\c&d\end{vmatrix} = \begin{vmatrix}af(n)+cf(n-1)&bf(n)+df(n-1)\end{vmatrix} = \begin{vmatrix}f(n+1)&f(n)\end{vmatrix}\)
即 \(af(n)+cf(n-1)=f(n+1),bf(n)+df(n-1)=f(n)\)
由递推式可知:\(a=b=c=1,d=0\)
即 \(base = \begin{vmatrix}1&1\\1&0\end{vmatrix}\)
【快速幂加速运算】
对 \(F(n)\) 稍作转换:\(F(n) = F(2) \times base \times base......\times base\),其中 \(base\) 一共乘了 \(n-2\) 次。
为什么要写 \(F(2)\) 呢?在写题时,这是一个致命的细节问题。
根据定义,\(F(1)=\begin{vmatrix}f(1)&f(0)\end{vmatrix}\),其中 \(f(0)\) 无法计算(或者说毫无意义),所以要用 \(f(2)\) 作为初始矩阵来计算。
由矩阵乘法结合律可知: \(F(n)=F(2) \times base^{n-2} = \begin{vmatrix}1&1\end{vmatrix} \times \begin{vmatrix}1&1\\1&0\end{vmatrix}^{n-2}\)
即 \(F(n) = \begin{vmatrix}1&1\end{vmatrix} \times \begin{vmatrix}1&1\\1&0\end{vmatrix}^{n-2} = \begin{vmatrix}f(n)&f(n-1)\end{vmatrix}\)
在具体的代码实现中,我们可以将 \(F(n)\) 视为 \(2 \times 2\) 的矩阵,多余的部分赋值为 \(0\),即 \(F(n) = \begin{vmatrix}f(n)&f(n-1)\\0&0\end{vmatrix}\),可以发现,不管怎么乘,它还是这样的形式(第二行和 \(1 \times 2\) 矩阵的变化相同,第二行依然全为 \(0\))。
求 \(base\) 的幂时用一个快速幂,注意快速幂初始值要设为 \(F(2)\),如果在算完 \(base^{n-2}\) 后再乘上 \(F(2)\) 的话,就违背了矩阵乘法不满足交换律的原则。
时间复杂度为 \(O(logn)\)。
4.【Code】
//f[1]=f[2]=1,f[n]=f[n-1]+f[n-2]
//[1 1]
//[1 0]
#include
#include
#define LL long long
const int P=1e9+7;
struct QAQ{//结构体打包用起来比较方便
LL a[3][3];
void CL(){memset(a,0,sizeof(a));a[1][1]=a[2][1]=a[1][2]=1;}
QAQ operator * (QAQ &x){
int i,j,k;QAQ ans;memset(ans.a,0,sizeof(ans.a));
for(i=1;i<3;i++)
for(j=1;j<3;j++)
for(k=1;k<3;k++)
(ans.a[i][j]+=a[i][k]*x.a[k][j]%P)%=P;
return ans;
}
};
LL n;
inline LL sovle(LL k){
if(k<1)return 1;//特判很重要
if(!k)return 1;
QAQ s,x;x.CL();s.a[1][1]=s.a[1][2]=1,s.a[2][1]=s.a[2][2]=0;//初始化F(2)
while(k){
if(k&1)s=(s*x);
x=(x*x);k>>=1;
}
return s.a[1][1]%P;
}
int main(){
scanf("%lld",&n);
printf("%lld\n",sovle(n-2));
} 5.【题目链接】
【简单题】
斐波那契数列 \([P1962]\)
【标签】递推/数论数学/矩阵乘法【模板】矩阵加速(数列)\([P1939]\)
【标签】递推/数论数学/矩阵乘法
【中档题】
- 小奇的集合 \([BZOJ4547]\) \([HDU5171]\)
【题解】「省选模拟赛」小奇的集合
\[ QAQ \]
二:【数据结构优化 DP】
【前言】
在一些 \(dp\) 方程的状态转移过程中,我们通常需要在某个范围内进行择优,选出最佳决策点,这往往可以作为 \(dp\) 优化的突破口。
数据结构的使用较灵活,没有一个特定的模板,需要根据具体情况而定,选择合适的方案。由于状态转移总是伴随着区间查询最值,区间求和等操作,即动态区间操作,所以平衡树可以作为一个有用的工具,但考虑到代码复杂度,使用树状数组或者线段树将会是一个不错的选择。。
其实质是优化 “决策”。
1.【维护合适的信息】
以 \(The\) \(Battle\) \(of\) \(Chibi\) \([UVA12983]\) 为例,大概题意就是计算在给定的序列中严格单调递增子序列的数量,并对 \(1e9 +7\) 取模,给定序列长度小于等于 \(1000\) 。
方程应该是比较好推的,用 \(dp[i][j]\) 表示由序列中在 \(j\) 之前的数构成并以 \(a[j]\) 结尾的子序列中,长度为 \(i\) 的子序列的数量。则:\(dp[i][j]=\sum dp[i-1][k]\) ,其中 \(k < j\) \(且\) \(a[k] < a[j]\) 。
对于决策点 \(dp[i-1][k]\) 这里出现了 \(3\) 个信息:
\((1).\) 在原序列中的位置 \(k
\((2).\) \(a[k]
\((3).\) \(dp[i-1][k]\) 的和。
对于 \((1)\),可以用枚举的顺序解决,剩下的两个信息即是数据结构需要维护的信息。
对于每一次 \(dp[i]\) 的决策,可以将 \(a[j]\) 作为数据结构维护的关键字, \(dp[i-1][j]\) 作为权值,加入 \(-inf\) 后离散化,得到一个大小为 \(N+1\) 的数组并在上面建立树状数组,每次计算 \(dp[i][j]\) 时查询前面已经加入的且关键字小于 \(a[j]\) 的 \(dp[i-1][k]\) 总和(即区间查询),然后把 \(dp[i-1][j]\) 加入树状数组(单点查询)。
时间复杂度为 \(O(logn)\)。
当问题涉及到的操作更复杂时,树状数组无法维护所需要的信息,就只有用线段树了。这道题较简单,所以选择了代码复杂度更低的树状数组。
2.【Code】
#include
#include
#include//UVA抽风,加上这个就好了
#include
#define Re register int
using namespace std;//UVA抽风,还要加这个
const int N=1005,P=1e9+7;
int n,m,T,k,ans,cnt,a[N],b[N],C[N],dp[N][N];
inline void add(Re x,Re v){while(x<=n+1)(C[x]+=v)%=P,x+=x&-x;}
inline int ask(Re x){Re ans=0;while(x)(ans+=C[x])%=P,x-=x&-x;return ans%P;}
int main(){
scanf("%d",&T);
for(Re o=1;o<=T;++o){
scanf("%d%d",&n,&m),ans=0,cnt=n;
memset(dp,0,sizeof(dp));
for(Re i=1;i<=n;++i)scanf("%d",&a[i]),b[i]=a[i],dp[1][i]=1;
sort(b+1,b+n+1);//离散
cnt=unique(b+1,b+n+1)-b-1;//去重
for(Re i=2;i<=m;++i){
memset(C,0,sizeof(C));//每次都要清空,重新开始维护
for(Re j=1;j<=n;++j)
dp[i][j]=ask((k=lower_bound(b+1,b+cnt+1,a[j])-b)-1),add(k,dp[i-1][j]);
}
for(Re j=1;j<=n;++j)(ans+=dp[m][j])%=P;
printf("Case #%d: %d\n",o,ans);
}
} 3.【题目链接】
【简单题】
- \(The\) \(Battle\) \(of\) \(Chibi\) \([UVA12983]\)
【 标签】动态规划/树状数组
【高档题】
方伯伯的玉米田 \([P3287]\)
【 标签】动态规划/二维树状数组基站选址 \([P2605]\)
【 标签】动态规划/线段树
\[ QAQ \]
三:【决策单调性】
【前言】
形如 \(dp[i]=min(dp[j]+w(j,i))\) \((L_i \leqslant j \leqslant R_i)\) 的 \(dp\) 方程被称作 \(1D/1D\) 动态规划,其中 \(L_i\) 和 \(R_i\) 单调递增,\(w(j,i)\) 决定着优化策略选择。
针对决策点具有的特性,可以大大降低寻找最优决策点的时间。
其实质是优化 “决策”。
1.【定义】
【决策单调性】
设 \(j_0[i]\) 表示 \(dp[i]\) 转移的最优决策点,那么决策单调性可描述为 \(\forall i \leqslant j,j_0[i] \leqslant j_0[j]\)。也就是说随着 \(i\) 的增大,所找到的最优决策点是递增态(非严格递增)。
【四边形不等式】
\(w(x,y)\) 为定义在整数集合上的一个二元函数,若 \(\forall a \leqslant b \leqslant c \leqslant d,w(a,c)+w(b,d) \leqslant w(a,d)+w(b,c)\),那么函数 \(w\) 满足四边形不等式。
为什么叫做四边形不等式呢?在 \(w(x,y)\) 函数的二维矩阵中挖一块四边形,左上角 加 右下角 小于等于 左下角 加 右上角。
2.【定理及其证明】
定理 (1):四边形不等式的另一种定义
\(w(x,y)\) 为定义在整数集合上的一个二元函数,若 \(\forall a < b,w(a,b)+w(a+1,b+1) \leqslant w(a+1,b)+w(a,b+1)\),那么函数 \(w\) 满足四边形不等式。
\(证明:\)
\(\because \forall a < c,w(a,c)+w(a+1,c+1) \leqslant w(a+1,c)+w(a,c+1)\)
\(\therefore \forall a+1 < c,w(a+1,c)+w(a+2,c+1) \leqslant w(a+2,c)+w(a+1,c+1)\)
\(上下两式相加,有:\) \(w(a,c)+w(a+2,c+1) \leqslant w(a,c+1)+w(a+2,c)\)
\(以此类推\) \(\forall a \leqslant b\leqslant c,w(a,c)+w(b,c+1) \leqslant w(a,c+1)+w(b,c)\)
\(同理\) \(\forall a \leqslant b \leqslant c \leqslant d,w(a,c)+w(b,d) \leqslant w(a,d)+w(b,c)\)
定理 (2):决策单调性
\(1D/1D\) 动态规划具有决策单调性当且仅当函数 \(w\) 满足四边形不等式 时成立。
\(证明:\)
\(\because\) \(j_0[i]\) \(在\) \(dp[i]\) \(的决策点中最优\)
\(\therefore\) \(\forall i \in [1,N],\forall j \in [0,j_0[i]-1],dp[j_0[i]]+w(j_0[i],i) \leqslant dp[j]+w(j,i)\)
\(易知\) \(\forall i' \in [i+1,N]\),\(均满足\) \(j
\(又\) \(\because\) \(函数\) \(w\) \(满足四边形不等式\)
\(\therefore\) \(w(j,i)+w(j_0[i],i') \leqslant w(j,i')+w(j_0[i],i)\)
\(移项得:\) \(w(j_0[i],i')-w(j_0[i],i) \leqslant w(j,i')-w(j,i)\)
\(与第一个式子相加,有:\) \(dp[j_0[i]]+w(j_0[i],i') \leqslant dp[j]+w(j,i')\)
最后的式子含义是:把 \(j_0[i]\) 作为 \(dp[i']\) 的决策点,一定比小于 \(j_0[i]\) 的任意一个 \(j\) 都要更好。也就是说,\(dp[i’]\) 的最优决策点不可能小于 \(j_0[i]\) ,即 \(j_0[i'] \geqslant j_0[i]\),所以方程 \(dp\) 具有决策单调性。
3.【证明决策单调性】
这里以 玩具装箱 \(toy\) \([P3195]\) 为例(因为这个比较好证 QAQ),先来证一波决策单调性。
设 \(S[n]=\sum _{i=1}^n (C[i]+1)\),用 \(dp[i]\) 表示装好前 \(i\) 个的最小花费,则 \(dp\) 方程为:\(dp[i]=min(dp[j]+(S[i]-S[j]-1-L)^2)\)。
很明显,这个方程是一个 \(1D/1D\) 动态规划方程,其中 \(w(i,j)=(S[i]-S[j]-1-L)^2\)。
(注意在四边形不等式中的 \(j\) 不是 \(i\) 决策点,可以理解为 \(i’\)。而 \(w(i,j)\) 的值可以理解为是由已完成的状态 \(dp[i]\) 转移到 \(dp[j]\) 所带有的附加价值)。
\(证明:设\) \(Q=S[i]-S[j]-1-L\)
\(\therefore w(i,j)=(S[i]-S[j]-1-L)^2=Q^2\)
\(\begin{equation*} \begin{split} \therefore w(i+1,j+1)=&(S[i+1]-S[j+1]-1-L)^2\\ =&((S[i]+C[i+1]+1)-(S[j]+C[j+1]+1)-1-L)^2\\ =&(Q+C[i+1]-C[j+1])^2 \end{split} \end{equation*}\)
\(\begin{equation*} \begin{split} w(i,j+1)=&(S[i]-S[j+1]-1-L)^2\\ =&(S[i]-(S[j]+C[j+1]+1)-1-L)^2\\ =&(Q-C[j+1]-1)^2 \end{split} \end{equation*}\)
\(\begin{equation*} \begin{split} w(i+1,j)=&(S[i+1]-S[j]-1-L)^2\\ =&((S[i]+C[i+1]+1)-S[j]-1-L)^2\\ =&(Q+C[i+1]+1)^2 \end{split} \end{equation*}\)
\(\therefore w(i,j)+w(i+1,j+1)=2X^2+2C[i+1]X-2C[j+1]X+C[i+1]^2-2C[i+1]C[j+1]+C[j+1]^2\)
\(\therefore w(i+1,j)+w(i,j+1)=2X^2+2C[i+1]X-2C[j+1]X+C[i+1]^2+2C[i+1]+2C[j+1]+C[j+1]^2+2\)
\(\therefore w(i,j)+w(i+1,j+1)-w(i+1,j)+w(i,j+1)=-2(C[i+1]+1)(C[j+1]+1)\)
\(又 \because C[i],C[j] \geqslant 1\)
\(\therefore -2(C[i+1]+1)(C[j+1]+1) \leqslant -8\)
\(\therefore w(i,j)+w(i+1,j+1) \leqslant w(i+1,j)+w(i,j+1)\)
由定理 \((1)\) 可知,函数 \(w\) 满足四边形不等式。
又由定理 \((2)\)可知, 方程 \(dp\) 具有决策单调性。
在实战中,通常使用打表的形式来验证 \(w\) 函数的递变规律。
4.【实现方法】
关于决策单调性和斜率优化这两个东西的分类似乎有争议,有人说斜优是决策单调性的一种(好像就是二分栈来着?),也有人说斜优是针对斜率进行优化,是决策单调性是其一种方案(你谷某管理大大),我支持前一种说法。
(\(ps.\) 对于此处及以下语言不严谨处,大家可以认真思考并给予建议,待日后对其理解加深后再行修改。)
这里选择不同的例题将二者分开讲。
【二分栈】
二分栈,顾名思义就是二分加栈。
用栈维护单调的决策点,二分找到最优决策点。
以 \(Lightning\) \(Conductor\) \([P3515]\) 为例,题目大意就是在给定长度为 \(n\) 的序列 \(a\) 中,对于每一个 \(i\),找到最小的自然数 \(p_i\) 满足对于任意的 \(j \in [1,n]\),均有 \(a_j \leqslant a_i+p_i-\sqrt{\left|i-j\right|}\) 。
把这个式子变下形:\(p_i \geqslant a_j-a_i+\sqrt{\left|i-j\right|}\) 。
即 \(p_i=max \{ a_j+\sqrt{\left|i-j\right|} \} -a_i\)
即 \(p_i = max \{ max\{a_j+\sqrt{i-j}\}(j \in [1,i]),max\{a_j+\sqrt{j-i}\}(j \in [i+1,n]) \}-a_i\)
可以发现里面两个 \(max\) 可以视为同一个问题(只要把序列翻转一下就可以了),所以只需要考虑求出对于每一个 \(i\) 的 \(max\{ a_j+\sqrt{i-j} \}\),其中 \(j \in [1,i]\)。
设 \(y_j=a_j+\sqrt{i-j}\)
那么我们会得到 \(n\) 个关于 \(i\) 函数,\(p_i=max\{ y_j \}\)。
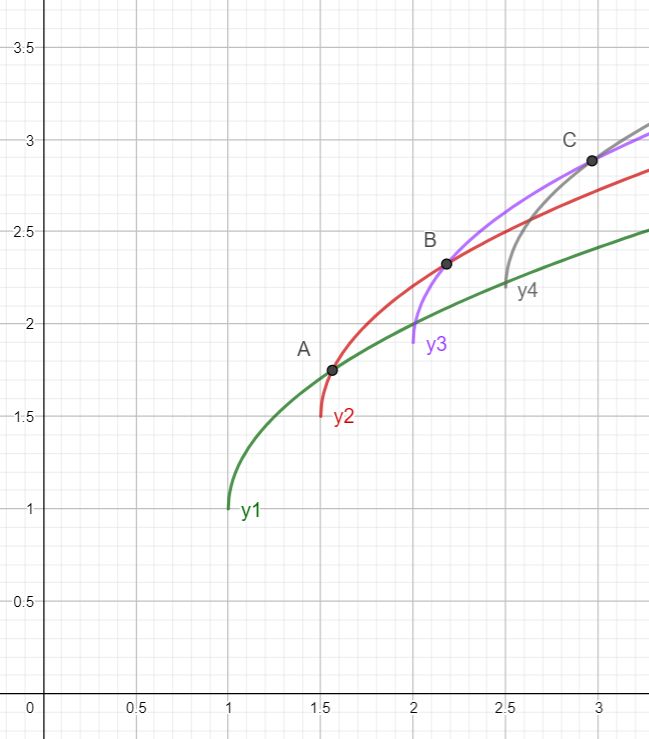
可知当 \(i=4\) 时,直线 \(x=4\) 与 \(y1=a_1+\sqrt{x-1}\) 的交点即为 \(p_4\)。
在上图中,对于任意 \(j \in [1,n]\) ,\(y1\) 总是在最上面,也就是说下面的其他函数可以踢掉不要,但由于 \(sqrt\) 函数的增速递减,会出现如图中 \(y2,y4\) 的情况,即存在一个交点使得在该点两边时两条直线的位置关系不同。此时如果没有上面的 \(y1\),\(y2,y4\) 都有可能成为答案,所以不能乱踢。
设 \(k_1\) 为 \(y_1,y_2\) 的交点,\(k_2\) 为 \(y_2,y_3\) 的交点。
此时 \(k_1 > k_2\),可以发现 \(y_2\) 始终在其他直线的下面,可以放心的将其踢掉。
对于不同的 \(i\) 来说,都有一个互不不同的直线在最上方,所以该决策集合里的直线都是有用的。可以从图中看出,最优决策点单调递增(决策单调性的数学证明较麻烦,本人能力不足,不作探讨)。
维护决策集合用单调队列,查找直线交点用二分,随便搞搞就行了。
时间复杂度为 \(O(nlogn)\)。
【分治】
为方便描述,用 \(dp[a,b]\) 表示 \(dp[a],dp[a+1],dp[a+2]...dp[b]\)。
假设我们已知 \(dp[l,r]\) 的最优决策点均位于 \([L,R]\),再设 \(dp[mid]\) 的最优决策点为 \(j_0\),其中 \(mid=(l+r)/2\)。根据决策单调性的定义可知:
\(dp[l,mid-1]\) 的最优决策点位于 \([L,k]\),
\(dp[mid+1,r]\) 的最优决策点位于 \([k,R]\)。
原问题变成了两个规模更小的同类型问题,所以可以用分治来对 \(dp\) 进行优化。
分治的话理解和代码都要简单一些,但在某些情况下可能要被卡,时间复杂度会严重退化,所以还是二分栈的实用性更高。
还是以 \(Lightning\) \(Conductor\) \([P3515]\) 为例,每次的分治中先暴力扫一遍找到 \(p[mid=(l+r)/2]\) 的最优决策点 \(j_0\),然后做一下左边,再做一下右边,然后 \(...\) 然后 \(...\) 就没了。
时间复杂度为 \(O(nlogn)\)。
5.【Code】
二分栈
#include
#include
#include
#define Re register int
using namespace std;
const int N=5e5+3;
int i,j,n,h,t,a[N],Q[N],Poi[N];
double p[N],sqr[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline double Y(Re i,Re j){return a[j]+sqr[i-j];}
inline int find_Poi(int j1,int j2){//找到两个直线的交点i
Re l=j2,r=n,mid,ans=n+1;//为了处理两个直线没有交点的情况,用一个变量记录答案
while(l<=r){
mid=l+r>>1;
if(Y(mid,j1)<=Y(mid,j2))ans=mid,r=mid-1;
//当前这个位置i使得直线j1的纵坐标小于直线j2的纵坐标,说明这个点i在交点的右方,所以右边界要缩小
else l=mid+1;
}
return ans;
}
inline void sakura(){
h=1,t=0;
for(i=1;i<=n;++i){//由于i本身也是一个决策点,所以要先入队再取答案择优
while(h=find_Poi(Q[t],i))--t;//如果出现了上述可踢的情况,出队
Poi[t]=find_Poi(Q[t],i),Q[++t]=i;
while(h 分治
#include
#include
#include
#define Re register int
using namespace std;
const int N=5e5+3;
int i,j,n,h,t,a[N],Q[N],Poi[N];
double tmp,p[N],sqr[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
inline void sakura(Re l,Re r,Re L,Re R){
if(l>r)return;
Re mid=l+r>>1,j0;double mx=0;
for(Re j=L;j<=mid&&j<=R;++j)
//暴力找p[i]的最优决策点j0,而其决策点j必须满足j<=i,即此处的j<=mid
if((tmp=a[j]+sqr[mid-j])>mx)mx=tmp,j0=j;
p[mid]=max(p[mid],mx);
sakura(l,mid-1,L,j0),sakura(mid+1,r,j0,R);
}
int main(){
in(n);
for(Re i=1;i<=n;++i)in(a[i]),sqr[i]=sqrt(i);
sakura(1,n,1,n);
for(Re i=1;i 6.【题目链接】
【中档题】
\(Lightning\) \(Conductor\) \([P3515]\)
【标签】动态规划/决策单调性\(Noi\) 嘉年华 \([P1973]\)
【标签】动态规划/决策单调性大佬 \([P3724]\)
【标签】动态规划/决策单调性
【高档题】
- 诗人小 \(G\) \([P1912]\)
【标签】动态规划/单调队列/贪心
\[ QAQ \]
四:【单调队列优化 DP】
【前言】
形如 \(dp[i]=max/min \{ dp[j]+funtion(i)+function(j) \}\) 的 \(dp\) 方程均可尝试使用单调队列优化。
单调栈和单调队列给我们展现出了一种思想:在保证正确性的前提下,及时排除不可能的决策点,保持决策集合内部的有序性和查找决策的高效性。之前的二分栈,此处的单调队列优化,和后面的斜率优化都是以此为核心来运作的。
其实质是优化 “决策”。
1.【单调队列的简单运用】
【T1】
琪露诺 \([P1725]\)(盗版滑动窗口QAQ)。
【题目大意】
在给定序列中找出一条路径使其经过的点之和最大,且每次可走的距离在给定区间 \([l,r]\) 以内。
【分析】
方程非常简单:\(dp[i]=max\{ dp[j]+a[i] \} (i-r \leqslant j \leqslant i-l)\) 。
在某一次决策中,由于决策点 \(j\) 只可能在 \([i-l,i-r]\) 这一段区间内,可以只将这些点放入决策集合。
而 \(l,r\) 是定值,当 \(i\) 不断增大时,之前小于 \(i-l\) 的 \(j\) 现在还是小于 \(i-l\),所以可以永远地踢掉。
若 \(j < j'\) 且 \(dp[j] \leqslant dp[j']\),那么 \(dp[j]\) 也可以永远地踢掉。为什么呢? \(j\) 在 \(j'\) 的前面,一定会先成为不合法决策点,而 \(j\) 的价值又比 \(j'\) 小,因此留下来只是浪费扫描的时间。
最终维护出了一个价值递减的单调队列。
【Code】
#include
#include
#include
#define Re register int
using std::max;
const int N=2e5+3;
int n,l,r,h=1,t,a[N],Q[N];
long long ans=-2e9,dp[N];
inline void in(Re &x){
int f=0;x=0;char c=getchar();
while(c<'0'||c>'9')f|=c=='-',c=getchar();
while(c>='0'&&c<='9')x=(x<<1)+(x<<3)+(c^48),c=getchar();
x=f?-x:x;
}
int main(){
in(n),in(l),in(r);
memset(dp,-127,sizeof(dp));
Q[++t]=0;
for(Re i=0;i<=n;++i)in(a[i]);
dp[0]=a[0];
for(Re i=l;i<=n;i++){//注意枚举起点是l不是1
while(h<=t&&dp[Q[t]]<=dp[i-l])--t;//维护单调递减
Q[++t]=i-l;//入队
while(h<=t&&Q[h]=n-r)ans=max(ans,dp[i]);
}
printf("%lld",ans);
} 【T2】
\(fence\) \([POJ1821]\)
【题目大意】
\(M\) 个工人要对 \(N\) 块木板进行粉刷。工人 \(i\) 要么不刷,要么就刷不超过 \(L_i\) 块并且包含 \(S_i\) 的连续一段木板,每粉刷一块木板有 \(P_i\) 的报酬。要求使总报酬最大。
【分析】
\(S_i\) 的散乱分布非常讨厌,所以先把工人按 \(S_i\) 排个序。
主要信息有“工人序号”,“木板序号”,“报酬”这三个,而其中“报酬”为所求答案,可以用 \(dp[i][j]\) 表示前 \(i\) 个工人刷完前 \(j\) 块木板所得总报酬。
考虑状态转移:
第 \(i\) 个工人可以跳过不刷木板,也可以跳过第 \(j\) 块木板不刷,因此先在 \(dp[i-1][j]\) 和 \(dp[i][j-1]\) 当中取个最大值。
工人 \(i\) 想要粉刷的区间 \([k+1,j]\) 必须包括 \(S_i\),并且区间长度要小于等于 \(L_i\)。
所以得出 \(dp\) 转移方程:\(dp[i][j]=max \{ dp[i-1][j],dp[i][j-1],dp[i-1][k]+P_i*(j-k) \}\),其中 \(S_i \leqslant j\) 且 \(k \in [j-L_i,S_i-1]\)。
\(k\) 为决策点,\(P_i*j\) 为定值可以单独提出来,所以实际上就是上面琪露诺 \([P1725]\)一样的类型,只是加了一维而已。
最终维护出了一个 \(dp[i-1][k]-P_i*k\) 递减的单调队列。
【Code】
#include
#include
#include
#define Re register int
using namespace std;
const int N=16005;
struct QAQ{int L,P,S;}a[105];
int n,m,i,j,k,Q[N],W[N],dp[105][N];
inline bool cmp(QAQ a,QAQ b){return a.Sj&&j>=Si){//Si+Li-1>=j>=Si
while(l<=r&&W[l]+Li 2.【单调队列优化多重背包】
先来回顾一下多重背包问题。
用 \(v,w,c\) 分别表示物品重量,价值,数量,\(n\) 为物品数量,\(V\) 为背包容量。\(dp\) 方程为:\(dp[j]=max\{ dp[j-k*v[i]]+k*w[i] \} (j \in [v[i],V],k \in [1,min(c[i],j/v[i])])\)
还可以用二进制拆分来进行优化,但就是有这样一道题,连 \(log\) 都要卡:多重背包 \([CodeVS5429]\)。所以还需要考虑更高效的算法。
但说来说去似乎都和单调队列扯不上关系。
为何?
观察 \(dp[j]\) 和 \(dp[j-1]\) 决策集合:
\(dp[j]: \{ j \% v[i]...j-2*v[i],j-v[i] \}\)
\(dp[j-1]: \{ (j-1) \% v[i]...(j-1)-2*v[i],(j-1)-v[i] \}\)
\(dp[j]\) 的每一个决策点都与 \(dp[j-1]\) 不同,很难根据 \(dp[j-1]\) 的决策集合转移成 \(dp[j]\) 的决策集合。
再看 \(dp[j]\) 和 \(dp[j-v[i]]\):
\(dp[j]: \{ j-c[i]*v[i]...j-2v[i],j-v[i] \}\)
\(dp[j-v[i]]: \{ j-(c[i]+1)*v[i]...j-3v[i],j-2v[i] \}\)
可以发现上面只是比下面的区别仅仅在于 \(j-(c[i]+1)*v[i]\) 和 \(j-v[i]\) ,恰好满足单调队列的一个特性:但有新的决策出现时,决策点集合中会去掉一部分不合法的,再加上一部分新来的。
所以我们可以按照 \(j%v[i]\) 的余数来分一下:
\(dp[j](j\%v[i]=0):\{0,v[i],2v[i]...j-2v[i],j-v[i]\}\)
\(dp[j](j\%v[i]=1):\{1,v[i]+1,2v[i]+1...j-2v[i],j-v[i] \}\)
\(...\)
\(dp[j](j\%v[i]=v[i]-1):\{v[i]-1,2v[i]-1...j-2v[i],j-v[i]\}\)
设 \(j=p*v[i]+r\),那么原方程可改为: \(dp[p*v[i]+r]=max\{ dp[r+k*v[i]]+(p-k)*w[i] \} (r \in [0,v[i]-1],p \in [1,\lfloor(V-r)/v[i]\rfloor],k \in [p-min( \lfloor V/w[i]\rfloor ,c[i]),p])\)
只要在最外层将 \(i,r,p\) 都枚举出来,这就是一个标准的单调队列可优化方程,用类似 \(fence\) \([POJ1821]\) 的方法维护即可。
时间复杂度为 \(O(N*V)\) 。
【Code】
#include
#define Re register int
const int N=7003,M=7003;
int n,h,t,V,mp,tmp,v[N],w[N],c[N],Q[N],K[N],dp[M];
inline void in(Re &x){
Re fu=0;x=0;char ch=getchar();
while(ch<'0'||ch>'9')fu|=ch=='-',ch=getchar();
while(ch>='0'&&ch<='9')x=(x<<1)+(x<<3)+(ch^48),ch=getchar();
x=fu?-x:x;
}
inline int max(Re a,Re b){return a>b?a:b;}
inline int min(Re a,Re b){return amin(c[i],V/v[i]))++h;
dp[p*v[i]+r]=max(dp[p*v[i]+r],Q[h]+p*w[i]);
}
}
printf("%d",dp[V]);
} 3.【题目链接】
【简单题】
- 琪露诺 \([P1725]\)
【标签】动态规划/单调队列
【中档题】
\(fence\) \([POJ1821]\)
【标签】动态规划/单调队列多重背包 \([CodeVS5429]\)
【标签】动态规划/单调队列/多重背包我要长高 \([UESTC594]\)
【标签】动态规划/单调队列
\[ QAQ \]
五:【斜率优化 DP】
由于篇幅过大,已搬出。。。。。
【学习笔记】动态规划—斜率优化DP(超详细)
补充:其实质是优化 “决策”。
\[ QAQ \]
【参考文献】
(本文部分内容摘自以下文章)
凸包—百度百科
\(dp\) 的各种优化
决策单调性优化
斜率优化学习笔记
斜率优化及其变形
斜率优化\(dp\)及总结
四边形不等式优化
四边形不等式学习笔记
四边形不等式优化讲解(详解)
单调队列优化的多重背包
动态规划的单调队列优化(含多重背包)
题解 \([P3195]\) 玩具装箱
题解 \([P1962]\) 斐波那契数列
\(dp\) 基础 — \(DraZxINDdt\)
《算法竞赛进阶指南》李煜东
《动态规划算法的优化技巧》毛子青