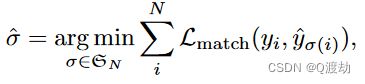使用transformers进行端到端的目标检测

目录

目标检测的旧方法

使用transformers进行端到端的目标检测

抛去了目标检测旧的方法

网络架构

Transformer encoder

Transformers and Parallel Decoding

注意力起到的作用

使用Hungarian algorithm算法完成匹配

在使用transformers的端到端目标检测中，匈牙利算法被应用于处理目标检测的预测结果和真实标签之间的匹配问题。该算法帮助确定预测框与真实框之间的最佳匹配，并将它们关联起来

---

目标检测的旧方法

（1）、fast-rcnn系列，各种proposal方法

（2）、YOLO系列，都是基于anchor这种方式

（3）、NMS那也一定用的上，输出结果肯定要过滤一下

使用transformers进行端到端的目标检测

抛去了目标检测旧的方法

“Our approach streamlines the detection pipeline, effectively removing the need for many hand-designed components like a non-maximum suppression procedure or anchor generation that explicitly encode our prior knowledge about the task.” (Carion 等, 2020, p. 1)

网络架构

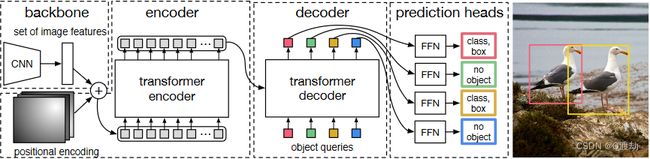
“The overall DETR architecture is surprisingly simple and depicted in Figure 2. It contains three main components, which we describe below: a CNN backbone to extract a compact feature representation, an encoder-decoder transformer, and a simple feed forward network (FFN) that makes the final detection prediction.” (Carion 等, 2020, p. 6)

Transformer encoder

“First, a 1x1 convolution reduces the channel dimension of the high-level activation map f from C to a smaller dimension d. creating a new feature map z0 ∈ Rd×H×W . The encoder expects a sequence as input, hence we collapse the spatial dimensions of z0 into one dimension, resulting in a d×HW feature map. Each encoder layer has a standard architecture and consists of a multi-head self-attention module and a feed forward network (FFN). Since the transformer architecture is permutation-invariant, we supplement it with fixed positional encodings [31,3] that are added to the input of each attention layer. We defer to the supplementary material the detailed definition of the architecture, which follows the one described in [47].” (Carion 等, 2020, p. 6)

首先降低通道数，将得到的三维数据变成一维数据，变成序列数据，然后输入到编码器中

也就是说Encoder完成的任务是得到各个目标的注意力结果（只关注自己需要关注的部分），准备好特征，等待解码器来选

Transformers and Parallel Decoding

“We also combine transformers and parallel decoding for their suitable trade-off between computational cost and the ability to perform the global computations required for set prediction” (Carion 等, 2020, p. 4) 我们还将变压器和并行解码结合起来，以便在计算成本和执行集合预测所需的全局计算能力之间进行适当的权衡

object queries是核心，让它学会如何从原始特征中找到物体的位置

注意力起到的作用

即使目标物体之间遮挡很严重，照样可以学习（注意颜色）

所以使用注意力机制可以很好地解决目标重叠问题

使用Hungarian algorithm算法完成匹配

匈牙利算法（Hungarian algorithm），也被称为Kuhn-Munkres算法，是一种用于解决最佳分配问题的优化算法。它被广泛应用于任务分配、资源分配、最大化利润等问题。

算法的主要目标是在一个二维矩阵中找到一组元素，使得每一行和每一列中的元素都只能在选定的组合中出现一次，并且这组元素的和达到最大或最小。

以下是匈牙利算法的详细步骤：

1. 创建原始二维矩阵，其中包含待分配任务/资源的成本或收益。

2. 对于二维矩阵的每一行，找到最小值，并在每一行中将该最小值减去。

3. 对于二维矩阵的每一列，找到最小值，并在每一列中将该最小值减去。

4. 遍历二维矩阵中的每个零元素，将每个零元素的行和列标记为“已访问”。

5. 如果找到一组已访问的行和列，使得它们的零元素形成一个完美匹配（即每一行和每一列只有一个标记的零元素），则此时已找到最佳的分配。如果找不到，将进行下一步。

6. 标记未访问的行。

7. 将已访问的列中的零元素关联到已标记的行，并尝试通过调整标记来形成更多的完美匹配。

8. 重复步骤5-7，直到找到最佳的分配。

通过执行以上步骤，匈牙利算法能够找到最佳任务分配或资源分配，使得成本最小化或收益最大化

在使用transformers的端到端目标检测中，匈牙利算法被应用于处理目标检测的预测结果和真实标签之间的匹配问题。该算法帮助确定预测框与真实框之间的最佳匹配，并将它们关联起来

1. 首先，通过目标检测网络对输入图像进行前向传播，得到预测框的边界框坐标和类别概率。

2. 接下来，我们获取真实标签中的边界框信息和类别。

3. 创建一个二维矩阵，其中的行表示预测框，列表示真实框，矩阵的每个元素表示两个框之间的匹配得分。匹配得分可以根据预测框与真实框之间的IoU（交并比）计算得到。

4. 对于矩阵的每一行，使用匈牙利算法找到与该行对应的最佳匹配，即在每一行找到与当前预测框具有最大IoU的真实框，并将其匹配得分记录下来。

5. 接着，在矩阵的每一列中，找到与该列对应的最佳匹配，即在每一列找到与当前真实框具有最大IoU的预测框，并将其匹配得分记录下来。

6. 然后，根据前面找到的最佳匹配，使用最小权匹配算法将矩阵中的其余元素设置为负无穷。这样可以确保每个预测框和真实框都只被匹配一次。

7. 最后，根据匈牙利算法得到的最佳匹配，将预测框和真实框进行关联，形成最终的目标检测结果。匹配得分较高的预测框和真实框之间建立关联，从而得到目标检测中的最佳匹配。

通过使用匈牙利算法，我们可以在端到端的目标检测中得到最佳的预测框与真实框的匹配，提高检测算法的准确性和鲁棒性。这种匹配方式可以将预测框与真实框进行关联，进而进行目标的检测和识别