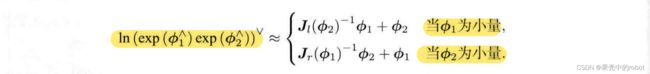【SLAM数学基础】李群与李代数 & BCH近似公式

三维旋转构成了三维旋转群 SO(3)，其对应的李代数为 $\mathfrak{so}$(3)；三维变换构成了三维变换群 SE(3)，其对应的李代数为 $\mathfrak{se}$(3)。

1.指数映射

李代数元素到李群元素的映射为指数映射，其中 $\mathfrak{so}$(3) 至 SO(3) 的指数映射为：

$$\exp ({\mathbf{\varphi }}^{\wedge })=\mathbf{R}=\text{Exp}(\mathbf{\varphi })$$

具体计算公式由罗德里格斯公式给出：

$$\mathbf{R}=\cos \theta \cdot \mathbf{I}+(1-\cos \theta )\mathbf{n}{\mathbf{n}}^T+\sin \theta \cdot {\mathbf{n}}^{\wedge }=\exp ({\mathbf{\varphi }}^{\wedge })$$

其中 $\mathbf{\varphi }\in \mathfrak{so}(3)$ 可以分解为 $\mathbf{\varphi }=\theta \mathbf{n}$.

2.对数映射

从李群元素到李代数元素的映射为对数映射，记作

$$\mathbf{\varphi }=\log (\mathbf{R}{)}^{\vee }=\text{Log}(\mathbf{R})$$

其中$\mathbf{\varphi }\in \mathfrak{so}(3)$ 可以分解为 $\mathbf{\varphi }=\theta \mathbf{n}$，具体的计算过程由下式给出：

$$\begin{gathered} \theta =\arccos \left(\frac{tr(\mathbf{R})-1}{2}\right) \\ \mathbf{R}\mathbf{n}=\mathbf{n} \end{gathered}$$

其中 转轴 $\mathbf{n}$ 是矩阵 $R$ 特征值1对应的单位特征向量。

3. BCH公式及其线性近似表达

两个李代数指数映射乘积的完整形式，由 Baker-Campbell-Hausdorff 公式（BCH公式）给出，其展开式的前几项为：

$$\ln \left(\exp (A)\exp (B)\right)=A+B+\frac{1}{2}[A,B]+\frac{1}{12}[A,[A,B]]-\frac{1}{12}[B,[A,B]]+\cdots$$

其中 [ ] 为李括号。特别地，考虑 SO(3) 上的李代数 $\ln {\left(\exp ({\mathbf{\varphi }}_1^{\wedge })\exp ({\mathbf{\varphi }}_2^{\wedge })\right)}^{\vee }$，当 ${\mathbf{\varphi }}_1$ 或 ${\mathbf{\varphi }}_2$ 为小量时，小量二次以上的项可以忽略，此时 BCH 具有线性近似表达：

第一个近似公式表明，当对一个旋转矩阵 ${\mathbf{R}}_2$(李代数为 ${\mathbf{\varphi }}_2$) 左乘一个微小旋转矩阵 ${\mathbf{R}}_1$(李代数为 ${\mathbf{\varphi }}_1$)时，可以近似看作在原来的李代数 ${\mathbf{\varphi }}_2$ 加上了一项 ${\mathbf{J}}_l({\mathbf{\varphi }}_2{)}^{-1}{\mathbf{\varphi }}_1$。同理，第二个近似公式描述了右乘一个微小旋转的情况。

因此，李代数在BCH近似下分成了左乘和右乘近似两种，使用时需要注意区分。

4. SO(3)上的BCH近似公式

BCH公式给出了李代数上的小量加法与李群上小量乘法之间的关系（李代数加法 $\iff$ 李群乘法），其线性近似公式广泛应用于各种函数的线性化。

在SO(3)中，某个旋转 $\mathbf{R}$ 对应的李代数为 $\mathbf{\varphi }$，左乘一个微小旋转，记作 $\Delta \mathbf{R}$，对应的李代数为 $\Delta \mathbf{\varphi }$，那么在李群上得到的结果就是 $\Delta \mathbf{R}\mathbf{R}$，而在李代数上，根据BCH近似，为 ${\mathbf{J}}_l(\mathbf{\varphi }{)}^{-1}\Delta \mathbf{\varphi }+\mathbf{\varphi }$，合并后可以简单写成：

$$\Delta \mathbf{R}\mathbf{R}=\exp (\Delta {\mathbf{\varphi }}^{\wedge })\exp ({\mathbf{\varphi }}^{\wedge })=\exp \left((\mathbf{\varphi }+{\mathbf{J}}_l(\mathbf{\varphi }{)}^{-1}\Delta \mathbf{\varphi }{)}^{\wedge }\right)$$

反过来，如果在李代数上进行加法，让一个 $\mathbf{\varphi }$ 加上小量 $\Delta \mathbf{\varphi }$，那么可以近似为李群上带左右雅克比矩阵的乘法：

$$\exp ((\mathbf{\varphi }+\Delta \mathbf{\varphi }{)}^{\wedge })=\exp (({\mathbf{J}}_l(\mathbf{\varphi })\Delta \mathbf{\varphi }{)}^{\wedge })\exp ({\mathbf{\varphi }}^{\wedge })=\exp ({\mathbf{\varphi }}^{\wedge })\exp (({\mathbf{J}}_r(\mathbf{\varphi })\Delta \mathbf{\varphi }{)}^{\wedge })$$

其中SO(3)的左雅克比矩阵为

$$\begin{gathered} {\mathbf{J}}_l(\theta \mathbf{a})=\frac{\sin \theta }{\theta }\mathbf{I}+(1-\frac{\sin \theta }{\theta })\mathbf{a}{\mathbf{a}}^T+(\frac{1-\cos \theta }{\theta }){\mathbf{a}}^{\wedge } \\ {\mathbf{J}}_l^{-1}(\theta \mathbf{a})=\frac{\theta }{2}\cot \frac{\theta }{2}\mathbf{I}+(1-\frac{\theta }{2}\cot \frac{\theta }{2})\mathbf{a}{\mathbf{a}}^T-\frac{\theta }{2}{\mathbf{a}}^{\wedge } \end{gathered}$$

而SO(3)的右雅克比矩阵为

$${\mathbf{J}}_r(\mathbf{\varphi })={\mathbf{J}}_l(-\mathbf{\varphi })$$

值得注意的是，由于李代数 $\mathbf{\varphi }$ 可以和旋转矩阵 $\mathbf{R}$ 简单地对应起来，因此有时也把 ${\mathbf{J}}_r(\mathbf{\varphi })$ 简单地记作 ${\mathbf{J}}_r(\mathbf{R})$ 而不是 ${\mathbf{J}}_r(\text{Log}(\mathbf{R}))$。另外，在很多情况下，也会省略 ${\mathbf{J}}_r(\mathbf{\varphi })$ 括号里的内容，而直接记为 ${\mathbf{J}}_r$ 和 ${\mathbf{J}}_l$，这都是为了让公式看上去更加简洁。

参考教程

1. 自动驾驶与机器人中的SLAM技术：从理论到实践/高翔著. —北京：电子工业出版社，2023.8
2. 视觉SLAM十四讲：从理论到实践/高翔等著.— 2版. —北京：电子工业出版社，2019.9