机器学习（监督学习）笔记

笔记内容

代码部分

#  实验2-1
# 批梯度下降
import pandas as pd
import numpy as np
import random as rd 
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
xuexi = 0.0001 # 学习率
ep = 20
epoch = [ep] # 遍历次数
m =  np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集
    a = rd.choice(alls) # 从alls中随机选取一个
    trainsyo.append(y0[a]) # 增加训练集标注
    trainsy14.append(y14[a])#  增加训练集输入特征
    alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
#     global y0
#     global y14
    testyo.append(y0[a])# 增加测试集标注
    testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE = [] # 均方根误差
RMSE2  = [] # 训练集
while(epoch[0]): # 开始遍历
    epoch[0]  -=  1 # 设置的超参数epoch -1
    e =np.dot(testy14,w.transpose()) + b[0] - testyo
    RMSE.append((np.dot(e,e.transpose())/tes)**0.5)
    e = np.dot(trainsy14,w.transpose()) + b[0] - trainsyo # n*1
    RMSE2.append((np.dot(e,e.transpose())/tra)**0.5)
    b[0] -= 2*xuexi*np.dot(np.ones(tra),e)/tra
    w -= 2*xuexi*np.dot(e.transpose(),trainsy14)/tra
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标 
print(min(RMSE),min(RMSE2))
ymax = max(RMSE) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',marker='o',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([0,ep+ 1,0,ymax]) # 设置xy的取值范围
plt.show() # 展示图片

# 2-2
import pandas as pd
import numpy as np
import random as rd 
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[3] for i in data])# 选第三维作为输入特征
xuexi = 0.0001 # 学习率
ep = 20
epoch = [ep] # 遍历次数
m =  np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
allw = [] # 训练过程中的全部的w
allb = [] # 训练过程中的全部的b
for i in range(tra): # 获取训练集
    a = rd.choice(alls) # 从alls中随机选取一个
    trainsyo.append(y0[a]) # 增加训练集标注
    trainsy14.append(y14[a])#  增加训练集输入特征
    alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
#     global y0
#     global y14
    testyo.append(y0[a])# 增加测试集标注
    testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(1)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE = [] # 均方根误差
while(epoch[0]): # 开始遍历
    epoch[0]  -=  1 # 设置的超参数epoch -1
    newb = 0 # 求解的b的值
    newW = int() # 求解的w的值
    for i in range(tra): # 遍历全部的训练集
        a = np.dot(w,trainsy14[i].transpose()) + b[0] - trainsyo[i] # 计算(W*xT + b - y )
        newb += float(a) # 累加
        if type(newW) == int: 
            newW = trainsy14[i].transpose()*float(a) # 初次赋值
        else:
            newW += trainsy14[i].transpose()*float(a) # 累加w
    w -= xuexi*newW * (2/tra) # 更新w
    b[0] -= xuexi*newb *2 / tra # 更新b
    allw.append(w[0])
    allb.append(b[0])
yall = []
xs= [-5,-3,--1,0,1,3,5] # x 轴模板
xall = [xs for i in range(ep)]
ymax = 0
ymin = 30
for i in range(ep):
    yall.append([allw[i]*t + allb[i] for t in xs])
    ymax = max(ymax,max(yall[i]))
    ymin  = min(ymin,min(yall[i]))
#绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标 
plt.xlabel('x') # 设置x坐标名称
plt.ylabel('y') # 设置y坐标名称
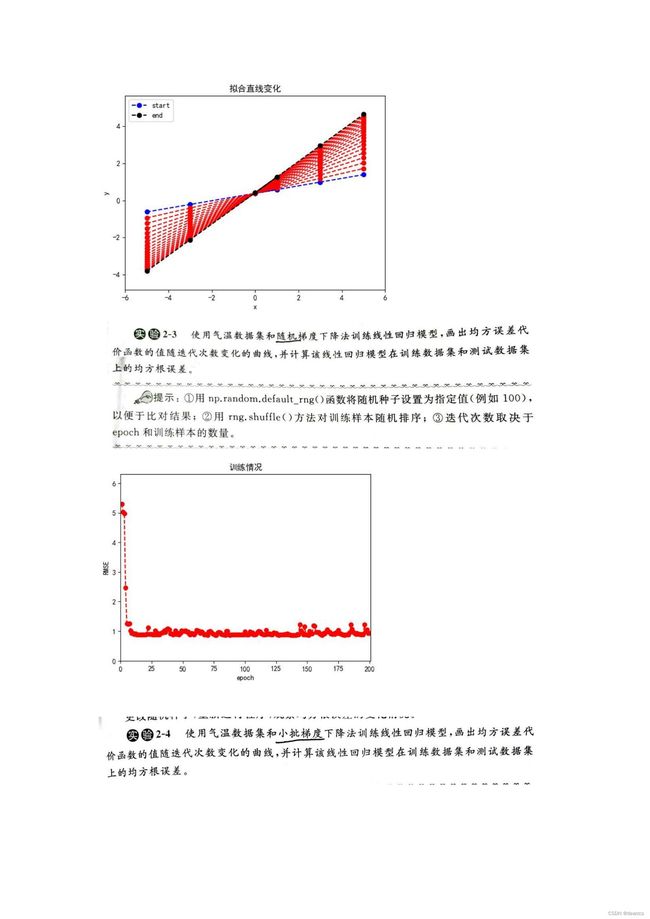
plt.title('拟合直线变化') # 设置标题
plots = []
for i in range(ep):
    c='r'
    if i == 0:
        c = 'b'
    elif i == ep -1:
        c = 'k'
    p, = plt.plot(xall[i],yall[i],color=c,marker='o',linestyle='dashed')
    plots.append(p)
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.legend((plots[0],plots[-1]),['start','end'])
plt.axis([-6,6,ymin-1,ymax+1]) # 设置xy的取值范围
plt.show() # 展示图片

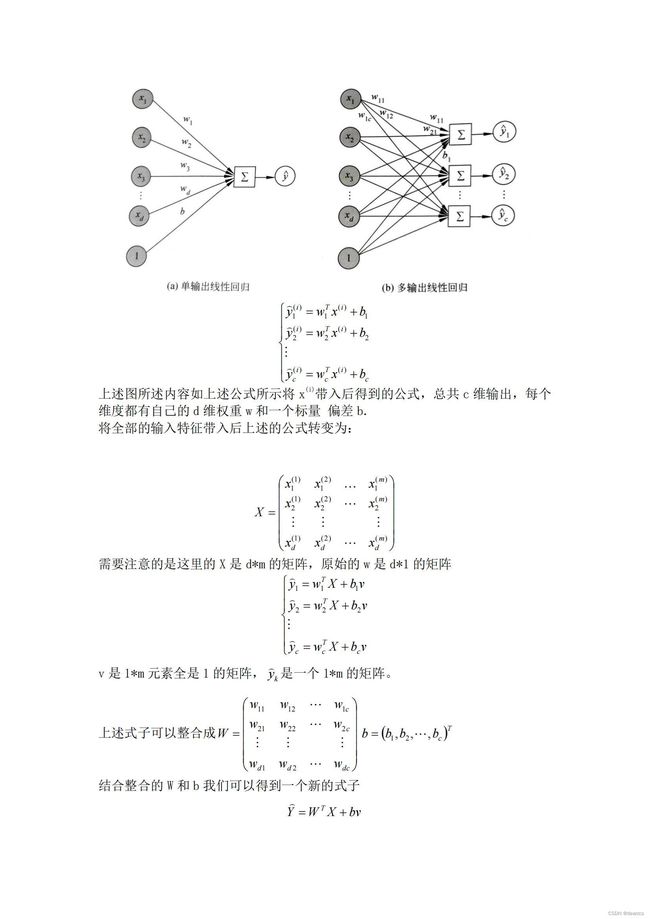
# 2-3
# 随机梯度下降
import pandas as pd
import numpy as np
import random as rd 
import matplotlib.pyplot as plt
# load dataset
np.random.seed(100)
rng = np.random.default_rng()
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
xuexi = 0.0001 # 学习率
ep = 200
epoch = [ep] # 遍历次数
m =  np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集
    a = rd.choice(alls) # 从alls中随机选取一个
    trainsyo.append(y0[a]) # 增加训练集标注
    trainsy14.append(y14[a])#  增加训练集输入特征
    alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
#     global y0
#     global y14
    testyo.append(y0[a])# 增加测试集标注
    testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE = [] # 均方根误差
while(epoch[0]): # 开始遍历
    epoch[0]  -=  1 # 设置的超参数epoch -1
    newtra = [i for i in range(tra)]
    rd.shuffle(newtra)
    i = rd.choice(newtra)
    a = np.dot(w,trainsy14[i].transpose()) + b[0] - trainsyo[i] # 计算(W*xT + b - y )
    b[0] -=  2*xuexi*a
    w  -= 2*xuexi*trainsy14[i].transpose()*a # 初次赋值
    y = 0 # 中间变量用于存储RMSE每一轮的
    for i in range(tes): # 
        y += (np.dot(w,testy14[i].transpose()) + b[0] - testyo[i])**2 # 计算均方根误差，并累加 
    RMSE.append((y/tes)**0.5)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标 
print(min(RMSE))
ymax = max(RMSE) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',marker='o',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([0,ep+ 1,0,ymax]) # 设置xy的取值范围
plt.show() # 展示图片

# 2-4
# 小批梯度下降
import pandas as pd
import numpy as np
import random as rd 
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
xuexi = 0.0001 # 学习率
batch = 30 # 设置批长度
ep = 20 # 设置遍历次数
epoch = [ep] # 遍历次数
m =  np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集
    a = rd.choice(alls) # 从alls中随机选取一个
    trainsyo.append(y0[a]) # 增加训练集标注
    trainsy14.append(y14[a])#  增加训练集输入特征
    alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
#     global y0
#     global y14
    testyo.append(y0[a])# 增加测试集标注
    testy14.append(y14[a]) # 增加测试集输入特征
w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
# print(w)
b = [rd.random()] # 初次随机获取偏差b
RMSE2 = []
RMSE = [] # 均方根误差
while(epoch[0]): # 开始遍历
    epoch[0]  -=  1 # 设置的超参数epoch -1
    if not batch:break
    times = tra // batch
    if tra % batch:
        times += 1
    for _ in range(times):
        starts = _*batch
        ends = (_+1)*batch
        if (_+1)*batch >= tra:
            ends = tra
            batch = tra%batch
            if(not batch):break
        e =np.dot(testy14,w.transpose()) + b[0] - testyo
        RMSE.append((np.dot(e,e.transpose())/tes)**0.5)
        e = np.dot(trainsy14[starts:ends],w.transpose()) + b[0] - trainsyo[starts:ends] # n*1
        RMSE2.append((np.dot(e,e.transpose())/batch)**0.5)
        b[0] -= 2*xuexi*np.dot(np.ones(batch),e)/batch
        w -= 2*xuexi*np.dot(e.transpose(),trainsy14[starts:ends])/batch
# 绘图部分
print(min(RMSE))
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(20)] # 设置x坐标 
RMSE = RMSE[:20]
ymax = max(RMSE[:20]) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',marker='o',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([-2,len(RMSE)+ 6,0,ymax+3]) # 设置xy的取值范围
plt.show() # 展示图片

#2-5 
# 各种标准化
import pandas as pd
import numpy as np
import random as rd 
import matplotlib.pyplot as plt
# load dataset
df = pd.read_csv('temperature_dataset.csv')
data = np.array(df)
y0 = np.array([i[0] for i in data]) # 第一列作为样本标注
y14 = np.array([i[1:] for i in data])#2-5 作为四维输出特征
# 标准化
# mean = np.mean(y14,0) # 平均值
# stds = np.std(y14,0,ddof=1)
# y14 = (y14-mean)/stds
# 最小最大归一化
# maxs = np.amax(y14,0)
# mins = np.amin(y14,0)
# y14 = (y14 - mins)/(maxs-mins)
# 均值归一化
mean = np.mean(y14,0) # 平均值
maxs = np.amax(y14,0)
mins = np.amin(y14,0)
y14 = (y14-mean)/(maxs - mins)
xuexi = 0.1 # 学习率
ep = 2000
epoch = [ep] # 遍历次数
m =  np.size(data,0) # 获取样本长度 m
alls = [i for i in range(m)]
trainsyo = [] # 训练集标注
testyo = [] # 测试集标注
trainsy14 = [] # 训练集输入特征
testy14 = [] # 测试集输入特征
tra = int(m * 0.8) # 训练集长度
tes = m - tra # 测试集长度
for i in range(tra): # 获取训练集
    a = rd.choice(alls) # 从alls中随机选取一个
    trainsyo.append(y0[a]) # 增加训练集标注
    trainsy14.append(y14[a])#  增加训练集输入特征
    alls.remove(a)
trainsy14 = np.array(trainsy14) # 训练集list转变array
trainsyo = np.array(trainsyo) # 训练集list转变array
for a in alls: # 获取测试集
    testyo.append(y0[a])# 增加测试集标注
    testy14.append(y14[a]) # 增加测试集输入特征
# w = np.array([rd.random() for i in range(4)]) # 初次随机获取权重w
w =np.array([0.,0.,0.,0.])
# print(w)
# b = [rd.random()] # 初次随机获取偏差b
b = [0.]
RMSE = [] # 均方根误差
RMSE2 = [] # 训练集均方根误差
while(epoch[0]): # 开始遍历
    epoch[0]  -=  1 # 设置的超参数epoch -1
    e =np.dot(testy14,w.transpose()) + b[0] - testyo
    RMSE.append((np.dot(e,e.transpose())/tes)**0.5)
    e = np.dot(trainsy14,w.transpose()) + b[0] - trainsyo # n*1
    RMSE2.append((np.dot(e,e.transpose())/tra)**0.5)
    b[0] -= 2*xuexi*np.dot(np.ones(tra),e)/tra
    w -= 2*xuexi*np.dot(e.transpose(),trainsy14)/tra
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
x = [i+1 for i in range(ep)] # 设置x坐标 
print(min(RMSE),min(RMSE2))
ymax = max(RMSE) + 1
plt.xlabel('epoch') # 设置x坐标名称
plt.ylabel('RMSE') # 设置y坐标名称
plt.title('训练情况') # 设置标题
plt.plot(x,RMSE,color='r',linestyle='dashed')
plt.plot(x,RMSE2,color='k',linestyle='dashed')
# plt.plot(x,RMSE,color='r') # 设置绘图的基本参数
plt.axis([0,ep+ 1,0,ymax]) # 设置xy的取值范围
plt.show() # 展示图片

# 2-8
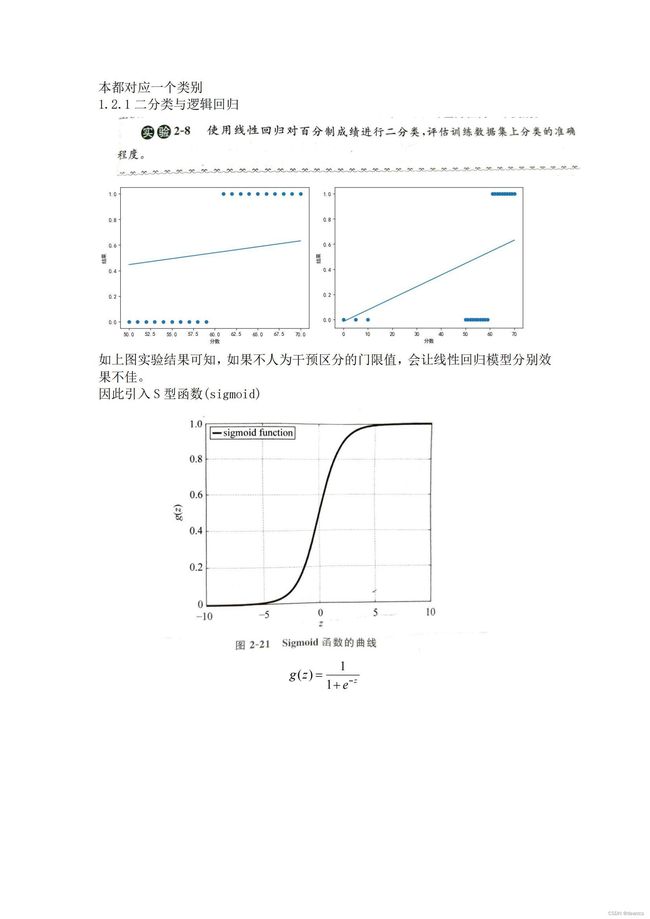
# 线性回归对百分制成绩进行二分类
import numpy as np
import matplotlib.pyplot as plt
import random as rd
# parameters
dataset = 2 # index of training dataset
epoch = 2000
sdy = 0.0001
# datasets for training
if dataset == 1: # balanced dataset
    x_train = np.array([50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70]).reshape((1, -1))
    y_train = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
elif dataset == 2: # unbalanced dataset 1
    x_train = np.array([0, 5, 10, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70]).reshape((1, -1))
    y_train = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
elif dataset == 3: # unbalanced dataset 2
    x_train = np.array([0, 5, 10, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73]).reshape((1, -1))
    y_train = np.array([0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
m_train = x_train.size # number of training examples
w = np.array([0.]).reshape((1, -1))# 权重
b = np.array([0.])# 偏差
# 批梯度下降
for _  in range(epoch):
    e = np.dot(w,x_train) + b - y_train
#     print(e)
    b -= 2*sdy*np.dot(e,np.ones(m_train))/m_train
    w -= 2*sdy*np.dot(x_train,e.transpose())/m_train
# 画图部分
yc = []
yy = []
lines = w[0][0]*60 + b[0] 
for i in x_train[0]:
    datas = w[0][0]*i + b[0]
    yy.append(datas)
    yc.append( 1 if datas >=  lines  else 0)
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
plt.xlabel('分数')
plt.ylabel('结果')
plt.plot(x_train[0],yy)
plt.scatter(x_train[0],yc)
plt.show()
    

# 2-9
# 均方误差代价函数->逻辑回归模型
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
# load dataset
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
y4 = np.array([i[5:] for i in data]) # 标注
y03 = np.array([i[:5] for i in data]) # 4维输入特征
# 标准化
mean = np.mean(y03,0) # 平均值
stds = np.std(y03,0,ddof=1) # 标准差
y03 = (y03-mean)/stds# 标准化完成
# 学习率
xuexi = 0.1
# 训练次数
epoch = 30000
# 区分训练集和测试集
m = len(data) # 样本总长度
__ = [i for i in range(m)]
tram = int(m*0.7) # 训练集长度
tesm = m - tram # 测试集长度
trainx = [] # 训练集输入特征
trainy = [] # 训练集标注
testx = [] # 测试集输入特征
testy = [] # 测试集标注
# 开始随机筛选训练集
for i in range(tram):
    _ = rd.choice(__)
    trainx.append(y03[_])
    trainy.append(y4[_])
    __.remove(_)
# 剩下的样本就是 测试集合
for i in __:
    testx.append(y03[i])
    testy.append(y4[i])
trainx,trainy,testx,testy= np.array(trainx),np.array(trainy),np.array(testx),np.array(testy) # list => np.array
# 设置权重w，和偏差b
w = np.array([0.,0.,0.,0.,0.]).reshape(1,-1)
b = np.array([0.]).reshape(1,-1)
REMS = []
for _ in range(epoch):
    y = -(np.dot(w,trainx.transpose()) + b) # -wTx + b,1*n
    y = 1/(1 + np.exp(y)) # 计算1/(1+e(-(wTx+b)))1*n 
    e = y - trainy.transpose() # 计算 e  1*n
    w -= 2*xuexi*np.dot((y*(1-y)*e),trainx)/tram # 1*4 # 更新w
    b -= 2*xuexi*np.dot((y*(1-y)),e.transpose()) / tram # 更新b
    # 测试集REMS 计算
    y = -(np.dot(w,testx.transpose()) + b) # -wTx + b,1*n 
    y = 1/(1 + np.exp(y)) # 1*n 
    e = y - testy.transpose() # 1*n
    a = np.dot(e,e.transpose())[0][0]/tesm
    REMS.append(a**0.5)

    # 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
x = [i for i in range(epoch)]
print(min(REMS))
plt.plot(x,REMS,color='b',linestyle='dashed')
plt.xlabel('epoch')
plt.ylabel('REMS')
plt.title('训练情况')
plt.show()

# 3D图像展示2-9
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
# load dataset
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
y4 = np.array([i[5:] for i in data]) # 标注
y03 = np.array([i[:1] for i in data]) # 1维输入特征
# 标准化
mean = np.mean(y03,0) # 平均值
stds = np.std(y03,0,ddof=1) # 标准差
y03 = (y03-mean)/stds# 标准化完成
# 学习率
xuexi = 0.1
# 训练次数
epoch = 1000
# 区分训练集和测试集
m = len(data) # 样本总长度
__ = [i for i in range(m)]
tram = int(m*0.7) # 训练集长度
tesm = m - tram # 测试集长度
trainx = [] # 训练集输入特征
trainy = [] # 训练集标注
testx = [] # 测试集输入特征
testy = [] # 测试集标注
# 开始随机筛选训练集
for i in range(tram):
    _ = rd.choice(__)
    trainx.append(y03[_])
    trainy.append(y4[_])
    __.remove(_)
# 剩下的样本就是 测试集合
for i in __:
    testx.append(y03[i])
    testy.append(y4[i])
trainx,trainy,testx,testy= np.array(trainx),np.array(trainy),np.array(testx),np.array(testy) # list => np.array
# 设置权重w，和偏差b
w = np.array([10.]).reshape(1,-1)
b = np.array([0.]).reshape(1,-1)
REMS = []
Wchange=[] # w的变化过程
Bchange=[] # B的变化过程
for _ in range(epoch):
    y = -(np.dot(w,trainx.transpose()) + b) # -wTx + b,1*n
    y = 1/(1 + np.exp(y)) # 计算1/(1+e(-(wTx+b)))1*n 
    e = y - trainy.transpose() # 计算 e  1*n
    w -= 2*xuexi*np.dot((y*(1-y)*e),trainx)/tram # 1*4 # 更新w
    b -= 2*xuexi*np.dot((y*(1-y)),e.transpose()) / tram # 更新b
    # 测试集REMS 计算
    y = -(np.dot(w,testx.transpose()) + b) # -wTx + b,1*n 
    y = 1/(1 + np.exp(y)) # 1*n 
    e = y - testy.transpose() # 1*n
    a = np.dot(e,e.transpose())[0][0]/tesm
    REMS.append(a**0.5)
    Wchange.append(w[0][0])
    Bchange.append(b[0][0])

    # 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig = plt.figure()
ax = fig.add_subplot(111, projection='3d')
Wchange, Bchange=np.meshgrid(Wchange,Bchange)
_ = REMS[:]
REMS = np.array([_ for i in range(epoch)])
# 绘制3D曲面图
ax.plot_surface(Bchange, Wchange, REMS, cmap='viridis')

# 设置图形属性
ax.set_xlabel('X Label')
ax.set_ylabel('Y Label')
ax.set_zlabel('Z Label')
ax.set_title('3D Surface Plot')

# 显示图形
plt.show()

# 实验2-10
# 交叉熵代价函数
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
# 基本参数确定
epoch = 10000
xuexi = 0.1
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(1)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
train_m = int(len(data)*split_rate)
test_m = len(data) - train_m
d = len(data[0])-1 # 输入特征维度（从0开始计数）
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d]  = (data[:,0:d]-mean)/stds
# 制作训练集和测试集
print(type(data))
train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
print(data[:train_m,0:d].shape)
# 初始化权重w和偏差b
w ,b= np.random.rand(1,d),np.random.rand(1,1)
Data = []
def Confusion_matrix(a,b): # 计算召回率，精度，F!分数的函数
    b = b > 0.5
    allp = np.sum(b)
    c = a*b
    TP = np.sum(c)
    FP = np.sum(a*(1-c))
#     FN = np.sum(b*(1-c))
#     TN = train_m - FP-allp
    R = TP/allp
    P = TP/(FP+TP)
    return R,P,2/(1/R + 1/P)
for _A_ in range(epoch):
    # 利用代价函数更新 w和 b
    e = -(np.dot(w,train_X.transpose())+ b)
    e = 1/(1 + np.exp(e)) 
    e -=  train_Y.transpose() # 1*train_m
    w -= xuexi*np.dot(e,train_X)/train_m
    b -= xuexi*np.dot(e,np.ones(train_m).transpose())/train_m
    # 计算交叉熵和召回率，精度以及F1分数
    # 训练集
    e = -(np.dot(w,train_X.transpose())+ b)
    N_Y = 1/(1 + np.exp(e))
    J = np.dot(np.log(N_Y),train_Y) +np.dot(np.log(1-N_Y),(1-train_Y)) 
    R,P,F1 = Confusion_matrix(N_Y>=0.5,train_Y[:].transpose())
    _ = {"R":R,"P":P,"F1":F1,'J1':-J[0][0]/train_m}
    # 测试集
    e =  -(np.dot(w,test_X.transpose())+ b)
    N_Y = 1/(1 + np.exp(e))
    J = np.dot(np.log(N_Y),test_Y) +np.dot(np.log(1-N_Y),(1-test_Y))
    _['J2'] = -J[0][0]/test_m
    _['R1'],_['P1'],_['F11'] = Confusion_matrix(N_Y>=0.5,test_Y[:].transpose())
    Data.append(_)
# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig, axes = plt.subplots(2, 2)
x = [i for i in range(epoch)]
axes[0][0].plot(x,[i['J1'] for i in Data],color='r',linestyle='dashed',label='train')
axes[0][0].plot(x,[i['J2'] for i in Data],color='b',linestyle='dashed',label='test')
axes[0][0].legend()
axes[0][0].set_title('交叉熵')
axes[0][1].plot(x,[i['P'] for i in Data],color='r',linestyle='dashed',label='train')
axes[0][1].plot(x,[i['P1'] for i in Data],color='b',linestyle='dashed',label='test')
axes[0][1].legend()
axes[0][1].set_title('精度')
axes[1][0].plot(x,[i['F1'] for i in Data],color='r',linestyle='dashed',label='train')
axes[1][0].plot(x,[i['F11'] for i in Data],color='b',linestyle='dashed',label='test')
axes[1][0].set_title('F1分数')
axes[1][0].legend()
axes[1][1].plot(x,[i['R'] for i in Data],color='r',linestyle='dashed',label='train')
axes[1][1].plot(x,[i['R1'] for i in Data],color='b',linestyle='dashed',label='test')
axes[1][1].set_title('召回率')
axes[1][1].legend()
plt.tight_layout()
plt.show()

# 2-11
# scikit-learn支持向量机
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
from sklearn import svm
# 基本参数确定
epoch = 10000
xuexi = 0.1
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(1)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
train_m = int(len(data)*split_rate)
test_m = len(data) - train_m
d = len(data[0])-1 # 输入特征维度（从0开始计数）
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d]  = (data[:,0:d]-mean)/stds
data[:,d:] = data[:,d:]+(data[:,d:]-1) # 将标注0改为1
# 制作训练集和测试集
train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
Call = [0.1,1,10,100,1000]
kernels = ['linear','poly','rbf']
data=[["线性核"],["多项式核"],["高斯核"]]
for i in Call:
    for j in kernels:
        clf = svm.SVC(C=i, kernel=j) #linear 线性核函数 poly 多项式核函数，rbf高斯径向基核函数（默认）
        clf.fit(train_X, train_Y.ravel())
        te = clf.predict(test_X)-test_Y.ravel()
        ta = clf.predict(train_X)-train_Y.ravel()
        te*=te
        ta*=ta
        te = int(np.sum(te))//4
        ta = int(np.sum(ta))//4
        data[kernels.index(j)].append("%d(%d+%d)"%(te+ta,ta,te))
#         print("C=%f  核函数：%s %d(%d+%d)"%(i,j,te+ta,ta,te))
# 表格绘制
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
# print(data)
fig, ax = plt.subplots()
ax.axis('off')  # 隐藏坐标轴

# 创建表格，设置文本居中
table = ax.table(cellText=data, colLabels=['核函数', 'C=0.1', 'C=1', 'C=10', 'C=100', 'C=1000'], cellLoc='center', loc='center')

# 设置表格样式
table.auto_set_font_size(False)
table.set_fontsize(14)
table.scale(1.2, 1.2)  # 放大表格

plt.show()

# 2-12
# 错误随c的变化
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
from sklearn import svm
# 基本参数确定
epoch = 10000
xuexi = 0.1
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(1)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
train_m = int(len(data)*split_rate)
test_m = len(data) - train_m
d = len(data[0])-1 # 输入特征维度（从0开始计数）
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d]  = (data[:,0:d]-mean)/stds
data[:,d:] = data[:,d:]+(data[:,d:]-1) # 将标注0改为1
# 制作训练集和测试集
train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
Call =list(np.random.uniform(0.1, 16, 150))
Call.sort()
kernels = ['linear','poly','rbf']
tadata=[[],[],[]]
tedata=[[],[],[]]
for i in Call:
    for j in kernels:
        clf = svm.SVC(C=i, kernel=j) #linear 线性核函数 poly 多项式核函数，rbf高斯径向基核函数（默认）
        clf.fit(train_X, train_Y.ravel())
        te = clf.predict(test_X)-test_Y.ravel()
        ta = clf.predict(train_X)-train_Y.ravel()
        te*=te
        ta*=ta
        te = int(np.sum(te))//4
        ta = int(np.sum(ta))//4
        tadata[kernels.index(j)].append(ta)
        tedata[kernels.index(j)].append(te)
# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig, axes = plt.subplots(2, 2)
x =Call
axes[0][0].plot(x,tadata[0],color='r',label='train',marker='x')
axes[0][0].plot(x,tedata[0],color='b',label='test',marker='o')
axes[0][0].legend()
axes[0][0].set_title('线性核')
axes[0][1].plot(x,tadata[1],color='r',label='train',marker='x')
axes[0][1].plot(x,tedata[1],color='b',label='test',marker='o')
axes[0][1].legend()
axes[0][1].set_title('多项式核')
axes[1][0].plot(x,tadata[2],color='r',label='train',marker='x')
axes[1][0].plot(x,tedata[2],color='b',label='test',marker='o')
axes[1][0].legend()
axes[1][0].set_title('高斯核心')
axes[1, 1].axis('off')# 隐蔽第四个
plt.tight_layout()
plt.show()

# 2-13
# k交叉验证 错误随c的变化
import matplotlib.pyplot as plt
import pandas
import numpy as np
import random as rd
from sklearn import svm
# 基本参数确定
epoch = 10000
xuexi = 0.1
k = 4 # 重交叉验证k的值
# 加载数据
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
rng = np.random.default_rng(100)
rng.shuffle(data)
# 训练集和测试集长度确定
split_rate = 0.7
alllines  = len(data)
train_m = int(alllines*((k-1)/k))
test_m = alllines - train_m
d = len(data[0])-1 # 输入特征维度（从0开始计数）
# 标准化
mean = np.mean(data[:train_m,0:d],0) # 平均值
stds = np.std(data[:train_m,0:d],0,ddof=1)# 标准差
data[:,0:d]  = (data[:,0:d]-mean)/stds
data[:,d:] = data[:,d:]+(data[:,d:]-1) # 将标注0改为1
# 制作训练集和测试集
# train_X,train_Y, test_X,test_Y= data[:train_m,0:d],data[:train_m,d:],data[train_m:,0:d], data[train_m:,d:]
Call =list(np.random.uniform(0.1, 10, 25))
Call.sort()
kernels = ['linear','poly','rbf']
tadata=[[],[],[]]
tedata=[[],[],[]]
for i in Call:
    for j in kernels:
        tadata1=[]
        tedata1=[]
        id = kernels.index(j)
        for t in range(k):
            start = t*test_m
            ends = (t+1)*test_m if ((t+1)*test_m ) <= alllines else alllines
            if t == 0:
                train_X,train_Y= data[ends:alllines,0:d],data[ends:alllines,d:]
            elif t == 3:
                train_X,train_Y= data[0:start,0:d],data[0:start,d:]
            else:
                 train_X,train_Y= np.concatenate((data[0:start,0:d],data[ends:alllines,0:d]),0),np.concatenate((data[0:start,d:],data[ends:alllines,d:]),0)
            test_X,test_Y=data[start:ends,0:d], data[start:ends:,d:]
            clf = svm.SVC(C=i, kernel=j) #linear 线性核函数 poly 多项式核函数，rbf高斯径向基核函数（默认）
            clf.fit(train_X, train_Y.ravel())
            te = clf.predict(test_X)-test_Y.ravel()
            ta = clf.predict(train_X)-train_Y.ravel()
            te*=te
            ta*=ta
            te = int(np.sum(te))//4
            ta = int(np.sum(ta))//4
            tadata1.append(ta)
            tedata1.append(te)
        tadata[id].append(sum(tadata1)/k)
        tedata[id].append(sum(tedata1)/k)
# 绘图部分
plt.rcParams['font.sans-serif'] = ['SimHei']  # 用来正常显示中文标签
plt.rcParams['axes.unicode_minus'] = False  # 用来正常显示负号
fig, axes = plt.subplots(2, 2)
x =Call
axes[0][0].plot(x,tadata[0],color='r',label='train',marker='x')
axes[0][0].plot(x,tedata[0],color='b',label='test',marker='o')
axes[0][0].legend()
axes[0][0].set_title('线性核')
axes[0][1].plot(x,tadata[1],color='r',label='train',marker='x')
axes[0][1].plot(x,tedata[1],color='b',label='test',marker='o')
axes[0][1].legend()
axes[0][1].set_title('多项式核')
axes[1][0].plot(x,tadata[2],color='r',label='train',marker='x')
axes[1][0].plot(x,tedata[2],color='b',label='test',marker='o')
axes[1][0].legend()
axes[1][0].set_title('高斯核心')
axes[1, 1].axis('off')# 隐蔽第四个
plt.tight_layout()
plt.show()

# 2-14
# 经典求解 k近邻
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
data=data.astype(np.float64)
# 随机排序
rng = np.random.default_rng(400)
rng.shuffle(data)
# 输入特征维度
d = data.shape[1] - 1
# 数据最大最小归一化处理
maxs = np.amax(data[:,0:d],0)
mins = np.amin(data[:,0:d],0)
data[:,0:d] = (data[:,0:d] - mins) / (maxs - mins)
# 样本长度
lens = data.shape[0]
# 设置k交叉验证中 k的值
k = 4
# 测试集长度
test_m = lens // k
# k近邻分类 中的k值
kk = [i for i in range(1,21)]
Error = [[],[]]
for i in kk:
    ta = 0
    te = 0
    for j in range(k):
        # 区分训练集和测试集
        start = j*test_m
        ends = (j+1)*test_m if (j != k-1) else lens
        if j == 0:
            train_x,train_y = data[ends:,0:d],data[ends:,d:]
        elif j == k -1:
            train_x,train_y = data[0:start,0:d],data[0:start,d:]
        else:
            train_x,train_y=np.concatenate((data[0:start,0:d],data[ends:,0:d]),0),np.concatenate((data[0:start,d:],data[ends:,d:]),0)
        test_x,test_y = data[start:ends,0:d],data[start:ends,d:]
        # 计算距离
        ans = 0 # 测试集错误率 
        for t in range(len(test_x)):
            _ = np.sum((train_x-test_x[t])*(train_x-test_x[t]),1)# 得到全部的距离
            __ = np.argsort(_) # 排序
            for h in range(i, len(_)):
                if _[__[h]] != _[__[h-1]]:
                    break
            _ = [train_y[hh] for hh in __[:h]]
            if test_y[t]  != stats.mode(_,keepdims=False)[0][0]:
                ans += 1
        te += ans
#         print(ans)
         # 计算距离
        ans = 0 # 测试集错误率 
        for t in range(len(train_x)):
            _ = np.sum((train_x-train_x[t])*(train_x-train_x[t]),1)# 得到全部的距离
            __ = np.argsort(_)
            for h in range(i, len(_)):
                if _[__[h]] != _[__[h-1]]:
                    break
            _ = [train_y[hh] for hh in __[:h]]
            if train_y[t]  != stats.mode(_,keepdims=False)[0][0]:
                ans += 1
        ta += ans
    Error[0].append(ta/k)
    Error[1].append(te/k)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(kk,Error[0],color='r',marker='o',label='train')
plt.plot(kk,Error[1],color='b',marker='x',label='test')
plt.legend()
plt.show()
        

# 2-15
# 马修斯相关系数计算 k近邻
# 1姿势正确，2坐姿偏右，3坐姿偏左，4坐姿前倾
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(100)
rng.shuffle(data)
data=data.astype(np.float64)
# 输入特征维度
d = data.shape[1] - 1
# 数据最大最小归一化处理
maxs = np.amax(data[:,0:d],0)
mins = np.amin(data[:,0:d],0)
data[:,0:d] = (data[:,0:d] - mins) / (maxs - mins)
# 样本长度
lens = data.shape[0]
# 设置k交叉验证中 k的值
k = 4
# 测试集长度
test_m = lens // k
# k近邻分类 中的k值
kk = [i for i in range(1,21)]
Error = [[],[],[],[]]
# 求宏平均F1分数
for i in kk:
    ta,te,tta,tte = 0.,0.,0.,0.
    for j in range(k):
        tag_= []
        teg_= []
        # 区分训练集和测试集
        start = j*test_m
        ends = (j+1)*test_m if (j != k-1) else lens
        if j == 0:
            train_x,train_y = data[ends:,0:d],data[ends:,d:]
        elif j == k -1:
            train_x,train_y = data[0:start,0:d],data[0:start,d:]
        else:
            train_x,train_y=np.concatenate((data[0:start,0:d],data[ends:,0:d]),0),np.concatenate((data[0:start,d:],data[ends:,d:]),0)
        test_x,test_y = data[start:ends,0:d],data[start:ends,d:]
        # 计算距离
        for t in range(len(test_x)):
            _ = np.sum((train_x-test_x[t])*(train_x-test_x[t]),1)# 得到全部的距离
            __ = np.argsort(_) # 排序
            for h in range(i, len(_)):
                if _[__[h]] != _[__[h-1]]:
                    break
            _ = [train_y[hh] for hh in __[:h]]
            teg_.append(int(stats.mode(_,keepdims=False)[0][0]))
         # 计算距离
        teg_ = np.array(teg_).reshape(1,-1)
        for t in range(len(train_x)):
            _ = np.sum((train_x-train_x[t])*(train_x-train_x[t]),1)# 得到全部的距离
            __ = np.argsort(_)
            for h in range(i, len(_)):
                if _[__[h]] != _[__[h-1]]:
                    break
            _ = [train_y[hh] for hh in __[:h]]
            tag_.append(int(stats.mode(_,keepdims=False)[0][0]))
        # 计算F1分数
        # 计算方法就是 测试集和训练集分别一个宏均F1分数，
        # 其次采用了k交叉验证，最终的F1分数是这k次计算结果的宏均F1的平均值
        tag_ = np.array(tag_).reshape(1,-1)
        def G(a,b):
            allp = np.sum(b)
            c = a*b
            TP = np.sum(c)
            FP = np.sum(a*(1-c))
            if FP + TP == 0:return 0
            R = TP/allp
            P = TP/(FP+TP)
            if not P:return 0
            return 2/(1/R + 1/P)
        def getF1(li1,li2):
            a,b,c,d = li1==4,li1==3,li1==2,li1==1
            a1,b1,c1,d1 =  li2==4.,li2==3.,li2==2.,li2==1.
            return (G(a,a1)+G(b,b1)+G(c,c1)+G(d,d1))/4
        te += getF1(teg_,test_y.transpose())
        ta += getF1(tag_,train_y.transpose())
        # 计算马修斯相关系数
        def getMCC(li1,li2):
            a,b,c,d = li1==4,li1==3,li1==2,li1==1
            a1,b1,c1,d1 =  li2==4.,li2==3.,li2==2.,li2==1.
            A = len(li1[0])
            S = np.sum(a*a1)+np.sum(b*b1)+np.sum(c*c1)+np.sum(d*d1)
            h = np.array([np.sum(a) , np.sum(b) , np.sum(c) , np.sum(d)])
            l = np.array([np.sum(a1) , np.sum(b1),np.sum(c1) , np.sum(d1)])
            _ = A*S - np.sum(h*l)
            __ = ((A*A - np.sum(h*h))*(A*A-np.sum(l*l)))**0.5
            return  _/__
        tte += getMCC(teg_,test_y.transpose())
        tta += getMCC(tag_,train_y.transpose())
            
    Error[0].append(ta/k)
    Error[1].append(te/k)
    Error[2].append(tta/k)
    Error[3].append(tte/k)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].plot(kk,Error[0],color='r',linestyle='dashed',label='train',marker='x')
axes[0].plot(kk,Error[1],color='b',linestyle='dashed',label='test',marker='o')
axes[0].legend()
axes[0].set_title('宏平均F1')
axes[1].plot(kk,Error[2],color='r',linestyle='dashed',label='train',marker='x')
axes[1].plot(kk,Error[3],color='b',linestyle='dashed',label='test',marker='o')
axes[1].legend()
axes[1].set_title('MCC')
plt.tight_layout()
plt.show()

# 高斯朴素贝叶斯分类器 2-16
# 1姿势正确，2坐姿偏右，3坐姿偏左，4坐姿前倾
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
data=data.astype(np.float64)
# 输入特征维度
d = data.shape[1] - 1
# 样本长度
lens = data.shape[0]
# 设置k交叉验证中 k的值
k = 4
# 测试集长度
test_m = lens // k
# k近邻分类 中的k值
kk = [i for i in range(1,21)]
Error = [[],[],[],[]]
# 求宏平均F1分数
for i in kk:
    ta,te,tta,tte = 0.,0.,0.,0.
    for j in range(k):
        tag_= []
        teg_= []
        # 区分训练集和测试集
        start = j*test_m
        ends = (j+1)*test_m if (j != k-1) else lens
        if j == 0:
            train_x,train_y = data[ends:,0:d],data[ends:,d:]
        elif j == k -1:
            train_x,train_y = data[0:start,0:d],data[0:start,d:]
        else:
            train_x,train_y=np.concatenate((data[0:start,0:d],data[ends:,0:d]),0),np.concatenate((data[0:start,d:],data[ends:,d:]),0)
        test_x,test_y = data[start:ends,0:d],data[start:ends,d:]
        # 高斯朴素贝叶斯
        # 计算ujk 和 pck
        def getUjkAndPck(lia,lib):
            ujk = np.array([[0. for _ in range(4)] for __ in range(d)]) # d *4 的矩阵，输入特征维度*类别总数
            times = [0 for _  in range (4)]
            for tt in range(len(lib)):
                kk = int(lib[tt])-1 # 得到的是 类别
                ujk[:,kk] += lia[tt]  #  注意横纵坐标的含义
                times[kk] += 1
            for _ in range(d):
                ujk[_] /= times 
            return ujk,np.array(times)/len(lia)
        # 方差的无偏估计量
        def getOjk2(lia,lib,ujk):
            Ojk2 = np.array([[0. for _ in range(4)] for __ in range(d)])
            times  = [0 for i in range(4)]
            for _ in range(len(lib)):
                kk = int(lib[_])-1
                Ojk2[:,kk] += (lia[_] - ujk[:,kk])**2 # 注意横纵坐标的含义
                times[kk] += 1
            times = np.array(times)-1
            for _ in range(d):
                Ojk2[_] /= times
            return Ojk2**0.5
        ujk,pck = getUjkAndPck(train_x,train_y.transpose()[0])
        Ojk2 = getOjk2(train_x,train_y.transpose()[0],ujk)
        # 测试集
        for _ in test_x:
            __ = (ujk.transpose() - _)/Ojk2.transpose()
            __ = __**2
            __ = np.log(pck)-0.5*np.sum(__,1) -np.sum(np.log(Ojk2).transpose(),1)
            teg_.append(np.argmax(__)+1)
        teg_ = np.array(teg_).reshape(1,-1)
        # 训练集
        for _ in train_x:
            __ = (ujk.transpose() - _)/Ojk2.transpose()
            __ = __**2
            __ = np.log(pck)-0.5*np.sum(__,1) -np.sum(np.log(Ojk2).transpose(),1)
            tag_.append(np.argmax(__)+1)
        tag_ = np.array(tag_).reshape(1,-1)
                            
                        

        
        # 计算F1分数
        # 计算方法就是 测试集和训练集分别一个宏均F1分数，
        # 其次采用了k交叉验证，最终的F1分数是这k次计算结果的宏均F1的平均值
        
        def G(a,b):
            allp = np.sum(b)
            c = a*b
            TP = np.sum(c)
            FP = np.sum(a*(1-c))
            if FP + TP == 0:return 0
            R = TP/allp
            P = TP/(FP+TP)
            if not P:return 0
            return 2/(1/R + 1/P)
        def getF1(li1,li2):
            a,b,c,d = li1==4,li1==3,li1==2,li1==1
            a1,b1,c1,d1 =  li2==4.,li2==3.,li2==2.,li2==1.
            return (G(a,a1)+G(b,b1)+G(c,c1)+G(d,d1))/4
        te += getF1(teg_,test_y.transpose())
        ta += getF1(tag_,train_y.transpose())
        # 计算马修斯相关系数
        def getMCC(li1,li2):
            a,b,c,d = li1==4,li1==3,li1==2,li1==1
            a1,b1,c1,d1 =  li2==4.,li2==3.,li2==2.,li2==1.
            A = len(li1[0])
            S = np.sum(a*a1)+np.sum(b*b1)+np.sum(c*c1)+np.sum(d*d1)
            h = np.array([np.sum(a) , np.sum(b) , np.sum(c) , np.sum(d)])
            l = np.array([np.sum(a1) , np.sum(b1),np.sum(c1) , np.sum(d1)])
            _ = A*S - np.sum(h*l)
            __ = ((A*A - np.sum(h*h))*(A*A-np.sum(l*l)))**0.5
            return  _/__
        tte += getMCC(teg_,test_y.transpose())
        tta += getMCC(tag_,train_y.transpose())
            
    Error[0].append(ta/k)
    Error[1].append(te/k)
    Error[2].append(tta/k)
    Error[3].append(tte/k)
# 绘图部分
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig, axes = plt.subplots(nrows=1, ncols=2)
axes[0].plot(kk,Error[0],color='r',linestyle='dashed',label='train',marker='x')
axes[0].plot(kk,Error[1],color='b',linestyle='dashed',label='test',marker='o')
axes[0].legend()
axes[0].set_title('宏平均F1')
axes[1].plot(kk,Error[2],color='r',linestyle='dashed',label='train',marker='x')
axes[1].plot(kk,Error[3],color='b',linestyle='dashed',label='test',marker='o')
axes[1].legend()
axes[1].set_title('MCC')
plt.tight_layout()
plt.show()

# 多分类逻辑回归 2-17
# 1姿势正确，2坐姿偏右，3坐姿偏左，4坐姿前倾
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
data=data.astype(np.float64)
# 输入特征维度
d = data.shape[1] - 1
# 样本长度
lens = data.shape[0]
# 设置训练次数
epochs = 5000
# 设置学习率
xuexi = 0.1
# 标准化处理
mean  = np.mean(data[:,:d],0)
stds = np.std(data[:,:d],0,ddof=1)
data[:,:d] = (data[:,:d]-mean)/stds
# 多分类逻辑回归
# 初始化 w，b
w = np.array([[rd.uniform(0,1) for __ in range(d)] for _ in range(4)]) # c * d
b = np.array([[rd.uniform(0,1) ] for _ in range(4)]) # c*1
# y-> one-hot
datay = np.array([[i==1.,i==2.,i==3.,i==4.] for i in data[:,d]])
# 划分数据集和测试集
train_m = int(lens*0.8)
test_m = lens - train_m
train_x,train_y,test_x,test_y = data[:train_m,:d],datay[:train_m],data[train_m:,:d],datay[train_m:]#  x:m*d,y:m*c
Errors = [[],[],[],[]]
for _ in range(epochs):
    # 更新w,b
    # 第一步计算 Z
    Z = np.dot(w,train_x.transpose()) + np.dot(b,np.ones(train_m).reshape(1,-1))
    # 计算 Y^
    _ = np.random.rand(4,4)>0 # c*c矩阵
    Y_ = np.exp(Z)/np.dot(_,np.exp(Z)) # c*m
    # 计算 E
    E = Y_ - train_y.transpose() # c*m
    # 计算多类别逻辑回归交叉熵
    TaJwb = np.trace(np.dot(train_y,np.log(Y_)))/-train_m
    Errors[2].append(TaJwb)
    # 统计训练集出错
    _ = np.argmax(Y_,0) + 1
    _ = _.astype(np.float64)
    _ -= data[:train_m,d]
    taer = np.sum(_ > 0)
    taer += np.sum(_ < 0)
    Errors[0].append(taer)
    # 统计测试集出错
    # 第一步计算 Z
    Z = np.dot(w,test_x.transpose()) + np.dot(b,np.ones(test_m).reshape(1,-1))
    # 计算 Y^
    _ = np.random.rand(4,4)>0 # c*c矩阵
    Y_ = np.exp(Z)/np.dot(_,np.exp(Z)) # c*m
    _ = np.argmax(Y_,0) + 1
    _ = _.astype(np.float64)
    _ -= data[train_m:,d]
    teer = np.sum(_ > 0)
    teer += np.sum(_ < 0)
    Errors[1].append(teer)
    # 更新w,b
    b -= np.dot(E,np.ones(train_m).reshape(-1,1))/train_m
    w -= np.dot(E,train_x)/train_m
# 绘图部分
print(Errors[0][-1],Errors[1][-1],Errors[2][-1])
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
fig, axes = plt.subplots(nrows=1, ncols=2)
kk = [i for i in range(epochs)]
axes[0].plot(kk,Errors[0],color='r',linestyle='dashed',label='train',marker='x')
axes[0].plot(kk,Errors[1],color='b',linestyle='dashed',label='test',marker='x')
axes[0].legend()
axes[0].set_title('trainErrors')
axes[1].plot(kk,Errors[2],color='r',linestyle='dashed',label='train',marker='x')
axes[1].legend()
axes[1].set_title('交叉熵')
plt.tight_layout()
plt.show()
    

# 二分类逻辑回归对其进行预测
import numpy as np
import random as rd
x_train = np.array([0, 5, 10, 25, 30, 35, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73]).reshape((1, -1))
y_train = np.array([0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
m_train = x_train.size # number of training examples
# 第一步随机排序  （这里感觉不用）
epoch = 30000 # 训练次数
xuexi = 0.0001 # 学习率
# 设置权重和偏差
w = 0.
b = 0.
for _ in range(epoch):
    # 第一步计算e
    Y_ = 1/(1+np.exp(-(w*x_train + b)))
    e = Y_ - y_train
    # 更新 w,b
    b -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_train
    w -= xuexi*np.dot(x_train,e.transpose())/m_train
# 绘图部分
Y =  1/(1+np.exp(-(w*x_train + b)))
print(Y)
# lines = 60*w + b
Y_= Y >= 0.5
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号

kk = [i for i in range(epochs)]
plt.plot(x_train[0],Y[0],color='k',linestyle='dashed',label='train')
plt.plot(x_train[0],Y_[0],color='r',linestyle='dashed',label='predict')
plt.scatter(x_train,y_train[0],color='b',label='原本',marker='x')
plt.legend()
plt.title('变化')
plt.tight_layout()
plt.show()

# 二分类逻辑回归对其进行预测
# 强化
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
x_train = np.array([0, 5, 10, 25, 30, 35, 50, 51, 52, 53, 54, 55, 56, 57, 58, 59, 61, 62, 63, 64, 65, 66, 67, 68, 69, 70, 71, 72, 73]).reshape((1, -1))
y_train = np.array([0, 0, 0, 1, 1, 1, 0, 0, 0, 0, 0, 0, 0, 0, 0, 0, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1, 1]).reshape((1, -1))
m_train = x_train.size # number of training examples
# 第一步随机排序  （这里感觉不用）
epoch = 30000 # 训练次数
xuexi = 0.001 # 学习率
# 设置权重和偏差
# 标准化
x_train=x_train.astype(np.float64)
mean = np.mean(x_train,1)
stds = np.std(x_train,1,ddof=1)
x_train = (x_train - mean)/stds
w0,w1,w2,w3 = 0.,0.,0.,0.
b0,b1,b2,b3 = 0.,0.,0.,0.
for _ in range(epoch):
    # 第一步计算e0
    Y_ = 1/(1+np.exp(-(w0*x_train + b0)))
    e = Y_ - y_train
    # 更新 w0,b0
    b0 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_train
    w0 -= xuexi*np.dot(x_train,e.transpose())/m_train
    # 第一步计算e1
    Y_ = 1/(1+np.exp(-(w1*x_train + b1)+17.5))
    e = Y_ - y_train
    # 更新 w,b
    b1 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_train
    w1 -= xuexi*np.dot(x_train,e.transpose())/m_train
    # 第一步计算e2
    Y_ = 1/(1+np.exp(-(w2*x_train + b2)  - 42.5))
    e = Y_ - y_train
    # 更新 w,b
    b2 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_train
    w2 -= xuexi*np.dot(x_train,e.transpose())/m_train
    # 第一步计算e3
    Y_ = 1/(1+np.exp(-(w3*x_train + b3) + 60))
    e = Y_ - y_train
    # 更新 w,b
    b3 -= xuexi*np.dot(e,np.ones(m_train).transpose())/m_train
    w3 -= xuexi*np.dot(x_train,e.transpose())/m_train
# 绘图部分
Y0 = 1/(1+np.exp(-(w0*x_train + b0)))
Y1 = 1/(1+np.exp(-(w1*x_train + b1)+17.5))
Y2 = 1/(1+np.exp(-(w2*x_train + b2)-42.5))
Y3 = 1/(1+np.exp(-(w3*x_train + b3)+60))
Y_ = [-1 for i in range(m_train)]
Yx = Y1+Y2+Y3 -1 
# lines = 60*w + b
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(x_train[0],Y0[0],color='k',linestyle='dashed',label='原本的',linewidth=3)
plt.plot(x_train[0],Y1[0],color='#ec2d7a',linestyle='dashdot',label='17.5',linewidth=3)
plt.plot(x_train[0],Y2[0],color='g',linestyle='solid',label='-42.5',linewidth=3)
plt.plot(x_train[0],Y3[0],color='darkviolet',linestyle=(2,(1,2,3,4,2,2)),label='+60',linewidth=3)
plt.plot(x_train[0],Y_,color='r',linestyle='solid',label='-1',linewidth=3)
plt.plot(x_train[0],Yx[0],color='springgreen',linestyle='dotted',label='混合',linewidth=3)
plt.scatter(x_train,y_train[0],color='b',label='原本',marker='x')
plt.legend()
plt.title('变化')
plt.tight_layout()
plt.show()

# 2-18
# 实现二分类神经网络
# 导入酒驾数据
# d = 5
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
# load dataset
df = pandas.read_csv('alcohol_dataset.csv')
data = np.array(df)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
# 输入特征维度
d = data.shape[1] -1
# 训练次数
epoch = 300000
# 学习率
XX = 0.00001
# 最大最小归一化
maxs = np.max(data[:,:d],0)
mins = np.min(data[:,:d],0)

data[:,:d] = (data[:,:d]-mins)/(maxs-mins)
# mean  = np.mean(data[:,:d],0)
# stds = np.std(data[:,:d],0,ddof=1)
# data[:,:d] = (data[:,:d]-mean)/stds
# 训练集测试集划分
train_m = int(data.shape[0]*0.8)
test_m = data.shape[0] - train_m
train_x,train_y,test_x,test_y = data[:train_m,:d],data[:train_m,d:],data[train_m:,:d],data[train_m:,d:]
# train_x m*d, train_y  m*1, test_x m*d
# 设置隐含层节点数
n = 2
# 初始化初始权重w1  d*n和偏差 b1 n*1
w1 = np.array([[rd.uniform(0,1) for _ in range(n)] for __ in range(d)])
b1 = np.array([rd.uniform(0,1) for i in range(n)]).reshape(-1,1)
# 初始化初始权重 w2 n*1 和偏差 b2 是常数
w2 = np.array([rd.uniform(0,1) for _ in range(n)]).reshape(-1,1)
b2 = rd.uniform(0,1)
# 存储错误
Errors = [[],[]]
# 激活函数
def ReLU(x):
    global n
    return np.maximum(0, x).reshape(n,-1)
# 训练
for _ in range(epoch):
    # 求训练集预测值部分
    # 第一步计算 Z1 n*m
    Z1 = np.dot(w1.transpose(),train_x.transpose())  + np.dot(b1,np.ones(train_m).reshape(1,-1))
    # 激活函数是ReLU 计算A1 n*m
    A1 = ReLU(Z1)
    # 计算Z2 1*m
    Z2 = np.dot(w2.transpose(),A1) + b2
    # 输出层使用的是sigmoid 激活函数 ,预测值为 predict_y
    predict_y = 1/(1+np.exp(-Z2))
    # 更新权重部分
    # e 计算 m*1
    e = predict_y.transpose() - train_y
    predict_y ,train_y= predict_y.transpose()>=0.5,train_y >= 0.5
    Errors[0].append(np.sum(predict_y^train_y))
    # 更新 b1
    b1 -= XX*w2*np.dot(A1,e)/train_m
    # 更新 w1
    w1 -= XX*np.dot(train_x.transpose(),((np.dot(w2,e.transpose()))*A1).transpose())
    # 更新b2
    b2 -= XX*np.dot(np.ones(train_m).reshape(1,-1),e)/train_m
    # 更新 w2
    w2 -= XX*np.dot(A1,e)/train_m
     # 求测试集预测值部分
    # 第一步计算 Z1 n*m
    Z1 = np.dot(w1.transpose(),test_x.transpose())  + np.dot(b1,np.ones(test_m).reshape(1,-1))
    # 激活函数是ReLU 计算A1 n*m
    A1 = ReLU(Z1)
    # 计算Z2 1*m
    Z2 = np.dot(w2.transpose(),A1) + b2
    # 输出层使用的是sigmoid 激活函数 ,预测值为 predict_y
    predict_y = 1/(1+np.exp(-Z2))
    # 更新权重部分 
    predict_y ,test_y= predict_y.transpose()>=0.5,test_y >= 0.5
    Errors[1].append(np.sum(predict_y^test_y))
    
# 绘图部分
print(min(Errors[0]),min(Errors[1]))
X = [i+1 for i in range(epoch)]
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(X,Errors[1],color='k',linestyle='dashed',label='测试集错误',linewidth=3)
plt.plot(X,Errors[0],color='#ec2d7a',linestyle='dashdot',label='训练集错误',linewidth=3)
plt.legend()
plt.title('二分类神经网络')
plt.tight_layout()
plt.show()

# 2-19
# 实现多分类神经网络
# 1姿势正确，2坐姿偏右，3坐姿偏左，4坐姿前倾
# d = 4
import matplotlib.pyplot as plt
import pandas
import numpy as np
from scipy import stats
import random as rd
# load dataset
df = pandas.read_csv('wheelchair_dataset.csv')
data = np.array(df)
data=data.astype(np.float64)
# 随机排序
rng = np.random.default_rng(1)
rng.shuffle(data)
# 输入特征维度
d = data.shape[1] -1
# 训练次数
epoch = 3000
# 学习率
XX = 0.1
# 最大最小归一化
# maxs = np.max(data[:,:d],0)
# mins = np.min(data[:,:d],0)
# data[:,:d] = (data[:,:d]-mins)/(maxs-mins)
mean  = np.mean(data[:,:d],0)
stds = np.std(data[:,:d],0,ddof=1)
data[:,:d] = (data[:,:d]-mean)/stds
# 训练集测试集划分
train_m = int(data.shape[0]*0.8)
test_m = data.shape[0] - train_m
train_x,train_y,test_x,test_y = data[:train_m,:d],data[:train_m,d:],data[train_m:,:d],data[train_m:,d:]
train_y,test_y = train_y.transpose(),test_y.transpose()
train_y,test_y = np.array([train_y[0]==1.,train_y[0]==2.,train_y[0]==3.,train_y[0]==4.]),np.array([test_y[0]==1.,test_y[0]==2.,test_y[0]==3.,test_y[0]==4.])
# train_x m*d, train_y  c*m, test_x m*d
# 设置隐含层节点数
n = 3
# 初始化初始权重w1  d*n和偏差 b1 n*1
w1 = np.array([[rd.uniform(0,1) for _ in range(n)] for __ in range(d)])
b1 = np.array([rd.uniform(0,1) for i in range(n)]).reshape(-1,1)
# 初始化初始权重 w2 n*c 和偏差 b2 c*1
w2 = np.array([[rd.uniform(0,1) for _ in range(4)] for __ in range(n)])
b2 = np.array([rd.uniform(0,1) for i in range(4)]).reshape(-1,1)
# 存储错误
Errors = [[],[]]
# 激活函数
def ReLU(x):
    global n
    return np.maximum(0, x).reshape(n,-1)
# 训练
for _ in range(epoch):
    # 求训练集预测值部分
    # 第一步计算 Z1 n*m
    Z1 = np.dot(w1.transpose(),train_x.transpose())  + np.dot(b1,np.ones(train_m).reshape(1,-1))
    # 激活函数是ReLU 计算A1 n*m
    A1 = ReLU(Z1)
    # 计算Z2 c*m
    Z2 = np.dot(w2.transpose(),A1) + np.dot(b2,np.ones(train_m).reshape(1,-1))
    # 输出层使用的是sigmoid 激活函数 ,预测值为 predict_y
    predict_y = np.exp(Z2)/np.dot(np.ones(4*4).reshape(4,4),np.exp(Z2))
    # 更新权重部分
    # E 计算 c*m
    E = predict_y - train_y
    # 统计错误
    e = np.argmax(predict_y,0)-np.argmax(train_y,0)
    Errors[0].append(np.sum(e*e))
    # 更新 b1
#     print('w2',w2.shape,'E',E.shape,'A1',A1.shape)
    b1 -= XX*np.dot(np.dot(w2,E)*A1,np.ones(train_m).reshape(-1,1))/train_m
    # 更新 w1
    w1 -= XX*np.dot(train_x.transpose(),(np.dot(w2,E)*A1).transpose())/train_m
    # 更新b2
    b2 -= XX*np.dot(E,np.ones(train_m).reshape(-1,1))/train_m
    # 更新 w2
    w2 -= XX*np.dot(A1,E.transpose())/train_m
     # 求测试集预测值部分
    Z1 = np.dot(w1.transpose(),test_x.transpose())  + np.dot(b1,np.ones(test_m).reshape(1,-1))
    # 激活函数是ReLU 计算A1 n*m
    A1 = ReLU(Z1)
    # 计算Z2 c*m
    Z2 = np.dot(w2.transpose(),A1) + np.dot(b2,np.ones(test_m).reshape(1,-1))
    # 输出层使用的是sigmoid 激活函数 ,预测值为 predict_y
    predict_y = np.exp(Z2)/np.dot(np.ones(4*4).reshape(4,4),Z2)
    # 更新权重部分
    # 统计错误
    e = np.argmax(predict_y,0)-np.argmax(test_y,0)
    Errors[1].append(np.sum(e*e))
    
# 绘图部分
print(min(Errors[0]),min(Errors[1]))
X = [i+1 for i in range(epoch)]
plt.rcParams['font.sans-serif']=['SimHei'] #用来正常显示中文标签
plt.rcParams['axes.unicode_minus']=False #用来正常显示负号
plt.plot(X,Errors[1],color='k',linestyle='dashed',label='测试集错误',linewidth=3)
plt.plot(X,Errors[0],color='#ec2d7a',linestyle='dashdot',label='训练集错误',linewidth=3)
plt.legend()
plt.title('多分类神经网络')
plt.tight_layout()
plt.show()

资源地址

gitee地址