上采样方法

目录

上采样(Upsampling) 方法

去池化

最近邻方法

钉床方法

最大去池化

双线性插值

反卷积

膨胀卷积

---

上采样(Upsampling) 方法

上采样：是指将低分辨率的图像或特征图放大到原始分辨率的过程。在计算机视觉中，上采样通常用于图像分割、目标检测和图像生成等任务中，可以帮助提高模型的准确性和性能。

常见的上采样方法包括双线性插值、最近邻插值、反卷积等。其中，双线性插值和最近邻插值是最简单和最常用的上采样方法，反卷积则是一种专门用于卷积神经网络中的上采样方法。

下采样：是指将高分辨率的图像或特征图缩小到较低分辨率的过程。在计算机视觉中，下采样通常用于图像分类、目标检测和图像分割等任务中，可以帮助减少计算量和内存消耗，加快模型的训练和推理速度。

作用：一是减少计算量，防止过拟合

二是增大感受野，使得后面的卷积核能够学到更加全局的信息。

常见的下采样方法包括平均池化、最大池化和卷积操作等。其中，池化操作是一种常用的下采样方法，可以通过对图像或特征图进行平均或最大值的池化操作来实现下采样。卷积操作也可以实现下采样，常用的方法包括步长卷积和空洞卷积。

去池化

定义：将经过池化（下采样）操作的特征图恢复到原始尺寸的过程。与传统的插值方法不同，去池化是一种可学习的上采样方法，可以通过反向传播算法自动学习和优化池化操作的位置和值，从而获得更加精确的上采样结果。

去池化的原理是将池化操作进行反向计算。具体来说，去池化会在经过池化操作的特征图中，根据池化操作的位置和值进行填充，并将原始像素的值复制到对应位置，从而实现上采样的效果。去池化的过程通常是通过记录池化操作的位置和值，然后在反向传播时将原始像素的值复制到对应位置实现的。

在实际应用中，去池化通常用于图像分割、目标检测和图像生成等任务中，可以帮助提高模型的准确性和性能。去池化的优点是可以自动学习和优化池化操作的位置和值，从而获得更加精确的上采样结果，同时也可以避免插值方法带来的模糊和失真等问题。不过，去池化的计算量也较大，需要消耗大量的计算资源，因此在实际应用中需要进行合理的调整和优化。

最近邻方法

定义：最近邻方法（nearest neighbor method）是一种常用的插值方法，用于将低分辨率的图像或特征图放大到高分辨率的过程。该方法的原理是对于每个需要放大的像素，选择最近的像素作为其放大后的值。

具体来说，最近邻方法会将低分辨率的图像或特征图中的每个像素放大到一定大小，并在放大后的像素矩阵中选择最近的像素作为其放大后的值。例如，将一个2×2的低分辨率像素矩阵放大到4×4的高分辨率像素矩阵时，最近邻方法会将每个像素放大为2×2的大小，并在放大后的像素矩阵中选择最近的像素作为其放大后的值。

优点：最近邻方法具有简单、快速的优点，可以在不消耗太多计算资源的情况下实现图像或特征图的上采样。

缺点：最近邻方法存在着失真和锯齿等问题，因为它只考虑了离放大像素最近的像素的值，而没有考虑周围像素的信息。在一些对图像质量要求较高的任务中，如图像生成和图像超分辨率等任务，通常不推荐使用最近邻方法，而是使用更加精确的插值方法，如双线性插值、双三次插值等。

在PyTorch中，我们可以使用torch.cdist函数来计算两组样本之间的距离，并使用torch.topk函数找到距离最近的k个样本。具体实现如下

import torch

def knn_classifier(train_data, train_labels, test_data, k):
    """
    KNN分类器，使用最近邻方法进行分类

    参数：
    train_data: 训练数据，形状为(N, D)，其中N表示样本数，D表示特征维度
    train_labels: 训练数据的标签，形状为(N,)
    test_data: 测试数据，形状为(M, D)，其中M表示测试样本数，D表示特征维度
    k: 最近邻的个数

    返回值：
    test_labels: 测试数据的标签，形状为(M,)
    """
    # 计算测试样本和训练样本之间的距离
    dist = torch.cdist(test_data, train_data)

    # 找到距离最近的k个样本
    _, indices = torch.topk(dist,k=k, largest=False)

    # 根据距离最近的k个样本的标签，预测测试样本的标签
    train_labels = train_labels.unsqueeze(0).repeat(test_data.shape[0], 1)
    nearest_labels = train_labels.gather(1, indices)
    test_labels, _ = torch.mode(nearest_labels, dim=1)

    return test_labels

在这个函数中，我们首先使用torch.cdist函数计算测试数据和训练数据之间的距离。该函数接受两个张量作为输入，分别表示测试数据和训练数据，返回一个形状为(M, N)的距离矩阵，其中M表示测试样本数，N表示训练样本数。

接着，我们使用torch.topk函数找到距离最近的k个样本。该函数接受两个参数，第一个参数为待排序的张量，第二个参数为要找到的最大或最小的k个元素。我们在这里选择了最小的k个元素。

然后，我们根据距离最近的k个样本的标签，预测测试样本的标签。具体来说，我们使用train_labels.gather函数根据indices从训练标签中获取最近的k个标签，并将这些标签传递给nearest_labels张量。然后使用torch.mode函数取nearest_labels中的众数作为测试标签。

最后，我们将预测的测试标签作为输出结果返回。这个函数可以使用以下方式进行调用：

import torch

# 创建训练数据和标签
train_data = torch.randn(100, 10)
train_labels = torch.randint(0, 5, (100,))

# 创建测试数据
test_data = torch.randn(20, 10)

# 使用最近邻方法进行分类
test_labels = knn_classifier(train_data, train_labels, test_data, k=5)

# 打印测试标签
print(test_labels)

在这个例子中，我们使用了一个形状为(100, 10)的训练数据，100个样本，每个样本有10个特征。我们还使用了一个形状为(20, 10)的测试数据，20个样本，每个样本有10个特征。最后，我们将k设置为5，使用最近邻方法对测试数据进行分类，并打印输出的测试标签。

钉床方法

定义：钉床方法（bicubic convolution interpolation）是一种常用的插值方法，用于将低分辨率的图像或特征图放大到高分辨率的过程。与最近邻方法和双线性插值等方法相比，钉床方法可以获得更加精确的上采样结果，同时也具有计算速度较快的优点。

原理：是在低分辨率的图像或特征图周围取一定大小的像素块，并通过三次样条函数对像素块进行插值，从而获得放大后的像素值。具体来说，钉床方法会在低分辨率的图像或特征图周围取一个3×3的像素块，并使用三次样条函数对像素块中的像素进行插值，从而计算出放大后的像素值。

钉床方法相比于最近邻方法和双线性插值等方法，具有更加平滑和精细的上采样效果，可以有效地避免失真和锯齿等问题。

不过，钉床方法也存在着计算量较大的问题，在实际应用中需要进行合理的调整和优化。

需要注意的是，钉床方法的插值过程是基于像素块的，因此在实际应用中需要考虑像素块的大小和选择方法，以及三次样条函数的参数等问题，从而获得更加精确和有效的上采样结果。

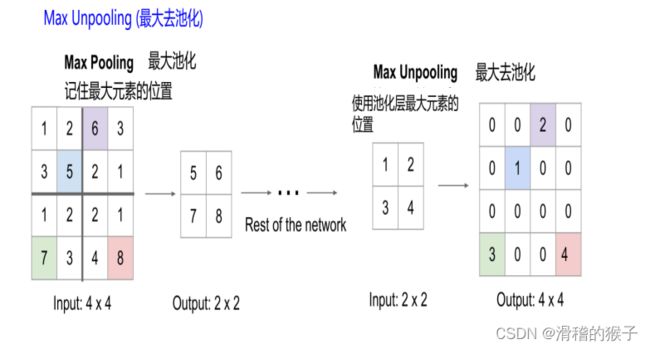
最大去池化

最大去池化（max pooling）是一种常用的下采样方法，用于将输入数据的空间尺寸减小，同时保留重要的特征信息。它通常用于卷积神经网络（CNN）中，以减少卷积层输出的参数数量，从而加速训练和提高模型的泛化能力。

最大池化的操作很简单，它将输入图像分成不重叠的矩形区域，对于每个区域，取其内部元素的最大值作为输出。最大池化通常可以通过设置步长和池化核的大小来控制输出的尺寸。

最大池化的优点在于它能够保留输入数据中的重要特征，因为最大池化操作只取每个区域内的最大值，而忽略其他元素。同时，最大池化还具有一定的平移不变性，也就是说，即使输入图像在一定程度上发生平移，最大池化操作仍然能够提取出相同的特征。

需要注意的是，最大池化可能会导致信息丢失，因为它舍弃了非最大值的信息。此外，过度使用最大池化也可能会导致输出图像的分辨率过低，从而影响模型的性能。因此，在实际应用中，需要根据具体问题进行选择和调整。

双线性插值

双线性插值（bilinear interpolation）是一种常用的图像处理技术，用于在已知离散数据点的情况下，计算在任意位置的插值值。它通常用于图像缩放、旋转等操作中，以提高图像的质量和精度。

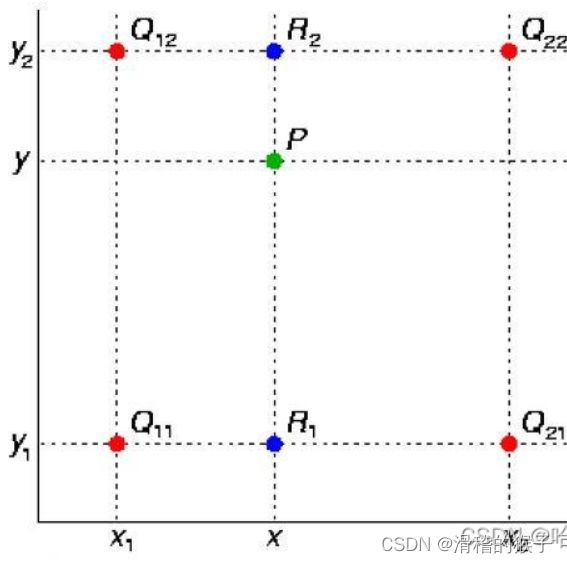
双线性插值的基本思想是，对于给定的插值位置，先在数据点坐标系中找到其所在的四个数据点，然后按照位置关系进行加权平均，得到插值结果。

双线性插值的优点在于它具有较高的计算效率和插值精度，同时可以避免出现锯齿状的插值结果。但需要注意的是，双线性插值仅适用于在较小范围内的插值问题，如果插值范围过大，可能会导致插值结果的误差较大。此外，双线性插值还需要保证数据点之间的间距足够小，以确保插值结果的精度。

应用领域：

图像缩放：在图像缩放过程中，双线性插值可以用于计算新图像中的每个像素值，以提高缩放后图像的质量和精度。

图像旋转：在图像旋转过程中，双线性插值可以用于计算旋转后图像中的每个像素值，以提高旋转后图像的质量和精度。

图像变形：在图像变形过程中，双线性插值可以用于计算变形后图像中的每个像素值，以提高变形后图像的质量和精度。

计算机图形学：在计算机图形学中，双线性插值可以用于计算多边形顶点的坐标值，以平滑多边形的边缘，提高图形的视觉效果。

数字信号处理：在数字信号处理中，双线性插值可以用于计算滤波器的输出值，以提高滤波器的精度和稳定性。

转置卷积可以将图扩大尺寸，细化粗特征图。但是存在一个棋盘效应问题。

棋盘效应： 转置卷积不均匀重叠导致的，使得图像变得有棋盘格一样的像素块

单线性插值

 给出两点，算出方程，然后求中间任一点y。公式如下

然后将对应的y值插入即可。

双线性插值

双线性插值可以看成是经过三次单线性插值

反卷积

反卷积是一种用于卷积神经网络中的上采样方法，可以将低分辨率的特征图放大到原始分辨率的过程。与传统的插值方法不同，反卷积是一种可学习的上采样方法，可以通过反向传播算法自动学习和优化卷积核参数，从而获得更加精确的上采样结果。

反卷积的原理是将卷积操作进行反向计算，即将卷积核进行旋转180度，并对特征图进行填充和卷积操作，从而实现上采样的效果。具体来说，反卷积会在低分辨率特征图的每个像素周围填充一定数量的零，并使用旋转后的卷积核对特征图进行卷积操作，从而生成高分辨率的特征图。

kernel核张量与输入的张量中，逐个元素相乘，放在对应的地方。就是说第一个元素是0，就是0乘上整个核张量，放在对应的位置。第二个元素是1则是乘上核张量放在对应滑动到下一个位置。以此类推。得到四个图，将四个图相加即可得出最终输出。此处的例子stride为1，所以滑动的步长是1。

总结出来的公式为：

Y [ i : i + h , j : j + w ] + = X [ i , j ] ∗ K Y[i:i+h, j:j + w] += X[i,j] * K

Y[i:i+h,j:j+w]+=X[i,j]∗K

其中Y的大小就是卷积的大小计算公式反过来：

卷积： out = (Input - kernel + 2*padding) / stride + 1

反卷积： out = (Input - 1) * stride + kernel - 2*padding

应用领域：在实际应用中，反卷积通常用于图像分割、目标检测和图像生成等任务中，可以帮助提高模型的准确性和性能。

优点：是可以自动学习和优化卷积核参数，从而获得更加精确的上采样结果，同时也可以避免插值方法带来的模糊和失真等问题。

缺点：反卷积的计算量较大，需要消耗大量的计算资源，因此在实际应用中需要进行合理的调整和优化。

膨胀卷积

膨胀卷积（dilated convolution）是一种卷积神经网络（CNN）中常用的卷积操作，也被称为空洞卷积（Atrous Convolution），可以用于提取输入数据中不同尺度的特征信息。与普通卷积不同的是，膨胀卷积在卷积核内部插入一定数量的空隙，从而扩大卷积核的感受野，使其能够捕捉更广阔区域内的特征。

具体来说，膨胀卷积的操作可以表示为：

$y_{i,j}=\sum_{k=1}^{K}\sum_{l=1}^{L}x_{i+rk,j+rl}h_{k,l}$

其中，x表示输入数据，h表示卷积核，y表示卷积结果，K和L分别表示卷积核的高度和宽度，r表示膨胀率（dilation rate），表示在卷积核内插入的空隙数量。

膨胀卷积有一个超参数：膨胀因子S，通过膨胀因子我们可以控制卷积核的膨胀程度，下图中的膨胀因子为2。膨胀因子是如何控制卷积核的膨胀程度

K c = S × ( K o − 1 ) + 1

参数含义：

K c :普通卷积核通过膨胀设计后的卷积核尺寸

K o :普通卷积核尺寸

例如下图中，普通卷积核尺寸3×3，S 为2，那么膨胀之后的卷积核尺寸为5×5。

膨 胀 卷 积 核 元 素 之 间 的 间 隔 = S − 1 ，图中S = 2 ，行列元素间隔各为1。

膨胀卷积的卷积核是在普通卷积核的基础上扩大了尺寸，但是真正参与运算的卷积核单元没有变化（图中只有蓝色方块才是参与运算的单元，无色小方块中的元素用0填充。左半部分的普通卷积核尺寸为３×3，右半部分卷积核尺寸为５×５，但右半部分深蓝色的参与运算的元素依然是９ [ 3 × 3 3×33×3 ] 个）

与普通卷积相比，膨胀卷积具有以下几个优点：

可以捕捉不同尺度的特征信息，因为膨胀卷积可以扩大卷积核的感受野，从而提高模型对不同尺度特征的识别能力。

可以减少参数数量和计算量，因为膨胀卷积不需要增加卷积核的大小，就可以增加感受野，从而提高模型的效率和泛化能力。

可以避免过拟合，因为膨胀卷积可以减少模型的参数数量和复杂度，从而降低过拟合的风险。

膨胀卷积在许多CNN中都得到了广泛的应用，如ResNet、DenseNet等。需要注意的是，膨胀率的选择需要根据具体问题进行调整，一般来说，较小的膨胀率可以捕捉更细节的特征，而较大的膨胀率可以捕捉更宽阔的特征。

膨胀卷积优缺点

优点：使得输出更为稠密，适应语义分割任务；

在不降低分辨率的情况下，增大感受野。

缺点：

1.gridding problem，如果我们叠加多个相同的膨胀卷积，会发现感受野中有很多像素没有利用上（感受野的方阵中只有蓝色和红色方块参与计算，白色方块使用零填充，相当于没有参与运算），出现大量空洞，如图所示。此时，会丢失数据之间的连续性及完整性，不利于学习。

2.长距离的信息有时是不相关的，膨胀卷积扩大了感受野，因此可以取得长距离信息（在图像中这是有利于大目标分析的），但是有些长距离信息和当前点是完全不相关的，会影响数据的一致性（对于小目标不太友好）。