sheng的学习笔记-【中英】【吴恩达课后测验】Course 1 - 神经网络和深度学习 - 第四周测验
课程1_第4周_测验题
目录:目录
第一题
1.在我们的前向传播和后向传播实现中使用的 “缓存” 是什么?
A. 【 】它用于在训练期间缓存成本函数的中间值。
B. 【 】我们用它将在正向传播过程中计算的变量传递到相应的反向传播步骤。它包含了反向传播计算导数的有用值。
C. 【 】它用于跟踪我们正在搜索的超参数,以加快计算速度。
D. 【 】我们用它将反向传播过程中计算的变量传递到相应的正向传播步骤。它包含用于计算正向传播的激活的有用值。
答案:
B.【 √ 】我们用它传递前向传播中计算的变量到相应的反向传播步骤,它包含用于计算导数的反向传播的有用值。
note:“cache” 记录来自正向传播单元的值并将其发送到反向传播单元,因为需要链式计算导数。
第二题
2.以下哪些是“超参数”?(选出所有正确项)
A. 【 】隐藏层规模 n [ l ] n^{[l]} n[l]
B. 【 】神经网络的层数 L L L
C. 【 】激活向量 a [ l ] a^{[l]} a[l]
D. 【 】权重矩阵 W [ l ] W^{[l]} W[l]
E. 【 】学习率 α \alpha α
F. 【 】迭代次数
G. 【 】偏置向量 b [ l ] b^{[l]} b[l]
答案:
A.【 √ 】隐藏层规模 n [ l ] n^{[l]} n[l]
B.【 √ 】神经网络的层数 L L L
E.【 √ 】学习率 α \alpha α
F.【 √ 】迭代次数
第三题
3.下列哪个说法是正确的?
A. 【 】神经网络的更深层通常比前面的层计算更复杂的特征。
B. 【 】神经网络的前面的层通常比更深层计算更复杂的特性。
答案:
A.【 √ 】神经网络的更深层通常比前面的层计算更复杂的输入特征。
第四题
4.向量化允许您在L层神经网络中计算前向传播时,不需要在层l = 1, 2, …, L间显式的使用for循环(或任何其他显式迭代循环),正确吗?
A. 【 】正确
B. 【 】错误
答案:
B.【 √ 】错误
note:在层间计算中,我们不能避免for循环迭代。
第五题
5.假设我们将 n [ l ] n ^ {[l]} n[l]的值存储在名为layers的数组中,如下所示:layer_dims = [n_x, 4, 3, 2, 1]。 因此,第1层有4个隐藏单元,第2层有3个隐藏单元,依此类推。 您可以使用哪个for循环初始化模型参数?
for(i in range(1, len(layer_dims/2))):
parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i-1]) * 0.01
parameter[‘b’ + str(i)] = np.random.randn(layers[i], 1) * 0.01
for(i in range(1, len(layer_dims/2))):
parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i-1]) * 0.01
parameter[‘b’ + str(i)] = np.random.randn(layers[i-1], 1) * 0.01
for(i in range(1, len(layer_dims))):
parameter[‘W’ + str(i)] = np.random.randn(layers[i-1], layers[i]) * 0.01
parameter[‘b’ + str(i)] = np.random.randn(layers[i], 1) * 0.01
for(i in range(1, len(layer_dims))):
parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i-1]) * 0.01
parameter[‘b’ + str(i)] = np.random.randn(layers[i], 1) * 0.01
答案:
D.【 √ 】
for(i in range(1, len(layer_dims))):
parameter[‘W’ + str(i)] = np.random.randn(layers[i], layers[i-1]) * 0.01
parameter[‘b’ + str(i)] = np.random.randn(layers[i], 1) * 0.01
Note:矩阵运算,W矩阵与X特征向量相乘,W矩阵的列数与X特征向量的个数相等。
第六题
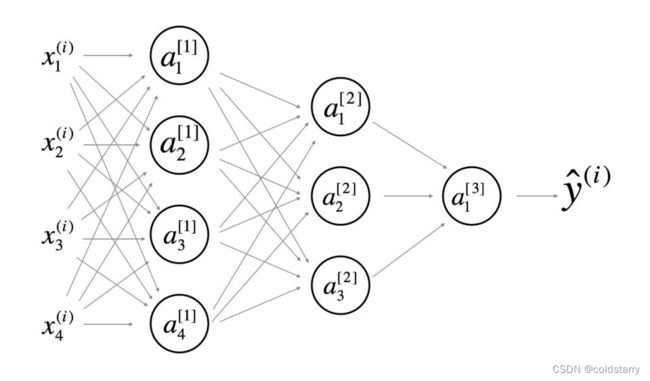
A. 【 】L层数是4,隐藏层数是3
B. 【 】L层数是3,隐藏层数是3
C. 【 】L层数是4,隐藏层数是4
D. 【 】L层数是5,隐藏层数是4
答案:
A.【 √ 】层数L为4,隐藏层数为3。
note:正如图中所看到的那样,层数被计为隐藏层数+1。输入层和输出层不计为隐藏层。
第七题
7.在前向传播期间,在层 l l l的前向传播函数中,您需要知道层 l l l中的激活函数(Sigmoid,tanh,ReLU等)是什么。在反向传播期间,相应的反向传播函数也需要知道第 l l l层的激活函数是什么,因为梯度是根据它来计算的。
A. 【 】对
B. 【 】不对
答案:
A.【 √ 】对
note:在反向传播期间,您需要知道正向传播中使用哪种激活函数才能计算正确的导数。
第八题
8.有一些函数具有以下特性:
(i) 当使用浅网络计算时,需要一个大网络(我们通过网络中的逻辑门数量来度量大小)。
(ii) 但是当使用深网络来计算时,我们只需要一个指数级小的网络。
A. 【 】对
B. 【 】不对
答案:
A.【 √ 】对
第九题
A. 【 】 W [ 1 ] W^{[1]} W[1]的形状是 (4, 4)
B. 【 】 b [ 1 ] b^{[1]} b[1]的形状是 (4, 1)
C. 【 】 W [ 2 ] W^{[2]} W[2]的形状是 (3, 4)
D. 【 】 b [ 2 ] b^{[2]} b[2]的形状是 (3, 1)
E. 【 】 b [ 3 ] b^{[3]} b[3]的形状是 (1, 1)
F. 【 】 W [ 3 ] W^{[3]} W[3]的形状是 (1, 3)
答案:
A.【 √ 】 W [ 1 ] W^{[1]} W[1]的形状是 (4, 4)
B.【 √ 】 b [ 1 ] b^{[1]} b[1]的形状是 (4, 1)
C.【 √ 】 W [ 2 ] W^{[2]} W[2]的形状是 (3, 4)
D.【 √ 】 b [ 2 ] b^{[2]} b[2]的形状是 (3, 1)
E.【 √ 】 b [ 3 ] b^{[3]} b[3]的形状是 (1, 1)
F.【 √ 】 W [ 3 ] W^{[3]} W[3]的形状是 (1, 3)
第十题
10.前面的问题使用了一个特定的网络,一般情况下,层 l l l的权重矩阵 W [ l ] W^{[l]} W[l]的维数是多少?
A. 【 】 W [ l ] W^{[l]} W[l]的形状是 ( n [ l ] , n [ l − 1 ] ) (n^{[l]},n^{[l-1]}) (n[l],n[l−1])
B. 【 】 W [ l ] W^{[l]} W[l]的形状是 ( n [ l − 1 ] , n [ l ] ) (n^{[l-1]},n^{[l]}) (n[l−1],n[l])
C. 【 】 W [ l ] W^{[l]} W[l]的形状是 ( n [ l + 1 ] , n [ l ] ) (n^{[l+1]},n^{[l]}) (n[l+1],n[l])
D. 【 】 W [ l ] W^{[l]} W[l]的形状是 ( n [ l ] , n [ l + 1 ] ) (n^{[l]},n^{[l+1]}) (n[l],n[l+1])
答案:
A.【 √ 】 W [ l ] W^{[l]} W[l]的形状是 ( n [ l ] , n [ l − 1 ] ) (n^{[l]},n^{[l-1]}) (n[l],n[l−1])