【基础算法训练】—— 01背包 + 排序

前言

零零散散的有几个专栏专栏，只是都没有成气候，我这儿了，可能蓝桥专栏，反响最好，只是受限制于自己的算法能力十分薄弱，就更得特别慢，也不全面吧，蓝桥现在是我的心头痛，我想暂时放一放，我自己也还在学，再次更那个专栏，可能有新的突破吧。千锤百炼，静待花开。


现在的单片机是会持续更的，因为我要靠它去捣腾暑假实习的事儿：十四天学会51单片机；
Leetcode的专栏会持续更，因为在跟着英雄哥做知识星球的事儿：在lc被欺负的这些年；
对英雄哥的知识星球有兴趣的可以看看他这篇文章喔： 英雄算法联盟 | 31天让你的算法与众不同

至于现在这专栏了，是我4月12号的想法，只是因为四月我整体比较痛苦，一直没有动工，现在开始动工啦~，迟到一个月。这个专栏只会记录全部是每日一题：知识星球每天的习题，以及在咱高校算法学习社区中，泡泡和p佬普及组和提高组的题目，一般是当天写次天更吧。

倘若对算法学习比较迷茫的小伙伴，可以考虑假如咱高校算法学习社区呀~

社区地址：高校算法学习社区


社区暂时有每日一题普及组以及提高组，由现役Acmer每日出题带领刷题，不会可群里随时提问喔。只是咱们拒绝划水党以及潜水党，需要的加入可私信执梗，也可以私信我哈。

第一题 977. 有序数组的平方

题目描述

原题传送门

解题报告

对于C++选手来说了，这个题应该不恼火，因为STL中提供了sort这个按照升序排序的函数，sort的时间复杂度是nlog2^n（log的底数选择默认的2）。题目的数据范围是10000，是不完全不会超时的。

参考代码(C++版本)

class Solution {
public:
    vector<int> sortedSquares(vector<int>& nums) {
        //常规的sort就是递增吧
        vector<int> ans;
        
        for(auto n : nums)
            ans.push_back(n*n);
        
        sort(ans.begin(),ans.end());
        return ans;
    }
};

第二题 268. 丢失的数字

浅记录异或

题目描述

原题传送门

解题报告

老老实实模拟的情况咱就不说了，C++的sort比C确实省了很多事儿。 看到一种用异或运算符来实现的玩法，浅记录一下。

异或是一个可交换顺序的操作。同一个数字异或两遍等于零。

也是先处理特殊情况吧。倘若最大的数字小于数组的长度，那么确实的数字是当前最大的数字+1；
处理完特殊情况，就进入咱们的异或环节了。
咱们在求最大值的时候可以顺带将数组的每个元素都异或一次，然后对0 ~ n中每个元素也异或一次，最后剩下的数字就是没有出现的数字了，因为其他都出现了两次。
比如样例中的[3，0，1]

参考代码(C++版本)

解法一：老老实实模拟

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        //从样例来分析了，是两种情况
        int len = nums.size();
        sort(nums.begin(),nums.end());
        int maxv = nums[len-1];
        int ans = 0;
        if(maxv != len) ans = len;
        
        for(int i = 1; i < len;i++)
            if(nums[i]-nums[i-1] != 1)
            {
                ans = nums[i]-1;
                break;
            }

        return ans;
    }
};

解法二：异或运算

class Solution {
public:
    int missingNumber(vector<int>& nums) {
        int n =0;
        int ans = 0;

        for(auto num:nums)
        {
            n = max(n,num);
            ans ^= num;
        }

        if(nums.size() > n) n = nums.size();

        for(int i = 0; i <= n;i++)
            ans ^= i;
        
        return ans;
    }
};

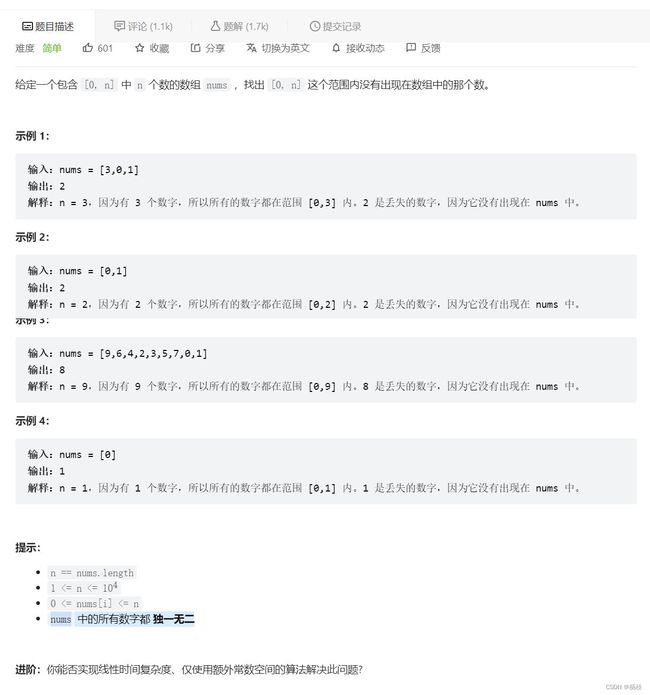
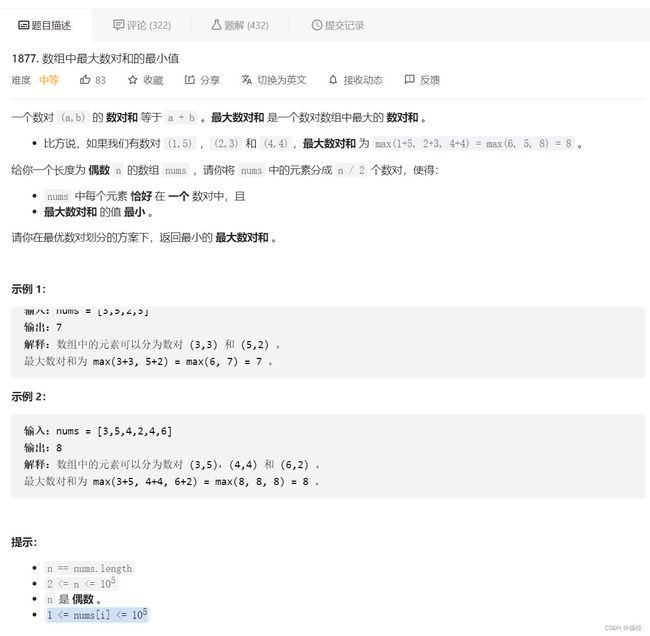
第三题 1877. 数组中最大数对和的最小值

生活智慧

题目描述

原题传送门

解题报告

STL真好…
题目的意思是这种的，给咱们一个长度为n(n是偶数)的数组，那么可以得到n/2个数对，然后这些组合中最大啊啊的数对和要求是所有组合方式中最小的，可能脑子里都立刻秦楚了，每次首和尾相加，这种得到的组合数对就是最小的了，然后最小的里面最大的结果，就是咱们要的答案。
这个题可以归纳成一个贪心的题，贪心的题，不妨说成是生活题，因为这种题咱一般可以直接通过直觉看出来，但是想要去证明这个直觉真的完全正确吗，就够呛了，贪心正是难在证明，比如让证明上面的思想真的可以吗，我暂时是证明不出来的。
看到宫水三叶大大写了证明，可以学习一下，我想后面再碰贪心的证明
【宫水三叶の相信科学系列】最大数对和的最小值，贪心解的正确性证明

参考代码(C++版本)

class Solution {
public:
    int minPairSum(vector<int>& nums) {
        //10^5，nlogn方向思考吧
        //先排序，然后两端双指针迭代吧
        sort(nums.begin(),nums.end());

        int l = 0, r = nums.size()-1;

        int maxv = -1;
        while(l < r)
        {
            maxv = max(maxv,nums[l]+nums[r]);
            l++,r--;
        }
        return maxv;
    }
};

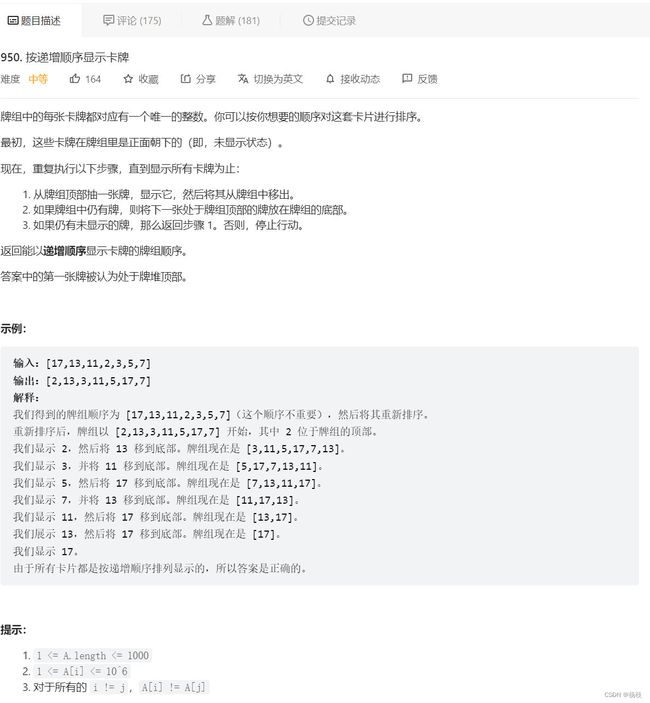
第四题 950. 按递增顺序显示卡牌

双端队列

题目描述

解题报告

这个题和蓝桥的巧排扑克牌有点小类似的巧排扑克牌
现在的情况是，题目给随便给我们一个序列[17,13,11,2,3,5,7]（这个顺序不重要），让咱们给出一个新的序列，这个序列可以根据题目逻辑构造出一个递增序列[2,3,5,7,11,13,17]，样例中的新序列是[2,13,3,11,5,17,7]。

既然可以根据结果[2,13,3,11,5,17,7]顺着题目逻辑推理出需要的[2,3,5,7,11,13,17]，
那么也一定可以通过[2,3,5,7,11,13,17]逆着题目逻辑推理出结果[2,13,3,11,5,17,7]

[2,13,3,11,5,17,7]是如何显示出[2,3,5,7,11,13,17]的了：
①显示 2，然后将 13 移到底部。牌组现在是 [3,11,5,17,7,13]。
②显示 3，并将 11 移到底部。牌组现在是 [5,17,7,13,11]。
③显示 5，然后将 17 移到底部。牌组现在是 [7,13,11,17]。
④显示 7，并将 13 移到底部。牌组现在是 [11,17,13]。
⑤显示 11，然后将 17 移到底部。牌组现在是 [13,17]。
⑥展示 13，然后将 17 移到底部。牌组现在是 [17]。
⑦显示 17。


现在倒着玩，让咱们可以直接获取到的[2,3,5,7,11,13,17]，倒着显示出[2,13,3,11,5,17,7]，也就是进行了求解。
①选择 17。插入17，牌组现在是 [17]。
②选择 13。先将 17 移到顶部，然后插入13。牌组现在是 [13，17]。
③选择 11。先将 17 移到顶部，然后插入11。牌组现在是 [11，17，13]。
④选择 7。先将 13 移到顶部，然后插入7。牌组现在是 [7，13，11,17]。
⑤选择 5。先将 17 移到顶部，然后插入5。牌组现在是 [5，17，7，13，11]。
⑥选择 3。先将 11 移到顶部，然后插入3。牌组现在是 [3，11，5，17，7，13]。
⑦选择 2。先将 13 移到顶部，然后插入3。牌组现在是 [2，13，3，11，5，17，7]。

现在的逻辑应该和清晰了，咱们在插入数据到序列之前，先把序列末尾的数据弹出放到序列首，再插入这个数据。
这种既需要对序列首操作，也需要对序列尾操作的，用双端队列挺香的

参考代码(C++版本)

参考代码一：

class Solution {
public:
    vector<int> deckRevealedIncreasing(vector<int>& deck) {
        int len = deck.size();
        //双端队列的声明
        deque<int> deq;
        vector<int> ans;
        if(len <= 2) return deck;
        //让现在有的序列排列
        sort(deck.begin(),deck.end());
        //序列的倒数第一和倒数第二个元素是可以直接插入的
        deq.push_front(deck[len-1]);
        deq.push_front(deck[len-2]);

        for(int i = len-3; i >= 0;i--)
        {
            //实现插入之前，先把序列尾部的元素放到序列首
            deq.push_front(deq.back());
            //将序列尾弹出
            deq.pop_back();
            //将这个准备插入的数据插入
            deq.push_front(deck[i]);
        }
        //将双端队列中的值，赋值到vector的数组中
        for(auto x : deq) ans.push_back(x);

        return ans;
    }
};

参考代码二：
发现一位佬用了蛮多的STL的方法，重载sort这儿想浅记录一下。
这种重载也是值得积累一下的。

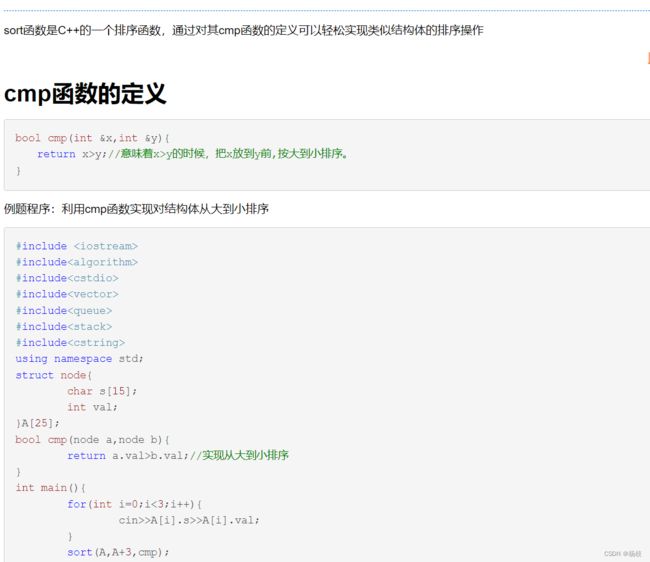
class Solution {
public:
    vector<int> deckRevealedIncreasing(vector<int>& deck) 
    {
        int n = deck.size();
        deque<int> seq;    
        //内置类型的由大到小排序
        //与之相对应的是less() ，内置类型的由小到大排序，sort默认是从小到大
        sort(deck.begin(),deck.end(),greater<int>());

        for(int i=0;i<n;++i)
        {
            if(!seq.empty())
            {
                seq.push_back(seq.front());
                seq.pop_front();
            }
            seq.push_back(deck[i]);
        }
        return vector<int>(seq.rbegin(),seq.rend());
    }
};

第五题 P1060 [NOIP2006 普及组] 开心的金明

01背包——空间逐渐优化

题目描述

原题传送门

解题报告

01背包的模板题了吧。自己也好一阵子没有碰动态规划了，也结合着提复习一下闫式DP分析法了。

先不阐述为什么用动态规划吧，现在好像解释不清楚，我只是看到一些题就觉得可以用动态规划，等我再多刷一点动态规划的题了，再来回复这个问题吧。

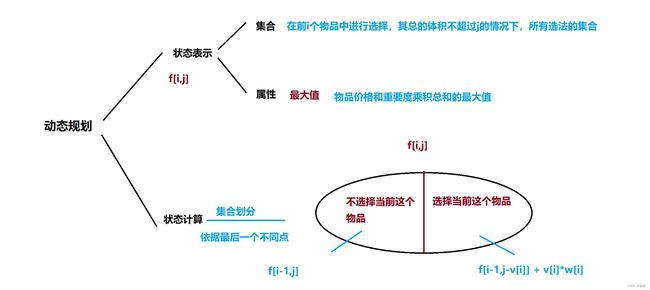
进入闫式DP的分析环节吧，闫式DP是将动态规划从集合的角度的思考。

步骤一：状态表示
① 集合定义：
集合的定义大多数情况下是根据问题描述进行定义一个数组。通俗点理解了，就是问题问什么，咱们就定义什么。01背包常规的定义了是数组f[i][j]表示前i个物品中选择，总体积不超过j的选法的集合。
对于这个题而言，集合定义是：[i][j]表示在前i个物品中选择，总金额不超过j的选法的集合
② 属性确定：
因为咱们定义的集合最终是一块内存空间，始终要存一个数据，这个数据和咱们定义的数据存在一定的联系，咱们就叫做它为属性了。

步骤二：状态计算
状态计算了，y总常说的是，对应状态划分的过程，划分的依旧是最后一个不同点。
就我自己的理解了，是这种的，观察当前这个状态i的前一个状态i-1是转移成i是否有什么不同点了。这里其实蛮依赖咱们的积累的。
对于01背包而言，从i-1转移到i的时候，可以选择拿当前这个物品i也可以选择不拿当前的


用一张图表示出来，就是如下的闫式DP分析图

参考代码(C++版本）

#include  

using namespace std;
const int N = 30010,M = 30;
int f[M][N];//在前m个物品中选择，总体积不超过n的选法的集合 
int v[M],w[M];//价格以及重要度 
int n,m;

int main()
{
	cin >> n >> m;
	
	//输入价格以及重要度 
	for(int i = 1;i <= m;i++) cin >> v[i] >> w[i] ;
	
	//开始DP——常规版本 
	for(int i = 1; i <= m;i++) 
		for(int j = 0; j <= n;j++)
		{
			f[i][j] = max(f[i-1][j],f[i][j]);
			if(j >= v[i]) f[i][j] = max(f[i-1][j-v[i]]+v[i]*w[i],f[i][j]);
		}
			
	cout << f[m][n];
	return 0;
}

上面这个代码是最朴素的，是可以出现优化版本的，动态规划是优化不了时间了，可以优化的只有空间了。
下面浅看一下滚动数组优化

#include  

using namespace std;
const int N = 30010,M = 30;
int f[2][N];//在前m个物品中选择，总体积不超过n的选法的集合 
int v[M],w[M];//价格以及重要度 
int n,m;

int main() 
{
	cin >> n >> m;
	
	for(int i = 1; i <= m;i++) cin >> v[i] >> w[i];
	
	for(int i = 1; i <= m;i++)
		for(int j = 0;j <= n;j++)
		{
			f[i&1][j] = f[(i-1)&1][j];
			if(j >= v[i]) f[i&1][j] = max(f[i&1][j],f[(i-1)&1][j-v[i]]+v[i]*w[i]);
		}
	int ans = 0;
	for(int j = 0; j <= n;j++)
		ans = max(ans,f[m&1][j]);
	
	cout << ans;
	return 0;
}

现在我们将阶段i的状态存储在第一维下标为i&1的二维数组中了。
当i为奇数的时候，i&1等于1；当是偶数的时候，i&1等于0。
此时整体的状态相当于在f[0][]和f[1][]之间交替滚动，空间复杂度成功的从$O(NM)$降低到了$O(M)$。


因为可以观察到，每个阶段而言，是执行了一次从f[i-1][]到f[i][]的拷贝操作，我的理解是，此时的递推是线性的，就能够实现到一维的优化。即当外层循环到第i个物品的时候，使用f[j]表示背包中放入总体积为j的物品价格和重要度的乘积的最大值。

#include  

using namespace std;
const int N = 30010,M = 30;
int [N];//在前m个物品中选择，总体积不超过n的选法的集合 
int v[M],w[M];//价格以及重要度 
int n,m;

int main() 
{
	cin >> n >> m;
	for(int i = 1;i <= m;i++)  cin >> v[i] >> w[i];
	
	for(int i =1; i <= m;i++)
		for(int j = n;j >= v[i];j--)
			f[j] = max(f[j],(f[j-v[i]]+v[i]*w[i]));
	
	cout << f[n];
}

可以发现，咱们的内层循环变成倒序循环了。记住我上面说的话，01背包的整体递推是从i-1向i的一个线性的递推。那咱们无论怎么变化，必须还是等保证整体是一个从 i-1到i转移的过程。
对于咱们的倒序循环而言，其满足这个转移过程可以通过下图来阐述

总结

排序的对有库函数的C++来说不是特别痛苦，只是个别时候可能需要重载sort(但也不是必要的操作)，我晚点补c的快排和归并玩法吧，
排序和贪心搞一块了，这儿我想浅注意一下~