ACwing:算法基础课 第二章单链表,双链表,队列,栈以及KMP听课笔记
前言
本次课程的前半部分讲链表和栈队列的时候都有多种的实现方式,比如可以通过用指针和结构体的方式去实现链表,也可以通过STL库直接实现栈和队列。但是本次课程主要就是讲用数组进行模拟,原因如下:
效率问题。通过数组模拟的效率比较高,如果利用结构体和指针实现链表的话,每次存进去的时候都要new一个结点,但是这个效率非常慢。一般都是有十万级别的,所以用动态链表去实现的时候,太耗时间了,全部都花在新建结点上面了。
如上图所示的这个动态存储的方式一般不用。但是如果进行优化一下还是可以用这个来实现的,优化的方式就是直接先初始化有多少个结点,就是不要去new了,这样的话这个原理就和数组差不多,省去了new的时间。
一。链表与邻接表
1。用数组模拟单链表,考得最多的是模拟邻接表的情况
(1)邻接表的作用
1⃣️存储图
2⃣️存储树
(2)数组模拟单链表的方法
首先需要两个数组e和ne,前者是用来存元素的,e的下标就表示结点的序号,内容就是表示该结点存的元素。ne 数组存的是下一个指向结点的位置,它的下标表示该结点的序号,里面存的是该结点指向的下一个结点的序号。

(3)模版代码如下:
1⃣️先设置出必要元素数组e,he,头指针head以及指针idx
2⃣️编写初始化函数。一开始head为-1,因为-1表示为链表尾的号码。IDX 为0,指向第一个。
3⃣️编写插入函数。
第一种插入情况:插入为头结点。分三步,第一步将数据存入到当前idx指向的结点e[idx]=new。第二步将新点的ne指向原来head指向的下一个结点位置。第三步head指回到新的头结点。第四步,idx++
第二种插入情况:将点插入到结点为k的点的后面。分四步走。第一步将新结点的数据存进来,e[idx]=new;第二步将新结点的ne 指向k结点的ne;第三步将k结点的ne指向新结点;第四步idx++

4⃣️编写删除结点函数。
第一种情况:将结点k后面的结点删除。直接将该结点k的ne指向厚厚一个,即ne[k]=ne[ne[k]];第二种情况:将头结点删除直接就是head=ne[head]即可
第二种情况的代码如下:
总的代码如下:
// head存储链表头,e[]存储节点的值,ne[]存储节点的next指针,idx表示当前用到了哪个节点
int head, e[N], ne[N], idx;
// 初始化
void init()
{
head = -1;
idx = 0;
}
// 在链表头插入一个数a,尾插法,head和idx一直往后运动
void insert(int a)
{
e[idx] = a, ne[idx] = head, head = idx ++ ;
}
// 将头结点删除,需要保证头结点存在
void remove()
{
head = ne[head];
}
2。用数组模拟双链表,考得最多的是用来优化某些问题
(1)用数组模拟双链表的方法
首先需要三个数组,e,l,r,e用来存这个该结点的元素是什么,l用来存该结点左边指向的是谁,r用来存该结点右边指向的是谁。然后还要一个 idx是用来作为遍历链表的指针,注意,我们直接将e[o]作为head,将最后一个结点作为tail
⚠️由于数组中的第0位和第1位已经当成了链表的最右端和最左端的端点,接下来每次都是往后面,实现双链表使用L,R的数组去引导,即E数组只是用于存储数据,实现链表指针的是R,L数组,此外,还要注意,比如在第K个插入的数后面在插入数据A,则插入的位置是K+2-1,因为数组的头两个已经存了。
(2)模版代码如下:
1⃣️设置必要的数组。
2⃣️编写初始化函数。
3⃣️编写插入函数。插入的时候可以插入右边也可以插入左边。
第一个情况:在k的右边插入一个新结点;分为五步走:第一步将结点的数据存进来e[idx]=new;第二步将新结点的右边指向原结点的右边;第三步将新结点的左边指向原结点的左边;第四步将原结点的下一个结点的左边指向新结点;第五步将原结点的右边指向新结点。
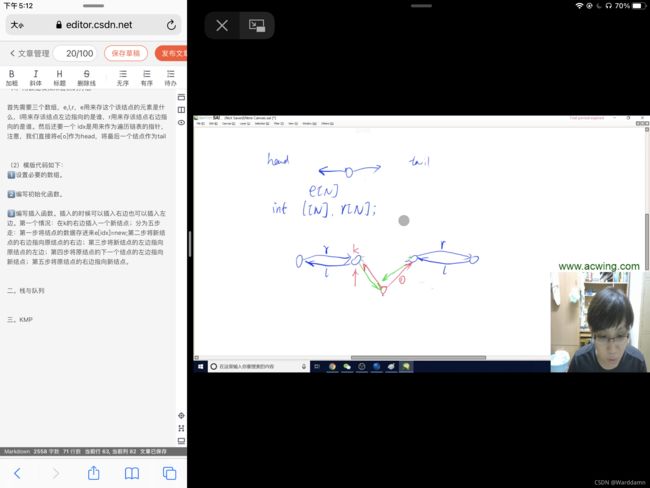
第二种情况,在k的左边插入一个新结点。直接变成在k的前一个结点的右边插入一个新结点就行,然后调用第一种情况的。
4⃣️编写删除函数。
直接将该结点的右边指向该结点的左边结点,将该结点的左边指向该结点的右边结点即可。

总的代码如下:
// e[]表示节点的值,l[]表示节点的左指针,r[]表示节点的右指针,idx表示当前用到了哪个节点
int e[N], l[N], r[N], idx;
// 初始化
void init()
{
//0是左端点,1是右端点
r[0] = 1, l[1] = 0;
idx = 2;
}
// 在节点a的右边插入一个数x
void insert(int a, int x)
{
e[idx] = x;
l[idx] = a, r[idx] = r[a];
l[r[a]] = idx, r[a] = idx ++ ;
}
// 删除节点a
void remove(int a)
{
l[r[a]] = l[a];
r[l[a]] = r[a];
}
二。栈与队列
1。栈与队列的定义:栈是先进后出,队列是先进先出。
2。栈的各种操作:直接用数组模拟,然后在用一个指针to 来指示。插入操作:stk[tt++]=x。弹出操作:tt—。判断栈是否为空:if(tt>0) not empty else empty 。栈顶:skt[tt]
// tt表示栈顶
int stk[N], tt = 0;
// 向栈顶插入一个数
stk[ ++ tt] = x;
// 从栈顶弹出一个数
tt -- ;
// 栈顶的值
stk[tt];
// 判断栈是否为空
if (tt > 0)
{
}
3。队列的各种操作:在队尾插入元素,队头弹出元素。q[N],hh,yy=-1。插入操作:q[++tt]=x;
弹出hh++; 判断队列是否为空:if(hh<=tt) not empty else empty;取出队头队尾元素q[hh],q[tt]。
// hh 表示队头,tt表示队尾
int q[N], hh = 0, tt = -1;
// 向队尾插入一个数
q[ ++ tt] = x;
// 从队头弹出一个数
hh ++ ;
// 队头的值
q[hh];
// 判断队列是否为空
if (hh <= tt)
{
}
循环队列:
// hh 表示队头,tt表示队尾的后一个位置
int q[N], hh = 0, tt = 0;
// 向队尾插入一个数
q[tt ++ ] = x;
if (tt == N) tt = 0;
// 从队头弹出一个数
hh ++ ;
if (hh == N) hh = 0;//就是只有这一步的区别
// 队头的值
q[hh];
// 判断队列是否为空
if (hh != tt)
{
}
4。单调栈:
(1)对应题型:给定一个序列,找出每个数的左边(右边)离他最近的,且比它小(大)的数在什么地方,例题如下:
(2) 暴力做法:
(3)优化做法:
首先,考虑是否具有单调性,假设从头开始出发的指针去扫描,因为找的是某个元素左边离他最近的最小的元素,所以扫描的时候如果新的元素比他大就不往前走了,因此,这具有单调性,我们可以用栈来实现,我们可以设置一个单调栈,就是,每次读入一个元素的时候,先将栈头的指针定位到比该元素小的最近的那个,如果栈顶指针不为空的话就说明已经找到最小的那个了,直接把结果输出去就行,然后把它加进单调栈里面,如果没找到的话,就输出-1即可然后比较一下,如果这个元素小的话就把它加进站里面
(4)本节学到的知识点(重点):
第一:单纯的cin,cout要比scanf慢十倍左右,所以如果输入输出很多的的话,还是非常建议用scanf才好
第二:在main函数中或者要用到cin ,cout的地方之前加上:
cin.tie(0);
ios::sync_with_stdio(false);
这样读入读出时间可以比拟 scanf
(5)总的代码如下:
常见模型:找出每个数左边离它最近的比它大/小的数
int tt = 0;
for (int i = 1; i <= n; i ++ )
{
while (tt && check(stk[tt], i)) tt -- ;
stk[ ++ tt] = i;
}
5。单调队列:
模板题:滑动窗口的是最大最小值
用队列来维护滑动窗口:第一步将滑动队列向右滑动滑动一位队头进来,然后队尾出去一位。发现单调性:依次遍历的时候,只要前面的点比后面的点要大那么就不可能被选上,所以就可以直接删去。这样就变成了一个单调队列。

单调队列和单调栈的一个思路都是:
先考虑这一题的朴素算法是啥,暴力模拟一边;然后在考虑这个朴素算法里面哪些元素是没有用的,把这些没有用的都删掉,接着看剩下的元素是否就构成了有单调性;如果有单调性就可以做优化——取极值就取两端,找元素就用二分。
注意:STL的容器若不开O2优化,则会比数组模拟的要2慢
常见模型:找出滑动窗口中的最大值/最小值
int hh = 0, tt = -1;
for (int i = 0; i < n; i ++ )
{
while (hh <= tt && check_out(q[hh])) hh ++ ; // 判断队头是否滑出窗口,注意由于q[hh]存的是原来数据数组的下标,所以就是要判断i-k+1这个表达式中,i表示当前的下标,k表示滑动窗口的长度,所以可以当前坐标的滑动窗口起点坐标,所以就是判断i-k+1>q[hh]的时候,就是已经滑出来了,要hh++;
while (hh <= tt && check(q[tt], i)) tt -- ;//出现更小值的下标,所以将原来的进行出队
q[ ++ tt] = i;//将更小的进队
}
总结:
一共分三步走:
1⃣️判断单调队列是否滑出窗口
2⃣️判断原数组的下一个元素是否比当前单调队列中的元素还要小,如果是的话,则一直出队
3⃣️将该原数组的元素进队
4⃣️输出结果:如果是求最大最小值则直接输出队首元素,也可以利用二分查找的等函数。注意,输出的时候,要保证此时的长度达到了滑动窗口的长度,即元素组的下标要达到长度。
滑动窗口例题的代码如下:

注意:判断滑动窗口是否滑出的时候,如果题目中一次就移动一个格,可以用if,但是如果题目中要求的是一次移多个格,就要用while
三。KMP
1.定义:
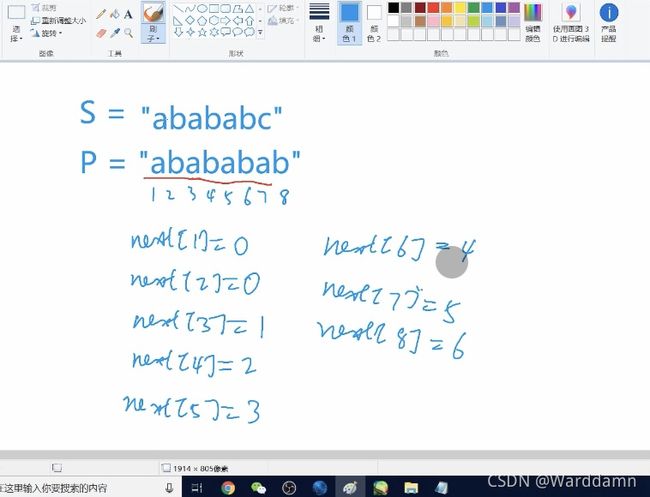
给出一个长串S[N]与以及一个模板串P[M],用模板串去匹配长串,如果长串中有包含模板串的部分,则输出true;
2.思考方向:
(1)先去思考暴力算法怎么做
(2)再去思考怎么去优化
3.暴力算法:
对模板串P[N]进行一个预处理,找出其以一个点的后缀与该点前缀相同的位置;这样子模板串去匹配长串的时候,如果匹配到长串的某一个位置失败了,那么就知道可以移动的最大长度了,因为我们找出了模板串中某个点后缀与该点前缀相同的位置。
这个就是KMP中next数组的含义,next[i]表示的这一段的字符串中后缀与以1为起点的前缀相等长度最长是多少
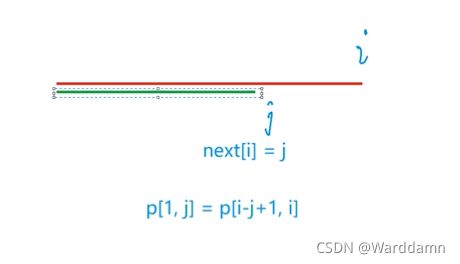
匹配过程如下:
5。代码如下:
注意点:
1⃣️S数组用来存长串数组,P数组用来存模版数组,且两者都是从1开始存数据
2⃣️在P匹配S数据的时候,为了保证不出错,都是统一用P[j+1]和S[i]进行匹配,因此扫描的时候,P数组是从0开始扫描,这样P[j+1]才是有值的,S数组是从1开始扫描,因为S 数组从1开始存数据
代码如下:
// s[]是长文本,p[]是模式串,n是s的长度,m是p的长度
求模式串的Next数组:
其实就是自己和自己匹配,一个P作为长串,一个P作为模版串
for (int i = 2, j = 0; i <= m; i ++ )
//i从2开始因为next[2]如果不成功就直接从头开始,即从i=1开始,所以没关系,直接从2开始即可
{
while (j && p[i] != p[j + 1]) j = ne[j];//该循环就是如果新的一位没有匹配成功,那么就一直跳next[],直到找到匹配成功的下一位或者挑到模版的首位为止
if (p[i] == p[j + 1]) j ++ ;//匹配成功
ne[i] = j;//因为是从1开始存数据的,所以j这个下标就表示了长度了
}
// 匹配
for (int i = 1, j = 0; i <= n; i ++ )
{
while (j && s[i] != p[j + 1]) j = ne[j];
if (s[i] == p[j + 1]) j ++ ;
if (j == m)
{
j = ne[j];
// 匹配成功后的逻辑,跳转到下一位ne[j]继续进行匹配
}
}