逻辑回归与评分卡

一、概述

1.名为“回归”的分类器
有不少带“回归”二字的算法，回归树，随机森林的回归，无一例外都是区别于分类算法们，用来处理和预测连续型标签的算法。然而逻辑回归，是一种名为“回归”的线性分类器，其本质是由线性回归变化而来的，一种广泛使用于分类问题中的广义回归算法。线性回归的方程写作：

θ被统称为模型的参数，其中θ0被称为截距(intercept)， θ1~θn被称为系数(coefficient)，这个表达式，其实就和y=ax+b是同样的性质。还可以用矩阵来表示这个方程，其中x和θ都可以被看做是一个列矩阵，则有：

线性回归的任务，就是构造一个预测函数z来映射输入的特征矩阵x和标签值y的线性关系，而**构造预测函数的核心就是找出模型的参数：θT 和θ0，**著名的最小二乘法就是用来求解线性回归中参数的数学方法。

通过函数z，线性回归使用输入的特征矩阵X来输出一组连续型的标签值y_pred，以完成各种预测连续型变量的任务（比如预测产品销量，预测股价等等）。那如果标签是离散型变量，尤其是，如果是满足0-1分布的离散型变量，要怎么办呢？可以通过引入联系函数(link function)，将线性回归方程z变换为g(z)，并且令g(z)的值分布在(0,1)之间，且当g(z)接近0时样本的标签为类别0，当g(z)接近1时样本的标签为类别1，这样就得到了一个分类模型。而这个联系函数对于逻辑回归来说，就是Sigmoid函数：

面试高危问题：Sigmoid函数的公式和性质
Sigmoid函数是一个S型的函数，当自变量z趋近正无穷时，因变量g(z)趋近于1，而当z趋近负无穷时，g(z)趋近于0，它能够将任何实数映射到(0,1)区间，使其可用于将任意值函数转换为更适合二分类的函数。
因为这个性质，Sigmoid函数也被当作是归一化的一种方法，与MinMaxSclaer同理，是属于数据预处理中的“缩放”功能，可以将数据压缩到[0,1]之内。区别在于，MinMaxScaler归一化之后，是可以取到0和1的（最大值归一化后就是1，最小值归一化后就是0），但Sigmoid函数只是无限趋近于0和1。

线性回归中z=θTx，于是将z带入，就得到了二元逻辑回归模型的一般形式：

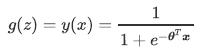
而y(x)就是逻辑回归返回的标签值。此时，y(x)的取值都在[0,1]之间，因此y(x)和1-y(x)相加必然为1，若令y(x)除以1-y(x)得到形似几率(odds)的y(x)/[1-y(x)]，在此基础上取对数，可以得到：

不难发现，y(x)的形似几率取对数的本质其实就是线性回归z，实际上是在对线性回归模型的预测结果取对数几率来让其的结果无限逼近0和1。因此，其对应的模型被称为”对数几率回归“（logistic Regression），也就是逻辑回归，这个名为“回归”却是用来做分类工作的分类器。

线性回归的核心任务是通过求解θ构建z这个预测函数，并希望预测函数z能够尽量拟合数据，因此逻辑回归的核心任务也是类似的：求解θ来构建一个能够尽量拟合数据的预测函数y(x)，并通过向预测函数中输入特征矩阵来获取相应的标签值y。

思考：y(x)代表了样本为某一类标签的概率吗？
lny(x)/[1-y(x)]是形似对数几率的一种变化。而几率odds的本质其实是p/[1-p]，其中p是事件A发生的概率，而1-p是事件A不会发生的概率，并且p+(1-p)=1。因此，很多人在理解逻辑回归时，都对y(x)做出如下的解释：

让线性回归结果逼近0和1，此时y(x)和1-y(x)之和为1，因此它们可以看作是一对正反例发生的概率，即y(x)是某样本i的标签被预测为1的概率，而1-y(x)是i的标签被预测为0的概率，y(x)/[1-y(x)] 就是样本i的标签被预测为1的相对概率。基于这种理解，使用最大似然法和概率分布函数推导出逻辑回归的损失函数，并且把返回样本在标签取值上的概率当成是逻辑回归的性质来使用，每当诉求概率的时候，都会使用逻辑回归。

然而这种理解是正确的吗？概率是度量偶然事件发生可能性的数值，尽管逻辑回归的取值在(0,1)之间，并且y(x)和1-y(x)之和的确为1，但光凭这个性质，就可以认为y(x)代表了样本x在标签上取值为1的概率吗？设想使用MaxMinScaler对特征进行归一化后，任意特征的取值也在[0,1]之间，并且任意特征的取值x0和1-x0也能够相加为1，但却不会认为0-1归一化后的特征是某种概率。逻辑回归返回了概率这个命题，这种说法严谨吗？

但无论如何，长年以来人们都是以”返回概率“的方式来理解逻辑回归，并且这样使用它的性质。可以说，逻辑回归返回的数字，即便本质上不是概率，却也有着概率的各种性质，可以被当成是概率来看待和使用。

2.为什么需要逻辑回归
线性回归对数据的要求很严格，比如标签、残差必须满足正态分布，特征之间的多重共线性需要消除等等，而现实中很多真实情景的数据无法满足这些要求，因此线性回归在很多现实情境的应用效果有限。逻辑回归是由线性回归变化而来，因此它对数据也有一些要求，而其他强大的分类模型如决策树和随机森林，它们的分类效力很强，并且不需要对数据做任何预处理。

何况，逻辑回归的原理其实并不简单。一个人要理解逻辑回归，必须要有一定的数学基础，必须理解损失函数，正则化，梯度下降，海森矩阵等等这些复杂的概念，才能够对逻辑回归进行调优。其涉及到的数学理念，不比支持向量机少多少。况且，要计算概率，朴素贝叶斯可以计算出真正意义上的概率，要进行分类，机器学习中能够完成二分类功能的模型简直多如牛毛。因此，在数据挖掘，人工智能所涉及到的医疗，教育，人脸识别，语音识别这些领域，逻辑回归没有太多的出场机会。

甚至，在各种机器学习经典书目中，周志华的《机器学习》400页仅有一页纸是关于逻辑回归的（还是一页数学公式），《数据挖掘导论》和《Python数据科学手册》中完全没有逻辑回归相关的内容，sklearn中对比各种分类器的效应也不带逻辑回归玩，可见业界地位。

但是，无论机器学习领域如何折腾，逻辑回归依然是一个受工业商业热爱，使用广泛的模型，因为它有着不可替代的优点：
1.逻辑回归对线性关系的拟合效果好到丧心病狂，特征与标签之间的线性关系极强的数据，比如金融领域中的信用卡欺诈，评分卡制作，电商中的营销预测等等相关的数据，都是逻辑回归的强项。虽然现在有了梯度提升树GDBT，比逻辑回归效果更好，也被许多数据咨询公司启用，但逻辑回归在金融领域，尤其是银行业中的统治地位依然不可动摇（相对的，逻辑回归在非线性数据的效果很多时候比瞎猜还不如，所以如果你已经知道数据之间的联系是非线性的，千万不要迷信逻辑回归）
2.**逻辑回归计算快：**对于线性数据，逻辑回归的拟合和计算都非常快，计算效率优于SVM和随机森林，亲测在大型数据上尤其能够看得出区别
3.逻辑回归返回的分类结果不是固定的0，1，而是以小数形式呈现的类概率数字：因此可以把逻辑回归返回的结果当成连续型数据来利用。比如在评分卡制作时，不仅需要判断客户是否会违约，还需要给出确定的”信用分“，而这个信用分的计算就需要使用类概率计算出的对数几率，而决策树和随机森林这样的分类器，可以产出分类结果，却无法计算分数（当然，在sklearn中，决策树也可以产生概率，使用接口predict_proba调用就好，但一般来说，正常的决策树没有这个功能）。

另外，逻辑回归还有抗噪能力强的优点。福布斯杂志有着“技术上来说，最佳模型的AUC面积低于0.8时，逻辑回归非常明显优于树模型”的说法。并且，逻辑回归在小数据集上表现更好，在大型的数据集上，树模型有着更好的表现。

由此，逻辑回归的本质，是一个返回对数几率的，在线性数据上表现优异的分类器，它主要被应用在金融领域。其数学目的是求解能够让模型对数据拟合程度最高的参数的值，以此构建预测函数，然后将特征矩阵输入预测函数来计算出逻辑回归的结果y。注意，虽然熟悉的逻辑回归通常被用于处理二分类问题，但逻辑回归也可以做多分类。
3.sklearn中的逻辑回归

逻辑回归相关的类	说明
linear_model.LogisticRegression	逻辑回归分类器（又叫logit回归，最大熵分类器）
linear_model.LogisticRegressionCV	带交叉验证的逻辑回归分类器
linear_model.logistic_regression_path	计算Logistic回归模型以获得正则化参数的列表
linear_model.SGDClassifier	利用梯度下降求解的线性分类器（SVM，逻辑回归等等）
linear_model.SGDRegressor	利用梯度下降最小化正则化后的损失函数的线性回归模型
metrics.log_loss	对数损失，又称逻辑损失或交叉熵损失
【在sklearn0.21版本中即将被移除】
linear_model.RandomizedLogisticRegression	随机的逻辑回归
其他会涉及的类	说明
metrics.confusion_matrix	混淆矩阵，模型评估指标之一
metrics.roc_auc_score	ROC曲线，模型评估指标之一
metrics.accuracy_score	精确性，模型评估指标之一

二、linear_model.LogisticRegression

class sklearn.linear_model.LogisticRegression (penalty=’l2’, dual=False, tol=0.0001, C=1.0,fit_intercept=True, intercept_scaling=1, class_weight=None, random_state=None, solver=’warn’, max_iter=100,multi_class=’warn’, verbose=0, warm_start=False, n_jobs=None)
1.二元逻辑回归的损失函数
1.1 损失函数的概念与解惑
在学习决策树和随机森林时，我们曾经提到过两种模型表现：在训练集上的表现，和在测试集上的表现。建模是追求模型在测试集上的表现最优，因此模型的评估指标往往是用来衡量模型在测试集上的表现的。然而，逻辑回归有着基于训练数据求解参数的需求，并且希望训练出来的模型能够尽可能地拟合训练数据，即模型在训练集上的预测准确率越靠近100%越好。
因此使用“损失函数”这个评估指标，来衡量参数为θ的模型拟合训练集时产生的信息损失的大小，并以此衡量参数的优劣。如果用一组参数建模后，模型在训练集上表现良好，就说模型拟合过程中的损失很小，损失函数的值很小，这一组参数就优秀；相反，如果模型在训练集上表现糟糕，损失函数就会很大，模型就训练不足，效果较差，这一组参数也就比较差。即是说在求解参数时，追求损失函数最小，让模型在训练数据上的拟合效果最优，即预测准确率尽量靠近100%。

关键概念：损失函数
衡量参数的优劣的评估指标，用来求解最优参数的工具。追求能够让损失函数最小化的参数组合
损失函数小，模型在训练集上表现优异，拟合充分，参数优秀
损失函数大，模型在训练集上表现差劲，拟合不足，参数糟糕
注意：没有”求解参数“需求的模型没有损失函数，比如KNN，决策树

逻辑回归的损失函数是由极大似然估计推导出来的，具体结果可以写作：

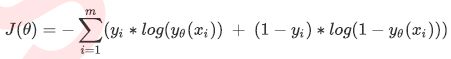
其中， θ表示求解出来的一组参数，m是样本的个数， y_i是样本i上真实的标签，y_θ(x_i) 是样本i上，基于参数θ计算出来的逻辑回归返回值，x_i是样本i各个特征的取值。目标是求解出使J(θ)最小的θ取值。注意，在逻辑回归的本质函数y(x)里，特征矩阵x是自变量，参数是θ。但在损失函数中，参数θ是损失函数的自变量，x和y都是已知的特征矩阵和标签，相当于是损失函数的参数。不同的函数中，自变量和参数各有不同，因此大家需要在数学计算中，尤其是求导的时候避免混淆。

由于追求损失函数的最小值，让模型在训练集上表现最优，可能会引发另一个问题：如果模型在训练集上表示优秀，却在测试集上表现糟糕，模型就会过拟合。虽然逻辑回归和线性回归是天生欠拟合的模型，但还是需要控制过拟合的技术来帮助调整模型，对逻辑回归中过拟合的控制，通过正则化来实现。

1.2【选学】二元逻辑回归损失函数的数学解释，公式推导与解惑
虽然质疑过”逻辑回归返回概率“这样的说法，但不可否认逻辑回归的整个理论基础都是建立在这样的理解上的。这里基于极大似然法来推导二元逻辑回归的损失函数，这个推导过程能够帮助了解损失函数是怎么得来的，以及为什么J(θ)的最小化能够实现模型在训练集上的拟合最好。

请时刻记得目标：让模型对训练数据的效果好，追求损失最小。

二元逻辑回归的标签服从伯努利分布(即0-1分布)，因此可以将一个特征向量为x，参数为θ的模型中的一个样本
i的预测情况表现为如下形式：
样本i在由特征向量x_i和参数θ组成的预测函数中，样本标签被预测为1的概率为：

样本i在由特征向量x_i和参数θ组成的预测函数中，样本标签被预测为0的概率为：

当P₁的值为1的时候，代表样本i的标签被预测为1，当P₀的值为1的时候，代表样本i的标签被预测为0。

假设样本i的真实标签为1，此时如果P₁为1，P₀为0，就代表样本i的标签被预测为1，与真实值一致，对于单样本i来说，模型的预测就是完全准确的，拟合程度很优秀，没有任何信息损失。相反，如果P₁此时为0，P₀为1，就代表样本i的标签被预测为0，与真实情况完全相反。对于单样本i来说，模型的预测就是完全错误的，拟合程度很差，所有的信息都损失了。
当y_i为0时，也是同样的道理。所以，当y_i为1的时候，希望P₁非常接近1，当y_i为0时，希望P₀非常接近1，这样，模型的效果就很好，信息损失就很少。

真实标签yi	被预测为1的概率P1	被预测为0的概率P0	样本被预测为	与真实值一致吗？	拟合状况	信息损失
1	0	1	0	否	坏	大
1	1	0	1	是	好	小
0	0	1	0	是	好	小
0	1	0	1	否	坏	大

将两种取值的概率整合，我们可以定义如下等式：

这个等式同时代表了P₁和P₀。
当样本i的真实标签y_i为1的时候，1-y_i就等于0，P₀的0次方就是1，所以等式就等于P₁，这个时候，如果P₁为1，模型的效果就很好，损失就很小。
同理，当y_i为0的时候，等式就等于P₀，此时如果P₀非常接近1，模型的效果就很好，损失就很小。
**所以，为了达成让模型拟合好，损失小的目的，每时每刻都希望等式的值等于1。**而等式左边的本质是样本i由特征向量x_i和参数θ组成的预测函数中，预测出所有可能的y^–_i的概率，因此1是它的最大值。**也就是说，每时每刻都在追求等式左边的最大值。**这就将模型拟合中的“最小化损失”问题，转换成了对函数求解极值的问题。

等式左边是对单个样本i而言的函数，对一个训练集的m个样本来说，可以定义如下等式来表达所有样本在特征矩阵X和参数θ组成的预测函数中，预测出所有可能的y^–的概率P为：

对该概率P取对数，再由log(A*B)=logA+logB和logA^B=BlogA可得到：

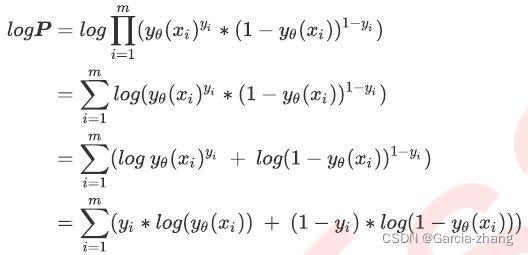
这就是交叉熵函数。为了数学上的便利以及更好地定义”损失”的含义，希望将极大值问题转换为极小值问题，因此对logP取负，并且让参数θ作为函数的自变量，就得到了损失函数J(θ)：

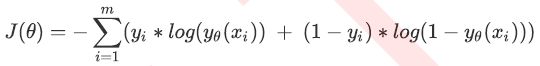
这就是一个，基于逻辑回归的返回值y_θ(x_i)的概率性质得出的损失函数。**在这个函数上，只要追求最小值，就能让模型在训练数据上的拟合效果最好，损失最低。**这个推导过程，其实就是“极大似然法”的推导过程。

关键概念：似然与概率
似然与概率是一组非常相似的概念，它们都代表着某件事发生的可能性，但它们在统计学和机器学习中有着微妙的不同。以样本i为例，有表达式：
对这个表达式而言，如果参数θ是已知的，特征向量xi是未知的，便称P是在探索不同特征取值下获取所有可能的y–的可能性，这种可能性就被称为概率，研究的是自变量和因变量之间的关系。
如果特征向量xi是已知的，参数θ是未知的，便称P是在探索不同参数下获取所有可能的y–的可能性，这种可能性就被称为似然，研究的是参数取值与因变量之间的关系。
在逻辑回归的建模过程中，特征矩阵是已知的，参数是未知的，因此讨论的所有“概率”其实严格来说都应该是“似然”。追求的最大值（换算成损失函数之后取负了，所以是最小值），就是在追求“极大似然”，所以逻辑回归的损失函数的推导方法叫做”极大似然法“。也因此，以下式子又被称为”极大似然函数“：

2.重要参数penalty & C
2.1 正则化
正则化是用来防止模型过拟合的过程，常用的有L1正则化和L2正则化两种选项，分别通过在损失函数后加上参数向量θ的L1范式和L2范式的倍数来实现。这个增加的范式，被称为“正则项”，也被称为"惩罚项"。损失函数改变，基于损失函数的最优化来求解的参数取值必然改变，以此来调节模型拟合的程度。其中L1范式表现为参数向量中的每个参数的绝对值之和，L2范数表现为参数向量中的每个参数的平方和的开方值。

其中J(θ)是之前提过的损失函数，C是用来控制正则化程度的超参数，n是方程中特征的总数，也是方程中参数的总数，j代表每个参数。在这里，j要大于等于1，是因为参数向量θ中，第一个参数是θ₀，是截距，通常是不参与正则化的。
也可以写成如下形式：

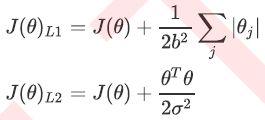
其实和上面的式子的本质是一模一样的。不过在大多数教材和博客中，常数项是乘以正则项，通过调控正则项来调节对模型的惩罚。而sklearn当中，常数项C是在损失函数的前面，通过调控损失函数本身的大小，来调节对模型的惩罚。

参数	说明
penalty	可以输入"l1"或"l2"来指定使用哪一种正则化方式，不填写默认"l2"。注意，若选择"l1"正则化，参数solver仅能够使用求解方式”liblinear"和"saga“，若使用“l2”正则化，参数solver中所有的求解方式都可以使用。
C	C正则化强度的倒数，必须是一个大于0的浮点数，不填写默认1.0，即默认正则项与损失函数的比值是1:1。C越小，损失函数会越小，模型对损失函数的惩罚越重，正则化的效力越强，参数θ会逐渐被压缩得越来越小

L1正则化和L2正则化虽然都可以控制过拟合，但它们的效果并不相同。当正则化强度逐渐增大（即C逐渐变小），参数θ的取值会逐渐变小，但L1正则化会将参数压缩为0，L2正则化只会让参数尽量小，不会取到0。

在L1正则化在逐渐加强的过程中，携带信息量小的、对模型贡献不大的特征的参数，会比携带大量信息的、对模型有巨大贡献的特征的参数更快地变成0，所以L1正则化本质是一个特征选择的过程，掌管了参数的“稀疏性”。L1正则化越强，参数向量中就越多的参数为0，参数就越稀疏，选出来的特征就越少，以此来防止过拟合。因此，如果特征量很大，数据维度很高，会倾向于使用L1正则化。由于L1正则化的这个性质，逻辑回归的特征选择可以由Embedded嵌入法来完成。

相对的，L2正则化在加强的过程中，会尽量让每个特征对模型都有一些小的贡献，但携带信息少，对模型贡献不大的特征的参数会非常接近于0。通常来说，如果主要目的只是为了防止过拟合，选择L2正则化就足够了。但是如果选择L2正则化后还是过拟合，模型在未知数据集上的效果表现很差，就可以考虑L1正则化。

而两种正则化下C的取值，都可以通过学习曲线来进行调整。

建立两个逻辑回归，L1正则化和L2正则化的差别就一目了然了：

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

data = load_breast_cancer()
X = data.data
y = data.target
print(data.data.shape)

lrl1 = LR(penalty="l1",solver="liblinear",C=0.5,max_iter=1000)
lrl2 = LR(penalty="l2",solver="liblinear",C=0.5,max_iter=1000)
#逻辑回归的重要属性coef_，查看每个特征所对应的参数
lrl1 = lrl1.fit(X,y)#实例化
print(lrl1.coef_)
print((lrl1.coef_ != 0).sum(axis=1))#返回系数不为0的特征的个数
lrl2 = lrl2.fit(X,y)
print(lrl2.coef_)
#可以看出，当选择L1正则化的时候，许多特征的参数被设置成了0，这些特征在真正建模的时候，就不会出现在模型中了；
#而L2正则化是对所有特征都给出了参数
l1 = []
l2 = []
l1test = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)#划分训练集和测试集
for i in np.linspace(0.05,1,19):#0.05~1之间取19个数
    lrl1 = LR(penalty="l1",solver="liblinear",C=i,max_iter=1000)
    lrl2 = LR(penalty="l2",solver="liblinear",C=i,max_iter=1000)
    lrl1 = lrl1.fit(Xtrain,Ytrain)
    l1.append(accuracy_score(lrl1.predict(Xtrain),Ytrain))
    l1test.append(accuracy_score(lrl1.predict(Xtest),Ytest))
    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l1,l2,l1test,l2test]
color = ["green","black","lightgreen","gray"]
label = ["L1","L2","L1test","L2test"]
plt.figure(figsize=(6,6))
for i in range(len(graph)):#i最大为4
    plt.plot(np.linspace(0.05,1,19),graph[i],color[i],label=label[i])
plt.legend(loc=4) #loc为location,表示图例的位置在哪里?4表示图例放在右下角。光标放在loc前面，用shift+tab可以查看
plt.show()
#模型在训练集上表现很好，但是在测试集上表现略欠，有轻微的过拟合，但是不严重
#当C逐渐增大，对模型的惩罚越来越小，正则化和损失函数的比例越来越接近1:1
#当C逐渐增大，训练集的表现一直在上升，模型拟合程度越来越高，但测试集从C=0.5以后就没有明显的上升了

#可见，至少在乳腺癌数据集下，两种正则化的结果区别不大。但随着C的逐渐变大，正则化的强度越来越小，模型在训练集和测试集上的表现都呈上升趋势，直到C=0.8左右，训练集上的表现依然在走高，但模型在未知数据集上的表现开始下跌，这时候就是出现了过拟合。因此可以认为，C设定为0.8会比较好。在实际使用时，基本就默认使用l2正则化，如果感觉到模型的效果不好，那就换L1试试。

2.2 逻辑回归中的特征工程
当特征的数量很多的时候，出于业务考虑，也出于计算量的考虑，希望对逻辑回归进行特征选择来降维。比如，在判断一个人是否会患乳腺癌的时候，医生如果看5~8个指标来确诊，会比需要看30个指标来确诊容易得多。
业务选择
说到降维和特征选择，首先要想到的是利用自己的业务能力进行选择，肉眼可见明显和标签有关的特征就是需要留下的。当然，如果并不了解业务，或者有成千上万的特征，那也可以使用算法来帮忙。或者，可以让算法先筛选过一遍特征，然后在少量的特征中，再根据业务常识来选择更少量的特征。
PCA和SVD一般不用
说到降维，首先想到的是之前提过的高效降维算法，PCA和SVD，遗憾的是，这两种方法大多数时候不适用于逻辑回归。逻辑回归是由线性回归演变而来，线性回归的一个核心目的是通过求解参数来探究特征X与标签y之间的关系，而逻辑回归也传承了这个性质，常常希望通过逻辑回归的结果，来判断什么样的特征与分类结果相关，因此希望保留特征的原貌。PCA和SVD的降维结果是不可解释的，因此一旦降维后，就无法解释特征和标签之间的关系了。当然，在不需要探究特征与标签之间关系的线性数据上，降维算法PCA和SVD也是可以使用的。
统计方法可以使用，但不是非常必要
既然降维算法不能使用，要用的就是特征选择方法。逻辑回归对数据的要求低于线性回归，由于不是使用最小二乘法来求解，所以逻辑回归对数据的总体分布和方差没有要求，也不需要排除特征之间的共线性，但如果确实希望使用一些统计方法，比如方差，卡方，互信息等方法来做特征选择，也并没有问题。过滤法中所有的方法，都可以用在逻辑回归上。

在一些博客中有这样的观点：多重共线性会影响线性模型的效果。对于线性回归来说，多重共线性会影响比较大，所以需要使用方差过滤和方差膨胀因子VIF(variance inflation factor)来消除共线性。但是对于逻辑回归，其实不是非常必要，甚至有时候，还需要多一些相互关联的特征来增强模型的表现。当然，如果无法通过其他方式提升模型表现，并且感觉到模型中的共线性影响了模型效果，那可以试试看用VIF消除共线性的方法，遗憾的是现在sklearn中并没有提供VIF的功能。

R vs Python，统计学 vs 机器学习
R中有各种各样的统计功能，而python的统计学功能并不是那么全面。(在jupyter中输入 import this 可以查看python制作者所写的诗歌”python之禅“)
为什么python和R在统计学的功能上差异如此之大呢？也许大家听说过，R是学统计学的人开发的，因此整个思路都是统计学的思路，而python是学计算机的人开发的，因此整个思路都是计算机的思路，也无怪R在处理统计问题上比python强很多了，这两种学科不同的思路强烈反应在统计学和机器学习的各种建模流程当中。
统计学的思路是一种“先验”的思路，不管做什么都要先”检验“，先”满足条件“，事后也要各种”检验“，以确保各种数学假设被满足，不然的话，理论上就无法得出好结果。而机器学习是一种”后验“的思路，不管三七二十一，先让模型跑一跑，效果不好再想办法，如果模型效果好，完全不在意什么共线性，残差不满足正态分布，没有哑变量之类的细节，模型效果好大过天！
完全欣赏机器学习的这种”后验“思路：我们追求结果，不要过于在意那些需要满足的先决条件。统计学是机器学习穷尽所有手段都无法解决问题后的”救星“，如果机器学习不能解决问题，会向统计学寻求帮助，但我绝不会一开始就想着要去满足各种统计要求。当然,统计学和机器学习是相辅相成的，大家要了解两种思路的不同，以便在进入死胡同的时候，可以从另一学科的思路中找到出路。

高效的嵌入法embedded
但是更有效的方法，毫无疑问会是embedded嵌入法。由于L1正则化会使得部分特征对应的参数为0，因此L1正则化可以用来做特征选择，结合嵌入法的模块SelectFromModel，可以很容易就筛选出让模型十分高效的特征。注意，此时目的是，尽量保留原数据上的信息，让模型在降维后的数据上的拟合效果保持优秀，因此不考虑训练集测试集的问题，把所有的数据都放入模型进行降维。

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel

data = load_breast_cancer()
print(data.data.shape)

LR_ = LR(solver="liblinear",C=0.9,random_state=420)
print(cross_val_score(LR_,data.data,data.target,cv=10).mean())
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)#norm_order=1表示使用L1范式
print(X_embedded.shape)
print(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())
#特征数量被减小到个位数，并且模型的效果却没有下降太多，如果要求不高，在这里其实就可以停下了。
#如果想让模型的拟合效果更好，有两种调整方式：

**1）**调节SelectFromModel这个类中的参数threshold，这是嵌入法的阈值，表示删除所有参数的绝对值低于这个阈值的特征。现在threshold默认为None，所以SelectFromModel只根据L1正则化的结果来选择了特征，即选择了所有L1正则化后参数不为0的特征。此时，只要调整threshold的值（画出threshold的学习曲线），就可以观察不同的threshold下模型的效果如何变化。一旦调整threshold，就不是在使用L1正则化选择特征，而是使用模型的属性.coef_中生成的各个特征的系数来选择。coef_虽然返回的是特征的系数，但是系数的大小和决策树中的feature_ importances_以及降维算法中的可解释性方差explained_vairance_概念相似，其实都是衡量特征的重要程度和贡献度的，因此SelectFromModel中的参数threshold可以设置为coef_的阈值，即可以剔除系数小于threshold中输入的数字的所有特征。

fullx = []
fsx = []

threshold = np.linspace(0,abs((LR_.fit(data.data,data.target).coef_)).max(),20)#abs((LR_.fit(data.data,data.target).coef_)).max()系数绝对值的最大值

k=0
for i in threshold:
    X_embedded = SelectFromModel(LR_,threshold=i).fit_transform(data.data,data.target)
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=5).mean())
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=5).mean())
    print((threshold[k],X_embedded.shape[1]))
    k+=1

plt.figure(figsize=(20,5))
plt.plot(threshold,fullx,label="full")
plt.plot(threshold,fsx,label="feature selection")
plt.xticks(threshold)
plt.legend()
plt.show()
#然而这种方法其实是比较无效的，用学习曲线跑一跑：当threshold越来越大，被删除的特征越来越多，模型的效果也越来越差，模型效果最好的情况下需要保证有17个以上的特征。实际上画了细化的学习曲线后发现，如果要保证模型的效果比降维前更好，需要保留25个特征，这对于现实情况来说，是一种无效的降维：需要30个指标来判断病情，和需要25个指标来判断病情，对医生来说区别不大。

**2）**第二种调整方法，是调逻辑回归的类LR_，通过画C的学习曲线来实现：

fullx = []
fsx = []

C=np.arange(0.01,10.01,0.5)
for i in C:
    LR_ = LR(solver="liblinear",C=i,random_state=420)
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())
    X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())
print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label="full")
plt.plot(C,fsx,label="feature selection")
plt.xticks(C)
plt.legend()
plt.show()

继续细化

fullx = []
fsx = []
C=np.arange(4.05,5.05,0.005)
for i in C:
    LR_ = LR(solver="liblinear",C=i,random_state=420)
    fullx.append(cross_val_score(LR_,data.data,data.target,cv=10).mean())
    X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
    fsx.append(cross_val_score(LR_,X_embedded,data.target,cv=10).mean())
print(max(fsx),C[fsx.index(max(fsx))])
plt.figure(figsize=(20,5))
plt.plot(C,fullx,label="full")
plt.plot(C,fsx,label="feature selection")
plt.xticks(C)
plt.legend()
plt.show()
#验证模型效果：降维之前
LR_ = LR(solver="liblinear",C=6.069999999999999,random_state=420)
cross_val_score(LR_,data.data,data.target,cv=10).mean()
#验证模型效果：降维之后
LR_ = LR(solver="liblinear",C=6.069999999999999,random_state=420)
X_embedded = SelectFromModel(LR_,norm_order=1).fit_transform(data.data,data.target)
cross_val_score(LR_,X_embedded,data.target,cv=10).mean()
print(X_embedded.shape)

这样就实现了在特征选择的前提下，保持模型拟合的高效，现在，如果有一位医生可以来指点迷津，看看剩下的这些特征中，有哪些是对针对病情来说特别重要的，也许还可以继续降维。当然，除了嵌入法，系数累加法或者包装法也是可以使用的。
比较麻烦的系数累加法
系数累加法的原理非常简单。在PCA中，通过绘制累积可解释方差贡献率曲线来选择超参数，在逻辑回归中可以使用系数coef_来这样做，并且选择特征个数的逻辑也是类似的：找出曲线由锐利变平滑的转折点，转折点之前被累加的特征都是需要的，转折点之后的都不需要。不过这种方法相对比较麻烦，因为要先对特征系数进行从大到小的排序，还要确保知道排序后的每个系数对应的原始特征的位置，才能够正确找出那些重要的特征。如果要使用这样的方法，不如直接使用嵌入法来得方便。
简单快速的包装法
相对的，包装法可以直接设定我们需要的特征个数，逻辑回归在现实中运用时，可能会有”需要5~8个变量”这种需
求，包装法此时就非常方便了。不过逻辑回归的包装法的使用和其他算法一样，并不具有特别之处，因此在这里就
不在赘述，具体大家可以参考03期：数据预处理和特征工程中的代码。
3.梯度下降：重要参数max_iter
逻辑回归的数学目的是求解能够让模型最优化，拟合程度最好的参数的值，即求解能够让损失函数J(θ)最小化的值。对于二元逻辑回归来说，有多种方法可以用来求解参数θ，最常见的有梯度下降法(Gradient Descent)，坐标下降法(Coordinate Descent)，牛顿法(Newton-Raphson method)等，其中又以梯度下降法最为著名。每种方法都涉及复杂的数学原理，但这些计算在执行的任务其实是类似的。
3.1 梯度下降求解逻辑回归
以最著名也最常用的梯度下降法为例，来看看逻辑回归的参数求解过程究竟实在做什么。
现在有一个带两个特征并且没有截距的逻辑回归y(x₁,x₂)，两个特征所对应的参数分别为[θ₁,θ₂]。下面这个华丽的平面就是损失函数J(θ₁,θ₂)在以θ₁,θ₂和J为坐标轴的三维立体坐标系上的图像。现在寻求的是损失函数的最小值，也就是图像的最低点。

在这个图像上随机放一个小球，当松手，这个小球就会顺着这个华丽的平面滚落，直到滚到深蓝色的区域——损失函数的最低点。为了严格监控这个小球的行为，让小球每次滚动的距离有限，不让他一次性滚到最低点，并且最多只允许它滚动100步，还要记下它每次滚动的方向，直到它滚到图像上的最低点。

可以看见，小球从高处滑落，在深蓝色的区域中来回震荡，最终停留在了图像凹陷处的某个点上。非常明显，可以观察到几个现象：

首先，小球并不是一开始就直向着最低点去的，它先一口气冲到了蓝色区域边缘，后来又折回来，已经规定了小球是多次滚动，所以可见，小球每次滚动的方向都是不同的。

另外，小球在进入深蓝色区域后，并没有直接找到某个点，而是在深蓝色区域中来回震荡了数次才停下。这有两种可能：1) 小球已经滚到了图像的最低点，所以停下了，2) 由于设定的步数限制，小球还没有找到最低点，但也只好在100步的时候停下了。也就是说，小球不一定滚到了图像的最低处。

但无论如何，小球停下的就是现有状况下可以获得的唯一点了。如果够幸运，这个点就是图像的最低点，那只要找到这个点的对应坐标(θ^*₁,θ^*₂,J_min)，就可以获取能够让损失函数最小的参数取值[θ^*₁,θ^*₂]了。如此，梯度下降的过程就已经完成。

在这个过程中，**小球其实就是一组组的坐标点(θ₁,θ₂,J)；小球每次滚动的方向就是那一个坐标点的梯度向量的方向，**因为每滚动一步，小球所在的位置都发生变化，坐标点和坐标点对应的梯度向量都发生了变化，所以每次滚动的方向也都不一样；人为设置的100次滚动限制，就是sklearn中逻辑回归的参数max_iter，代表着能走的最大步数，即最大迭代次数。

所以梯度下降，其实就是在众多[θ₁,θ₂]可能的值中遍历，一次次求解坐标点的梯度向量，不断让损失函数的取值J
逐渐逼近最小值，再返回这个最小值对应的参数取值[θ^*₁,θ^*₂]的过程。
3.2 梯度下降的概念与解惑
在多元函数上对各个自变量求∂偏导数，把求得的各个自变量的偏导数以向量的形式写出来，就是梯度。

比如损失函数J(θ₁,θ₂)，其自变量是逻辑回归预测函数y_θ(x)的参数θ₁,θ₂，在损失函数上对θ₁,θ₂求偏导数，求得的梯度向量d就是[∂J/∂θ₁,∂J/∂θ₂]^T，简称gradJ(θ₁,θ₂)或者▽J(θ₁,θ₂)。在θ₁,θ₂和J的取值构成的坐标系上，点(θ^*₁,θ^*₂,J_min)具体的梯度向量就是[∂J/∂θ^*₁,∂J/∂θ^*₂]^T，或者▽J(θ^*₁,θ^*₂)。如果是3个参数的梯度向量，就是[∂J/∂θ₁,∂J/∂θ₂,∂J/∂θ₃]^T，以此类推。

核心误区：到底在哪个函数上，求什么的偏导数？
在一些博客或教材中，讲解梯度向量的定义时会写一些让人容易误解的句子，比如“对多元函数的参数求∂偏导数，把求得的各个参数的偏导数以向量的形式写出来，就是梯度”。注意，这种解释一眼看上去没错，却是不太严谨的。
**一个多元函数的梯度，是对其自变量求偏导的结果，不是对其参数求偏导的结果。**但是在逻辑回归的数学过程中，损失函数的自变量刚好是逻辑回归的预测函数y(x)的参数，所以才造成了这种让人误解的，“对多元函数的参数求偏导”的写法。务必记住，正确的做法是：在多元函数(损失函数)上对自变量(逻辑回归的预测函数y(x)的参数)求偏导，求解梯度的方式，和逻辑回归本身的预测函数y(x)没有一丝联系。
以及，有一些博客会以f(x,y)作为例子，解释说梯度向量是(∂f/∂x,∂f/∂y)T。这种举例方式又会造成误解：很多人看到这个式子，会特别自然地理解成：“ x是逻辑回归中的特征呀，所以梯度向量是对模型的特征，即x求偏导数”。这个例子，其实是在表明，是对多元函数的自变量求偏导数，并不是代表在逻辑回归中要对特征求偏导数。
在这里强调：求解梯度，是在损失函数J(θ1,θ2)上对损失函数自身的自变量θ1和θ2求偏导，而这两个自变量，刚好是逻辑回归的预测函数的参数。

梯度是一个向量，因此它有大小也有方向。它的大小，就是偏导数组成的向量的大小，又叫做向量的模，记作d。它的方向，几何上来说，就是损失函数J(θ)的值增加最快的方向，就是小球每次滚动的方向的反方向。只要沿着梯度向量的反方向移动坐标，损失函数J(θ)的取值就会减少得最快，也就最容易找到损失函数的最小值。

在逻辑回归中，损失函数如下所示：

对这个函数上的自变量θ求偏导，就可以得到梯度向量在第j组θ的坐标点上的表示形式：

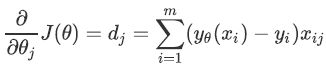
在这个公式下，只要给定一组θ的取值θ_j，再带入特征矩阵x，就可以求得这一组θ取值下的预测结果y_θ(x_i)，结合
真实标签向量y，就可以获得这一组θ_j取值下的梯度向量，其大小表示为d_j。之前说过，目的是在可能的θ取值上进行遍历，一次次计算梯度向量，并在梯度向量的反方向上让损失函数J下降至最小值。在这个过程中，θ和梯度向量的大小d都会不断改变，而遍历θ的过程可以描述为：

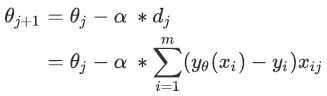
其中θ_j+1是第j次迭代后的参数向量，θ_j是第j次迭代时的参数向量，α被称为步长，控制着每走一步（每迭代一次）后θ的变化，并以此来影响每次迭代后的梯度向量的大小和方向。
3.3 步长的概念与解惑

步长到底是什么？
许多博客和教材在描述步长的时候，声称它是”梯度下降中每一步沿梯度的反方向前进的长度“，”沿着最陡峭最易下山的位置走的那一步的长度“或者”梯度下降中每一步损失函数减小的量“，甚至有说，步长是二维平面著名的求导三角形中的”斜边“或者“对边”的。
这些说法都是错误的！

来看下面这一张二维平面的求导三角型图。类比到损失函数和梯度概念上，图中的抛物线就是损失函数J(θ)，A(θ_a,J(θ_a))就是小球最初在的位置，B(θ_b,J(θ_b))就是一次滚动后小球移动到的位置。从A到B的方向就是梯度向量的反方向，指向损失函数在A点下降最快的方向。而梯度向量的大小是点A在图像上对θ求导后的结果，也是点A切线方向的斜率，橙色角的tan结果，记作d。

梯度下降每走一步，损失函数减小的量，是损失函数在θ变化之后的取值的变化，写作J(θ_b)-J(θ_a)，这是二维平面的求导三角型中的“对边”。
梯度下降每走一步，参数向量的变化，写作θ_b-θ_a，根据参数向量的迭代公式，就是步长 * 梯度向量的大小，记作α*d，这是二维平面的求倒三角形中的“邻边”。
梯度下降中每走一步，下降的距离，是，是对边和邻边的根号下平方和，是二维平面的求导三角型中的”斜边“。
所以，步长不是任何物理距离，它甚至不是梯度下降过程中任何距离的直接变化，它是梯度向量的大小上的一个比例，影响着参数向量每次迭代后改变的部分。

不难发现，既然参数迭代是靠梯度向量的大小d*步长α来实现的，而J(θ)的降低又是靠调节θ来实现的，所以步长可以调节损失函数下降的速率。在损失函数降低的方向上，步长越长，θ的变动就越大。相对的，步长如果很短，θ的每次变动就很小。具体地说，如果步长太大，损失函数下降得就非常快，需要的迭代次数就很少，但梯度下降过程可能跳过损失函数的最低点，无法获取最优值。而步长太小，虽然函数会逐渐逼近需要的最低点，但迭代的速度却很缓慢，迭代次数就需要很多。

在看小球运动时注意到，小球在进入深蓝色区域后，并没有直接找到某个点，而是在深蓝色区域中来回震荡了数次才停下，这种”震荡“其实就是因为设置的步长太大的缘故。但是在开始梯度下降之前，并不知道什么样的步长才合适，但梯度下降一定要在某个时候停止才可以，否则模型可能会无限地迭代下去。因此，在sklearn当中，设置参数max_iter最大迭代次数来代替步长，帮助控制模型的迭代速度并适时地让模型停下。max_iter越大，代表步长越小，模型迭代时间越长，反之，则代表步长设置很大，模型迭代时间很短。

迭代结束，获取到J(θ)的最小值后，就可以找出这个最小值对应的参数向量θ，逻辑回归的预测函数也就可以根据这个参数向量θ来建立了。

来看看乳腺癌数据集下，max_iter的学习曲线：

from sklearn.linear_model import LogisticRegression as LR
from sklearn.datasets import load_breast_cancer
import numpy as np
import matplotlib.pyplot as plt
from sklearn.model_selection import cross_val_score
from sklearn.feature_selection import SelectFromModel
from sklearn.model_selection import train_test_split
from sklearn.metrics import accuracy_score

data = load_breast_cancer()
X = data.data
y = data.target
l2 = []
l2test = []
Xtrain, Xtest, Ytrain, Ytest = train_test_split(X,y,test_size=0.3,random_state=420)
for i in np.arange(1,201,10):
    lrl2 = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=i)
    lrl2 = lrl2.fit(Xtrain,Ytrain)
    l2.append(accuracy_score(lrl2.predict(Xtrain),Ytrain))
    l2test.append(accuracy_score(lrl2.predict(Xtest),Ytest))
graph = [l2,l2test]
color = ["black","gray"]
label = ["L2","L2test"]
plt.figure(figsize=(20,5))
for i in range(len(graph)):
    plt.plot(np.arange(1,201,10),graph[i],color[i],label=label[i])
plt.legend(loc=4)
plt.xticks(np.arange(1,201,10))
plt.show()
#可以使用属性.n_iter_来调用本次求解中真正实现的迭代次数
lr = LR(penalty="l2",solver="liblinear",C=0.9,max_iter=300).fit(Xtrain,Ytrain)
print(lr.n_iter_)

当max_iter中限制的步数已经走完了，逻辑回归却还没有找到损失函数的最小值，参数的值还没有被收敛，sklearn就会弹出这样的红色警告：
当参数solver=“liblinear”：
当参数solver=“sag”：
虽然写法看起来略有不同，但其实都是一个含义，这是提醒：参数没有收敛，请增大max_iter中输入的数字。但不一定要听sklearn的。max_iter很大，意味着步长小，模型运行得会更加缓慢。虽然在梯度下降中追求的是损失函数的最小值，但这也可能意味着模型会过拟合（在训练集上表现得太好，在测试集上却不一定），因此，如果在max_iter报红条的情况下，模型的训练和预测效果都已经不错了，那就不需要再增大max_iter中的数目了，毕竟一切都以模型的预测效果为基准——只要最终的预测效果好，运行又快，那就一切都好，无所谓是否报红色警告了。
4.二元回归与多元回归：重要参数solver & multi_class
之前对逻辑回归的讨论，都是针对二分类的逻辑回归展开，其实sklearn提供了多种可以使用逻辑回归处理多分类问题的选项。比如说，可以把某种分类类型都看作1，其余的分类类型都为0值，和”数据预处理“中的二值化的思维类似，这种方法被称为"一对多"(One-vs-rest)，简称OvR，在sklearn中表示为“ovr"。又或者，可以把好几个分类类型划为1，剩下的几个分类类型划为0值，这是一种”多对多“(Many-vs-Many)的方法，简称MvM，在sklearn中表示为"Multinominal"。每种方式都配合L1或L2正则项来使用。

在sklearn中，使用参数multi_class来告诉模型，的预测标签是什么样的类型。
multi_class
输入"ovr", “multinomial”, “auto"来告知模型，要处理的分类问题的类型。默认是"ovr”。
‘ovr’:表示分类问题是二分类，或让模型使用"一对多"的形式来处理多分类问题。
‘multinomial’：表示处理多分类问题，这种输入在参数solver是’liblinear’时不可用。('liblinear’主要处理二分类问题）
“auto”：表示会根据数据的分类情况和其他参数来确定模型要处理的分类问题的类型。比如说，如果数据是二分类，或者solver的取值为"liblinear"，“auto"会默认选择"ovr”。反之，则会选择"nultinomial"。
注意：默认值将在0.22版本中从"ovr"更改为"auto"。

之前提到的梯度下降法，只是求解逻辑回归参数的一种方法，并且只讲解了求解二分类变量的参数时的各种原理。sklearn提供了多种选择，可以使用不同的求解器来计算逻辑回归。求解器的选择，由参数"solver"控制，共有五种选择。其中“liblinear”是二分类专用，也是现在的默认求解器。
(灰色色块为缺点)

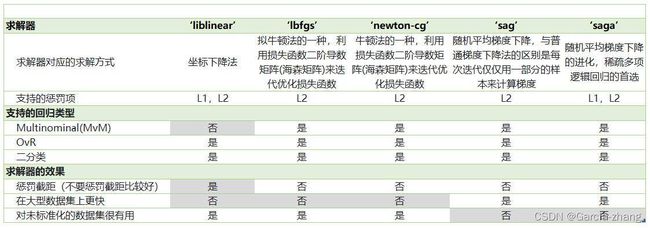
看看鸢尾花数据集上，multinomial和ovr的区别怎么样：

from sklearn.datasets import load_iris
from sklearn.linear_model import LogisticRegression
iris = load_iris()
for multi_class in ('multinomial', 'ovr'):
    clf = LogisticRegression(solver='sag', max_iter=100, random_state=42,multi_class=multi_class).fit(iris.data, iris.target)
#打印两种multi_class模式下的训练分数
#%的用法，用%来代替打印的字符串中，想由变量替换的部分。%.3f表示，保留三位小数的浮点数。%s表示，字符串。
#字符串后的%后使用元祖来容纳变量，字符串中有几个%，元祖中就需要有几个变量
    print("training score : %.3f (%s)" % (clf.score(iris.data, iris.target),multi_class))

5.样本不平衡与参数class_weight
样本不平衡是指在一组数据集中，标签的一类天生占有很大的比例，或误分类的代价很高，即想要捕捉出某种特定的分类的时候的状况。

什么情况下误分类的代价很高？例如，现在要对潜在犯罪者和普通人进行分类，如果没有能够识别出潜在犯罪者，那么这些人就可能去危害社会，造成犯罪，识别失败的代价会非常高，但如果，将普通人错误地识别成了潜在犯罪者，代价却相对较小。所以宁愿将普通人分类为潜在犯罪者后再人工甄别，但是却不愿将潜在犯罪者分类为普通人，有种"宁愿错杀不能放过"的感觉。

再比如说，在银行要判断“一个新客户是否会违约”，通常不违约的人vs违约的人会是99：1的比例，真正违约的人其实是非常少的。这种分类状况下，即便模型什么也不做，全把所有人都当成不会违约的人，正确率也能有99%，这使得模型评估指标变得毫无意义，根本无法达到“要识别出会违约的人”的建模目的。

因此要使用参数class_weight对样本标签进行一定的均衡，给少量的标签更多的权重，让模型更偏向少数类，向捕获少数类的方向建模。该参数默认None，此模式表示自动给与数据集中的所有标签相同的权重，即自动1：1。当误分类的代价很高的时候，使用”balanced“模式，只是希望对标签进行均衡的时候，什么都不填就可以解决样本不均衡问题。

但是，sklearn当中的参数class_weight变幻莫测，很难去找出这个参数引导的模型趋势，或者画出学习曲线来评估参数的效果，因此可以说是非常难用。
有着处理样本不均衡的各种方法，其中主流的是采样法，是通过重复样本的方式来平衡标签，可以进行上采样（增加少数类的样本），比如SMOTE，或者下采样（减少多数类的样本）。对于逻辑回归来说，上采样是最好的办法。将在案例中详细来讲如何在逻辑回归中使用上采样。

三、案例：用逻辑回归制作评分卡

在银行借贷场景中，评分卡是一种以分数形式来衡量一个客户的信用风险大小的手段，它衡量向别人借钱的人（受信人，需要融资的公司）不能如期履行合同中的还本付息责任，并让借钱给别人的人（授信人，银行等金融机构）造成经济损失的可能性。一般来说，评分卡打出的分数越高，客户的信用越好，风险越小。

这些”借钱的人“，可能是个人，有可能是有需求的公司和企业。对于企业来说，按照融资主体的融资用途，分别使用企业融资模型，现金流融资模型，项目融资模型等模型。而对于个人来说，有”四张卡“来评判个人的信用程度：A卡，B卡，C卡和F卡。而众人常说的“评分卡”其实是指A卡，又称为申请者评级模型，主要应用于相关融资类业务中新用户的主体评级，即判断金融机构是否应该借钱给一个新用户，如果这个人的风险太高，可以拒绝贷款。

一个完整的模型开发，需要有以下流程：

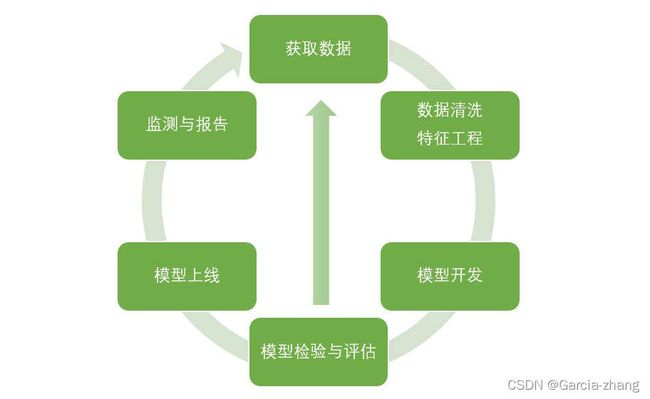
以个人消费类贷款数据，介绍A卡的建模和制作流程，核心会在”数据清洗“和“模型开发”上。模型检验与评估也非常重要，但内容太多，就不再赘述了。
3.1 导库，获取数据

import numpy as np
import pandas as pd
from sklearn.linear_model import LogisticRegression as LR
#其实日常在导库的时候，并不是一次性能够知道我们要用的所有库的。通常都是在建模过程中逐渐导入需要的库。
data = pd.read_csv(r"D:\data\datasets\rankingcard.csv",index_col=0)

在银行系统中，这个数据通常来自于其他部门的同事的收集，因此千万别忘记问问给数据的人各个项都是什么含义。通常来说，当特征非常多的时候（比如几百个），都会有一个附带的excel或pdf文档给到你，备注了各个特征都是什么含义。这种情况下其实要一个个去看还是非常困难，所以如果特征很多，建议先做降维，具体参考“2.2.2 逻辑回归中的特征工程”。
3.2 探索数据与数据预处理

#观察数据类型
print(data.head())
#观察数据结构
print(data.shape)
print(data.info())

这一步要看样本总体的大概情况，比如查看缺失值，量纲是否统一，是否需要做哑变量等等。其实数据的探索和数据的预处理并不是完全分开的，并不一定非要先做哪一个，因此这个顺序只是供大家参考。

特征/标签	含义
SeriousDlqin2yrs	出现 90 天或更长时间的逾期行为（即定义好坏客户）
RevolvingUtilizationOfUnsecuredLines	贷款以及信用卡可用额度与总额度比例
age	借款人借款年龄
NumberOfTime30-59DaysPastDueNotWorse	过去两年内出现35-59天逾期但是没有发展得更坏的次数
DebtRatio	每月偿还债务，赡养费，生活费用除以月总收入
MonthlyIncome	月收入
NumberOfOpenCreditLinesAndLoans	开放式贷款和信贷数量
NumberOfTimes90DaysLate	过去两年内出现90天逾期或更坏的次数
NumberRealEstateLoansOrLines	抵押贷款和房地产贷款数量，包括房屋净值信贷额度
NumberOfTime60-89DaysPastDueNotWorse	过去两年内出现60-89天逾期但是没有发展得更坏的次数
NumberOfDependents	家庭中不包括自身的家属人数（配偶，子女等）

3.2.1 去除重复值
现实数据，尤其是银行业数据，可能会存在的一个问题就是样本重复，即有超过一行的样本所显示的所有特征都一样。有时候可能时人为输入重复，有时候可能是系统录入重复，总而言之必须对数据进行去重处理。可能有人会说，难道不可能出现说两个样本的特征就是一模一样，但他们是两个样本吗？比如，两个人，一模一样的名字，年龄，性别，学历，工资……当特征量很少的时候，这的确是有可能的，但一些指标，比如说家属人数，月收入，已借有的房地产贷款数量等等，几乎不可能都出现一样。尤其是银行业数据经常是几百个特征，所有特征都一样的可能性是微乎其微的。即便真的出现了如此极端的情况，也可以当作是少量信息损失，将这条记录当作重复值除去。

#去除重复值
data.drop_duplicates(inplace=True)
print(data.info())
#删除之后千万不要忘记，恢复索引
data.index = range(data.shape[0])
print(data.info())

3.2.2 填补缺失值

#探索缺失值
print(data.info())
print(data.isnull().sum()/data.shape[0])#空值的比例
#print(data.isnull().mean())

第二个要面临的问题，就是缺失值。这里需要填补的特征是“收入”和“家属人数”。“家属人数”缺失很少，仅缺失了大约2.5%，可以考虑直接删除，或者使用均值来填补。“收入”缺失了几乎20%，并且“收入”必然是一个对信用评分来说很重要的因素，因此这个特征必须要进行填补。
在这里，使用均值填补“家属人数”。

data["NumberOfDependents"].fillna(int(data["NumberOfDependents"].mean()),inplace=True)
#如果你选择的是删除那些缺失了2.5%的特征，千万记得恢复索引哟~
print(data.info())
print(data.isnull().sum()/data.shape[0])

那字段"收入"怎么办呢？对于银行数据来说，甚至可以有这样的推断：一个来借钱的人应该是会知道，“高收入”或者“稳定收入”于他/她自己而言会是申请贷款过程中的一个助力，因此如果收入稳定良好的人，肯定会倾向于写上自己的收入情况，那么这些“收入”栏缺失的人，更可能是收入状况不稳定或收入比较低的人。基于这种判断，可以用比如说，四分位数来填补缺失值，把所有收入为空的客户都当成是低收入人群。当然了，也有可能这些缺失是银行数据收集过程中的失误，并无法判断为什么收入栏会有缺失，所以推断也有可能是不正确的。具体采用什么样的手段填补缺失值，要和业务人员去沟通，观察缺失值是如何产生的。在这里，使用随机森林填补“收入”。

随机森林利用“既然可以使用A，B，C去预测Z，那也可以使用A，C，Z去预测B”的思想来填补缺失值。对于一个有n个特征的数据来说，其中特征T有缺失值，就把特征T当作标签，其他的n-1个特征和原本的标签组成新的特征矩阵。那对于T来说，它没有缺失的部分，就是Y_train，这部分数据既有标签也有特征，而它缺失的部分，只有特征没有标签，就是需要预测的部分。

特征T不缺失的值对应的其他n-1个特征 + 本来的标签：X_train 特征T不缺失的值：Y_train 特征T缺失的值对应的其
他n-1个特征 + 本来的标签：X_test 特征T缺失的值：未知，需要预测的Y_test

这种做法，对于某一个特征大量缺失，其他特征却很完整的情况，非常适用。

之前所做的随机森林填补缺失值的案例中，面临整个数据集中多个特征都有缺失的情况，因此要先对特征排序，遍历所有特征来进行填补。这次只需要填补“收入”一个特征，就无需循环那么麻烦了，可以直接对这一列进行填补。

#先写一个能够填补任何列的函数：
def fill_missing_rf(X,y,to_fill):
    """
    使用随机森林填补一个特征的缺失值的函数
    参数：
    X：要填补的特征矩阵
    y：完整的，没有缺失值的标签
    to_fill：字符串，要填补的那一列的名称
    """
    
    #构建新特征矩阵和新标签
    df = X.copy()
    fill = df.loc[:,to_fill]
    df = pd.concat([df.loc[:,df.columns != to_fill],pd.DataFrame(y)],axis=1)
    
    #找出我们的训练集和测试集
    Ytrain = fill[fill.notnull()]
    Ytest = fill[fill.isnull()]
    Xtrain = df.iloc[Ytrain.index,:]
    Xtest = df.iloc[Ytest.index,:]
    
    #用随机森林回归来填补缺失值
    from sklearn.ensemble import RandomForestRegressor as rfr
    rfr = rfr(n_estimators=100)
    rfr = rfr.fit(Xtrain, Ytrain)
    Ypredict = rfr.predict(Xtest)
    
    return Ypredict
#接着创造函数需要的参数，将参数导入函数，产出结果：
X = data.iloc[:,1:]
y = data["SeriousDlqin2yrs"]#y=data.iloc[:,0]
X.shape

#=====【TIME WARNING：1 min】=====#
y_pred = fill_missing_rf(X,y,"MonthlyIncome")

#确认结果合理之后，我们就可以将数据覆盖了
data.loc[data.loc[:,"MonthlyIncome"].isnull(),"MonthlyIncome"] = y_pred

3.2.3 描述性统计处理异常值
现实数据永远都会有一些异常值，首先要去把他们捕捉出来，然后观察他们的性质。注意，并不是要排除掉所有异常值，相反很多时候，异常值是重点研究对象，比如说，双十一中购买量超高的品牌，或课堂上让很多学生都兴奋的课题，这些是要重点研究观察的。

日常处理异常值，使用箱线图或者3σ法则来找到异常值（千万不要说依赖于眼睛看,除了业务理解，还要有方法）。但在银行数据中，希望排除的“异常值”不是一些超高或超低的数字，而是一些不符合常理的数据：比如，收入不能为负数，但是一个超高水平的收入却是合理的，可以存在的。所以在银行业中，往往就使用普通的描述性统计来观察数据的异常与否与数据的分布情况。注意，这种方法只能在特征量有限的情况下进行，如果有几百个特征又无法成功降维或特征选择不管用，那还是用3σ比较好。

#描述性统计
data.describe([0.01,0.1,0.25,.5,.75,.9,.99]).T

#异常值被观察到，年龄的最小值居然有0，这不符合银行的业务需求，即便是儿童账户也要至少8岁，可以查看一下年龄为0的人有多少
print((data["age"] == 0).sum())
#发现只有一个人年龄为0，可以判断这肯定是录入失误造成的，可以当成是缺失值来处理，直接删除掉这个样本
data = data[data["age"] != 0]

"""
另外，有三个指标看起来很奇怪：
"NumberOfTime30-59DaysPastDueNotWorse"、"NumberOfTime60-89DaysPastDueNotWorse"、"NumberOfTimes90DaysLate"
这三个指标分别是“过去两年内出现35-59天逾期但是没有发展的更坏的次数”，“过去两年内出现60-89天逾期但是没有发展的更坏的次数”,“过去两年内出现90天逾期的次数”。
这三个指标，在99%的分布的时候依然是2，最大值却是98，看起来非常奇怪。一个人在过去两年内逾期35~59天98次，一年6个60天，两年内逾期98次这是怎么算出来的？
可以去咨询业务人员，请教这个逾期次数是如何计算的。如果这个指标是正常的，那这些两年内逾期了98次的客户，应该都是坏客户。在无法询问他们情况下，查看一下有多少个样本存在这种异常：
"""
print(data[data.loc[:,"NumberOfTimes90DaysLate"] > 90].count())
#有225个样本存在这样的情况，并且这些样本标签并不都是1，他们并不都是坏客户。因此基本可以判断，这些样本是某种异常，应该把它们删除。
data = data[data.loc[:,"NumberOfTimes90DaysLate"] < 90]

#恢复索引
data.index = range(data.shape[0])
print(data.info())

3.2.4 为什么不统一量纲，也不标准化数据分布？
在描述性统计结果中，可以观察到数据量纲明显不统一，而且存在一部分极偏的分布，虽然逻辑回归对于数据没有分布要求，但是知道如果数据服从正态分布的话梯度下降可以收敛得更快。但在这里，不对数据进行标准化处理，也不进行量纲统一，为什么？

无论算法有什么样的规定，无论统计学中有什么样的要求，最终目的都是要为业务服务。现在要制作评分卡，评分卡是要给业务人员们使用的基于新客户填写的各种信息为客户打分的一张卡片，而为了制作这张卡片，需要对数据进行一个“分档”，比如说，年龄20～30岁为一档，年龄30～50岁为一档，月收入1W以上为一档，5000~1W为一档，每档的分数不同。

一旦将数据统一量纲，或者标准化了之后，数据大小和范围都会改变，统计结果是漂亮了，但是对于业务人员来说，他们完全无法理解，标准化后的年龄在0.00328～0.00467之间为一档是什么含义。并且，新客户填写的信息，天生就是量纲不统一的，的确可以将所有的信息录入之后，统一进行标准化，然后导入算法计算，但是最终落到业务人员手上去判断的时候，他们会完全不理解为什么录入的信息变成了一串统计上很美但实际上根本看不懂的数字。由于业务要求，在制作评分卡的时候，要尽量保持数据的原貌，年龄就是8～110的数字，收入就是大于0，最大值可以无限的数字，即便量纲不统一，也不对数据进行标准化处理。
3.2.5 样本不均衡问题

#探索标签的分布
X = data.iloc[:,1:]
y = data.iloc[:,0]
print(y.value_counts())
n_sample = X.shape[0]
n_1_sample = y.value_counts()[1]
n_0_sample = y.value_counts()[0]
print('样本个数：{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample,n_1_sample/n_sample,n_0_sample/n_sample))

可以看出，样本严重不均衡。虽然大家都在努力防范信用风险，但实际违约的人并不多。并且，银行并不会真的一棒子打死所有会违约的人，很多人是会还钱的，只是忘记了还款日，很多人是不愿意欠人钱的，但是当时真的很困难，资金周转不过来，所以发生逾期，但一旦他有了钱，他就会把钱还上。对于银行来说，只要最后能够把钱还上，我都愿意借钱给你，因为我借给你就有收入（利息）。所以，对于银行来说，真正想要被判别出来的其实是”恶意违约“的人，而这部分人数非常非常少，样本就会不均衡。这一直是银行业建模的一个痛点：永远希望捕捉少数类。

之前提到过，逻辑回归中使用最多的是上采样方法来平衡样本。

#如果报错，就在prompt安装：pip install imblearn
import imblearn
#imblearn是专门用来处理不平衡数据集的库，在处理样本不均衡问题中性能高过sklearn很多
#imblearn里面也是一个个的类，也需要进行实例化，fit拟合，和sklearn用法相似
from imblearn.over_sampling import SMOTE

sm = SMOTE(random_state=42) #实例化
X,y = sm.fit_resample(X,y)#返回已经上采样完毕过后的特征矩阵和标签
n_sample_ = X.shape[0]
pd.Series(y).value_counts()
n_1_sample = pd.Series(y).value_counts()[1]
n_0_sample = pd.Series(y).value_counts()[0]
print('样本个数：{}; 1占{:.2%}; 0占{:.2%}'.format(n_sample_,n_1_sample/n_sample_,n_0_sample/n_sample_))

如此就实现了样本平衡，样本量也增加了。
3.2.6 分训练集和测试集

from sklearn.model_selection import train_test_split
X = pd.DataFrame(X)
y = pd.DataFrame(y)

X_train, X_vali, Y_train, Y_vali = train_test_split(X,y,test_size=0.3,random_state=420)
model_data = pd.concat([Y_train, X_train], axis=1)
model_data.index = range(model_data.shape[0])
model_data.columns = data.columns

vali_data = pd.concat([Y_vali, X_vali], axis=1)
vali_data.index = range(vali_data.shape[0])
vali_data.columns = data.columns

model_data.to_csv(r"D:\data\datasets\model_data.csv")
vali_data.to_csv(r"D:\data\datasets\vali_data.csv")

3.3 分箱
前面提到过，要制作评分卡，是要给各个特征进行分档，以便业务人员能够根据新客户填写的信息为客户打分。因此在评分卡制作过程中，一个重要的步骤就是分箱。可以说，分箱是评分卡最难，也是最核心的思路，分箱的本质，其实就是离散化连续变量，好让拥有不同属性的人被分成不同的类别（打上不同的分数），其实本质比较类似于聚类。在分箱中要回答几个问题：

首先，要分多少个箱子才合适？

最开始并不知道，但是既然是将连续型变量离散化，想也知道箱子个数必然不能太多，最好控制在十个以下。而用来制作评分卡，最好能在4~5个为最佳。离散化连续变量必然伴随着信息的损失，并且箱子越少，信息损失越大。为了衡量特征上的信息量以及特征对预测函数的贡献，银行业定义了概念Information value(IV)：

其中N是这个特征上箱子的个数，i代表每个箱子，good%是这个箱内的优质客户（标签为0的客户）占整个特征中所有优质客户的比例，bad%是这个箱子里的坏客户（就是那些会违约，标签为1的那些客户）占整个特征中所有坏客户的比例，而WOE_i则写作：

这是银行业中用来衡量违约概率的指标，中文叫做证据权重(weight of Evidence)，本质其实就是优质客户比上坏客户的比例的对数。WOE是对一个箱子来说的，WOE越大，代表了这个箱子里的优质客户越多。而IV是对整个特征来说的，IV代表的意义是我们特征上的信息量以及这个特征对模型的贡献，由下表来控制：

IV	特征对预测函数的贡献
< 0.03	特征几乎不带有效信息，对模型没有贡献，这种特征可以被删除
0.03 ~ 0.09	有效信息很少，对模型的贡献度低
0.1 ~ 0.29	有效信息一般，对模型的贡献度中等
0.3 ~ 0.49	有效信息较多，对模型的贡献度较高
>=0.5	有效信息非常多，对模型的贡献超高并且可疑

可见，IV并非越大越好，想要找到IV的大小和箱子个数的平衡点。箱子越多，IV必然越小，因为信息损失会非常多，所以，会对特征进行分箱，然后计算每个特征在每个箱子数目下的WOE值，利用IV值的曲线，找出合适的分箱个数。

其次，分箱要达成什么样的效果？

分箱的目的是希望不同属性的人有不同的分数，因此希望在同一个箱子内的人的属性是尽量相似的，而不同箱子的人的属性是尽量不同的，即业界常说的”组间差异大，组内差异小“。对于评分卡来说，就是说希望一个箱子内的人违约概率是类似的，而不同箱子的人的违约概率差距很大，即WOE差距要大，并且每个箱子中坏客户所占的比重（bad%）也要不同。那可以使用卡方检验来对比两个箱子之间的相似性，如果两个箱子之间卡方检验的P值很大，则说明他们非常相似，就可以将这两个箱子合并为一个箱子。

基于这样的思想，总结出对一个特征进行分箱的步骤：
1）首先把连续型变量分成一组数量较多的分类型变量，比如，将几万个样本分成100组，或50组
2）确保每一组中都要包含两种类别的样本，否则IV值会无法计算
3）对相邻的组进行卡方检验，卡方检验的P值很大的组进行合并，直到数据中的组数小于设定的N箱为止
4）让一个特征分别分成[2,3,4…20]箱，观察每个分箱个数下的IV值如何变化，找出最适合的分箱个数
5）分箱完毕后，计算每个箱的WOE值， ，观察分箱效果
这些步骤都完成后，可以对各个特征都进行分箱，然后观察每个特征的IV值，以此来挑选特征。

接下来就以"age"为例子，来看看分箱如何完成。
3.3.1 等频分箱

#按照等频对需要分箱的列进行分箱
#datafram["列名"]#当这个列存在的时候，就是该列的索引；
#当这个列名不存在的时候，dataframe会自动生成叫做这个列名的一个新的列
model_data["qcut"], updown = pd.qcut(model_data["age"], retbins=True, q=20)
#model_data["qcut"]生成一个叫qcut的新列
#updown指箱子的上限和下限
"""
pd.qcut，基于分位数的分箱函数，本质是将连续型变量离散化
只能够处理一维数据。返回箱子的上限和下限
参数q：要分箱的个数
参数retbins=True来要求同时返回结构为:索引为样本索引，元素为分到的箱子的Series
现在返回两个值：每个样本属于哪个箱子，以及所有箱子的上限和下限
"""

#让model_data新添加一列叫做“分箱”，这一列其实就是每个样本所对应的箱子
print(model_data["qcut"])
#所有箱子的上限和下限
print(updown)

# 统计每个分箱中0和1的数量
# 这里使用了数据透视表的功能groupby
#.groupby(by="qcut").count()表示按qcut聚合计算个数
coount_y0 = model_data[model_data["SeriousDlqin2yrs"] == 0].groupby(by="qcut").count()["SeriousDlqin2yrs"]
coount_y1 = model_data[model_data["SeriousDlqin2yrs"] == 1].groupby(by="qcut").count()["SeriousDlqin2yrs"]

#num_bins值分别为每个区间的上界，下界，0出现的次数，1出现的次数
num_bins = [*zip(updown,updown[1:],coount_y0,coount_y1)]
#updown,updown[1:]这样会把上一个元组的下限作为下一个元组的上限
#注意zip会按照最短列来进行结合
#[*zip([1,2,3],["a","b","c","d"])]
print(num_bins)

3.3.2【选学】 确保每个箱中都有0和1

for i in range(20):
    #如果第一个组没有包含正样本或负样本，向后合并
    if 0 in num_bins[0][2:]:
        num_bins[0:2] = [(num_bins[0][0],num_bins[1][1],num_bins[0][2]+num_bins[1][2],num_bins[0][3]+num_bins[1][3])]
    continue
    """
    合并了之后，第一行的组也不一定有两种样本
    （如果原本的第一组和第二组都没有包含正样本或者负样本，那即便合并之后，第一行的组也还是没有包含）
    所以每次合并完毕之后，还需要再检查，第一组是否已经包含了两种样本
    这里使用continue跳出了本次循环，开始下一次循环，所以回到了最开始的for i in range(20), 让i+1
    这就跳过了下面的代码，又从头开始检查，第一组是否包含了两种样本
    
    如果第一组中依然没有包含两种样本，则if通过，继续合并，每合并一次就会循环检查一次，最多合并20次
    如果第一组中已经包含两种样本，则if不通过，就开始执行下面的代码
    """
    #已经确认第一组中肯定包含两种样本了，如果其他组没有包含两种样本，就向前合并
    
    #此时的num_bins已经被上面的代码处理过，可能被合并过，也可能没有被合并
    #但无论如何，都要在num_bins中遍历，所以写成in range(len(num_bins))
    for i in range(len(num_bins)):
        if 0 in num_bins[i][2:]:
            num_bins[i-1:i+1] = [(num_bins[i-1][0],num_bins[i][1],num_bins[i-1][2]+num_bins[i][2],num_bins[i-1][3]+num_bins[i][3])]
            break
        #如果对第一组和对后面所有组的判断中，都没有进入if去合并，则提前结束所有的循环
        else:
            break
        """
        这个break，只有在if被满足的条件下才会被触发，即只有发生了合并，才会打断for i in range(len(num_bins))这个循环
        因为是在range(len(num_bins))中遍历，但合并发生后，len(num_bins)发生了改变，但循环却不会重新开始
        举个例子，本来num_bins是5组，for i in range(len(num_bins))在第一次运行的时候就等于for i in range(5)
        range中输入的变量会被转换为数字，不会跟着num_bins的变化而变化，所以i会永远在[0,1,2,3,4]中遍历
        进行合并后，num_bins变成了4组，已经不存在=4的索引了，但i却依然会取到4，循环就会报错
        因此在这里，一旦if被触发，即一旦合并发生，就让循环被破坏，使用break跳出当前循环
        循环就会回到最开始的for i in range(20)中
        此时判断第一组是否有两种标签的代码不会被触发，但for i in range(len(num_bins))却会被重新运行
        这样就更新了i的取值，循环就不会报错了
        """

3.3.3 定义WOE和IV函数

#计算WOE和BAD RATE

def get_woe(num_bins):
    # 通过 num_bins 数据计算 woe
    columns = ["min","max","count_0","count_1"]
    df = pd.DataFrame(num_bins,columns=columns)
    df["total"] = df.count_0 + df.count_1#一个箱子中的所有样本数
    df["percentage"] = df.total / df.total.sum()#一个箱子里的样本数占所有样本数的比例
    df["bad_rate"] = df.count_1 / df.total#一个箱中的坏样本所占的比例 (bad/total)
    df["good%"] = df.count_0/df.count_0.sum()#一个箱中的好样本占整个特征中的好样本的比例
    df["bad%"] = df.count_1/df.count_1.sum()#一个箱中的坏样本占整个特征中的坏样本的比例
    df["woe"] = np.log(df["good%"] / df["bad%"])
    return df

#计算IV值
def get_iv(df):
    rate = df["good%"] - df["bad%"]
    iv = np.sum(rate * df.woe)
    return iv

3.3.4 卡方检验，合并箱体，画出IV曲线

num_bins_ = num_bins.copy()
#num_bins中最主要的差别就是0和1的数量的不同，卡方检验就是计算两个箱中0和1的个数的相似性
#让卡方值最大的两组数据合并
import matplotlib.pyplot as plt
import scipy

IV = []
axisx = []

while len(num_bins_) > 2:#while循环常用于不知道要循环多少次时使用
    pvs = []
    # 获取 num_bins_两两之间的卡方检验的置信度（或卡方值）
    for i in range(len(num_bins_)-1):
        x1 = num_bins_[i][2:]#取出第一个箱中的0和1的个数
        x2 = num_bins_[i+1][2:]#取出第二个箱中的0和1的个数
        # 0 返回 chi2 值，1 返回 p 值。
        pv = scipy.stats.chi2_contingency([x1,x2])[1]#计算两个箱中1的个数的卡方相似性（p值）
        # chi2 = scipy.stats.chi2_contingency([x1,x2])[0]
        pvs.append(pv)
    # 通过 p 值进行处理。合并 p 值最大的两组
    i = pvs.index(max(pvs))
    num_bins_[i:i+2] = [(num_bins_[i][0],num_bins_[i+1][1],num_bins_[i][2]+num_bins_[i+1][2],num_bins_[i][3]+num_bins_[i+1][3])]
    bins_df = get_woe(num_bins_)
    axisx.append(len(num_bins_))#合并后箱的个数
    IV.append(get_iv(bins_df))#合并后对应的IV值
plt.figure()
plt.plot(axisx,IV)
plt.xticks(axisx)
plt.xlabel("number of box")
plt.ylabel("IV")
plt.show()

3.3.5 用最佳分箱个数分箱，并验证分箱结果

#将合并箱体的部分定义为函数，并实现分箱：
def get_bin(num_bins_,n):
    while len(num_bins_) > n:
        pvs = []
        for i in range(len(num_bins_)-1):
            x1 = num_bins_[i][2:]
            x2 = num_bins_[i+1][2:]
            pv = scipy.stats.chi2_contingency([x1,x2])[1]
            # chi2 = scipy.stats.chi2_contingency([x1,x2])[0]
            pvs.append(pv)
        i = pvs.index(max(pvs))
        num_bins_[i:i+2] = [(num_bins_[i][0],num_bins_[i+1][1],num_bins_[i][2]+num_bins_[i+1][2],num_bins_[i][3]+num_bins_[i+1][3])]
    return num_bins_
afterbins = get_bin(num_bins,6)
print(afterbins)
bins_df = get_woe(afterbins)
print(bins_df)
#woe应该是单调变化的，要么由正到负，要么由负到正，或者只有一个转折点，如果出现两个以上的转折点说明分箱过程有问题

3.3.6 将选取最佳分箱个数的过程包装为函数

#为了最优分箱而画图
def graphforbestbin(DF, X, Y, n=5,q=20,graph=True):
    """
    自动最优分箱函数，基于卡方检验的分箱
    参数：
    DF: 需要输入的数据
    X: 需要分箱的列名
    Y: 分箱数据对应的标签 Y 列名
    n: 保留分箱个数
    q: 初始分箱的个数
    graph: 是否要画出IV图像#graph=True时画图
    区间为前开后闭 (]
    """
    DF = DF[[X,Y]].copy()
    DF["qcut"],bins = pd.qcut(DF[X], retbins=True, q=q,duplicates="drop")
    coount_y0 = DF.loc[DF[Y]==0].groupby(by="qcut").count()[Y]
    coount_y1 = DF.loc[DF[Y]==1].groupby(by="qcut").count()[Y]
    num_bins = [*zip(bins,bins[1:],coount_y0,coount_y1)]

    for i in range(q):
        if 0 in num_bins[0][2:]:
            num_bins[0:2] = [(num_bins[0][0],num_bins[1][1],num_bins[0][2]+num_bins[1][2],num_bins[0][3]+num_bins[1][3])]
            continue
        for i in range(len(num_bins)):
            if 0 in num_bins[i][2:]:
                num_bins[i-1:i+1] = [(num_bins[i-1][0],num_bins[i][1],num_bins[i-1][2]+num_bins[i][2],num_bins[i-1][3]+num_bins[i][3])]
                break
            else:
                break
    def get_woe(num_bins):
        columns = ["min","max","count_0","count_1"]
        df = pd.DataFrame(num_bins,columns=columns)
        df["total"] = df.count_0 + df.count_1
        df["percentage"] = df.total / df.total.sum()
        df["bad_rate"] = df.count_1 / df.total
        df["good%"] = df.count_0/df.count_0.sum()
        df["bad%"] = df.count_1/df.count_1.sum()
        df["woe"] = np.log(df["good%"] / df["bad%"])
        return df
    def get_iv(df):
        rate = df["good%"] - df["bad%"]
        iv = np.sum(rate * df.woe)
        return iv
    IV = []
    axisx = []
    while len(num_bins) > n:
        pvs = []
        for i in range(len(num_bins)-1):
            x1 = num_bins[i][2:]
            x2 = num_bins[i+1][2:]
            pv = scipy.stats.chi2_contingency([x1,x2])[1]
            pvs.append(pv)
            i = pvs.index(max(pvs))
            num_bins[i:i+2] = [(num_bins[i][0],num_bins[i+1][1],num_bins[i][2]+num_bins[i+1][2],num_bins[i][3]+num_bins[i+1][3])]
            bins_df = pd.DataFrame(get_woe(num_bins))
            axisx.append(len(num_bins))
            IV.append(get_iv(bins_df))
    if graph:
        plt.figure()
        plt.plot(axisx,IV)
        plt.xticks(axisx)
        plt.xlabel("number of box")
        plt.ylabel("IV")
        plt.show()
    return bins_df

3.3.7 对所有特征进行分箱选择

print(model_data.columns)
for i in model_data.columns[1:-1]: 
    print(i)
    graphforbestbin(model_data,i,"SeriousDlqin2yrs",n=2,q=20)

可以发现，不是所有的特征都可以使用这个分箱函数，比如说像家人数量，就无法分出20组。于是将可以分箱的特征放出来单独分组，不能自动分箱的变量自己观察然后手写：

auto_col_bins = {"RevolvingUtilizationOfUnsecuredLines":6,
                 "age":5,
                 "DebtRatio":4,
                 "MonthlyIncome":3,
                 "NumberOfOpenCreditLinesAndLoans":5}

#不能使用自动分箱的变量
hand_bins = {"NumberOfTime30-59DaysPastDueNotWorse":[0,1,2,13]
             ,"NumberOfTimes90DaysLate":[0,1,2,17]
             ,"NumberRealEstateLoansOrLines":[0,1,2,4,54]
             ,"NumberOfTime60-89DaysPastDueNotWorse":[0,1,2,8]
             ,"NumberOfDependents":[0,1,2,3]}

#保证区间覆盖使用 np.inf替换最大值，用-np.inf替换最小值
hand_bins = {k:[-np.inf,*v[:-1],np.inf] for k,v in hand_bins.items()}

#接下来对所有特征按照选择的箱体个数和手写的分箱范围进行分箱：
bins_of_col = {}
# 生成自动分箱的分箱区间和分箱后的 IV 值
for col in auto_col_bins:
    bins_df = graphforbestbin(model_data
                              ,col
                              ,"SeriousDlqin2yrs"
                              ,n=auto_col_bins[col]#使用字典的性质来取出每个特征所对应的箱的数量
                              ,q=20
                              ,graph=False)
    bins_list = sorted(set(bins_df["min"]).union(bins_df["max"]))
    #保证区间覆盖使用 np.inf 替换最大值 -np.inf 替换最小值
    bins_list[0],bins_list[-1] = -np.inf,np.inf
    bins_of_col[col] = bins_list
#合并手动分箱数据
bins_of_col.update(hand_bins)
print(bins_of_col)

3.4 计算各箱的WOE并映射到数据中
现在已经有了箱子，接下来要做的是计算各箱的WOE，并且把WOE替换到原始数据model_data中，因为将使用WOE覆盖后的数据来建模，希望获取的是”各个箱”的分类结果，即评分卡上各个评分项目的分类结果。

data = model_data.copy()
#函数pd.cut，可以根据已知的分箱间隔把数据分箱
#参数为 pd.cut(数据，以列表表示的分箱间隔)
data = data[["age","SeriousDlqin2yrs"]].copy()
data["cut"] = pd.cut(data["age"],[-np.inf, 48.49986200790144, 58.757170160044694, 64.0,74.0, np.inf])
print(data)
#将数据按分箱结果聚合，并取出其中的标签值
data.groupby("cut")["SeriousDlqin2yrs"].value_counts()
#使用unstack()来将树状结构变成表状结构
data.groupby("cut")["SeriousDlqin2yrs"].value_counts().unstack()
bins_df = data.groupby("cut")["SeriousDlqin2yrs"].value_counts().unstack()
bins_df["woe"] = np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))

#把以上过程包装成函数
def get_woe(df,col,y,bins):
    df = df[[col,y]].copy()
    df["cut"] = pd.cut(df[col],bins)
    bins_df = df.groupby("cut")[y].value_counts().unstack()
    woe = bins_df["woe"] =np.log((bins_df[0]/bins_df[0].sum())/(bins_df[1]/bins_df[1].sum()))
    return woe
#将所有特征的WOE存储到字典当中
woeall = {}
for col in bins_of_col:
    woeall[col] = get_woe(model_data,col,"SeriousDlqin2yrs",bins_of_col[col])
print(woeall)

#接下来，把所有WOE映射到原始数据中：
#不希望覆盖掉原本的数据，创建一个新的DataFrame，索引和原始数据model_data一模一样
model_woe = pd.DataFrame(index=model_data.index)
#将原数据分箱后，按箱的结果把WOE结构用map函数映射到数据中
model_woe["age"] = pd.cut(model_data["age"],bins_of_col["age"]).map(woeall["age"])
#对所有特征操作可以写成：
for col in bins_of_col:
    model_woe[col] = pd.cut(model_data[col],bins_of_col[col]).map(woeall[col])
#将标签补充到数据中
model_woe["SeriousDlqin2yrs"] = model_data["SeriousDlqin2yrs"]
#这就是我们的建模数据了
print(model_woe.head())

3.5 建模与模型验证
终于弄完了训练集，接下来要处理测试集，在已经有分箱的情况下，测试集的处理就非常简单了，只需要将已经计算好的WOE映射到测试集中去就可以了：

#处理测试集
vali_woe = pd.DataFrame(index=vali_data.index)
for col in bins_of_col:
    vali_woe[col] = pd.cut(vali_data[col],bins_of_col[col]).map(woeall[col])
vali_woe["SeriousDlqin2yrs"] = vali_data["SeriousDlqin2yrs"]
vali_X = vali_woe.iloc[:,:-1]
vali_y = vali_woe.iloc[:,-1]

X = model_woe.iloc[:,:-1]
y = model_woe.iloc[:,-1]
from sklearn.linear_model import LogisticRegression as LR
lr = LR().fit(X,y)
print(lr.score(vali_X,vali_y))

#返回的结果一般，可以试着使用C和max_iter的学习曲线把逻辑回归的效果调上去。
c_1 = np.linspace(0.01,1,20)
c_2 = np.linspace(0.01,0.2,20)
score = []
for i in c_2:
    lr = LR(solver='liblinear',C=i).fit(X,y)
    score.append(lr.score(vali_X,vali_y))
plt.figure()
plt.plot(c_2,score)
plt.show()
print(lr.n_)
score = []
for i in [1,2,3,4,5,6]:
    lr = LR(solver='liblinear',C=0.025,max_iter=i).fit(X,y)
    score.append(lr.score(vali_X,vali_y))
plt.figure()
plt.plot([1,2,3,4,5,6],score)
plt.show()
#尽管从准确率来看，模型效果属于一般，但可以来看看ROC曲线上的结果。
import scikitplot as skplt
#%%cmd
#pip install scikit-plot
vali_proba_df = pd.DataFrame(lr.predict_proba(vali_X))
skplt.metrics.plot_roc(vali_y, vali_proba_df,plot_micro=False,figsize=(6,6),plot_macro=False)

3.6 制作评分卡
建模完毕，使用准确率和ROC曲线验证了模型的预测能力。接下来就是要将逻辑回归转换为标准评分卡了。评分卡中的分数，由以下公式计算：

其中A与B是常数，A叫做“补偿”，B叫做“刻度”，log(odds)代表了一个人违约的可能性。其实逻辑回归的结果取对数几率形式会得到θ^Tx，即我们的参数*特征矩阵，所以log(odds)其实就是参数。两个常数可以通过两个假设的分值带入公式求出，这两个假设分别是：

1. 某个特定的违约概率下的预期分值
2. 指定的违约概率翻倍的分数（PDO）
   例如，假设对数几率为1/60时设定的特定分数为600，PDO=20，那么对数几率为1/30时的分数就是620。带入以上性表达式，可以得到：
   
   用numpy可以很容易求出A和B的值：

B = 20/np.log(2)
A = 600 + B*np.log(1/60)
print(B,A)

有了A和B，分数就很容易得到了。其中不受评分卡中各特征影响的基础分，就是将截距作为log(odds)带入公式进行计算，而其他各个特征各个分档的分数，也是将系数带入进行计算：

base_score = A - B*lr.intercept_
print(base_score)
score_age = woeall["age"] * (-B*lr.coef_[0][0])
print(score_age)

可以通过循环，将所有特征的评分卡内容全部一次性写往一个本地文件ScoreData.csv：

file = "D:/datasets/ScoreData.csv"
#open是用来打开文件的python命令，第一个参数是文件的路径+文件名，如果文件是放在根目录下，则只需要文件名就好
#第二个参数是打开文件后的用途，"w"表示用于写入，通常使用的是"r"，表示打开来阅读
#首先写入基准分数
#之后使用循环，每次生成一组score_age类似的分档和分数，不断写入文件之中
with open(file,"w") as fdata:
    fdata.write("base_score,{}\n".format(base_score))
for i,col in enumerate(X.columns):
    score = woeall[col] * (-B*lr.coef_[0][i])
    score.name = "Score"
    score.index.name = col
    score.to_csv(file,header=True,mode="a")

至此，评分卡的内容就全部结束了。其实可以发现，真正建模的部分不多，更多是如何处理数据，如何利用统计和机器学习的方法将数据调整成希望的样子，所以除了算法，更加重要的是能够达成数据目的的工程能力。这份代码也还有很多细节可以改进，大家在使用的时候可以多找bug多修正，敢于挑战现有的内容，写出属于自己的分箱函数和评分卡模型。

四、附录：

4.1 逻辑回归的参数列表




4.2 逻辑回归的属性列表

4.3 逻辑回归的接口列表