机器学习基础之《分类算法（7）—案例：泰坦尼克号乘客生存预测》

一、泰坦尼克号数据

1、案例背景
泰坦尼克号沉没是历史上最臭名昭着的沉船之一。1912年4月15日，在她的处女航中，泰坦尼克号在与冰山相撞后沉没，在2224名乘客和机组人员中造成1502人死亡。这场耸人听闻的悲剧震惊了国际社会，并为船舶制定了更好的安全规定。 造成海难失事的原因之一是乘客和机组人员没有足够的救生艇。尽管幸存下沉有一些运气因素，但有些人比其他人更容易生存，例如妇女，儿童和上流社会。 在这个案例中，我们要求您完成对哪些人可能存活的分析。特别是，我们要求您运用机器学习工具来预测哪些乘客幸免于悲剧。

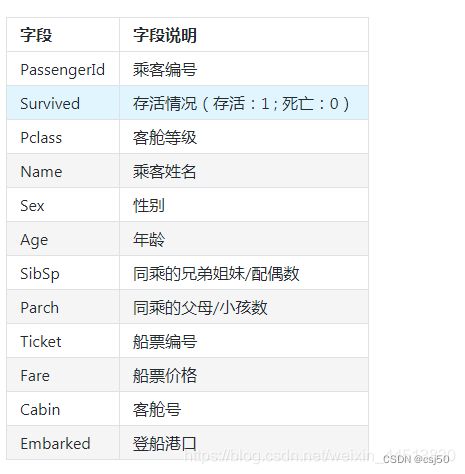
2、数据集字段
Pclass：乘客班（1，2，3）是社会经济阶层的代表
Age：数据有缺失

二、流程分析

1、获取数据
2、数据处理
  缺失值处理
  特征值 --> 字典类型
3、准备好特征值、目标值
4、划分数据集
5、特征工程：字典特征抽取
  决策树不需要做标准化
6、决策树预估器流程
7、模型评估

三、文件数据说明

1、gender_submission.csv  test.csv  train.csv，文件内容例子如下
train.csv：

PassengerId,Survived,Pclass,Name,Sex,Age,SibSp,Parch,Ticket,Fare,Cabin,Embarked
1,0,3,"Braund, Mr. Owen Harris",male,22,1,0,A/5 21171,7.25,,S
2,1,1,"Cumings, Mrs. John Bradley (Florence Briggs Thayer)",female,38,1,0,PC 17599,71.2833,C85,C
3,1,3,"Heikkinen, Miss. Laina",female,26,0,0,STON/O2. 3101282,7.925,,S
4,1,1,"Futrelle, Mrs. Jacques Heath (Lily May Peel)",female,35,1,0,113803,53.1,C123,S
5,0,3,"Allen, Mr. William Henry",male,35,0,0,373450,8.05,,S
6,0,3,"Moran, Mr. James",male,,0,0,330877,8.4583,,Q
7,0,1,"McCarthy, Mr. Timothy J",male,54,0,0,17463,51.8625,E46,S
8,0,3,"Palsson, Master. Gosta Leonard",male,2,3,1,349909,21.075,,S
9,1,3,"Johnson, Mrs. Oscar W (Elisabeth Vilhelmina Berg)",female,27,0,2,347742,11.1333,,S
......

test.csv：

PassengerId,Pclass,Name,Sex,Age,SibSp,Parch,Ticket,Fare,Cabin,Embarked
892,3,"Kelly, Mr. James",male,34.5,0,0,330911,7.8292,,Q
893,3,"Wilkes, Mrs. James (Ellen Needs)",female,47,1,0,363272,7,,S
894,2,"Myles, Mr. Thomas Francis",male,62,0,0,240276,9.6875,,Q
895,3,"Wirz, Mr. Albert",male,27,0,0,315154,8.6625,,S
896,3,"Hirvonen, Mrs. Alexander (Helga E Lindqvist)",female,22,1,1,3101298,12.2875,,S
897,3,"Svensson, Mr. Johan Cervin",male,14,0,0,7538,9.225,,S
898,3,"Connolly, Miss. Kate",female,30,0,0,330972,7.6292,,Q
899,2,"Caldwell, Mr. Albert Francis",male,26,1,1,248738,29,,S
900,3,"Abrahim, Mrs. Joseph (Sophie Halaut Easu)",female,18,0,0,2657,7.2292,,C
......

 gender_submission.csv：

PassengerId,Survived
892,0
893,1
894,0
895,0
896,1
897,0
898,1
899,0
900,1
......

2、字段说明

四、代码

import pandas as pd

# 1、获取数据
data_train = pd.read_csv("titanic_泰坦尼克数据集/train.csv")
data_test = pd.read_csv("titanic_泰坦尼克数据集/test.csv")

data_train.head()

# 筛选特征值和目标值
x = data_train[["Pclass", "Age", "Sex"]]
y = data_train["Survived"]

x.head()

y.head()

# 2、数据处理
# （1）缺失值处理
# 填补平均值，就地修改原对象
x["Age"].fillna(x["Age"].mean(), inplace=True)

x

# DataFrame转换为字典
x = x.to_dict(orient="records")

x

# （2）划分数据集
# 文件已经给了train.csv、test.csv
# 对test.csv做同样的处理，只获取特征值
m = data_test[["Pclass", "Age", "Sex"]]
m["Age"].fillna(m["Age"].mean(), inplace=True)

m = m.to_dict(orient="records")

m

# 3、字典特征抽取
from sklearn.feature_extraction import DictVectorizer
transfer = DictVectorizer()
x = transfer.fit_transform(x)
m = transfer.transform(m)

# 4、决策树预估器
from sklearn.tree import DecisionTreeClassifier, export_graphviz
estimator = DecisionTreeClassifier(criterion='entropy',max_depth=8)
estimator.fit(x, y)

# 5、获取测试集的目标值
data_test_n = pd.read_csv("titanic_泰坦尼克数据集/gender_submission.csv")
n = data_test_n["Survived"]

n.head()

# 6、模型评估
# 方法1：直接比对真实值和预测值
y_predict = estimator.predict(m)
print("y_predict：\n", y_predict)
print("直接比对真实值和预测值：\n", n == y_predict)
# 方法2：计算准确率
score = estimator.score(m, n)
print("准确率为：\n", score)

# 7、# 可视化决策树
export_graphviz(estimator, out_file='titanic_tree.dot', feature_names=transfer.get_feature_names())

运行结果：

运行后生成titanic_tree.dot文件：

digraph Tree {
node [shape=box] ;
0 [label="Sex=male <= 0.5\nentropy = 0.961\nsamples = 891\nvalue = [549, 342]"] ;
1 [label="Pclass <= 2.5\nentropy = 0.824\nsamples = 314\nvalue = [81, 233]"] ;
0 -> 1 [labeldistance=2.5, labelangle=45, headlabel="True"] ;
2 [label="Age <= 2.5\nentropy = 0.299\nsamples = 170\nvalue = [9, 161]"] ;
1 -> 2 ;
3 [label="Pclass <= 1.5\nentropy = 1.0\nsamples = 2\nvalue = [1, 1]"] ;
2 -> 3 ;
4 [label="entropy = 0.0\nsamples = 1\nvalue = [1, 0]"] ;
3 -> 4 ;
5 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
3 -> 5 ;
6 [label="Age <= 23.5\nentropy = 0.276\nsamples = 168\nvalue = [8, 160]"] ;
2 -> 6 ;
7 [label="entropy = 0.0\nsamples = 40\nvalue = [0, 40]"] ;
6 -> 7 ;
8 [label="Age <= 27.5\nentropy = 0.337\nsamples = 128\nvalue = [8, 120]"] ;
6 -> 8 ;
9 [label="Age <= 24.5\nentropy = 0.722\nsamples = 20\nvalue = [4, 16]"] ;
8 -> 9 ;
10 [label="Pclass <= 1.5\nentropy = 0.414\nsamples = 12\nvalue = [1, 11]"] ;
9 -> 10 ;
11 [label="entropy = 0.0\nsamples = 5\nvalue = [0, 5]"] ;
10 -> 11 ;
12 [label="entropy = 0.592\nsamples = 7\nvalue = [1, 6]"] ;
10 -> 12 ;
13 [label="Pclass <= 1.5\nentropy = 0.954\nsamples = 8\nvalue = [3, 5]"] ;
9 -> 13 ;
14 [label="Age <= 25.5\nentropy = 1.0\nsamples = 2\nvalue = [1, 1]"] ;
13 -> 14 ;
15 [label="entropy = 0.0\nsamples = 1\nvalue = [1, 0]"] ;
14 -> 15 ;
16 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
14 -> 16 ;
17 [label="Age <= 25.5\nentropy = 0.918\nsamples = 6\nvalue = [2, 4]"] ;
13 -> 17 ;
18 [label="entropy = 0.0\nsamples = 2\nvalue = [0, 2]"] ;
17 -> 18 ;
19 [label="entropy = 1.0\nsamples = 4\nvalue = [2, 2]"] ;
17 -> 19 ;
20 [label="Age <= 37.0\nentropy = 0.229\nsamples = 108\nvalue = [4, 104]"] ;
8 -> 20 ;
21 [label="entropy = 0.0\nsamples = 56\nvalue = [0, 56]"] ;
20 -> 21 ;
22 [label="Pclass <= 1.5\nentropy = 0.391\nsamples = 52\nvalue = [4, 48]"] ;
20 -> 22 ;
23 [label="Age <= 49.5\nentropy = 0.187\nsamples = 35\nvalue = [1, 34]"] ;
22 -> 23 ;
24 [label="entropy = 0.0\nsamples = 20\nvalue = [0, 20]"] ;
23 -> 24 ;
25 [label="entropy = 0.353\nsamples = 15\nvalue = [1, 14]"] ;
23 -> 25 ;
26 [label="Age <= 39.0\nentropy = 0.672\nsamples = 17\nvalue = [3, 14]"] ;
22 -> 26 ;
27 [label="entropy = 0.0\nsamples = 1\nvalue = [1, 0]"] ;
26 -> 27 ;
28 [label="entropy = 0.544\nsamples = 16\nvalue = [2, 14]"] ;
26 -> 28 ;
29 [label="Age <= 38.5\nentropy = 1.0\nsamples = 144\nvalue = [72, 72]"] ;
1 -> 29 ;
30 [label="Age <= 1.5\nentropy = 0.996\nsamples = 132\nvalue = [61, 71]"] ;
29 -> 30 ;
31 [label="entropy = 0.0\nsamples = 4\nvalue = [0, 4]"] ;
30 -> 31 ;
32 [label="Age <= 3.5\nentropy = 0.998\nsamples = 128\nvalue = [61, 67]"] ;
30 -> 32 ;
33 [label="Age <= 2.5\nentropy = 0.722\nsamples = 5\nvalue = [4, 1]"] ;
32 -> 33 ;
34 [label="entropy = 0.811\nsamples = 4\nvalue = [3, 1]"] ;
33 -> 34 ;
35 [label="entropy = 0.0\nsamples = 1\nvalue = [1, 0]"] ;
33 -> 35 ;
36 [label="Age <= 5.5\nentropy = 0.996\nsamples = 123\nvalue = [57, 66]"] ;
32 -> 36 ;
37 [label="entropy = 0.0\nsamples = 6\nvalue = [0, 6]"] ;
36 -> 37 ;
38 [label="Age <= 12.0\nentropy = 1.0\nsamples = 117\nvalue = [57, 60]"] ;
36 -> 38 ;
39 [label="entropy = 0.0\nsamples = 8\nvalue = [8, 0]"] ;
38 -> 39 ;
40 [label="Age <= 32.5\nentropy = 0.993\nsamples = 109\nvalue = [49, 60]"] ;
38 -> 40 ;
41 [label="entropy = 0.996\nsamples = 104\nvalue = [48, 56]"] ;
40 -> 41 ;
42 [label="entropy = 0.722\nsamples = 5\nvalue = [1, 4]"] ;
40 -> 42 ;
43 [label="Age <= 55.5\nentropy = 0.414\nsamples = 12\nvalue = [11, 1]"] ;
29 -> 43 ;
44 [label="entropy = 0.0\nsamples = 11\nvalue = [11, 0]"] ;
43 -> 44 ;
45 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
43 -> 45 ;
46 [label="Pclass <= 1.5\nentropy = 0.699\nsamples = 577\nvalue = [468, 109]"] ;
0 -> 46 [labeldistance=2.5, labelangle=-45, headlabel="False"] ;
47 [label="Age <= 17.5\nentropy = 0.95\nsamples = 122\nvalue = [77, 45]"] ;
46 -> 47 ;
48 [label="entropy = 0.0\nsamples = 4\nvalue = [0, 4]"] ;
47 -> 48 ;
49 [label="Age <= 53.0\nentropy = 0.932\nsamples = 118\nvalue = [77, 41]"] ;
47 -> 49 ;
50 [label="Age <= 22.5\nentropy = 0.968\nsamples = 96\nvalue = [58, 38]"] ;
49 -> 50 ;
51 [label="entropy = 0.0\nsamples = 5\nvalue = [5, 0]"] ;
50 -> 51 ;
52 [label="Age <= 27.5\nentropy = 0.98\nsamples = 91\nvalue = [53, 38]"] ;
50 -> 52 ;
53 [label="Age <= 24.5\nentropy = 0.881\nsamples = 10\nvalue = [3, 7]"] ;
52 -> 53 ;
54 [label="Age <= 23.5\nentropy = 0.918\nsamples = 3\nvalue = [2, 1]"] ;
53 -> 54 ;
55 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
54 -> 55 ;
56 [label="entropy = 0.0\nsamples = 2\nvalue = [2, 0]"] ;
54 -> 56 ;
57 [label="Age <= 26.5\nentropy = 0.592\nsamples = 7\nvalue = [1, 6]"] ;
53 -> 57 ;
58 [label="entropy = 0.0\nsamples = 3\nvalue = [0, 3]"] ;
57 -> 58 ;
59 [label="entropy = 0.811\nsamples = 4\nvalue = [1, 3]"] ;
57 -> 59 ;
60 [label="Age <= 47.5\nentropy = 0.96\nsamples = 81\nvalue = [50, 31]"] ;
52 -> 60 ;
61 [label="Age <= 45.25\nentropy = 0.923\nsamples = 68\nvalue = [45, 23]"] ;
60 -> 61 ;
62 [label="entropy = 0.956\nsamples = 61\nvalue = [38, 23]"] ;
61 -> 62 ;
63 [label="entropy = 0.0\nsamples = 7\nvalue = [7, 0]"] ;
61 -> 63 ;
64 [label="Age <= 48.5\nentropy = 0.961\nsamples = 13\nvalue = [5, 8]"] ;
60 -> 64 ;
65 [label="entropy = 0.0\nsamples = 3\nvalue = [0, 3]"] ;
64 -> 65 ;
66 [label="entropy = 1.0\nsamples = 10\nvalue = [5, 5]"] ;
64 -> 66 ;
67 [label="Age <= 75.5\nentropy = 0.575\nsamples = 22\nvalue = [19, 3]"] ;
49 -> 67 ;
68 [label="Age <= 60.5\nentropy = 0.454\nsamples = 21\nvalue = [19, 2]"] ;
67 -> 68 ;
69 [label="Age <= 55.5\nentropy = 0.722\nsamples = 10\nvalue = [8, 2]"] ;
68 -> 69 ;
70 [label="entropy = 0.0\nsamples = 3\nvalue = [3, 0]"] ;
69 -> 70 ;
71 [label="Age <= 59.0\nentropy = 0.863\nsamples = 7\nvalue = [5, 2]"] ;
69 -> 71 ;
72 [label="entropy = 0.722\nsamples = 5\nvalue = [4, 1]"] ;
71 -> 72 ;
73 [label="entropy = 1.0\nsamples = 2\nvalue = [1, 1]"] ;
71 -> 73 ;
74 [label="entropy = 0.0\nsamples = 11\nvalue = [11, 0]"] ;
68 -> 74 ;
75 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
67 -> 75 ;
76 [label="Age <= 9.5\nentropy = 0.586\nsamples = 455\nvalue = [391, 64]"] ;
46 -> 76 ;
77 [label="Pclass <= 2.5\nentropy = 0.987\nsamples = 30\nvalue = [13, 17]"] ;
76 -> 77 ;
78 [label="entropy = 0.0\nsamples = 9\nvalue = [0, 9]"] ;
77 -> 78 ;
79 [label="Age <= 0.71\nentropy = 0.959\nsamples = 21\nvalue = [13, 8]"] ;
77 -> 79 ;
80 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
79 -> 80 ;
81 [label="Age <= 2.5\nentropy = 0.934\nsamples = 20\nvalue = [13, 7]"] ;
79 -> 81 ;
82 [label="Age <= 1.5\nentropy = 0.65\nsamples = 6\nvalue = [5, 1]"] ;
81 -> 82 ;
83 [label="entropy = 0.918\nsamples = 3\nvalue = [2, 1]"] ;
82 -> 83 ;
84 [label="entropy = 0.0\nsamples = 3\nvalue = [3, 0]"] ;
82 -> 84 ;
85 [label="Age <= 3.5\nentropy = 0.985\nsamples = 14\nvalue = [8, 6]"] ;
81 -> 85 ;
86 [label="entropy = 0.0\nsamples = 2\nvalue = [0, 2]"] ;
85 -> 86 ;
87 [label="Age <= 8.5\nentropy = 0.918\nsamples = 12\nvalue = [8, 4]"] ;
85 -> 87 ;
88 [label="entropy = 0.811\nsamples = 8\nvalue = [6, 2]"] ;
87 -> 88 ;
89 [label="entropy = 1.0\nsamples = 4\nvalue = [2, 2]"] ;
87 -> 89 ;
90 [label="Age <= 32.25\nentropy = 0.502\nsamples = 425\nvalue = [378, 47]"] ;
76 -> 90 ;
91 [label="Age <= 30.75\nentropy = 0.552\nsamples = 320\nvalue = [279, 41]"] ;
90 -> 91 ;
92 [label="Pclass <= 2.5\nentropy = 0.501\nsamples = 299\nvalue = [266, 33]"] ;
91 -> 92 ;
93 [label="Age <= 29.35\nentropy = 0.318\nsamples = 52\nvalue = [49, 3]"] ;
92 -> 93 ;
94 [label="Age <= 20.0\nentropy = 0.176\nsamples = 38\nvalue = [37, 1]"] ;
93 -> 94 ;
95 [label="entropy = 0.469\nsamples = 10\nvalue = [9, 1]"] ;
94 -> 95 ;
96 [label="entropy = 0.0\nsamples = 28\nvalue = [28, 0]"] ;
94 -> 96 ;
97 [label="Age <= 29.85\nentropy = 0.592\nsamples = 14\nvalue = [12, 2]"] ;
93 -> 97 ;
98 [label="entropy = 0.764\nsamples = 9\nvalue = [7, 2]"] ;
97 -> 98 ;
99 [label="entropy = 0.0\nsamples = 5\nvalue = [5, 0]"] ;
97 -> 99 ;
100 [label="Age <= 29.35\nentropy = 0.534\nsamples = 247\nvalue = [217, 30]"] ;
92 -> 100 ;
101 [label="Age <= 24.75\nentropy = 0.581\nsamples = 144\nvalue = [124, 20]"] ;
100 -> 101 ;
102 [label="entropy = 0.479\nsamples = 97\nvalue = [87, 10]"] ;
101 -> 102 ;
103 [label="entropy = 0.747\nsamples = 47\nvalue = [37, 10]"] ;
101 -> 103 ;
104 [label="Age <= 30.25\nentropy = 0.46\nsamples = 103\nvalue = [93, 10]"] ;
100 -> 104 ;
105 [label="entropy = 0.463\nsamples = 102\nvalue = [92, 10]"] ;
104 -> 105 ;
106 [label="entropy = 0.0\nsamples = 1\nvalue = [1, 0]"] ;
104 -> 106 ;
107 [label="Age <= 31.5\nentropy = 0.959\nsamples = 21\nvalue = [13, 8]"] ;
91 -> 107 ;
108 [label="Pclass <= 2.5\nentropy = 0.863\nsamples = 7\nvalue = [5, 2]"] ;
107 -> 108 ;
109 [label="entropy = 0.811\nsamples = 4\nvalue = [3, 1]"] ;
108 -> 109 ;
110 [label="entropy = 0.918\nsamples = 3\nvalue = [2, 1]"] ;
108 -> 110 ;
111 [label="Pclass <= 2.5\nentropy = 0.985\nsamples = 14\nvalue = [8, 6]"] ;
107 -> 111 ;
112 [label="entropy = 0.918\nsamples = 3\nvalue = [2, 1]"] ;
111 -> 112 ;
113 [label="entropy = 0.994\nsamples = 11\nvalue = [6, 5]"] ;
111 -> 113 ;
114 [label="Age <= 38.5\nentropy = 0.316\nsamples = 105\nvalue = [99, 6]"] ;
90 -> 114 ;
115 [label="Pclass <= 2.5\nentropy = 0.162\nsamples = 42\nvalue = [41, 1]"] ;
114 -> 115 ;
116 [label="Age <= 34.5\nentropy = 0.337\nsamples = 16\nvalue = [15, 1]"] ;
115 -> 116 ;
117 [label="Age <= 33.5\nentropy = 0.544\nsamples = 8\nvalue = [7, 1]"] ;
116 -> 117 ;
118 [label="entropy = 0.0\nsamples = 2\nvalue = [2, 0]"] ;
117 -> 118 ;
119 [label="entropy = 0.65\nsamples = 6\nvalue = [5, 1]"] ;
117 -> 119 ;
120 [label="entropy = 0.0\nsamples = 8\nvalue = [8, 0]"] ;
116 -> 120 ;
121 [label="entropy = 0.0\nsamples = 26\nvalue = [26, 0]"] ;
115 -> 121 ;
122 [label="Age <= 45.25\nentropy = 0.4\nsamples = 63\nvalue = [58, 5]"] ;
114 -> 122 ;
123 [label="Age <= 44.5\nentropy = 0.544\nsamples = 32\nvalue = [28, 4]"] ;
122 -> 123 ;
124 [label="Age <= 43.5\nentropy = 0.469\nsamples = 30\nvalue = [27, 3]"] ;
123 -> 124 ;
125 [label="entropy = 0.402\nsamples = 25\nvalue = [23, 2]"] ;
124 -> 125 ;
126 [label="entropy = 0.722\nsamples = 5\nvalue = [4, 1]"] ;
124 -> 126 ;
127 [label="entropy = 1.0\nsamples = 2\nvalue = [1, 1]"] ;
123 -> 127 ;
128 [label="Age <= 61.5\nentropy = 0.206\nsamples = 31\nvalue = [30, 1]"] ;
122 -> 128 ;
129 [label="entropy = 0.0\nsamples = 25\nvalue = [25, 0]"] ;
128 -> 129 ;
130 [label="Age <= 63.5\nentropy = 0.65\nsamples = 6\nvalue = [5, 1]"] ;
128 -> 130 ;
131 [label="entropy = 0.0\nsamples = 1\nvalue = [0, 1]"] ;
130 -> 131 ;
132 [label="entropy = 0.0\nsamples = 5\nvalue = [5, 0]"] ;
130 -> 132 ;
}

转换成图像：

可以看到图像非常大。可以设置最大深度（例如：max_depth=8），用网格搜索来调试

五、决策树总结

1、优点：
简单的理解和解释，树木可视化。

2、缺点：
决策树学习者可以创建不能很好地推广数据的过于复杂的树，这被称为过拟合。

3、改进：
减枝cart算法(决策树API当中已经实现，随机森林参数调优有相关介绍)
随机森林

注：企业重要决策，由于决策树很好的分析能力，在决策过程应用较多，可以选择特征

六、其他：记录下fit_transform和transform的区别

1、二者区别
fit()，用来求得训练集X的均值，方差，最大值，最小值，这些训练集X固有的属性。
transform()，在fit的基础上，进行标准化，降维，归一化等操作。
fit_transform()，包含上述两个功能。

2、为什么训练集用fit_transform而测试集用transform
训练集已经通过fit_transform求出了一些固有属性，测试集可沿用上述属性直接标准化，不必重新再求。
x_train=std_x.fit_transform(x_train)
x_test=std_x.transform(x_test)