资料加载中

《统计学习方法》学习笔记之第一章

统计学习方法的学习笔记：第一章

第一节统计学习的定义与分类

统计学习的概念

统计学习的分类

第二节统计学习方法的基本分类

监督学习

无监督学习

强化学习

第三节统计学习方法三要素

模型

策略

第四节模型评估与模型选择

训练误差与测试误差

过拟合与模型选择

第五节正则化和交叉验证

正则化：实现结构风险最小化策略

交叉验证

第六节泛化能力

泛化误差

泛化误差上界

二分类问题

第七节生成模型与判别模型

生成模型和判别模型

生成模型VS判别模型

第八节监督学习的应用

分类问题

标注问题

回归问题

第一节统计学习的定义与分类

统计学习的概念

以计算机和网络为平台
以数据为研究对象
以预测和分析数据为目的
以方法为中心
是多领域交叉的学科

定义：

统计学习(Statistical Machine Learning)是关于计算机基于数据后见概率统计模型并运用模型对数据进行预测与分析的一门学科。

统计学习方法的具体步骤：

得到一个有限的训练数据集合
确定学习模型的集合(模型)
确定模型选择的准则(策略)
实现求解最优模型的算法(算法)
通过学习方法选择最优模型
利用学习的最有名模型对新数据进行预测和分析

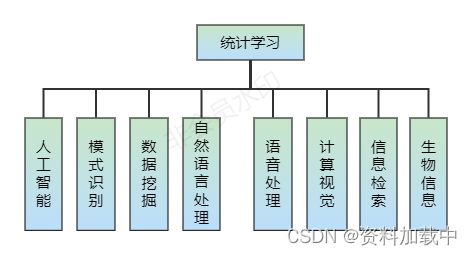
统计学习的分类

第二节统计学习方法的基本分类

监督学习

定义：监督学习(Supervised Learning)是指从标注数据中学习预测模型的机器学习问题，其本质是学习输入到输出的映射的统计规律。

输入空间(Input Space):输入的所有可能取值的集合
实例(Instance):每一个具体的输入，通常由特征向量(Feature Vector)表示
特征空间(Feature Space):所有特征向量存在的空间
输出空间(Output Space):输出的所有可能取值的集合

例：核技巧

输入空间：; 实例： $x=(x^{(1)},x^{2)})^T$

$\phi (x):R^2\rightarrow {H};$ $\phi{(x)}=((x^{(1)})^2,\sqrt{2}x^{(1)}x^{(2)},(x^{(2)})^2)^T$

根据变量类型不同：

-输入变量与输出变量均为连续变量的预测问题(回归问题)

-输出变量为有限个离散变量的预测问题(分类问题)

-输入变量与输出变量均为变量序列的预测问题(标注问题)

符号表示

输入变量：X;输入变量的取值：x
输出变量：Y;输出变量的取值：y
输入实例x的特征向量表示：

$x=(x^{(1)},x^{(2)},...,x^{(j)},...,x^{(n)})^T$

以表示多个输入变量中的第i个变量：

$x_i=(x_i^{(1)},x_i^{(2)},...,x_i^{(j)},...,x_i^{(n)})^T$

样本容量为N的训练集：

$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$

监督学习的基本假设：X和Y具有联合概率分布P(X,Y)
监督学习的目的：学习一个输入到输出的映射，这一映射以模型表示
模型的形式：条件概率分布P(Y|X)或决策函数Y=f(X)
假设空间(Hypothesis Space):所有这些可能模型的集合

对具体的输入进行相应的输出与测试，表达为：

P(y|x)或y=f(x)

无监督学习

定义：无监督学习(Unsupervised Learning)是指从无标注数据中学习预测模型的机器学习问题，其本质是学习数据中的统计规律或潜在结构。

监督学习VS无监督学习

输入空间： $\chi$
隐式结构空间：
模型：函数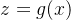,条件概率分明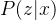或条件概率分布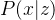
假设空间(Hypothesis Space)：所有这些可能模型的集合
目的：选出在给定评价标准下的最优模型
样本容量为N的训练集：

$U={x_1,x_2,...,x_N}$

强化学习

第三节统计学习方法三要素

统计学习方法=模型+策略+算法

模型

定义：假设空间(Hypothesis Space):所有可能的条件概率分布或决策函数，用F表示

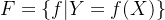
若定义为决策函数的集合： $F=\{f|Y=f(X)\}$
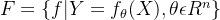
F是有一个参数向量决定的函数族构成： $F=\{f|Y=f_\theta(X),\theta\epsilon R^n\}$
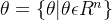
参数空间： $\theta = \{\theta|\theta\epsilon R^n\}$

例：线性回归

实例： $x=(x^{(1)},x^{(2)},...,x^{(n)})^T$

决策函数： $f(x)=w^{(1)}x^{(1)}+w^{(2)}x^{(2)}+...+w^{(n)}x^{(n)}+b$

向量形式： $f(x)=w\cdot x+b$ ,其中， $w=(W^{(1)},w^{(2)},...,w^{(n)})$

若定义为条件概率的集合：

F由一个参数向量决定的条件概率分布族构成：

$F=\{P|P_\theta(Y|X),\theta\epsilon R^n\}$

例：Logistic回归

实例： $x=(x^{(1)},x^{(2)},...,x^{(n)})^T$

条件概率分布：

策略

损失函数：度量模型一次预测的好坏，记作

风险函数：度量平均意义下模型预测的好坏

$R_{exp}(f) = E_p{[L(Y, f(x))]} \\$

经验风险：模型关于训练集的平均损失

$\frac{1}{N}\sum\limits_{i=1}^NL(y_i, f(x_i))$

其中，训练集 $T = \{(x_1, y_1), (x_2, y_2),...,(x_N, y_N)\}$

四种常见的损失函数

0-1损失函数（分类问题）
平方损失函数（回归问题）
绝对损失函数（回归问题）
对数损失函数（概率模型）

经验风险最小化：

$\min\limits_{ f\epsilon F}\frac{1}{N}L(y_i, f(x_i))$

结构风险：

$R_{srm} = \frac{1}{N}L(y_i, f(x_i)) + \lambda J(f)$

结构风险最小化：

$\min\limits_{f\epsilon F}\frac{1}{N}L(y_i, f(x_i)) + \lambda J(f))$

根据大数定律，当样本容量N->正无穷时，经验风险趋近于风险函数

结构风险在经验风险的基础上加了正则项（针对模型的复杂度），平衡了经验风险和模型的复杂度

选取目标函数：经验风险函数或者结构风险函数

最优模型：不存在显示解析解的情况下，可以使用梯度下降的数值运算方法

第四节模型评估与模型选择

训练误差与测试误差

1. 训练误差

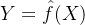
学习到的模型: $Y=\hat f(X)$
训练集（Training Set）:

$T = \{(x_1, y_1),(x_2, y_2),(x_N, y_N)\}$

训练误差（Training Error）：

$R_{emp}(\hat f) = \frac{1}{N}\sum\limits_{i=1}^NL(y_i, \hat f(x_i))$

2. 测试误差

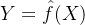
学习到的模型: $Y=\hat f(X)$
训练集（Test Set）:

${T}' =\{({x_1}', {y_1}'),({x_2}', {y_2}'),...,({x_N}', {y_N}')\}$

训练误差（Test Error）：

$e_test = \frac{1}{{N}'} \sum\limits_{i'=1}^{N'}L(y_i',\hat f(x_{i'}))$

误差率(Error Rate):

$e_test = \frac{1}{N'}\sum\limits_{i'=1}^{N'}I(y_i \neq \hat f(x_{i'}))$

准确率(Accuracy):

$r_test = \frac{1}{N'}\sum\limits_{i'=1}^{N'}I(y_i=\hat f(x_{i'}))$

注：

$r_{test} + e_{test} = 1$

M次多项式：

$f_M(x, w)=w_0+w_1x+w_2x^2+...+w_Mx^M = \sum\limits_{j=0}^M w_jx^j$

经验风险：

$L(w) = \frac{1}{2}\sum\limits_{i=1}^N(f_M(x_i, w)-y_i)^2$

带入多项式：

$L(w) = \frac{1}{2}\sum\limits_{i=1}^N(\sum\limits_{j=0}^Mw_jx_i^j-y_i)^2$

通过最小二乘法求解参数。

过拟合与模型选择

过拟合（Over-Fitting）：学习所的模型包含参数过多，出现对已知数据预测很好，但对位置数据预测预测很差的现象。

第五节正则化和交叉验证

正则化：实现结构风险最小化策略

一般形式：

$\min\limits_{f\epsilon F}\frac{1}{N}\sum\limits_{i=1}^NL(y_i,f(x_i)) + \lambda J(f)$

经验风险：

$\frac{1}{N}\sum\limits_{i=1}^NL(y_i,f(x_i))$

正则化项：

$\lambda J(f)$

其中， $\lambda$ 权衡经验风险和模型复杂度

最常见的两种正则化项

范数：

$L(w)=\frac{1}{N}\sum\limits_{i=1}^N(f(x_i;w)-y_i)^2+\lambda ||w||_1$

其中， $||w||_1=\sum\limits_j|w_j|$

使某些参数为零，可以起到特征筛选的作用，稀疏模型，非零参数个数很少

范数：

$L(w)=\frac{1}{N}(f(x_i;w)-y_i)^2 + \frac{\lambda}{2}||w||_2^2$

其中， $||w||_2=\sqrt{\sum\limits_jw_j^2}, ||w||_2^2 = \sum\limits_jw_j^2$

参数可以无限接近于零，使得模型越来越简单，防止过拟合。

奥卡姆剃刀原理

在模型选择时，选择所有可能模型中，能很好解释已知数据并且十分简单的模型。

交叉验证

数据充足的情况下：

训练集(Training Set):用以训练模型
验证集(Validation Set):用以选择模型
测试集(Test Set):用以最终对学习方法的评估

数据不充足的情况下：

简单交叉验证：随机将数据分为两部分，即训练集和测试集
S折交叉验证：随机将数据分为S个互不相交、大小相同的子集，其中以S-1个子集作为训练集，余下的子集作为测试集
留一交叉验证：S折交叉验证的特殊情形，S=N，在数据非常缺乏的情况下使用

第六节泛化能力

泛化误差

若所学习到的模型是 $\hat f$ ,那么这个模型对未知数据预测的误差即为泛化误差(Generalization Error):

$R_{exp}(\hat f)=E_p{[Y, \hat f(X)]}=\int _{x\times y}L(y, \hat f(x))P(x, y)dxdy$

损失函数的期望值，所求的积分是在全样本上进行的

泛化误差上界

泛化误差上界(Generalization Error Bound)：指泛化误差的概率上界。两种学习方法的优劣，通常通过他们的泛化误差上界进行比较。

性质：

样本容量的函数：当样本容量增加时，泛化上界趋于0
假设空间容量的函数：假设空间容量越大，模型就越难学，泛化误差上界就越大

假设空间：所有可能的模型

例子：

二分类问题

训练数据集：

$T=\{(x_1,y_1),(x_2,y_2),...,(x_N,y_N)\}$

其中，T是从联合概率分布P(X,Y)独立同分布产生的， $X\epsilon R^n,Y \epsilon \{-1, +1\}$

假设空间：

$F = \{f_1, f_2,...,f_d\}$

其中，d是函数个数

假设 $f\epsilon F$ ,损失函数为0-1损失，

期望风险：

经验风险：

$\hat R(f) = \frac{1}{N}\sum\limits_{i=1}^NL(y_i,f(x_i))$

经验风险最小化：

$f_N =\arg \min\limits_{f\epsilon F}\hat R(f)$

的泛化能力：

$R(f_N)=E{[L(Y,f_N(X))]}$

定理(泛化误差上界)：

对于二分类问题，当假设空间是有限个函数的集合 $F = \{f_1, f_2,...,f_d\}$ 时，对于 $\forall f\epsilon F$ ,至少以概率 $1-\delta$ , $0 < \delta < 1$ ,以下不等式成立：

$R(f)\leq \hat R(f)+\varepsilon (d,N,\delta)$

训练误差 $\hat R(f)$ ，泛化误差上界 $\varepsilon (d,N,\delta)$

其中，

$\varepsilon(d,N,\delta)=\sqrt{\frac{1}{2N}(logd+log\frac{1}{\delta})}$

d为假设空间中函数的个数，N表示i训练集中的样本个数；N趋于无穷大，趋于0；当d趋于无穷大时，即假设空间越来越复杂时，泛化误差上界增大。

泛化误差上界定理证明：

Hoeffding不等式(第一版)

设是独立随机变量，且 $X_i\epsilon[a_i,b_i],i=1,2,...,N;S_n=\sum\limits_{i=1}^NX_i$ ,则对任意,以下不等式成立：

$P[S_N-E(S_N)\geq t] \leq \exp[-\frac{2t^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

$P[E(S_N)-S_N\geq t] \leq \exp[-\frac{2t^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

Hoeffding不等式(第二版)

设是独立随机变量，且 $X_i\epsilon[a_i,b_i],i=1,2,...,N;$ $\overline{X}$ 是的经验平均值， $\overline{X}=\frac{1}{N}\sum\limits_{i=1}^NX_i$ ,则对任意,以下不等式成立：

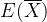$P[\overline{X}-E(\overline{X})\geq t] \leq \exp[-\frac{2N^2t^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

$P[E(\overline{X})-\overline{X}\geq t] \leq \exp[-\frac{2N^2t^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

第一版：

$P[S_N-E(S_N)\geq t] \leq \exp[-\frac{2t^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

$\Rightarrow P[\frac{S_N}{N}-E(\frac{S_N}{N})\geq \frac{t}{N}] \leq \exp[-\frac{2t^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

令 $\overline{X} = \frac{1}{N}\sum\limits_{i=1}^NX_i$ , $t' = \frac{t}{N}$ ,则 $\overline{X}=\frac{S_N}{N}$ ,,从而有，

$P[\overline{X}-E(\overline{X})\geq t'] \leq \exp[-\frac{2(t'N)^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

第二版：

$P[\overline{X}-E(\overline{X})\geq t] \leq \exp[-\frac{2N^2t^2}{\sum\limits_{i=1}^N(b_i-a_i)^2}]$

证明：

,则

$\overline{X}$ :

$\overline{X}=\frac{1}{N}\sum\limits_{i=1}^NL(y_i,f(x_i))$

$=\hat R(f)$

对所有的i,

$E(\overline{X})$ :

$E(\overline{X})=E(\frac{1}{N}\sum\limits_{i=1}^NL(y_i, f(x_i)))$

$=\frac{1}{N}\sum\limits_{i=1}^NE(L(y_i,f(x_i)))$

$=\frac{1}{N}\sum\limits_{i=1}^NE(L(Y,f(X)))$

根据Hoeffding不等式，对 $\varepsilon > 0$ ,有：

$P(R(f)-\hat R(f) \geq{\varepsilon}) \leq{\exp(-2N\varepsilon^2)}$

假设空间有限，则，

$P(\exists f\epsilon F:R(f)-\hat R(f) \geq \varepsilon)$

$=P(\bigcup\limits_{f\epsilon F}\{R(f)-\hat R(f)\geq{\varepsilon}\})$

$\leq{\sum\limits_{f\epsilon F}P(R(f)-\hat R(f))\geq\varepsilon}$

$\leq \exp(-2N\varepsilon^2)$

或者等价于， $\forall f \epsilon F,$

$P(R(f)-\hat R(f)<\varepsilon)\geq{1-d\exp(-2N\varepsilon^2)}$

令 $\delta=d \exp(-2N\varepsilon^2)$ ,

$P(R(f)) < \hat R(f)+\varepsilon) \geq 1-\delta$

又，

$\delta=d \exp(-2N\varepsilon^2)\Rightarrow \varepsilon^2=-\frac{1}{2N}\log(\frac{\delta}{d})=\frac{1}{2N}(\log d + \log \frac{1}{\delta})$

因此，对 $\forall f \epsilon F$ ,至少以概率 $1-\delta$ ，以下不等式成立：

$R(f)<\hat R(f)+\varepsilon (d, N, \delta)$

第七节生成模型与判别模型

生成模型和判别模型

生成模型

由数据学习联合概率分布P(X,Y)，然后求出P(Y|X)作为预测模型，即生成模型(Generative Model):

$P(Y|X) = \frac{P(X,Y)}{P(X)}$

典型的生成模型：朴素贝叶斯法、隐马尔可夫模型

注：输入和输出变量要求为随机变量

判别模型

由数据直接学习决策函数f(X)或者条件概率分布P(Y|X)作为预测模型，即判别模型(Discriminative Model)

典型的判别模型：k近邻法、感知机、决策树等

注：不需要输入和输出变量均为随机变量

生成模型VS判别模型

生成模型：

所需数据量较大
可还原联合概率分布P(X,Y)
收敛速度更快
能反映同类数据本身得相似度
隐变量存在时，仍可以使用生成模型

判别模型：

所需样本的数量少于生成模型
可直接面对预测，准确率更高
可见化学习问题
不可以反映数据本身的特性

第八节监督学习的应用

分类问题

分类准确率

对于给定的测试数据集，分类器正确分类的样本数与总样本数之比成为分类准确率：

$r_test = \frac{1}{N'}\sum\limits_{i'=1}^{N'}I(y_{i'}=\hat f(x_{i'}))$

I表示当预测出来的分类与真实的类别一致时为1，否则为0

二分类问题:

真实

预测

正类

负类

正类

负类

精确率：

$P=\frac{TP}{TP+FP}$

召回率：

$R=\frac{TP}{TP+FN}$

F1-Score:

$\frac{2}{F_1} = \frac{1}{P}+\frac{1}{R}$

分类方法：感知机、k近邻、朴素贝叶斯、决策树、Logistic回归

应用：银行业务、网络安全、图像处理、手写识别、互联网搜索

标注问题

训练集：

$T=\{(x_1,y_1),(x_2,y_2),...,(x_N, y_N)\}$

-输入观测序列：

$x_i=(x_i^{(1)},x_i^{(2)},x_i^{(3)},...,x_i^{(n)})^T,i=1,2,...,N$

-输出观测序列：

$y_i=(y_i^{(1)},y_i^{(2)},y_i^{(3)},...,y_i^{(n)})^T,i=1,2,...,N$

学习的模型：

$P(Y^{(1)},Y^{(2)},...,Y^{(n)}|X^{(1)},X^{(2)},...,X^{(n)})$

预测

-新的输入观测序列：

$x_{N+1} = (x_{N+1}^{(1)},x_{N+1}^{(2)},...,x_{N+1}^{(n)})^T$

-预测的输出标记序列：

$y_{N+1} = (y_{N+1}^{(1)},y_{N+1}^{(2)},...,y_{N+1}^{(n)})^T$

方法：

隐马尔可夫模型

条件随机场

应用：

信息抽取

自然语言处理

例：

输入：At Microsoft Research,we have an insatiable curiosity and the desire to create new technology that will help define the computing experience.

输出：At/O Microsoft/B Research/E,we/O have/O an/O insatiable/B curiosity/E and/O the/O desire/BE to/O create/O new/B technology/E that/O will/O help/O define/O the/O computing/B experience/E.

回归问题

反映输入和输出的映射问题。

类型：

-按输入变量个数：一元回归、多元回归

-按输入和输出变量之间关系：线性回归、非线性回归

损失函数：平方损失

应用领域：商务领域

参考资料：

《统计学习方法》第二版

参考视频：

【合集】十分钟机器学习系列视频《统计学习方法》_哔哩哔哩_bilibili

你可能感兴趣的:(机器学习,机器学习,算法,线性回归)

机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习 python
一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
Goolge earth studio 进阶4——路径修改与平滑陟彼高冈yu Google earth studio 进阶教程旅游
如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
基于社交网络算法优化的二维最大熵图像分割智能算法研学社（Jack旭）智能优化算法应用图像分割算法 php 开发语言
智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
121. 买卖股票的最佳时机薄荷糖的味道_fb40
给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
每日算法&面试题，大厂特训二十八天——第二十天（树）肥学 ⚡算法题⚡面试题每日精进 java 算法数据结构
目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
回溯算法-重新安排行程 chirou_ 算法数据结构图论 c++图搜索
leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
Faiss：高效相似性搜索与聚类的利器网络·魚大数据 faiss
Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
【华为OD技术面试真题 - 技术面】- python八股文真题题库（1）算法大师华为od 面试 python
华为OD面试真题精选专栏：华为OD面试真题精选目录:2024华为OD面试手撕代码真题目录以及八股文真题目录文章目录华为OD面试真题精选1.数据预处理流程数据预处理的主要步骤工具和库2.介绍线性回归、逻辑回归模型线性回归（LinearRegression）模型形式：关键点：逻辑回归（LogisticRegression）模型形式：关键点：参数估计与评估：3.python浅拷贝及深拷贝浅拷贝（Shal
数字里的世界17期：2021年全球10大顶级数据中心，中国移动榜首张三叨
你知道吗？2016年，全球的数据中心共计用电4160亿千瓦时，比整个英国的发电量还多40％！前言每天，我们都会创造超过250万TB的数据。并且随着物联网（IOT）的不断普及，这一数据将持续增长。如此庞大的数据被存储在被称为“数据中心”的专用设施中。虽然最早的数据中心建于20世纪40年代，但直到1997-2000年的互联网泡沫期间才逐渐成为主流。当前人类的技术，比如人工智能和机器学习，已经将我们推向
nosql数据库技术与应用知识点皆过客，揽星河 NoSQL nosql 数据库大数据数据分析数据结构非关系型数据库
Nosql知识回顾大数据处理流程数据采集(flume、爬虫、传感器)数据存储(本门课程NoSQL所处的阶段)Hdfs、MongoDB、HBase等数据清洗(入仓)Hive等数据处理、分析(Spark、Flink等)数据可视化数据挖掘、机器学习应用(Python、SparkMLlib等)大数据时代存储的挑战(三高)高并发(同一时间很多人访问)高扩展(要求随时根据需求扩展存储)高效率(要求读写速度快)
insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insert into select 主键自增 mybatis delete返回值 mybatis insert返回主键 mybatis insert返回对象 mybatis plus insert返回主键 mybatis plus 插入生成id
前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
Python开发常用的三方模块如下：换个网名有点难 python 开发语言
Python是一门功能强大的编程语言，拥有丰富的第三方库，这些库为开发者提供了极大的便利。以下是100个常用的Python库，涵盖了多个领域：1、NumPy，用于科学计算的基础库。2、Pandas，提供数据结构和数据分析工具。3、Matplotlib，一个绘图库。4、Scikit-learn，机器学习库。5、SciPy，用于数学、科学和工程的库。6、TensorFlow，由Google开发的开源机
Python实现简单的机器学习算法 master_chenchengg python python 办公效率 python开发 IT
Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习 K近邻
importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列 C语言
文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
[Python] 数据结构详解及代码 AIAdvocate 算法 python 数据结构链表
今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
Python算法L5：贪心算法小熊同学哦 Python算法算法 python 贪心算法
Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
遥感影像的切片处理 sand&wich 计算机视觉 python 图像处理
在遥感影像分析中，经常需要将大尺寸的影像切分成小片段，以便于进行详细的分析和处理。这种方法特别适用于机器学习和图像处理任务，如对象检测、图像分类等。以下是如何使用Python和OpenCV库来实现这一过程，同时确保每个影像片段保留正确的地理信息。准备环境首先，确保安装了必要的Python库，包括numpy、opencv-python和xml.etree.ElementTree。这些库将用于图像处理
【RabbitMQ 项目】服务端：数据管理模块之绑定管理月夜星辉雪 rabbitmq 分布式
文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
非对称加密算法原理与应用2——RSA私钥加密文件私语茶馆云部署与开发架构及产品灵感记录 RSA2048 私钥加密
作者：私语茶馆1.相关章节（1）非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对，并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容，包括从密钥库或文件中读取私钥，并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件，只能由该私钥对应的公钥来解密。
粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能 matlab 算法
在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
非对称加密算法————RSA理论及详情 hu19930613
转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
ai绘画工具midjourney怎么下载？附作品管理教程设计师早上好
Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
【加密算法基础——对称加密和非对称加密】 XWWW668899 网络安全服务器笔记
对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法，各自有不同的特点和用途。以下是详细比较：1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快，适合处理大量数据。实现:算法相对简单，计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
【算法练习】IDEA集成leetcode插件实现快速刷 2401_84102892 2024年程序员学习算法 intellij-idea leetcode
============点击右侧边leetcode->设置->配置地址、用户名、密码、存放目录、文件模板用户名要登录后在账号信息里看模板代码1.codefilename!velocityTool.camelC
[实践应用] 深度学习之模型性能评估指标 YuanDaima2048 深度学习工具使用深度学习人工智能损失函数性能评估 pytorch python 机器学习
文章总览：YuanDaiMa2048博客文章总览深度学习之模型性能评估指标分类任务回归任务排序任务聚类任务生成任务其他介绍在机器学习和深度学习领域，评估模型性能是一项至关重要的任务。不同的学习任务需要不同的性能指标来衡量模型的有效性。以下是对一些常见任务及其相应的性能评估指标的详细解释和总结。分类任务分类任务是指模型需要将输入数据分配到预定义的类别或标签中。以下是分类任务中常用的性能指标：准确率(
【加密算法基础——RSA 加密】 XWWW668899 网络服务器笔记 python
RSA加密RSA（Rivest-Shamir-Adleman）加密是非对称加密，一种广泛使用的公钥加密算法，主要用于安全数据传输。公钥用于加密，私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏：R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法，并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础，使得安全通
机器学习-聚类算法不良人龍木木机器学习机器学习算法聚类
机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记，感谢点赞关注！1.AHC2.K-means3.SC传统谱聚类：个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持！
linux系统服务器下jsp传参数乱码 3213213333332132 java jsp linux windows xml
在一次解决乱码问题中，发现jsp在windows下用js原生的方法进行编码没有问题，但是到了linux下就有问题， escape,encodeURI,encodeURIComponent等都解决不了问题但是我想了下既然原生的方法不行，我用el标签的方式对中文参数进行加密解密总该可以吧。于是用了java的java.net.URLDecoder,结果还是乱码，最后在绝望之际，用了下面的方法解决了
Spring 注解区别以及应用 BlueSkator spring
1. @Autowired @Autowired是根据类型进行自动装配的。如果当Spring上下文中存在不止一个UserDao类型的bean，或者不存在UserDao类型的bean，会抛出 BeanCreationException异常，这时可以通过在该属性上再加一个@Qualifier注解来声明唯一的id解决问题。 2. @Qualifier 当spring中存在至少一个匹
printf和sprintf的应用 dcj3sjt126com PHP sprintf printf
<?php printf('b: %b c: %c d: %d <bf>f: %f', 80,80, 80, 80); echo ' '; printf('%0.2f %+d %0.2f ', 8, 8, 1235.456); printf('th
config.getInitParameter 171815164 parameter
web.xml <servlet> <servlet-name>servlet1</servlet-name> <jsp-file>/index.jsp</jsp-file> <init-param> <param-name>str</param-name>
Ant标签详解--基础操作 g21121 ant
Ant的一些核心概念： build.xml：构建文件是以XML 文件来描述的，默认构建文件名为build.xml。 project：每个构建文
[简单]代码片段_数据合并 53873039oycg 代码
合并规则:删除家长phone为空的记录,若一个家长对应多个孩子,保留一条家长记录,家长id修改为phone,对应关系也要修改。代码如下:
java 通信技术云端月影 Java 远程通信技术
在分布式服务框架中，一个最基础的问题就是远程服务是怎么通讯的，在Java领域中有很多可实现远程通讯的技术，例如：RMI、MINA、ESB、Burlap、Hessian、SOAP、EJB和JMS等，这些名词之间到底是些什么关系呢，它们背后到底是基于什么原理实现的呢，了解这些是实现分布式服务框架的基础知识，而如果在性能上有高的要求的话，那深入了解这些技术背后的机制就是必须的了，在这篇blog中我们将来
string与StringBuilder 性能差距到底有多大 aijuans
之前也看过一些对string与StringBuilder的性能分析，总感觉这个应该对整体性能不会产生多大的影响，所以就一直没有关注这块！由于学程序初期最先接触的string拼接，所以就一直没改变过自己的习惯！
今天碰到 java.util.ConcurrentModificationException 异常 antonyup_2006 java 多线程工作 IBM
今天改bug，其中有个实现是要对map进行循环，然后有删除操作，代码如下： Iterator<ListItem> iter = ItemMap.keySet.iterator(); while(iter.hasNext()){ ListItem it = iter.next(); //...一些逻辑操作 ItemMap.remove(it); } 结果运行报Con
PL/SQL的类型和JDBC操作数据库百合不是茶 PL/SQL表标量类型游标 PL/SQL记录
PL/SQL的标量类型: 字符,数字,时间,布尔,%type五中类型的 --标量：数据库中预定义类型的变量 --定义一个变长字符串 v_ename varchar2(10); --定义一个小数,范围 -9999.99~9999.99 v_sal number(6,2); --定义一个小数并给一个初始值为5.4 :=是pl/sql的赋值号
Mockito：一个强大的用于 Java 开发的模拟测试框架实例 bijian1013 mockito 单元测试
Mockito框架： Mockito是一个基于MIT协议的开源java测试框架。 Mockito区别于其他模拟框架的地方主要是允许开发者在没有建立“预期”时验证被测系统的行为。对于mock对象的一个评价是测试系统的测
精通Oracle10编程SQL(10)处理例外 bijian1013 oracle 数据库 plsql
/* *处理例外 */ --例外简介 --处理例外-传递例外 declare v_ename emp.ename%TYPE; begin SELECT ename INTO v_ename FROM emp where empno=&no; dbms_output.put_line('雇员名：'||v_ename); exceptio
【Java】Java执行远程机器上Linux命令 bit1129 linux命令
Java使用ethz通过ssh2执行远程机器Linux上命令，封装定义Linux机器的环境信息 package com.tom; import java.io.File; public class Env { private String hostaddr; //Linux机器的IP地址 private Integer po
java通信之Socket通信基础白糖_ java socket 网络协议
正处于网络环境下的两个程序，它们之间通过一个交互的连接来实现数据通信。每一个连接的通信端叫做一个Socket。一个完整的Socket通信程序应该包含以下几个步骤： ①创建Socket； ②打开连接到Socket的输入输出流； ④按照一定的协议对Socket进行读写操作； ④关闭Socket。 Socket通信分两部分：服务器端和客户端。服务器端必须优先启动，然后等待soc
angular.bind boyitech AngularJS angular.bind AngularJS API bind
angular.bind 描述：上下文，函数以及参数动态绑定，返回值为绑定之后的函数. 其中args是可选的动态参数，self在fn中使用this调用。使用方法： angular.bind(se
java-13个坏人和13个好人站成一圈，数到7就从圈里面踢出一个来，要求把所有坏人都给踢出来，所有好人都留在圈里。请找出初始时坏人站的位置。 bylijinnan java
import java.util.ArrayList; import java.util.List; public class KickOutBadGuys { /** * 题目：13个坏人和13个好人站成一圈，数到7就从圈里面踢出一个来，要求把所有坏人都给踢出来，所有好人都留在圈里。请找出初始时坏人站的位置。 * Maybe you can find out
Redis.conf配置文件及相关项说明（自查备用） Kai_Ge redis
Redis.conf配置文件及相关项说明 # Redis configuration file example # Note on units: when memory size is needed, it is possible to specifiy # it in the usual form of 1k 5GB 4M and so forth: #
[强人工智能]实现大规模拓扑分析是实现强人工智能的前奏 comsci 人工智能
真不好意思,各位朋友...博客再次更新... 节点数量太少,网络的分析和处理能力肯定不足,在面对机器人控制的需求方面,显得力不从心.... 但是,节点数太多,对拓扑数据处理的要求又很高,设计目标也很高,实现起来难度颇大...
记录一些常用的函数 dai_lm java
public static String convertInputStreamToString(InputStream is) { StringBuilder result = new StringBuilder(); if (is != null) try { InputStreamReader inputReader = new InputStreamRead
Hadoop中小规模集群的并行计算缺陷 datamachine mapreduce hadoop 并行计算
注：写这篇文章的初衷是因为Hadoop炒得有点太热，很多用户现有数据规模并不适用于Hadoop，但迫于扩容压力和去IOE（Hadoop的廉价扩展的确非常有吸引力）而尝试。尝试永远是件正确的事儿，但有时候不用太突进，可以调优或调需求，发挥现有系统的最大效用为上策。 -----------------------------------------------------------------
小学4年级英语单词背诵第二课 dcj3sjt126com english word
egg 蛋 twenty 二十 any 任何 well 健康的，好 twelve 十二 farm 农场 every 每一个 back 向后，回 fast 快速的 whose 谁的 much 许多 flower 花 watch 手表 very 非常，很 sport 运动 Chinese 中国的
自己实践了github的webhooks, linux上面的权限需要注意 dcj3sjt126com github webhook
环境, 阿里云服务器 1. 本地创建项目, push到github服务器上面 2. 生成www用户的密钥 sudo -u www ssh-keygen -t rsa -C "[email protected]" 3. 将密钥添加到github帐号的SSH_KEYS里面 3. 用www用户执行克隆, 源使
Java冒泡排序蕃薯耀冒泡排序 Java冒泡排序 Java排序
冒泡排序 >>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>>> 蕃薯耀 2015年6月23日 10:40:14 星期二 http://fanshuyao.iteye.com/
Excle读取数据转换为实体List【基于apache-poi】 hanqunfeng apache
1.依赖apache-poi 2.支持xls和xlsx 3.支持按属性名称绑定数据值 4.支持从指定行、列开始读取 5.支持同时读取多个sheet 6.具体使用方式参见org.cpframework.utils.excelreader.CP_ExcelReaderUtilTest.java 比如： Str
3个处于草稿阶段的Javascript API介绍 jackyrong JavaScript
原文： http://www.sitepoint.com/3-new-javascript-apis-may-want-follow/?utm_source=html5weekly&utm_medium=email 本文中，介绍3个仍然处于草稿阶段，但应该值得关注的Javascript API. 1) Web Alarm API &
6个创建Web应用程序的高效PHP框架 lampcy Web 框架 PHP
以下是创建Web应用程序的PHP框架，有coder bay网站整理推荐： 1. CakePHP CakePHP是一个PHP快速开发框架，它提供了一个用于开发、维护和部署应用程序的可扩展体系。CakePHP使用了众所周知的设计模式，如MVC和ORM，降低了开发成本，并减少了开发人员写代码的工作量。 2. CodeIgniter CodeIgniter是一个非常小且功能强大的PHP框架，适合需
评"救市后中国股市新乱象泛起"谣言 nannan408
首先来看百度百家一位易姓作者的新闻：三个多星期来股市持续暴跌，跌得投资者及上市公司都处于极度的恐慌和焦虑中，都要寻找自保及规避风险的方式。面对股市之危机，政府突然进入市场救市，希望以此来重建市场信心，以此来扭转股市持续暴跌的预期。而政府进入市场后，由于市场运作方式发生了巨大变化，投资者及上市公司为了自保及为了应对这种变化，中国股市新的乱象也自然产生。首先，中国股市这两天
页面全屏遮罩的实现方式 Rainbow702 html css 遮罩 mask
之前做了一个页面，在点击了某个按钮之后，要求页面出现一个全屏遮罩，一开始使用了position:absolute来实现的。当时因为画面大小是固定的，不可以resize的，所以，没有发现问题。最近用了同样的做法做了一个遮罩，但是画面是可以进行resize的，所以就发现了一个问题，当画面被reisze到浏览器出现了滚动条的时候，就发现，用absolute 的做法是有问题的。后来改成fixed定位就
关于angularjs的点滴 tntxia AngularJS
angular是一个新兴的JS框架，和以往的框架不同的事，Angularjs更注重于js的建模，管理，同时也提供大量的组件帮助用户组建商业化程序，是一种值得研究的JS框架。 Angularjs使我们可以使用MVC的模式来写JS。Angularjs现在由谷歌来维护。这里我们来简单的探讨一下它的应用。首先使用Angularjs我
Nutz--->>反复新建ioc容器的后果 xiaoxiao1992428 DAO mvc IOC nutz
问题： public class DaoZ { public static Dao dao() { // 每当需要使用dao的时候就取一次 Ioc ioc = new NutIoc(new JsonLoader("dao.js")); return ioc.get(

《统计学习方法》学习笔记之第一章

第一节 统计学习的定义与分类

统计学习的概念

统计学习的分类

第二节 统计学习方法的基本分类

监督学习

无监督学习

强化学习

第三节 统计学习方法三要素

模型

策略

第四节 模型评估与模型选择

训练误差与测试误差

过拟合与模型选择

第五节 正则化和交叉验证

正则化：实现结构风险最小化策略

交叉验证

第六节 泛化能力

泛化误差

泛化误差上界

二分类问题

第七节 生成模型与判别模型

生成模型和判别模型

生成模型VS判别模型

第八节 监督学习的应用

分类问题

标注问题

回归问题

你可能感兴趣的:(机器学习,机器学习,算法,线性回归)

第一节统计学习的定义与分类

第二节统计学习方法的基本分类

第三节统计学习方法三要素

第四节模型评估与模型选择

第五节正则化和交叉验证

第六节泛化能力

第七节生成模型与判别模型

第八节监督学习的应用