leetcode图论刷题总结

理论

1. 基本概念

1.1 顶点

图中的数据元素，我们称之为顶点，图至少有一个顶点（非空有穷集合）

1.2 边

顶点之间的关系用边表示。

1.3 度

度表示一个顶点包含多少条边，在有向图中，还分为出度和入度，出度表示从该顶点出去的边的条数，入度表示进入该顶点的边的条数。

1.4 无向图和有向图

边表示的是顶点之间的关系，有的关系是双向的，比如同学关系，A是B的同学，那么B也肯定是A的同学，那么在表示A和B的关系时，就不用关注方向，用不带箭头的边表示，这样的图就是无向图。有的关系是有方向的，比如父子关系，师生关系，微博的关注关系，A是B的爸爸，但B肯定不是A的爸爸，A关注B，B不一定关注A。在这种情况下，我们就用带箭头的边表示二者的关系，这样的图就是有向图。

1.5 无权图和带权图

对于一个关系，如果我们只关心关系的有无，而不关心关系有多强，那么就可以用无权图表示二者的关系。对于一个关系，如果我们既关心关系的有无，也关心关系的强度，比如描述地图上两个城市的关系，需要用到距离，那么就用带权图来表示，带权图中的每一条边一个数值表示权值，代表关系的强度。

2. 图的存储

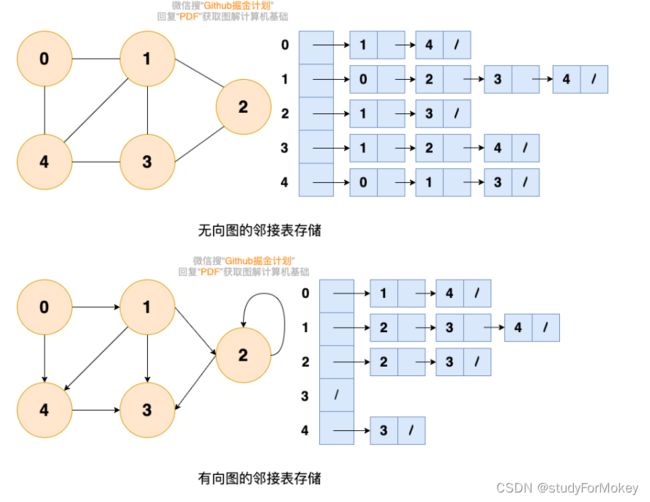
2.1 邻接矩阵存储

2.2 邻接表存储

3. 图的搜索

3.1 深度优先 DFS

深度优先搜索就是“一条路走到黑”，从源顶点开始，一直走到没有后继节点，才回溯到上一顶点，然后继续“一条路走到黑”

3.2 广度优先 BFS

广度优先搜索就像水面上的波纹一样一层一层向外扩展

T841. 钥匙和房间 (有向图找一条路径、DFS) **

• 思路分析
  有向图
  首先必须从0号房间开始搜索,一直搜，不需要回溯(只要找到一条路径就可以)，深度为len返回true

class Solution {
    //不需要回溯：只要找到一条符合的路径即可
    boolean[] visited;//记录是否访问过
    int deep;//记录访问深度
    public boolean canVisitAllRooms(List<List<Integer>> rooms) {
        int len = rooms.size();
        visited = new boolean[len];//false
        dfs(rooms,0);//从0号房间开始
        if(deep == len){return true;}
        return false;
    }
    public void dfs(List<List<Integer>> rooms,int index){
        visited[index] = true;
        deep++;//遍历依次深度就加1,由于设置的是没访问过的才会递归dfs,因此只要递归次数达到len,就说明满足条件
        for(int i:rooms.get(index)){//从该房间往可能的房间方向遍历
            if(visited[i]!=true){//访问的不需要再访问
                dfs(rooms,i);
            }
        }
    }
}

T797. 所有可能的路径(有向图找所有路径：DFS、回溯) **

所有路径需要回溯

class Solution {
    List<List<Integer>> res = new ArrayList<>();
    LinkedList<Integer> path = new LinkedList<>();
    public List<List<Integer>> allPathsSourceTarget(int[][] graph) {
        path.add(0);//0号房间需要手动加进去
        dfs(graph,0);
        return res;
    }
    public void dfs(int[][] graph, int index){
        //终止条件
        if(index == graph.length-1){//审题:终点必然是n-1
            res.add(new ArrayList<>(path));
            return;
        }
        for(int i=0;i<graph[index].length;i++){//遍历graph每个元素
            path.add(graph[index][i]);
            dfs(graph,graph[index][i]);
            path.removeLast();//回溯
        }
        return;
    }
}

T127. 单词接龙 (无向图求最短路径、BFS) ***

• 思路分析
  
  简历单词之间的联系
  广度优先搜索找到的必然是最短路径

class Solution {
    public int ladderLength(String beginWord, String endWord, List<String> wordList) {
        HashSet<String> wordSet = new HashSet<>(wordList);//把wordlist的单词放入hash表中
        if(!wordSet.contains(endWord)){return 0;}//特殊情况:不存在目标单词
        Queue<String> que = new LinkedList<>();
        que.offer(beginWord);
        Map<String,Integer> map = new HashMap<>();//单词:路径长度
        map.put(beginWord,1);

        while(!que.isEmpty()){
            String word = que.poll();
            int path = map.get(word);//取出第一个单词和其路径长度
            //对单词的每个字符进行修改遍历
            for(int i=0;i<word.length();i++){
                //修改字符
                char[] chars = word.toCharArray();
                for(char c='a';c<='z';c++){
                    chars[i] = c;
                    String newWord = String.valueOf(chars);//char变成string
                    if(newWord.equals(endWord)){
                        return path+1;//如果新单词与目标一致,返回结果
                    }
                    if(wordSet.contains(newWord) && !map.containsKey(newWord)){//存在该单词,且未使用过
                        map.put(newWord,path+1);
                        que.offer(newWord);
                    }
                }
            }
        }
        return 0;
    }

}

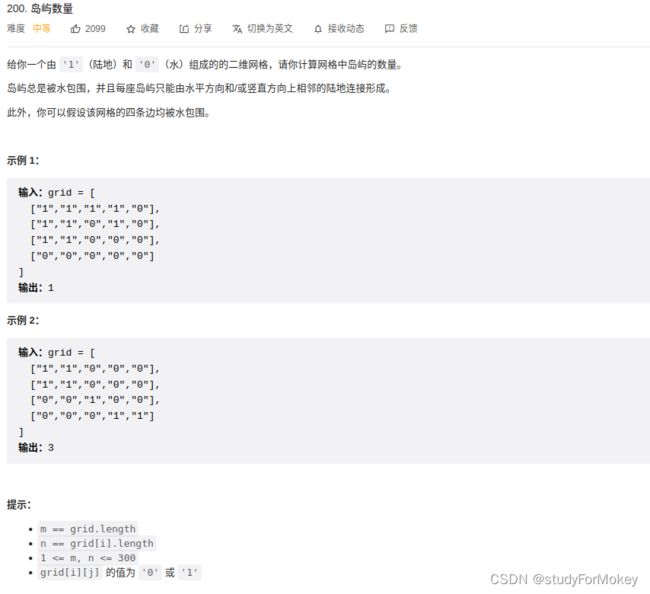
T200. 岛屿数量（无向图:DFS/BFS）*

- 思路分析
遇到陆地就开始向四个方向搜索，直到遇到海洋就停止，搜索过的就做个标记；
岛屿数量就是dfs了多少次

class Solution {
    public int numIslands(char[][] grid) {
        int count = 0;
        for(int m=0;m<grid.length;m++){
            for(int n=0;n<grid[0].length;n++){
                if(grid[m][n] == '1'){
                    dfs(grid,m,n);
                    count++;
                }
            }
        }
        return count;
    }
    void dfs(char[][] grid,int r,int c){
        //判断是否在表格中
        if(r<0||c<0||r>=grid.length||c>=grid[0].length){
            return;
        }
        //遇到非岛屿的
        if(grid[r][c] != '1') return;
        //记录遍历过的
        grid[r][c] = '2';
        //遍历四个方向
        dfs(grid,r-1,c);
        dfs(grid,r+1,c);
        dfs(grid,r,c-1);
        dfs(grid,r,c+1);
    }
}

class Solution {
    public int numIslands(char[][] grid) {
        int count = 0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j] == '1'){
                    bfs(grid,i,j);
                    count++;
                }
            }
        }
        return count;
    }
    public void bfs(char[][] grid,int i,int j){
        Queue<int[]> que = new LinkedList<>();
        que.offer(new int[]{i,j});
        while(!que.isEmpty()){
            int[] temp = que.poll();
            i = temp[0];
            j = temp[1];
            if(i>=0&&i<grid.length&&j>=0&&j<grid[0].length && grid[i][j] == '1'){
                grid[i][j] = '0';
                bfs(grid,i+1,j);
                bfs(grid,i-1,j);
                bfs(grid,i,j+1);
                bfs(grid,i,j-1);
            }
        }
    }
}

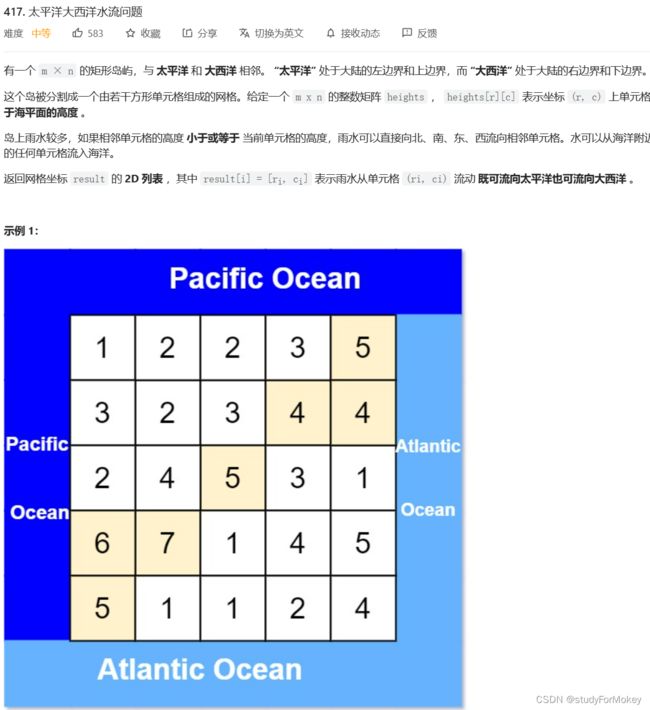
T417. 太平洋大西洋水流问题(无向图:多源BFS)****

• 思路分析
  题目翻译: 某个点出发，能从四个方向到达比它小的点，求整个集合中能够到达左上边界(太平洋) 右下边界(大西洋)的有哪些点
  思路解决: 遍历所有点太麻烦，直接从边界点出发,能够到达比它大的点，能够到达的就标记为true；分别从太平洋和大西洋出发，进行两次bfs，最终看结果res中两次标记为true的点就是所求。
  从结果开始遍历！
  BFS思路：以队列为基础，队列存放点坐标。传入点坐标，只要队列非空，就取点坐标，进行四个方向移动，更新，符合条件的入队。
• 代码实现

class Solution {
    static int[][] dirs = {{-1,0},{1,0},{0,-1},{0,1}};//移动的四个方向
    static int m;
    static int n;
    static int[][] nums;
    //反向推导:从边界出发，水往高处流，能到达就记为true
    public List<List<Integer>> pacificAtlantic(int[][] heights) {
        m = heights.length;
        n = heights[0].length;//行和列
        nums = heights;
        boolean[][] pacific = new boolean[m][n];//能否到达太平洋
        boolean[][] atlantic = new boolean[m][n];//记录能否到达大西洋
        //记录能否到达太平洋
        for(int i=0;i<m;i++){
            bfs(i,0,pacific);
        }
        for(int j=1;j<n;j++){
            bfs(0,j,pacific);
        }
        //记录能否到达大西洋
        for(int i=0;i<m;i++){
            bfs(i,n-1,atlantic);
        }
        for(int j=0;j<n-1;j++){
            bfs(m-1,j,atlantic);
        }
        //算结果:遍历所有的节点,能够同时到达太平洋和大西洋的就add
        List<List<Integer>> res = new ArrayList<>();
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(pacific[i][j] && atlantic[i][j]){
                    List<Integer> path = new ArrayList<>();
                    path.add(i);
                    path.add(j);
                    res.add(path);
                }
            }
        }
        return res;
    }
    //广度优先搜索的逻辑
    //取出其中一个点
    //往四个方向移动,判断条件是否符合
    //入队
    public static void bfs(int row,int col,boolean[][] ocean){
        if(ocean[row][col]){return;}
        ocean[row][col] = true;
        Queue<int[]> que = new LinkedList<>();//x,y坐标
        que.offer(new int[]{row,col});
        while(!que.isEmpty()){
            int[] temp = que.poll();
            for(int[] dir:dirs){//往四个方向移动
                //计算新坐标
                int newRow = temp[0] + dir[0];
                int newCol = temp[1] + dir[1];
                //判断是否符合条件:边界条件+高度+未处理过
                if(newRow>=0&&newRow<m&&newCol>=0&&newCol<n&& nums[temp[0]][temp[1]]<=nums[newRow][newCol]&& !ocean[newRow][newCol]){
                    ocean[newRow][newCol] = true;
                    que.offer(new int[]{newRow,newCol});
                }
            }
        }
    }
}

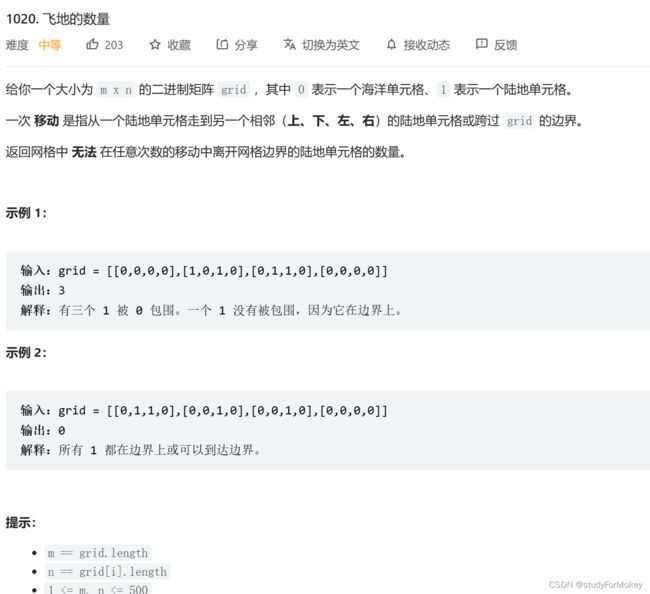
T1020. 飞地的数量 (无向图:DFS/多源BFS) ***

• 解法1：DFS搜索

class Solution {
    //从边界搜，如果遇到1，就设置为true;最终grid==1，false的就是飞地
    public static int[][] dirs = {{-1,0},{1,0},{0,-1},{0,1}};
    public static int m,n;
    public static boolean[][] visited;
    public int numEnclaves(int[][] grid) {
        int count = 0;
        m = grid.length;
        n = grid[0].length;
        visited = new boolean[m][n];
        //从边界开始搜
        //左右两个边界
        for(int i=0;i<m;i++){
            dfs(grid,i,0);
            dfs(grid,i,n-1);
        }
        //上下两个边界
        for(int j=0;j<n;j++){
            dfs(grid,0,j);
            dfs(grid,m-1,j);
        }
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(!visited[i][j] && grid[i][j]==1){
                    count++;
                }
            }
        }
        return count;
    }
    public static void dfs(int[][] grid,int i,int j){
        if(i<0 || i>=m || j<0 || j>=n || grid[i][j] == 0 || visited[i][j] ){
            return;//终止条件
        }
        visited[i][j] = true;
        for(int[] dir:dirs){
            dfs(grid,i+dir[0],j+dir[1]);
        }
    }
}

• 解法2：多源BFS

class Solution {
    //从边界搜，如果遇到1，就设置为true;最终grid==1，false的就是飞地
    public static int[][] dirs = {{-1,0},{1,0},{0,-1},{0,1}};
    public static int m,n;
    public static boolean[][] visited;
    public int numEnclaves(int[][] grid) {
        int count = 0;
        m = grid.length;
        n = grid[0].length;
        visited = new boolean[m][n];
        Queue<int[]> que = new LinkedList<>();

        //从边界开始搜
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(i==0||i==m-1||j==0||j==n-1){
                    if(grid[i][j]==0) continue;
                    visited[i][j] = true;
                    que.offer(new int[]{i,j});
                }
            }
        }
        while(!que.isEmpty()){
            int[] temp = que.poll();
            for(int[] dir:dirs){
                int newX = temp[0] + dir[0];
                int newY = temp[1] + dir[1];
                if(newX>=0 && newX<m && newY>=0 && newY<n && !visited[newX][newY] && grid[newX][newY]==1){
                    visited[newX][newY] = true;
                    que.offer(new int[]{newX,newY});
                }
            }
        }
        for(int i=0;i<m;i++){
            for(int j=0;j<n;j++){
                if(!visited[i][j] && grid[i][j]==1){
                    count++;
                }
            }
        }
        return count;
    }

}

剑指 Offer II 105. 岛屿的最大面积(无向图:DFS) **

在岛屿数量题目基础上，dfs递归函数返回岛屿面积的大小

class Solution {
    public int maxAreaOfIsland(int[][] grid) {
        int res  = 0;
        for(int i=0;i<grid.length;i++){
            for(int j=0;j<grid[0].length;j++){
                if(grid[i][j] == 1){
                    res = Math.max(dfs(grid,i,j),res);
                }
            }
        }
        return res;
    }
    public int dfs(int[][] grid,int row,int col){
        if(row<0 || col<0 || row>=grid.length || col >= grid[0].length||grid[row][col]!=1){
            return 0;
        }
        grid[row][col] = 0;
        int res = 1;
        res = res + dfs(grid,row+1,col) + dfs(grid,row-1,col) +
            dfs(grid,row,col+1) + dfs(grid,row,col-1);
        return res;

    }
}

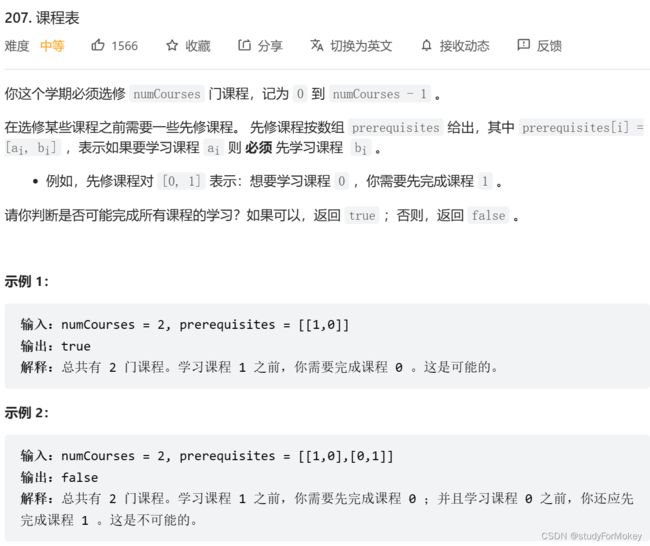
T207. 课程表(拓扑排序判断是否为有向无环图：邻接表+BFS)

• 入度表BFS

class Solution {
    //BFS 构造一个有向图
    //1.统计每个点的入度
    //2.度为0的入队
    //3.出队:课程数-1,相连的节点的度减去1,若度为0就入度
    public boolean canFinish(int numCourses, int[][] prerequisites) {
        int[] indegree = new int[numCourses];//统计入度
        List<List<Integer>> joinList = new ArrayList<>();//记录相连的课程,索引代表当前课程
        for(int i=0;i<numCourses;i++){
            joinList.add(new ArrayList<>());
        }
        for(int[] item:prerequisites){
            indegree[item[0]]++;//入度数
            joinList.get(item[1]).add(item[0]);//相连的节点
        }
        Queue<Integer> que = new LinkedList<>();
        for(int i=0;i<indegree.length;i++){
            if(indegree[i]==0){
                que.add(i);//度为0 入队
            }
        }
        while(!que.isEmpty()){
            int temp = que.poll();
            numCourses--;
            for(int item:joinList.get(temp)){
                indegree[item]--;
                if(indegree[item]==0){
                    que.add(item);
                }
            }
        }
        return numCourses==0;
    }
}

T684. 冗余连接（无向图中找环：邻接表BFS/并查集）

• 解法1：邻接表，入度表，BFS

参考题：课程表，不同的是度数为1入队。每次把1的出队，并且删除掉与其相连的边，最终剩下的结果中，两边入度都大于1的为所求

class Solution {
    public int[] findRedundantConnection(int[][] edges) {
        int size = edges.length;
        int[] indegree = new int[size];//构造入度表 下标0表示1
        List<List<Integer>> joinList = new ArrayList<>();//邻接表
        for(int i=0;i<size;i++){
            joinList.add(new ArrayList<>());
        }
        for(int[] item:edges){//下标统一做减1处理
            indegree[item[0]-1]++;
            indegree[item[1]-1]++;
            joinList.get(item[0]-1).add(item[1]-1);
            joinList.get(item[1]-1).add(item[0]-1);
        }
        Queue<Integer> que = new LinkedList<>();
        for(int i=0;i<size;i++){
            if(indegree[i]==1){
                que.offer(i);//度为1 就入队
            }
        }
        while(!que.isEmpty()){
            int item = que.poll();
            for(int i:joinList.get(item)){
                indegree[i]--;
                if(indegree[i]==1){
                    que.offer(i);
                }
            }
        }
        //前边是找环的思路 同题 课程表
        //从后往前遍历:如果两个相连的点度数都大于1
        for(int i=size-1;i>=0;i--){
            if(indegree[edges[i][0]-1]>1&&indegree[edges[i][1]-1]>1){
                return edges[i];
            }
        }
        return new int[0];
    }
}

华为机考题:循环依赖(有向图中找环并输出节点)

为了方便对原题修改了一下
//输入:
8 （模块名称：模块里的函数）
A a1 a2 a3
B b1 b2 b3
C c1 c2 c3
D d1 d2 d3
E e1 e2 e3
F f1 f2 f3
H h1 h2
G g1 g2 g3
5 (主函数：需要用到的函数，即a1依赖b1,b2)
a1 b1 b2
c2 a3
d2 e1
e1 b1 f2 g3
b2 b1 c2 d1 h1
//输出:
A B C D E

package HuaWei;
/**
 * 循环依赖 思路不算难 但是过程很繁琐 java构建输入太过于复杂
 * 考察的是：在一个有向图中找环，并输出环的节点。
 * 解决方法：构建一个邻接表，利用dfs搜索，用res记录路径
 * https://blog.csdn.net/zhilamou7549/article/details/107092998思路见此
 * 为了简化，此题不再做起点要求,对整个图进行搜索找环，并且规定起始点为A
 */

import java.util.*;

public class Solution7 {
    static List<List<String>> res = new ArrayList<>();
    static List<String> path = new LinkedList<>();
    static String[]  numToStr;
    static boolean result;
    public static void main(String[] args) {
        Scanner sc = new Scanner(System.in);
        int m = Integer.parseInt(sc.nextLine());
        numToStr = new String[m];
        int tempSize = m;
        int index = 0;
        TreeMap<String,List<String>> map = new TreeMap<>();//模块以及其对应的函数
        while(m>0){
            String[] line = sc.nextLine().split(" ");
            numToStr[index] = line[0];
            index++;
            List<String> list = new LinkedList<>();
            for(int i=1;i<line.length;i++){
                list.add(line[i]);
            }
            map.put(line[0],list);//模块名:对应函数的名字
            m--;
        }
        int n = Integer.parseInt(sc.nextLine());
        TreeMap<String,Set<String>> relation = new TreeMap<>();//各个模块之间的依赖关系
        while(n>0) {
            String[] parts = sc.nextLine().split(" ");
            Set<String> value = new HashSet<>();
            String key = null;
            for (Map.Entry<String, List<String>> entry : map.entrySet()) {
                List<String> temp = entry.getValue();
                for (String str : temp) {
                    if (parts[0].equals(str)) {//找到和parts[0]对应的函数 对应的模块 作为key
                        key = entry.getKey();
                    }
                }
            }
            for (int i = 1; i < parts.length; i++) {//寻找value
                for (Map.Entry<String, List<String>> entry : map.entrySet()) {
                    List<String> temp = entry.getValue();
                    for (String str : temp) {
                        if (parts[i].equals(str)) {//找到和parts[0]对应的函数 对应的模块 作为key
                            if(!entry.getKey().equals(key)){
                                value.add(entry.getKey());//给value赋值 记得去重
                            }
                        }
                    }
                }
            }
            relation.put(key, value);
            n--;
        }
//        System.out.println(map);
//        System.out.println(relation);
//        String target = sc.nextLine();//起点模块
        //处理逻辑:默认模块名从A开始排序了
        //1.构建邻接表
        //行表示当前模块,列表示对应模块，若行依赖于列，值为1
        
        int[][] matrix = new int[tempSize][tempSize];
        for(Map.Entry<String,Set<String>> entry: relation.entrySet()){
            int row = entry.getKey().charAt(0) - 'A';
            for(String str: entry.getValue()){
                int col = str.charAt(0) - 'A';
                matrix[row][col] = 1;
            }
        }
//        System.out.println(matrix);
        //2.dfs处理
        boolean[] visited = new boolean[matrix.length];
       for(int i=0;i<matrix.length;i++){
           for (int j = 0; j < matrix.length; j++) {
               //遇到值为1就进行搜索. 如果两次出现visited都为true说明出现了环
               if(matrix[i][j]!=0){
                   Arrays.fill(visited,false);
                   visited[j] = true;
                   dfs(matrix,visited,i,j);
               }
           }
       }
        if(result){
            System.out.println("yes");
            Set<String> set = new HashSet<>();
            for(List<String> list:res){
                for(String str:list){
                    set.add(str);
                }
            }
            String[] strResult = new String[set.size()];
            int i = 0;
            for(String str:set){
                strResult[i] = str;
                i++;
            }
            Arrays.sort(strResult);
            for(int j=0;j<strResult.length;j++){
                System.out.print(strResult[j]+" ");
            }
        }else{
            System.out.println("No!");
        }
//        System.out.println(res);

    }
    public static void dfs(int[][] matrix,boolean[] visited,int start,int cur_node){
        for(int col=0;col<matrix.length;col++){
            if(matrix[cur_node][col]!=0&&!visited[col]){
                if(col == start){//找到环了
                    res.add(new ArrayList<>(path));
                    result = true;
                    return;
                }
                visited[col] = true;
                path.add(numToStr[col]);
                dfs(matrix,visited,start,col);
                visited[col] = false;
                path.remove(numToStr[col]);
            }
        }
    }
}

T130. 被围绕的区域