matlab数学建模方法与实践 笔记汇总
matlab数学建模方法与实践 笔记汇总
- 写在最前面
- 笔记1:快速入门
-
- 1.导入数据
- 2.数据探索
- 3.多项式拟合
- 4.发布功能
- 5.数据类型
- 6、全部代码
- 笔记2:数据的准备
-
- 1.数据的读取与写入
-
- excel、txt
- 读图
- 读视频
- 2.数据预处理
-
- 缺失值
- 噪声过滤
- 数据归约
- 数据变换
- 3.数据统计
- 4.数据可视化
-
- P431.m
- 柱状分布图
- 常见统计量绘制于分布图中
- 数据关联
- 箱型图
- 5.数据降维
-
- PCA
- 笔记3:常用数学建模方法
-
- 1.一元回归
-
- 一元线性回归
- 一元非线性回归
- 2.多元回归
- 3.逐步回归
- 4.logistic回归
- 笔记4:机器学习
-
- 1.概述
- 2.分类
-
- K-NN算法
- 朴素贝叶斯
- 支持向量机SVM
- 聚类
-
- K-means
- 层次聚类+FCM
- 深度学习
- 笔记5:其他建模方法
-
- 1.灰色预测
- 2.小波去噪
写在最前面
快速从零入门matlab数学建模,从数据预览(绘制)、预处理、常用建模方法到机器学习、小波去噪等其他建模方法
注:为书的阅读笔记
《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
代码在Cha2文件夹下
笔记1:快速入门
1.导入数据
2.数据探索
3.多项式拟合
4.发布功能
5.数据类型
6、全部代码
% MATLAB 入门案例
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
%% 导入数据
clc, clear, close all
% 导入数据
[~, ~, raw] = xlsread('sz000004.xls','Sheet1','A2:H99');
% 创建输出变量
data = reshape([raw{:}],size(raw));
% 将导入的数组分配给列变量名称
Date = data(:,1);
DateNum = data(:,2);
Popen = data(:,3);
Phigh = data(:,4);
Plow = data(:,5);
Pclose = data(:,6);
Volum = data(:,7);
Turn = data(:,8);
% 清除临时变量
clearvars data raw;
%% 数据探索
figure % 创建一个新的图像窗口
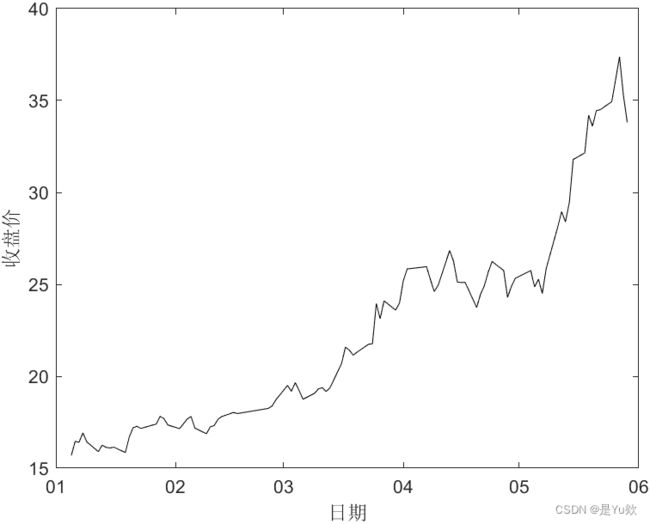
plot(DateNum,Pclose,'k') % 更改图的的颜色的黑色(打印后不失真)
datetick('x','mm');% 更白日期显示类型
xlabel('日期'); % x轴说明
ylabel('收盘价'); % y轴说明
figure
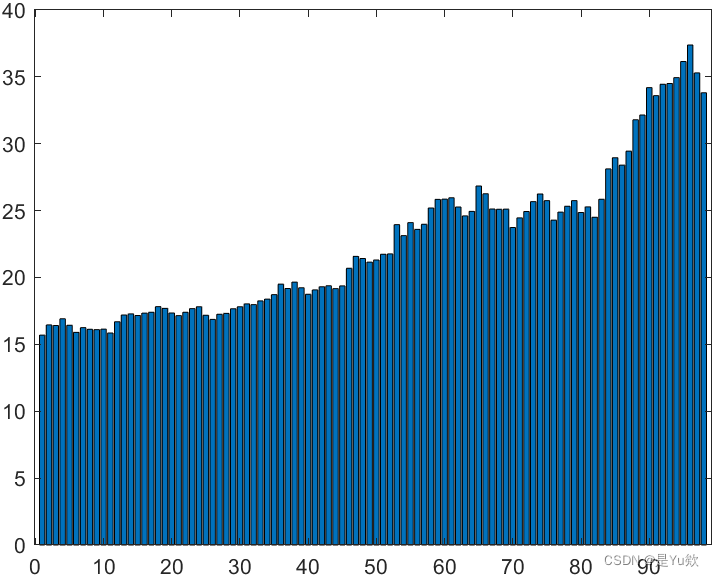
bar(Pclose) % 作为对照图形
%% 股票价值的评估
p = polyfit(DateNum,Pclose,1); % 多项式拟合,
% 分号作用为不在命令窗口显示执行结果
P1 = polyval(p,DateNum); % 得到多项式模型的结果
figure
plot(DateNum,P1,DateNum,Pclose,'*g'); % 模型与原始数据的对照
value = p(1) % 将斜率赋值给value, 作为股票的价值。
%% 股票风险的评估
MaxDD = maxdrawdown(Pclose); % 计算最大回撤
risk = MaxDD % 将最大回撤赋值给risk, 作为股票的风险
笔记2:数据的准备
1.数据的读取与写入
excel、txt
P23-25
读图
cha3
ReadImages
%% 读取图片
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
clc, clear, close all
a1=imread('000.bmp');
[m,n]=size(a1);
%% 批量读取图片
dirname = 'ImageChips';
files = dir(fullfile(dirname, '*.bmp'));
a=zeros(m,n,19);
pic=[];
for ii = 1:length(files)
filename = fullfile(dirname, files(ii).name);
a(:,:,ii)=imread(filename);
pic=[pic,a(:,:,ii)];
end
double(pic);
figure
imshow(pic,[])
此外参考https://blog.csdn.net/WTYuong/article/details/122626337
图像识别系列
读视频
选取某帧数图像进行图像层面的分析
cha3
readVideo
%% 读取视频数据
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
videoFReader = vision.VideoFileReader('vippedtracking.mp4');
% 播放视频文件
videoPlayer = vision.VideoPlayer;
while ~isDone(videoFReader)
videoFrame = step(videoFReader);
step(videoPlayer, videoFrame);
end
release(videoPlayer);
%% 设置播放方式
% 重置播放器
reset(videoFReader)
% 增加播放器的尺寸
r = groot;
scrPos = r.ScreenSize;
% Size/position is always a 4-element vector: [x0 y0 dx dy]
dx = scrPos(3); dy = scrPos(4);
videoPlayer = vision.VideoPlayer('Position',[dx/8, dy/8, dx*(3/4), dy*(3/4)]);
while ~isDone(videoFReader)
videoFrame = step(videoFReader);
step(videoPlayer, videoFrame);
end
release(videoPlayer);
reset(videoFReader)
%% 获取视频中的图像
videoFrame = step(videoFReader);
n = 0;
while n~=15
videoFrame = step(videoFReader);
n = n+1;
end
figure, imshow(videoFrame)
release(videoPlayer);
release(videoFReader)
2.数据预处理
P27
缺失值
删除、插补(均值、回归、极大似然估计(期望值最大化))
噪声过滤
回归、平滑、离群点分析、小波过滤
#3# 数据集成
建模比赛没有
数据归约
属性选择、样本选择
相关性分析、主成分分析
数据变换
P33
标准化、离散化、语义转换
3.数据统计
4.数据可视化
P431.m
柱状分布图
图3-8即为用hist绘制的变量的柱状分布图,该图的优势是更直观地反映了数据的集程序。由该图可以看出,变量dv3过于集中,这对数据建模是不利的,相当于这个变量基本是固定值,对任何样本都是一样的,所以没有区分效果,这样的变量就可以考虑删除了。可见数据进行可视化分析,意义还是很大的。
% 数据可视化——基本绘图
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
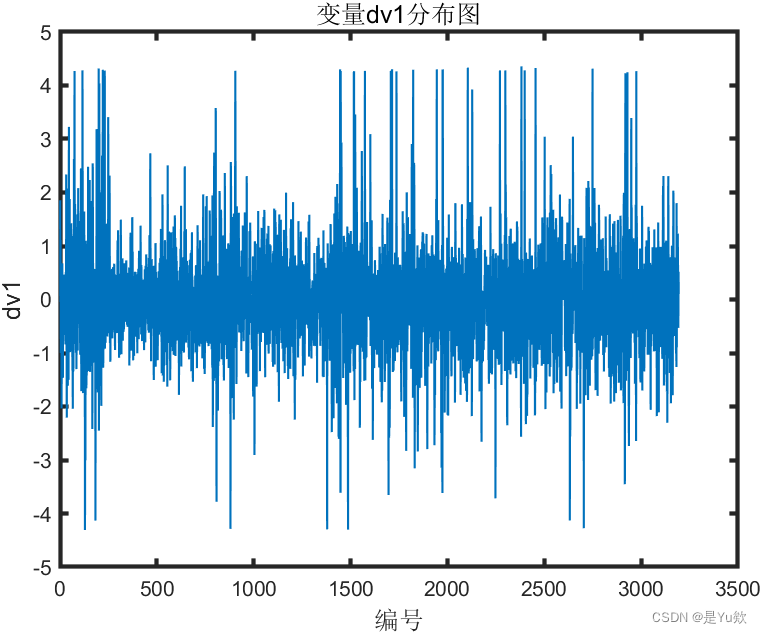
% 绘制变量dv1的基本分布
N=size(X,1);
id=1:N;
figure
plot( id', X(:,2),'LineWidth',1)
set(gca,'linewidth',2);
xlabel('编号','fontsize',12);
ylabel('dv1', 'fontsize',12);
title('变量dv1分布图','fontsize',12);
% 同时绘制变量dv1-dv4的柱状分布图
figure
subplot(2,2,1);
hist(X(:,2));
title('dv1柱状分布图','fontsize',12)
subplot(2,2,2);
hist(X(:,3));
title('dv2柱状分布图','fontsize',12)
subplot(2,2,3);
hist(X(:,4));
title('dv3柱状分布图','fontsize',12)
subplot(2,2,4);
hist(X(:,5));
title('dv4柱状分布图','fontsize',12)
常见统计量绘制于分布图中
% 数据可视化——数据分布形状图
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
dv1=X(:,2);
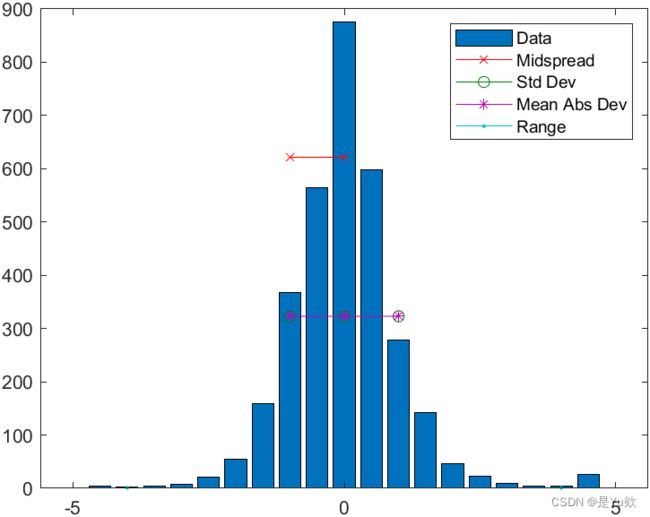
% 绘制变量dv1的柱状分布图
h = -5:0.5:5;
n = hist(dv1,h);
figure
bar(h, n)
% 计算常用的形状度量指标
mn = mean(dv1); % 均值
sdev = std(dv1); % 标准差
mdsprd = iqr(dv1); % 四分位数
mnad = mad(dv1); % 中位数
rng = range(dv1); % 极差
% 标识度量数值
x = round(quantile(dv1,[0.25,0.5,0.75]));
y = (n(h==x(1)) + n(h==x(3)))/2;
line(x,[y,y,y],'marker','x','color','r')
x = round(mn + sdev*[-1,0,1]);
y = (n(h==x(1)) + n(h==x(3)))/2;
line(x,[y,y,y],'marker','o','color',[0 0.5 0])
x = round(mn + mnad*[-1,0,1]);
y = (n(h==x(1)) + n(h==x(3)))/2;
line(x,[y,y,y],'marker','*','color',[0.75 0 0.75])
x = round([min(dv1),max(dv1)]);
line(x,[1,1],'marker','.','color',[0 0.75 0.75])
legend('Data','Midspread','Std Dev','Mean Abs Dev','Range')
数据关联
P433.m
% 数据可视化——变量想相关性
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
Vars = X(:,7:12);
% 绘制变量间相关性关联图
figure
plotmatrix(Vars)
% 绘制变量间相关性强度图
covmat = corrcoef(Vars);
figure
imagesc(covmat);
grid;
colorbar;
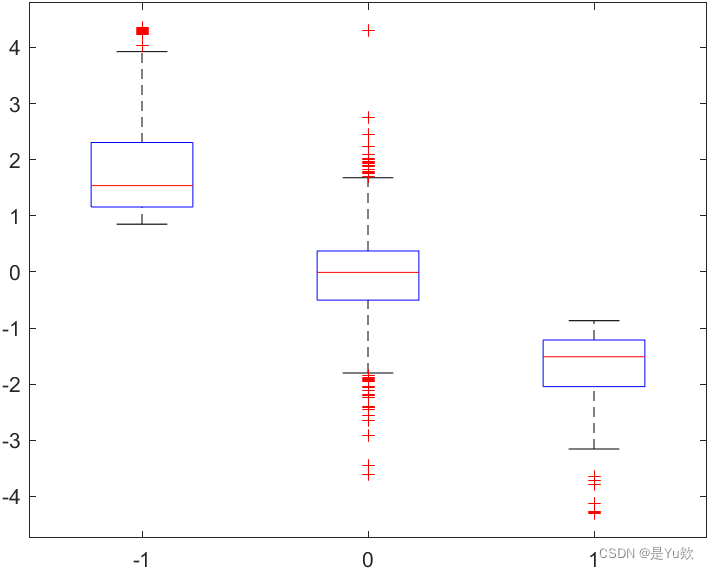
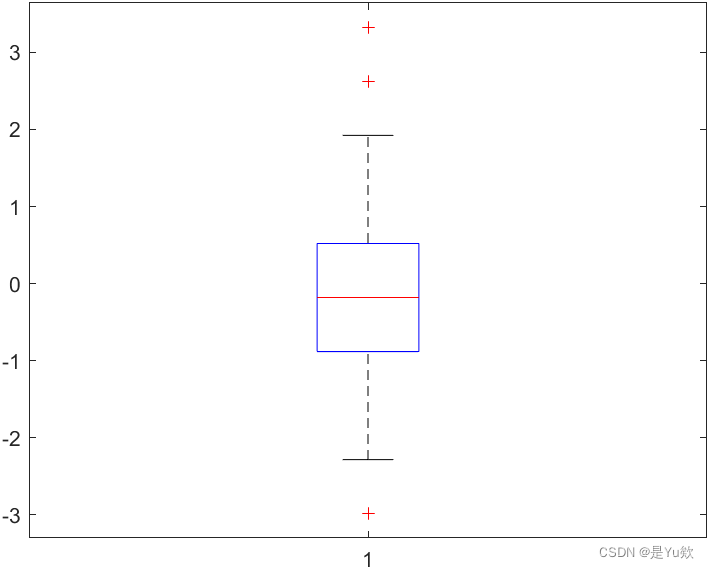
箱型图
% 数据可视化——数据分组
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
% 读取数据
clc, clear al, close all
X=xlsread('dataTableA2.xlsx');
dv1=X(:,2);
eva=X(:,12);
% Boxplot
figure
boxplot(X(:,2:12))
figure
boxplot(dv1, eva)
figure
boxplot(X(:,5))
5.数据降维
PCA
P41 原理、步骤
p43 案例
%% PCA数据降维实例
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
%% 读取数据
A=xlsread('Coporation_evaluation.xlsx', 'B2:I16');
% Transfer orginal data to standard data
a=size(A,1); % Get the row number of A
b=size(A,2); % Get the column number of A
for i=1:b
SA(:,i)=(A(:,i)-mean(A(:,i)))/std(A(:,i)); % Matrix normalization
end
% Calculate correlation matrix of A.
CM=corrcoef(SA);
% Calculate eigenvectors and eigenvalues of correlation matrix.
[V, D]=eig(CM);
% Get the eigenvalue sequence according to descending and the corrosponding
% attribution rates and accumulation rates.
for j=1:b
DS(j,1)=D(b+1-j, b+1-j);
end
for i=1:b
DS(i,2)=DS(i,1)/sum(DS(:,1));
DS(i,3)=sum(DS(1:i,1))/sum(DS(:,1));
end
% Calculate the numvber of principal components.
T=0.9; % set the threshold value for evaluating information preservation level.
for K=1:b
if DS(K,3)>=T
Com_num=K;
break;
end
end
% Get the eigenvectors of the Com_num principal components
for j=1:Com_num
PV(:,j)=V(:,b+1-j);
end
% Calculate the new socres of the orginal items
new_score=SA*PV;
for i=1:a
total_score(i,2)=sum(new_score(i,:));
total_score(i,1)=i;
end
new_score_s=sortrows(total_score,-2);
%% 显示结果
disp('特征值及贡献率:')
DS
disp('阀值T对应的主成分数与特征向量:')
Com_num
PV
disp('主成分分数:')
new_score
disp('主成分分数排序:')
new_score_s
笔记3:常用数学建模方法
1.一元回归
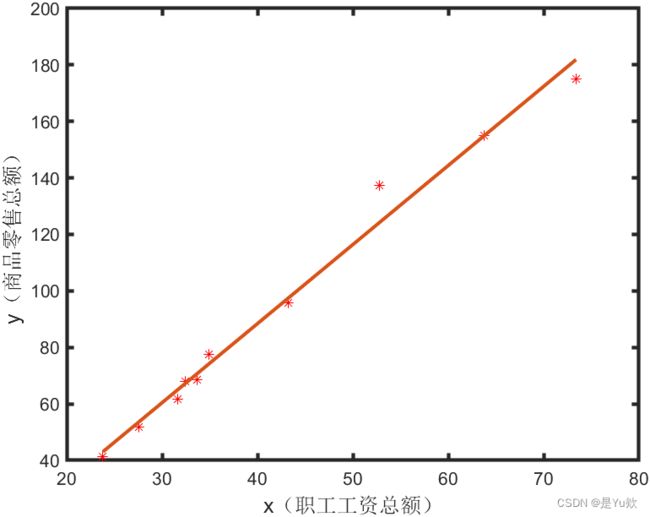
一元线性回归
%% 一元线性回归实例
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
%% 输入数据
clc, clear all, close all
x=[23.80,27.60,31.60,32.40,33.70,34.90,43.20,52.80,63.80,73.40];
y=[41.4,51.8,61.70,67.90,68.70,77.50,95.90,137.40,155.0,175.0];
%% 采用最小二乘回归
% 绘制散点图,判断是否具有线性关系
figure
plot(x,y,'r*') %作散点图
xlabel('x(职工工资总额)','fontsize', 12) %横坐标名
ylabel('y(商品零售总额)', 'fontsize',12) %纵坐标名
set(gca,'linewidth',2);
% 采用最小二乘拟合
Lxx=sum((x-mean(x)).^2);
Lxy=sum((x-mean(x)).*(y-mean(y)));
b1=Lxy/Lxx;
b0=mean(y)-b1*mean(x);
y1=b1*x+b0;
hold on
plot(x, y1,'linewidth',2);
%% 采用LinearModel.fit函数进行回归
m2 = LinearModel.fit(x,y)
%% 采用regress函数进行回归
Y=y';
X=[ones(size(x,2),1),x'];
[b, bint, r, rint, s] = regress(Y, X)
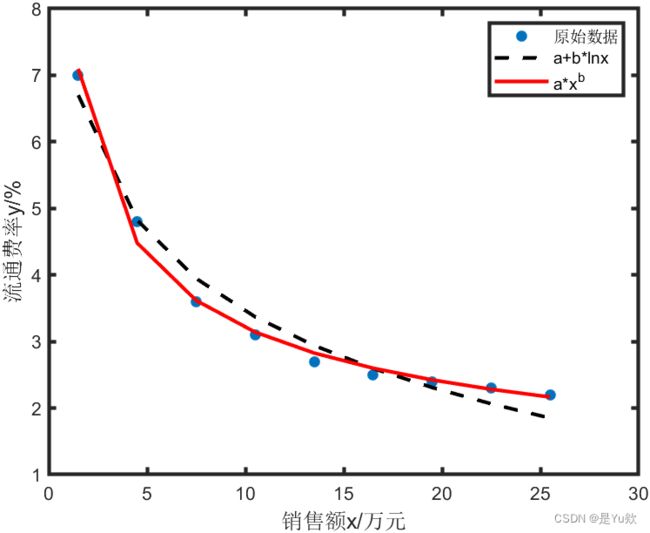
一元非线性回归
%% 一元非线性回归实例
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
%% 输入数据
clc, clear all, close all
x=[1.5, 4.5, 7.5,10.5,13.5,16.5,19.5,22.5,25.5];
y=[7.0,4.8,3.6,3.1,2.7,2.5,2.4,2.3,2.2];
plot(x,y,'*','linewidth',2);
set(gca,'linewidth',2);
xlabel('销售额x/万元','fontsize', 12)
ylabel('流通费率y/%', 'fontsize',12)
%% 对数形式
m1 = @(b,x) b(1) + b(2)*log(x);
nonlinfit1 = fitnlm(x,y,m1,[0.01;0.01])
b=nonlinfit1.Coefficients.Estimate;
Y1=b(1,1)+b(2,1)*log(x);
hold on
plot(x,Y1,'--k','linewidth',2)
%% 指数形式拟合
m2 = 'y ~ b1*x^b2';
nonlinfit2 = fitnlm(x,y,m2,[1;1])
b1=nonlinfit2.Coefficients.Estimate(1,1);
b2=nonlinfit2.Coefficients.Estimate(2,1);
Y2=b1*x.^b2;
hold on
plot(x,Y2,'r','linewidth',2)
legend('原始数据','a+b*lnx','a*x^b')
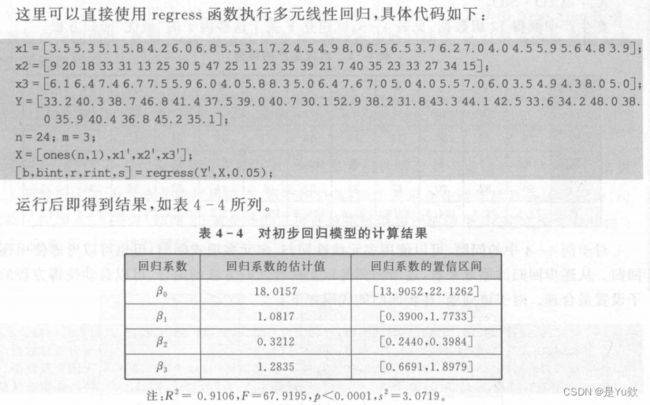
2.多元回归
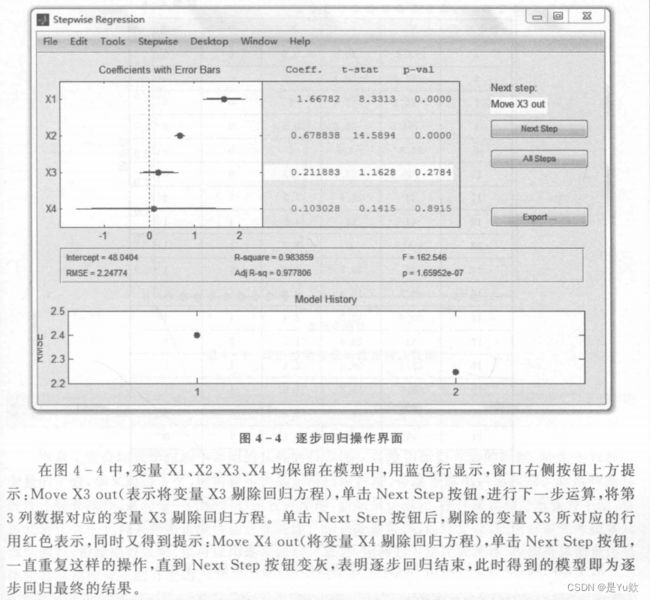
3.逐步回归
4.logistic回归
回归系数:-0.63656 0.004127 0.016292 0.53305
评价结果:0 0 0 0 0 0 0 0 0 0 1 1 1 1 1 1 1 1 1 1 0 0 1 1 1
笔记4:机器学习
1.概述
2.分类
%% svm高版本
% classifier = fitcsvm(train_data,train_labels,'KernelFunction','linear')
% test_labels = predict(classifier, test_data);
%%
%% 贝叶斯分类高版本
% 使用该工具箱重新整合代码 fitcnb
% 具体使用方式 在命令行输入 doc fitcnb
%%
%% 分类方法示例程序
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
clc, clear all, close all
%% 导入数据及数据预处理
load bank.mat
% 将分类变量转换成分类数组
names = bank.Properties.VariableNames;
category = varfun(@iscellstr, bank, 'Output', 'uniform');
for i = find(category)
bank.(names{i}) = categorical(bank.(names{i}));
end
% 跟踪分类变量
catPred = category(1:end-1);
% 设置默认随机数生成方式确保该脚本中的结果是可以重现的
rng('default');
% 数据探索----数据可视化
figure(1)
gscatter(bank.balance,bank.duration,bank.y,'kk','xo')
xlabel('年平均余额/万元', 'fontsize',12)
ylabel('上次接触时间/秒', 'fontsize',12)
title('数据可视化效果图', 'fontsize',12)
set(gca,'linewidth',2);
% 设置响应变量和预测变量
X = table2array(varfun(@double, bank(:,1:end-1))); % 预测变量
Y = bank.y; % 响应变量
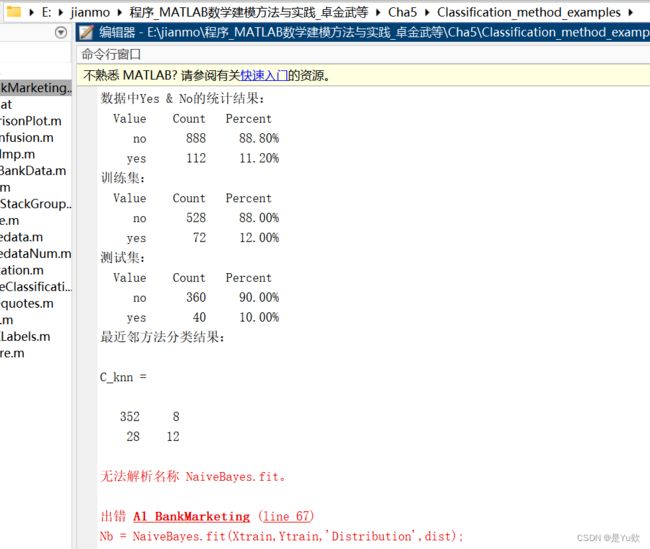
disp('数据中Yes & No的统计结果:')
tabulate(Y)
%将分类数组进一步转换成二进制数组以便于某些算法对分类变量的处理
XNum = [X(:,~catPred) dummyvar(X(:,catPred))];
YNum = double(Y)-1;
%% 设置交叉验证方式
% 随机选择40%的样本作为测试样本
cv = cvpartition(height(bank),'holdout',0.40);
% 训练集
Xtrain = X(training(cv),:);
Ytrain = Y(training(cv),:);
XtrainNum = XNum(training(cv),:);
YtrainNum = YNum(training(cv),:);
% 测试集
Xtest = X(test(cv),:);
Ytest = Y(test(cv),:);
XtestNum = XNum(test(cv),:);
YtestNum = YNum(test(cv),:);
disp('训练集:')
tabulate(Ytrain)
disp('测试集:')
tabulate(Ytest)
%% 最近邻
% 训练分类器
knn = ClassificationKNN.fit(Xtrain,Ytrain,'Distance','seuclidean',...
'NumNeighbors',5);
% 进行预测
[Y_knn, Yscore_knn] = knn.predict(Xtest);
Yscore_knn = Yscore_knn(:,2);
% 计算混淆矩阵
disp('最近邻方法分类结果:')
C_knn = confusionmat(Ytest,Y_knn)
% %% 贝叶斯
% % 设置分布类型
% dist = repmat({'normal'},1,width(bank)-1);
% dist(catPred) = {'mvmn'};
% % 训练分类器
% Nb = fitcnb(Xtrain,Ytrain);
% % 进行预测
% Y_Nb = Nb.predict(Xtest);
% Yscore_Nb = Nb.posterior(Xtest);
% Yscore_Nb = Yscore_Nb(:,2);
% % 计算混淆矩阵
% disp('贝叶斯方法分类结果:')
% C_nb = confusionmat(Ytest,Y_Nb)
%% 神经网络
% 设置神经网络模式及参数
hiddenLayerSize = 5;
net = patternnet(hiddenLayerSize);
% 设置训练集、验证机和测试集
net.divideParam.trainRatio = 70/100;
net.divideParam.valRatio = 15/100;
net.divideParam.testRatio = 15/100;
% 训练网络
net.trainParam.showWindow = false;
inputs = XtrainNum';
targets = YtrainNum';
[net,~] = train(net,inputs,targets);
% 用测试集数据进行预测
Yscore_nn = net(XtestNum')';
Y_nn = round(Yscore_nn);
% 计算混淆矩阵
disp('神经网络方法分类结果:')
C_nn = confusionmat(YtestNum,Y_nn)
%% Logistic
% 训练分类器
glm = fitglm(Xtrain,YtrainNum,'linear', 'Distribution','binomial',...
'link','logit','CategoricalVars',catPred, 'VarNames', names);
% 用测试集数据进行预测
Yscore_glm = glm.predict(Xtest);
Y_glm = round(Yscore_glm);
% 计算混淆矩阵
disp('Logistic方法分类结果:')
C_glm = confusionmat(YtestNum,Y_glm)
%% 判别分析
% 训练分类器
da = ClassificationDiscriminant.fit(XtrainNum,Ytrain);
% 进行预测
[Y_da, Yscore_da] = da.predict(XtestNum);
Yscore_da = Yscore_da(:,2);
% 计算混淆矩阵
disp('判别方法分类结果:')
C_da = confusionmat(Ytest,Y_da)
%% 支持向量机(SVM)
% 设置最大迭代次数
opts = statset('MaxIter',45000);
% 训练分类器
svmStruct = svmtrain(Xtrain,Ytrain,'kernel_function','linear','kktviolationlevel',0.2,'options',opts);
% 进行预测
Y_svm = svmclassify(svmStruct,Xtest);
Yscore_svm = svmscore(svmStruct, Xtest);
Yscore_svm = (Yscore_svm - min(Yscore_svm))/range(Yscore_svm);
% 计算混淆矩阵
disp('SVM方法分类结果:')
C_svm = confusionmat(Ytest,Y_svm)
%% 决策树
% 训练分类器
t = ClassificationTree.fit(Xtrain,Ytrain,'CategoricalPredictors',catPred);
% 进行预测
Y_t = t.predict(Xtest);
% 计算混淆矩阵
disp('决策树方法分类结果:')
C_t = confusionmat(Ytest,Y_t)
%% 通过ROC曲线来比较方法
methods = {'KNN','NBayes','NNet', 'GLM', 'LDA', 'SVM'};
scores = [Yscore_knn, Yscore_Nb, Yscore_nn, Yscore_glm, Yscore_da, Yscore_svm];
%绘制ROC曲线
figure
auc= zeros(6); hCurve = zeros(1,6);
for ii=1:6;
[rocx, rocy, ~, auc(ii)] = perfcurve(Ytest, scores(:,ii), 'yes');
hCurve(ii,:) = plot(rocx, rocy, 'k','LineWidth',2); hold on;
end
legend(hCurve(:,1), methods)
set(gca,'linewidth',2);
grid on;
title('各方法ROC曲线', 'fontsize',12);
xlabel('假阳率 [ = FP/(TN+FP)]', 'fontsize',12);
ylabel('真阳率 [ = TP/(TP+FN)]', 'fontsize',12);
% 绘制各方法分类正确率
figure;
bar(auc); set(gca,'YGrid', 'on','XTickLabel',methods);
xlabel('方法简称', 'fontsize',12);
ylabel('分类正确率', 'fontsize',12);
title('各方法分类正确率','fontsize',12);
set(gca,'linewidth',2);
K-NN算法
朴素贝叶斯
P66
2019b跑不通,报错
无法解析名称 NaiveBayes.fit。
根据网上经验贴修改后报另一个无法解决的报错,因而暂放
支持向量机SVM
报错
尝试安装 lib-svm
未果
聚类
K-means
同型相关系数: 0.8804
层次聚类+FCM
深度学习
笔记5:其他建模方法
1.灰色预测
% 灰色预测
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
clear
syms a b;
c=[a b]';
A=[89677,99215,109655,120333,135823,159878,182321,209407,246619,300670];
B=cumsum(A); % 原始数据累加
n=length(A);
for i=1:(n-1)
C(i)=(B(i)+B(i+1))/2; % 生成累加矩阵
end
% 计算待定参数的值
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
% 预测后续数据
F=[];F(1)=A(1);
for i=2:(n+10)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a ;
end
G=[];G(1)=A(1);
for i=2:(n+10)
G(i)=F(i)-F(i-1); %得到预测出来的数据
end
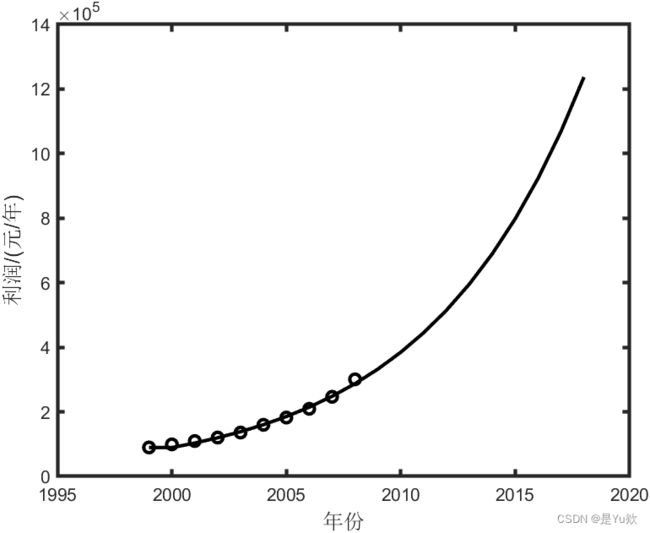
t1=1999:2008;
t2=1999:2018;
G
plot(t1,A,'ko', 'LineWidth',2)
hold on
plot(t2,G,'k', 'LineWidth',2)
xlabel('年份', 'fontsize',12)
ylabel('利润/(元/年)','fontsize',12)
set(gca, 'LineWidth',2);
% 灰色预测
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
clear
syms a b;
c=[a b]';
A=[174 179 183 189 207 234 220.5 256 270 285];
B=cumsum(A); % 原始数据累加
n=length(A);
for i=1:(n-1)
C(i)=(B(i)+B(i+1))/2; % 生成累加矩阵
end
% 计算待定参数的值
D=A;D(1)=[];
D=D';
E=[-C;ones(1,n-1)];
c=inv(E*E')*E*D;
c=c';
a=c(1);b=c(2);
% 预测后续数据
F=[];F(1)=A(1);
for i=2:(n+10)
F(i)=(A(1)-b/a)/exp(a*(i-1))+b/a ;
end
G=[];G(1)=A(1);
for i=2:(n+10)
G(i)=F(i)-F(i-1); %得到预测出来的数据
end
t1=1995:2004;
t2=1995:2014;
G, a, b % 输出预测值,发展系数和灰色作用量
plot(t1,A,'ko', 'LineWidth',2)
hold on
plot(t2,G,'k', 'LineWidth',2)
xlabel('年份', 'fontsize',12)
ylabel('污水量/亿吨','fontsize',12)
set(gca, 'LineWidth',2);
2.小波去噪
% 小波去噪
% 《MATLAB数学建模方法与实践》(《MATLAB在数学建模中的应用》升级版),北航出版社,卓金武、王鸿钧编著.
clc, clear all, close all,
load nelec.mat;
sig = nelec;
denPAR = {[1 94 5.9 ; 94 1110 19.5 ; 1110 2000 4.5]};
wname = 'sym4';
level = 5;
sorh = 's'; % type of thresholding
thr = 4.5;
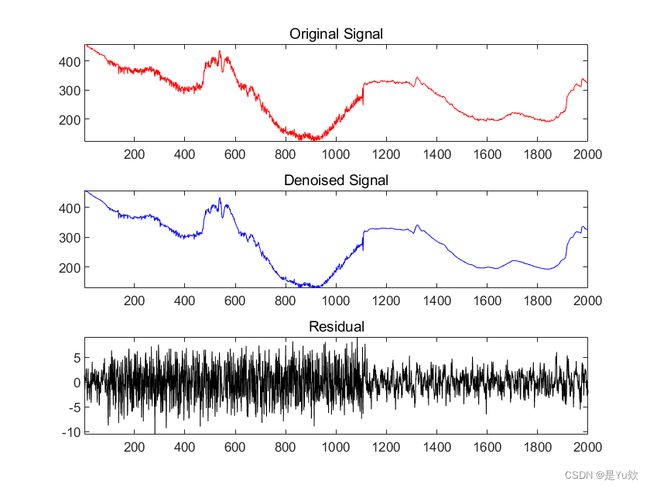
[sigden_1,~,~,perf0,perfl2] = wdencmp('gbl',sig,wname,level,thr,sorh,1);
res = sig-sigden_1;
subplot(3,1,1);plot(sig,'r'); axis tight
title('Original Signal')
subplot(3,1,2);plot(sigden_1,'b'); axis tight
title('Denoised Signal');
subplot(3,1,3);plot(res,'k'); axis tight
title('Residual');
% perf0,perfl2