物理概念在数据分析中的实践——阻尼
物理概念在数据分析中的实践——阻尼
作者: CPDA 数据分析师 刘程浩
最近我在编写一些课件,写着写着,有些过去已经看到几百次的,但是却没认真留意的概念引起了我的注意。因为有些算法模型对大多数人来说偏应用,你只要会用就行。但是如果要讲出来,让人听懂看懂,还真不是一回事儿。里面有很多概念,看似简单,想提一下然后就跳过去,但是到了后面再写的时候,发现之前跳过去的概念又见面了,还真绕不过去。于是我决定认真搞清楚这些概念的应用,也顺带做一个理解物理和数据分析之间的桥梁。
说到阻尼,物理学上的定义有很多种,力学和机械工程领域居多,电学也有,但我们就比较少接触。
我们最常看到的阻尼的例子,就是弹簧振动或者单摆运动,弹性振子或摆锤在周期性的运动中,因为受到“各种能量损失的影响”,从而其运动开始趋于稳态。要么振动周期越来越小直到停摆,要么稳定在一个比较小的振幅或频率上。这种“能量损失”中损失的能量到哪里去了,大部分是克服摩擦力去了。因此根据能量守恒,剩下用作维系原来运动的能量少了,原来的运动也就越来越趋稳了。
因此,如果学数据分析的时候,突然遇上一个方法论中有“阻尼”这个名词出来,估计一般人会觉得很莫名其妙。比方说Holt指数平滑和ETS中的趋势“阻尼系数”。
可能你高中学过物理,接触过刚才说的阻尼,但是书本上的例子还是单摆,
还是弹性振动,你可能还一下子联系不上这个物理概念和时间序列分析。他俩一个汪星人一个喵星人,咋就能结合在一起呢?
其实,物理学掌握“阻尼”的关键,在于“阻尼”对原来运动的影响,是使其原来的运动趋稳。而时间序列中的“阻尼”影响,也是关于某些“影响力”使得原来数据的趋势趋于稳定。
总之,两者之间联系的关键,就在于“改变原来的运动趋势”,使得原有的
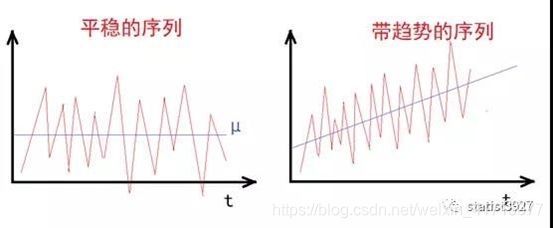
变化趋于稳定。单摆和弹性振动直观上很容易理解,不就是晃悠晃悠就停了吗,那时间序列的应用该如何理解呢?我们看下面2个对比图。如果一组数据,如果它是围绕着均值为μ上下随机变动,再加上一些额外的约束,例如方差恒定……那么我们认为它是平稳的。时间序列分析的起点,往往都是研究平稳时间序列。数据如果不平稳,也要想办法做各种变换,让它变得平稳。如果数据不是围绕一个均值上下随机变动,那么一般存在趋势或其他因素的影响。
对于这个变化的趋势,时间序列分析上有不同的处理,有的是把它消除掉,
例如做一次差分或两次差分。例如ARIMA中的I,是指单整的意思,单整的处理方法,主要就是差分。通过将带趋势的数据处理成平稳的状态,再套用研究平稳序列的方法来研究它。
有的则是保留它的趋势特点,并分离出来它的趋势特点,并加以研究。比方说holt指数平滑(也叫二次指数平滑),Holt-winters指数平滑(也叫三次指数平滑)中,还有它们的升级版 ETS模型,都会将这个趋势变化的状态方程给单列出来,研究趋势的逐步变化规律。
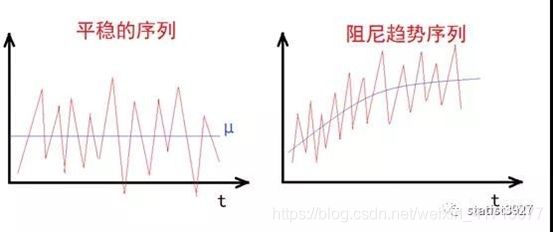
在上面第二种方法中,有种特殊的现象,即数据表现一开始是有趋势的,但是随着时间的推移,它的趋势慢慢变小了甚至消失了。为了搞清楚它的趋势消失的规律,也就在趋势的状态方程中添加了一个“衰减系数”,也叫做“阻尼系数”。
其实阻尼的英文单词damping,也就是有逐渐衰减的意思。
在这里不得不插入提一下东西方的研究特点差异。
已经不止几百位学者指出,东方的学问研究,讲究系统性和整体性。
例如中医,咳嗽不止时,中医会问你的痰啥颜色,末了可能给你开些清热的药,为啥?因为咳嗽是肺疾,肺属木,火克木而水生木。如果咳出来的痰液是黄绿色,那么说明肺上火了,上火就需要一些药性属阴或寒性的药物要来治疗。这就是站在一个中医五行的系统角度来看问题。
但西医则偏重于分析,基于解剖学将人体分成8大系统。你咳嗽了,那么就
专门针对呼吸系统一些指标是否正常进行检查,比方说听一下肺部支气管的呼吸,检查下痰液里某某杆菌的数量,或者再照一下X光,看看胶片上肺和支气管有没有感染的迹象……然后才给予开药治疗。绝不会让你去检查运动系统、消化系统啥的。
时间序列的分析刚好是西方人提出来的方法,正是很典型的符合了西方的
“分析法”。因为一个时间序列数据集中,包含了很多的信息,典型的分析法是将这些信息分成:趋势信息、季节信息、宏观周期信息、随机扰动信息,然后再对每种信息再进一步做细分,层层分解……例如趋势信息又分成线性趋势、非线性趋势、阻尼线性趋势、阻尼非线性趋势;这些趋势又和季节性因素有着加法影响和乘法影响……
也正是这种分析的思维,相当于对各种数据的“表象”进行了聚类,刚好有一类数据表象体现出了趋势的逐步衰减并趋于平稳的状态,那么就专门的提炼出了针对阻尼趋势的研究方法。
最早时间序列中用到阻尼的学者,有Flores,Pearce,在指数平滑分析中应用到阻尼这个概念的,应该当属Gardner。他在1985年的时候,就对holt指数平滑方法做了改进。他做了哪些改进呢,对就是加入了阻尼系数。让带线性趋势的指数平滑在对有逐渐衰减趋势的数据序列有了新的分析手段。
基于Gardner的研究基础,如果再加上季节性因素,非线性的趋势因素,那么指数平滑的分析方法应该是到了21世纪之后才变得更加完整。
下面我们就用一个稍微简单些的例子,来看下这个阻尼系数到底如何影响数据分析。我们就以包含了趋势和季节因素在内的holt-winters加法模型作为分析对象。
从上表左侧的holt-winters加法模型看出,(2)式子给出了一个时间序列
数据的趋势的变化演进过程,而相对应的带阻尼系数的holt-winters 加法模型 (6)式子则给出了阻尼趋势的演进过程。这2个过程其实在做回归或拟合的时候,两者的差异其实并不大的,因为它们都会动态的调整,通过β系数的取值不同而表现出来。
但是,在预测的时候,也就是(4)式和(8)式就会体现出比较明显的差异。原因很简单,因为在(4)中,未来趋势走向是一个线性方程 hbt,而(8)式中
的趋势走向虽然也是线性方程,但是它的斜率却小很多,明显的可以看出(8)式的预测值会明显比(4)式小。因此未来h期的预测总量也会有比较大的差异。但是这种差异我们是认可的,因为我们如果在研究拟合的过程中发现数据序列的趋势本身就是逐渐趋于平稳的,那么未来的这种惯性有更大的概率会保持下去,也就是说阻尼因素会持续影响到未来。这个是比较符合常见的业务实际的。我们就举个例子来看看,阻尼作用在时间序列上的应用。
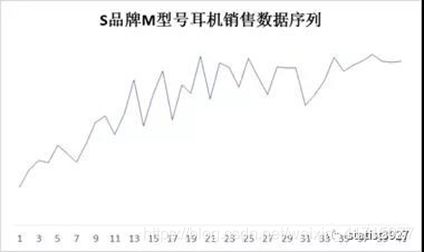
上图是S品牌M型号的耳机销售数据,光看到这个数据序列的时候,我们确实能看出数据有一个向上增长的趋势并且逐步趋稳,这有些像生命周期曲线中的
S型的前半段。
而且,像这种趋势逐渐变平稳的曲线也不少,例如用y=aln(x)+c或y=axb+c 函数图形也是这样的。
所以,一开始我们并不清楚到底用哪种模型来进行分析,于是我们索性都用
一次看看。
φ=0.9561,意味着阻尼或趋势衰减速度并不是很快,大约每期次衰减5%左右。
上表的4种模型里面,我们可以看到拟合效果 R2和残差正态检验都比较好。
尽管Holt-winters (带阻尼趋势)加法模型的 R2值稍微高一些,但是不得不
说,这种模型还是有其独特的优势,为了说明这些优势在业务上的体现,我们逐步分析
首先,我们看4种模型的拟合和预测效果图,图中我们可以看到,y=aln(x)+c 或 y=axb+c 函数预测时,预测区间表现出来的是2条平滑的曲线,实际在业务
应用时,或许这并不是我们想要的。因为从历史数据来看,每个其次的销量数据是有波动的,可能掺杂着季节因素。因此如果我们想了解各个预测期次的节奏的话,这显然做不到。
当然了,如果是想预测未来某段时间的总量的话,或许可用。因为考虑总量不用看节奏。
而Holt-winters加法模型以及带阻尼的加法模型,在预测区间内能刚好能克服上面曲线函数的这一点不足,也正是业务人员做预测时希望看到的参考。
- y=aln(x)+c 或 y=axb+c 函数做回归预测时,有个前提假设往往被忽
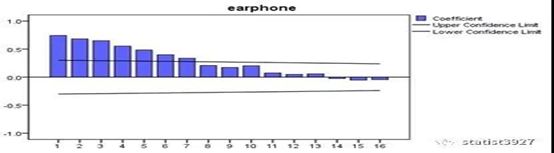
略,就是原数据不能自相关,换成截面数据的话来说,就是数据之间必须是独立同分布。但实际上我们通过ACF图观察一下发现自相关还是明显的,自相关函数呈拖尾,因此自回归的模型或许更能说明问题。因此做的回归效果及预测效果要打上一个问号。
而Holt-winters加法模型以及带阻尼的加法模型,本身就是要构建一个模型:这个模型中的数据被设定为有“记忆性”,比方说那些平滑系数就是最好的说明。因此有无自相关对它来说,有当然最好,没有也无妨。
- 最关键的一点,就是 y=aln(x)+c 或 y=axb+c 函数反应的是时间x和
销量y之间的关系,但是这个关系很难用业务语言进行解释。比方说,ln(x)在业务上表现是啥?你能说的清楚吗?
而Holt-winters 加法模型以及带阻尼的加法模型,能够将数据中的趋势、
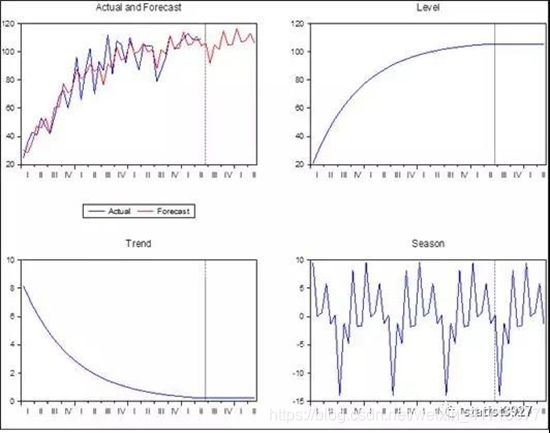
季节因素,乃至趋势变化的过程做分解说明,一目了然。比方说季节因素,有哪些波动规律,趋势变化从什么时候开始加速变缓等,让人能够对数据的变化规律有更多的认识。以下是以Holt-winters带阻尼的加法模型为例所带来的信息。
左一图的预测区间里,数据的趋势已经趋于平稳了,并且体现出了期次间的节奏。
左二图说明了趋势(纵坐标表示斜率)在第二年年中开始,趋势变得就比较平缓了,阻尼效果并不是很快就施加出来;第三年之后的期次可以认为趋势已经平稳了。这样一来或者说明了产品进入了稳定期,或者说增长利好的有利因素已经不明显了,或者说此时客户群体比较稳定了……等等。
右二图表示的季节性,可以看出每年Q2-Q3会比较淡,而Q1和Q4则为比较旺。并且每年的淡旺季的销量差异大约在30-40单位左右。
经过以上的对比,我们很容易就会发现,“阻尼”这个物理概念被数据分析引入后,更多的信息被挖掘出来,这样管理者做决策的时候的参考资料也就更多了。