【2022.12.14】备战春招Day9——每日一题 + 416. 分割等和子集 + 617. 合并二叉树
[每日一题] 1697. 检查边长度限制的路径是否存在
题目描述
给你一个 n 个点组成的无向图边集 edgeList ,其中 edgeList[i] = [ui, vi, disi] 表示点 ui 和点 vi 之间有一条长度为 disi 的边。请注意,两个点之间可能有 超过一条边 。
给你一个查询数组queries ,其中 queries[j] = [pj, qj, limitj] ,你的任务是对于每个查询 queries[j] ,判断是否存在从 pj 到 qj 的路径,且这条路径上的每一条边都 严格小于 limitj 。
请你返回一个 布尔数组 answer ,其中 answer.length == queries.length ,当 queries[j] 的查询结果为 true 时, answer 第 j 个值为 true ,否则为 false 。
输入:n = 3, edgeList = [[0,1,2],[1,2,4],[2,0,8],[1,0,16]], queries = [[0,1,2],[0,2,5]]
输出:[false,true]
解释:上图为给定的输入数据。注意到 0 和 1 之间有两条重边,分别为 2 和 16 。
对于第一个查询,0 和 1 之间没有小于 2 的边,所以我们返回 false 。
对于第二个查询,有一条路径(0 -> 1 -> 2)两条边都小于 5 ,所以这个查询我们返回 true 。
题目解析
【离线查询】:「离线」的意思是,对于一道题目会给出若干询问,而这些询问是全部提前给出的,也就是说,你不必按照询问的顺序依次对它们进行处理,而是可以按照某种顺序(例如全序、偏序(拓扑序)、树的 DFS 序等)**或者把所有询问看成一个整体(**例如整体二分、莫队算法等)进行处理。
与「离线」相对应的是「在线」思维,即所有的询问是依次给出的,在返回第 kk 个询问的答案之前,不会获得第 k+1k+1 个询问。
首先将 edgeList 按边长度从小到大进行排序,然后将queries 按 limit 从小到大进行排序,使用 k指向上一次查询中不满足limit 要求的长度最小的边,显然初始时 k=0。
【并查集】:添加链接描述
【查】:给定一个查询时,我们可以遍历edgeList中的所有边,依次将长度小于 imit 的边加入到并查集中,然后使用并查集查询 p 和 q是否属于同一个集合。如果 p 和 q属于同一个集合,则说明存在从 p到 q的路径,且这条路径上的每一条边的长度都严格小于 limit,查询返回true,否则查询返回 false。
【并】:如果 queries 的limit 是非递减的,显然上一次查询的并查集里的边都是满足当前查询的limit 要求的,我们只需要将剩余的长度小于limit 的边加入并查集中即可。
我们依次遍历 queries:如果 k 指向的边的长度小于对应查询的limit,则将该边加入并查集中,然后将 k 加 1,直到 k 指向的边不满足要求;最后根据并查集查询对应的 p 和 q是否属于同一集合来保存查询的结果。
class Solution {
public boolean[] distanceLimitedPathsExist(int n, int[][] edgeList, int[][] queries) {
//将edgeList按照边长从小到大的顺序排序
Arrays.sort(edgeList, (o1, o2) -> (o1[2] - o2[2]));
//将queries按照limit从小到大的顺序排序
Integer[] index = new Integer[queries.length];
for (int i = 0; i < queries.length; i++) {
index[i] = i;
}
Arrays.sort(index, (a, b) -> queries[a][2] - queries[b][2]);
// 构造并查集:节点
int[] uf = new int[n];
for(int i = 0; i < n; i++){
uf[i] = i;
}
boolean[] re = new boolean[queries.length];
int k = 0;//标识目前指向哪个边
for(int i : index){
while(k < edgeList.length && edgeList[k][2] < queries[i][2]){
//合并
merge(uf, edgeList[k][0], edgeList[k][1]);
k++;
}
//查
re[i] = find(uf, queries[i][0]) == find(uf, queries[i][1]);
}
return re;
}
public int find(int[] uf, int x){
if(uf[x] == x) return x;
return uf[x] = find(uf, uf[x]);
}
public void merge(int[] uf, int x, int y){
x = find(uf, x);
y = find(uf, y);
uf[y] = x;
}
}
【leetcode hot 100】
题目描述
给你两个单词 word1 和 word2, 请返回将 word1 转换成 word2 所使用的最少操作数 。
你可以对一个单词进行如下三种操作:
插入一个字符
删除一个字符
替换一个字符
题目解析
【动态规划】:该题是动态规划的经典题目。
-
dp数据的含义
dp[i][j]表示使得word1[0 - i] 和 word2[0 - j]相同,所做操作的最少次数。 -
初始化
dp[0][j] = j,表示当word1为空,word2不为空时,需要进行j次添加操作。
dp[i][0] = i,表示当word2为空,word1不为空时,需要进行i次添加操作。 -
状态转移方程
dp[i][j] = dp[i - 1][j - 1], 当word1[i] = word2[j]时
dp[i][j] = Math.min(dp[i][j - 1], dp[i - 1][j], dp[i - 1][j - 1])) + 1
class Solution {
public int minDistance(String word1, String word2) {
if(word1.length() == 0) return word2.length();
if(word2.length() == 0) return word1.length();
char[] array1 = word1.toCharArray();
char[] array2 = word2.toCharArray();
int[][] dp = new int[word1.length() + 1][word2.length() + 1];
//初始化
for(int i = 1; i <= word1.length(); i++){
dp[i][0] = i;
}
for(int i = 1; i <= word2.length(); i++){
dp[0][i] = i;
}
for(int i = 1; i <= word1.length(); i++){
for(int j = 1; j <= word2.length(); j++){
if(array1[i - 1] == array2[j - 1]){
dp[i][j] = dp[i - 1][j - 1];
}else{
dp[i][j] = Math.min(dp[i - 1][j - 1], Math.min(dp[i - 1][j], dp[i][j - 1])) + 1;
}
}
}
return dp[word1.length()][word2.length()];
}
}
【代码随想录】617. 合并二叉树
题目描述
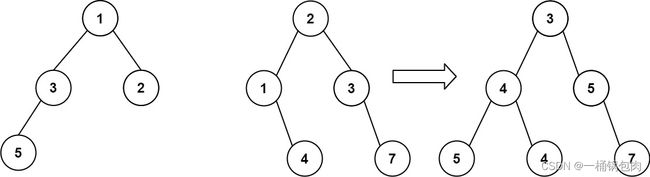
给你两棵二叉树: root1 和 root2 。
想象一下,当你将其中一棵覆盖到另一棵之上时,两棵树上的一些节点将会重叠(而另一些不会)。你需要将这两棵树合并成一棵新二叉树。合并的规则是:如果两个节点重叠,那么将这两个节点的值相加作为合并后节点的新值;否则,不为 null 的节点将直接作为新二叉树的节点。
返回合并后的二叉树。
题目解析
【递归】:使用树的先序遍历,将对应位置的节点相加。
class Solution {
public TreeNode mergeTrees(TreeNode root1, TreeNode root2) {
//递归
if(root1 == null) return root2;
if(root2 == null) return root1;
TreeNode new_head = new TreeNode(root1.val + root2.val);
new_head.left = mergeTrees(root1.left, root2.left);
new_head.right = mergeTrees(root1.right, root2.right);
return new_head;
}
}