opencv-python 学习笔记（9） ------模板匹配与霍夫变换

opencv-python 学习笔记（9） ------模板匹配与霍夫变换

9.1 模板匹配

9.1.1 原理

      所谓的模板匹配，就是在给定的图片中查找和模板最相似的区域，该算法的输入包括模板和图片，整个任务的思路就是按照滑窗的思路不断的移动模板图片，计算其与图像中对应区域的匹配度，最终将匹配度最高的区域选择为最终的结果。（有点类似双目立体匹配）。

9.1.2 实现流程

（1）准备两幅图像∶
原图像（L）∶ 在这幅图中，找到与模板相匹配的区域（最左）
模板（T）∶ 与原图像进行比对的图像块（中间）

（2）滑动模板图像和原图像进行比对∶

      将模板块每次移动一个像素（从左往右，从上往下），在每一个位置，都计算与模板图像的相似程度。·对于每一个位置将计算的相似结果保存在结果矩阵（R）中。如果输入图像的大小（WxH）且模板图像的大小（wxh），则输出矩阵R的大小为（W-w＋1，H-h＋1）。
（3）获得上述图像后，查找最大值所在的位置，那么该位置对应的区域就被认为是最匹配的。对应的区域就是以该点为顶点，长宽和模板图像一样大小的矩阵。

9.1.3 实现

代码：

cv2.matchTemplate(image,templ,method,[result,mask])

参数∶
imgage ：要进行模板匹配的图像·
templ ∶ 模板
method∶ 实现模板匹配的算法，主要有∶
      1.平方差匹配（CV_TM_SQDIFF）∶利用模板与图像之间的平方差进行匹配，最好的匹配是0，匹配越差，匹配的值越大。
      2.相关匹配（CV_TM_CCORR）∶利用模板与图像间的乘法进行匹配，数值越大表示匹配程度较高，越小表示匹配效果差。
      3.利用相关系数匹配（CV_TM_CCOEF）∶利用模板与图像间的相关系数匹配，1表示完美的匹配，-1表示最差的匹配。
      （注：完成匹配后，使用cv.minMaxLoc方法查找最大值所在的位置即可。如果使用平方差作为比较方法，则最小值位置就是最佳匹配位置。）
代码：

cv2.minMaxLoc()

参数：src：图像
返回值：最小值，最大值，最小值索引（2维），最大值索引（2维）
例子：

import cv2

target = cv2.imread("2.jpg")   # 图像
template = cv2.imread("2.0.jpg")  # 模板
theight, twidth = template.shape[:2]  # 模板的长、宽
result = cv2.matchTemplate( target , template, cv2.TM_SQDIFF_NORMED,-1)   # 模板匹配
min_val, max_val, min_loc, max_loc = cv2.minMaxLoc(result)  #最小值，最大值，最小值索引（2维），最大值索引（2维）
cv2.rectangle(target, min_loc, (min_loc[0] + twidth, min_loc[1] + theight), (0, 0, 225), 2)  #在原图上画长方形（左上右下）
cv2.imshow("aa", target)
cv2.imwrite('matchTemplate.jpg',target)
cv2.waitKey()
cv2.destroyAllWindows()

结果：

9.2 霍夫变换

用来提取图像中的几何形状，如图：

9.2.1 原理

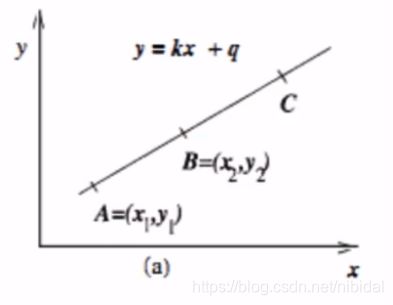
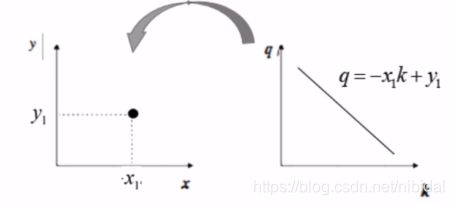
在直角坐标系中，一条直线由A=（x1，y1）和B=（x2，y2）确定，如下图所示：

将直线y=kx+q写成关于（k，q）的表达式：

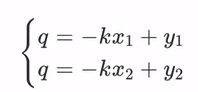
具体变换，如图：

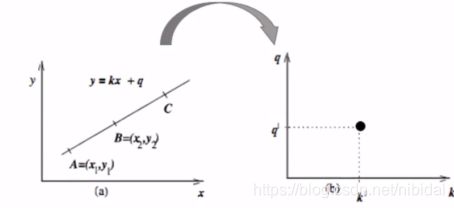
变换后的空间我们叫做霍夫空间。即笛卡尔坐标系中的一条直线，对应于霍夫空间中的一个点。反过来，则霍夫空间中的一条线，对应于笛卡尔坐标系中一个点如下：

而线段的A，B俩点对应情况如下：

（俩条直线相交）
三点共线的情况如下：

由此可知，如果在笛卡尔坐标系的点共线，那么这些点在霍夫空间中对应的直线交于一点。如果不止存在一条直线时，如下所示∶

A，B俩点，将其对应回直角坐标系中的直线：

注：特殊情况，如下图：

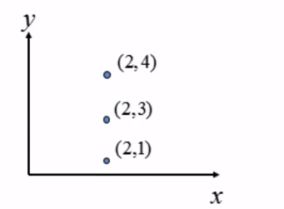
此时无法直接从直角坐标系转化为霍夫坐标系，所以需借助极坐标系。

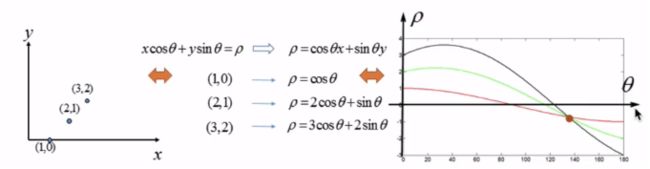
在极坐标下的情况是一样的，极坐标中的点对应于霍夫空间的线，这时的霍夫空间是不在是参数（k，g）的空间，而是（p，θ）的空间，p是原点到直线的垂直距离，θ表示直线的垂线与横轴顺时针方向的夹角，垂直线的角度为 0度，水平线的角度是180度。
我们只需求得霍夫空间的交点的位置，就可得到直角坐标系的直线。

9.2.2 实现流程

实现流程
      假设有一个大小为100*100的图片，使用霍夫变换检测图片中的直线，则步骤如下所示∶
（1）直线都可以使用（ρ，θ）表示，首先创建一个2D数组，我们叫做累加器，初始化所有值为0，行表示p，列表示θ。

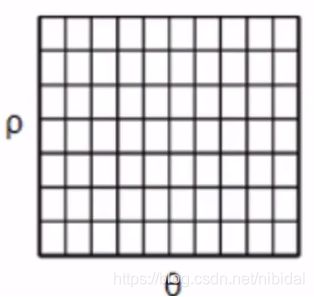
      该数组的大小决定了结果的准确性，若希望角度的精度为1度，那就需要180列。对于p，最大值为图片对角线的距离，如果希望精度达到像素级别，行数应该与图像的对角线的距离相等。
（2）取直线上的第一个点（z，y），将其带入直线在极坐标中的公式中，然后遍历θ的取值∶0，1，2，… 180，分别求出对应的p值，如果这个数值在上述累加器中存在相应的位置，则在该位置上加1.·取直线上的第二个点，重复上述步骤，更新累加器中的值。对图像中的直线上的每个点都直线以上步骤，每次更新累加器中的值。
（3） 搜索累加器中的最大值，并找到其对应的（p，θ），就可将图像中的直线表示出来。

9.2.3 实现

代码：

cv2.HoughLines(image,rho,theta,threshold,[lines,srn,stn,min_theta,max_theta])

参数：
Image：图像（二值化的图像）；
rho，theta：ρ、θ的精确度；
threshold：阈值，只有累加器的值高于它才是直线。