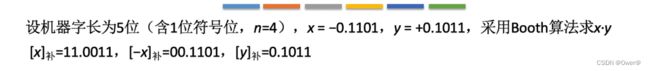运算方法和运算器
目录
定点加减运算
补码加法运算
例
补码减法运算
例
溢出概念及检测方法
溢出的检测方法及解决办法
(1)采用双进位的进位判别
(2)采用双符号为的方法
解决方法:
例
定点乘法运算
移位与舍入操作
原码一位乘法
例
补码一位乘法
例
浮点运算
浮点加减运算
定点加减运算
在计算机中进行加减运算,便于运算,都采用补码的形式,在运算的过程中不需要比较两数的大小和正负。
补码加法运算
[x+y]补=[x]补+[y]补,在计算机中进行加法运算。
需要进行的过程为:
真值数---->原码----->补码----->补码相加结果----->原码------->真值数
注意:
1、符号位与数值位便于区分加逗号,且符号位参与运算中。
例
x= -1101,y=+0110, 利用加法运算求 x + y
补码减法运算
计算机中便于进行减法运算,将减法运算转换为加法运算,也就是将减数进行变号处理。
x - y = [x]补 + [ -y ]补码= [x]补 + [ [y]补 ]变补,([ [y]补 ]变补 = [-y]补)。
变补是在补码的基础上,不论正负,包括符号位按位取反,然后加一。
补码减法运算进行的过程为:
真值数----->原码------>补码------->减数进行变补------>补码与补码的变补相加------>原码----->真值数
例
x= -1001,y=+0101, 利用减法运算求 x - y
溢出概念及检测方法
溢出:运算的过程中,如果超出机器字长所能表示的数据范围称为溢出。
如果超出机器所能表示的最大正数,称为正溢出,反之负溢出。
溢出的检测方法及解决办法
(1)采用双进位的进位判别
一句话概括:如果在运算的过程中,数值位的最高位的进位与符号位的进位相同,则没有溢出,否则溢出。
此方法仅仅方便判断运算是否溢出,并无解决方法。
(2)采用双符号为的方法
采用将补码的符号位扩充为两位,并且参与运算。双符号位的补码也称为变形补码。
1、如果双符号位相同:
双符号位为00,结果为正数;双符号位为11,结果为负数。
2、如果双符号位相异则溢出:
双符号位为10,结果为负溢出;双符号位为01,结果正溢出。
解决方法:
运算结束后,根据双符号位判断是否溢出。溢出的,双符号位的低位作为数值位的最高位,(换言之,整体右移,区别符号位和数值位的逗号左移一位)。
例
定点乘法运算
移位与舍入操作
在进行乘法运算前,需要了解移位的操作。二进制自身可以进行乘除运算,二进制左移相当于乘以2,右移相当于除以2。
对于左移右移,原有的二进制数移位后如何进行补位操作,需要分情况:
无论正负数,在移位的操作过程中,符号位都保持不变。
1、原码的移位:无论正负数,符号位不变,移位后空出的位补0。
2、补码的移位:对于正数,符号位不变,无论左移还是右移,空出的位补0;
对于负数,符号位不变,左移时,低位补0;右移时,高位补1;
移位操作可能出现的误差问题:
如果右移前,低位为1,右移后会出现误差;左移后,如果超出机器字长表示的范围,会溢出,出现误差。
舍入操作
移位后,如果超出机器字长的位数,需要进行舍入操作。
原码一位乘法
二进制的乘法操作与十进制的类似,乘数从低位依次开始与被乘数相乘,每次结果相乘后错位,最后将结果相加。但在计算机中,并不是最后把每次相乘的结果相加。
原码一位乘法,对于n位数相乘,需进行 n 次加法和 n 次移位。
对于原码,符号位不进行运算,两乘数的符号位采用逻辑的操作判断正负,只对数值位进行乘法运算。
在乘法过程中需要了解的名词,乘数的每一位与被乘数相乘的称为“位积”,每一次位积的累加结果称为“部分积”。
其中在每一次的加法运算中,存放位积的寄存器和被乘数的寄存器中的内容作为一个整体右移,被乘数的低位舍去,次低位移到低位参与下一次的乘法运算,而被乘数的最高位由位积的低位补上,位积的最高位补0。
只要被乘数的低位为1,位积需要加上被乘数,低位为0,位积加上0,不变。
例
补码一位乘法
采用直接补码乘法(Booth算法)
补码的符号位参与运算。采用变形补码的方式进行操作。补码与原码不同的时,在操作的过程中会出现加减操作。位积和被乘数采用双符号位补码的形式,乘数采用单符号位补码的形式。
补码的一位乘法需要进行 n 次累加,n - 1次移位,最后一次不用移位。
乘法的过程与原码类似,进行移位和累加操作。不同的是,每一次部分积和位积需要判断进行加减法操作。根据被乘数的最后两位数进行判断,如果为01,部分积加上位积;10,部分积减去位积;如果两数相同,部分积加0,不变。注意:补码的移位操作,补码的部分积累加或累加进行移位操作时,双符号位不变,移位后空出的高位补与符号位相同的数。
例
浮点运算
浮点加减运算
浮点数的格式包括阶码和尾数两部分。
浮点加减运算的步骤为:对阶、尾数加减运算、规格化处理、舍入操作、溢出判断。
步骤一:对阶
对阶的作用,在计算机中,两浮点数阶码相同,尾数加减运算时更方便。
两浮点数的阶差判断,△E=Ex-Ey
阶码判断时都采用变形补码的形式,若△E=0,阶码相同,进行下一步骤;若△E > 0,后者的阶码小,(需要对阶处理,为减小对阶过程中的误差,采用小阶码向大阶码对齐),尾数每右移一位,阶码加1,直到阶码相等为止; 若△E < 0,前者同样采取对阶处理。
步骤二:尾数加减运算
对阶完成后,尾数采用变形补码的形式进行同定点的加减运算。
步骤三:规格化处理
尾数加减后的结果进行规格化处理。若结果为非规格化,根据结果情况左移右移至规格化,每一次移位阶码也进行加减。
步骤四:舍入操作
因位数有限,尾数移位后造成的问题。常采用舍0入1(类似四舍五入,超出的位若为1,入1也就是尾数低位加1,可能会造成溢出的问题需要再次右规再次同样的操作,超出位为0,舍去)、直接置1的方法。
步骤五:溢出判断
溢出判断是根据阶码的变形补码的形式的双符号位进行判断,(浮点数的阶码决定范围,尾数的位数决定精度)。