二叉树——表达式转换
论如何把后缀表达式转成前缀表达式
首先,我们开门见山!——
先从表达式树开始说起:
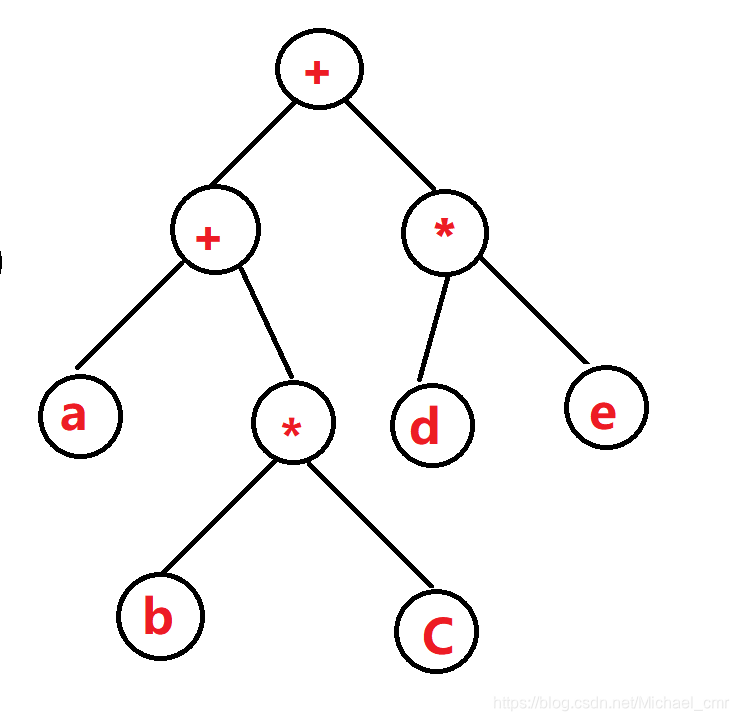
这就是一个典型的表达式树,假设我们表达式树的叶节点是操作数(简单理解成数字),表达式树的叶节点是操作数(简单理解为+ - * / 这些字符),假设所有的运算符都是双目运算符,那么刚好形成一棵二叉树,然后我们就可以非常非常easy的遍历这课树来获得——前缀、中缀、后缀表达式,
它们的关系分别为——
前序遍历:前缀表达式
中序遍历:中缀表达式
后序遍历:后缀表达式
假设我们现在有了一棵非常非常厉害的 表达式树
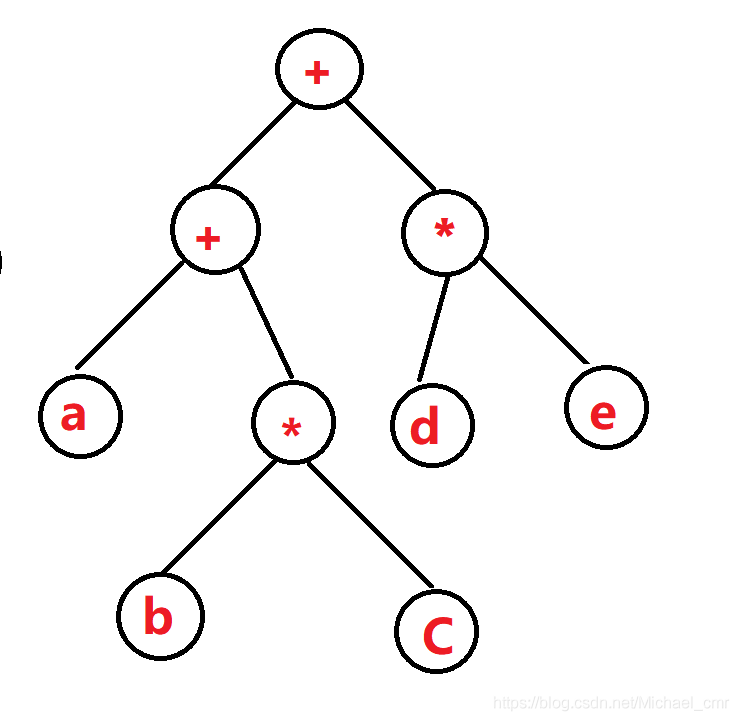
它的前序遍历:++abcde——这就是前缀表达式
中序遍历:a+bc+de——这就是中缀表达式(我们最熟悉的)
后序遍历:abc*+de*+——这就是后缀表达式
当然,现在我们面临的一个问题,就是如何将后缀表达式转化成一棵无敌的二叉树!
后缀表达式建树
1.大致思路
举例说明!
假设我们有后缀表达式 12+34++ ,就是我们常见的1+2+3+4转换成后缀的样子
first,我们先有一个栈
(状态初始化为空)
然后——我们从左往右扫这个后缀表达式12+34++
接着,我们扫到了 2 ,还是数字,进栈
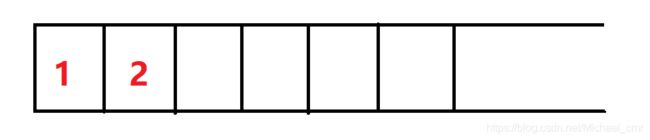
现在栈的状态——1 2
继续扫描,扫到了操作符 +,弹出栈顶的两个元素,与加号建成一棵二叉树,然后将这课二叉树入栈
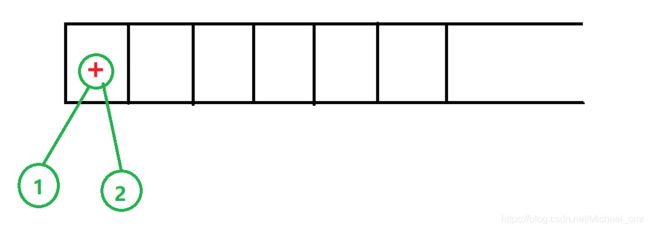
就长这个丑样子
再扫描表达式,数字3,进栈。
然后数字4,进栈
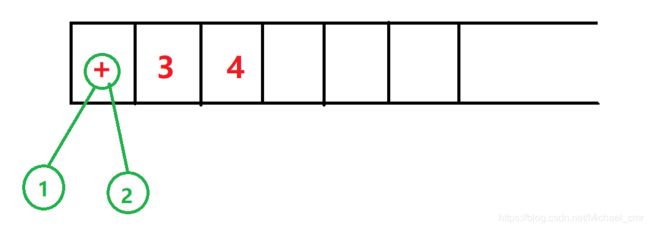
现在栈的状态就是上面这个样子
扫完3和4,接下来就是两个加号 +
栈的状态分别为
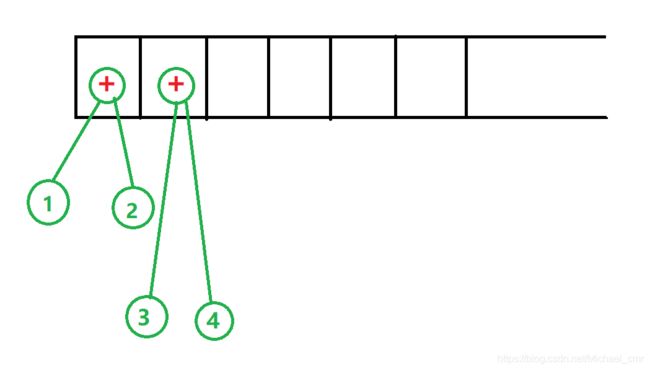
然后是——
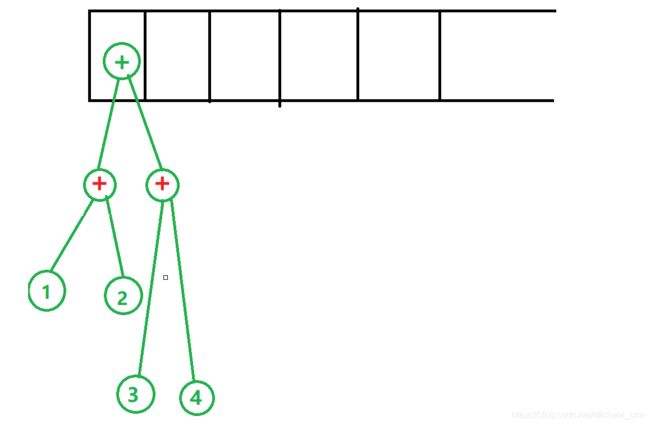
于是,由图可得,我们栈顶的那个元素就是那个我们需要的二叉树(表达式树)。但是,现在我们, 面临着一个非常严肃的问题——如何用代码实现!
代码实现
我们先分布介绍,最后在总结在一起!
1.结构体部分(栈的结构、二叉树的结构)
首先——二叉树必备部分是数据域、指针域(左孩子、右孩子、父亲节点)
//创造二叉树的节点构造
typedef struct node
{
char data; //数据域
node *lc; //左
node *rc; //右
}*TREE;
接着,二叉树的结构
typedef struct node_father
{
TREE father;
}Tree;
解决了二叉树的结构,我们来构造栈的结构
//栈的节点构造
typedef struct Stack
{
Tree tree; //存储数根(数据域)
Stack *next; //指向下一个节点
}*Stack_;
接着,栈的构造——
typedef struct stack_
{
Stack_ top; //指向栈顶元素
int l; //栈的长度
}stack;
构造完基本的结构后,我们还要加入一个枚举类型的变量(其实不用也可以),但是为了代码的通俗易懂(可读性强,我们加入一个)
//枚举是左孩子还是右孩子
typedef enum is_child
{
_left=1,
_right=2
}is_child;
结束了基本的结构后,我们开始写它们的function,它们的功能以及基本操作
2.函数部分
首先,先来写关于建树的函数——
//创建树节点 (左右均为空)
TREE buildroot(char c)
{
TREE value=(TREE)malloc(sizeof(node)); //这句话尤其重要,分配内存是是否段错误的根本
value->data=c;
value->lc=value->rc=NULL;
return value;
}
然后,就是一个插入根节点的函数——
//插入根节点
void insert_root(Tree *tree,TREE value)
{
tree->father=value;
}
接着,我们来做合并二叉树的函数——
//合并二叉树
void merge(Tree *father,Tree *child,is_child flag)
{
if(flag==_left)
father->father->lc=child->father;
else
father->father->rc=child->father;
}
上面都是二叉树的操作,然后我们要写栈的操作:
先来初始化栈——
void initstack(stack *sta) //初始化栈
{
sta->l=0;
sta->top=NULL;
}
然后是入栈操作——
void push(stack *sta,Tree t)
{
Stack_ value=(Stack_)malloc(sizeof(Stack));
value->tree=t;
value->next=sta->top;
sta->top=value;
sta->l++;
}
接着出栈——
void pop(stack *sta,Tree *t)
{
if(sta->top==NULL) //这是为了防止空栈时我们pop后会爆栈(STL栈在空栈的时候执行pop操作就会爆栈)
return;
Stack_ value=sta->top;
(*t)=value->tree; //这里就把我们栈顶的值赋给了传进来的Tree
sta->top=value->next;
sta->l--;
}
我们也可以再多此一举的写一个结构体来封装栈的功能
typedef class function_sta
{
public:
void initstack(stack *sta) //初始化栈
{
sta->l=0;
sta->top=NULL;
}
void push(stack *sta,Tree t)
{
Stack_ value=(Stack_)malloc(sizeof(Stack));
value->tree=t;
value->next=sta->top;
sta->top=value;
sta->l++;
}
void pop(stack *sta,Tree *t)
{
if(sta->top==NULL)
return;
Stack_ value=sta->top;
(*t)=value->tree;
sta->top=value->next;
sta->l--;
}
}fun_s;
因为我们C++是面向对象的语言,感觉要是不用class(类)来写的话,就太偏向C语言了。(不能太偏心)
写完后,我们迎来了最重要的一个部分——生成表达式树的部分
3.生成表达式树
//构造表达式树
void build_poland(Tree *tree)
{
stack s;
fun_s sta;
sta.initstack(&s);
for(int i=0;i<l_1;i++)
{
TREE val=buildroot(ch[i]); //得到一个父节点为ch[i],两个子节点为空的二叉树
Tree left,right,father;
if(cmp(ch[i])) //如果是运算符 ,那么将栈顶的两个元素弹出,与运算符建立成二叉树,然后再把生成的二叉树入栈
{
insert_root(&father,val); //插入节点(建立一个二叉树)
sta.pop(&s,&right); //出栈
merge(&father,&right,_right); //合并到右孩子去
sta.pop(&s,&left); //出栈
merge(&father,&left,_left); //合并到左孩子去
sta.push(&s,father); //入栈
}
else //如果不是运算符 ,那么直接入栈
{
insert_root(&father,val); //插入节点(建立一个二叉树)
sta.push(&s,father);
}
}
sta.pop(&s,tree); //这是结果的值
}
当然,我们会发现,上面有一个cmp函数还没定义
#define cmp(c) (c=='+'||c=='-'||c=='*'||c=='/')
这就是cmp函数的定义,意思是判断这个字符只不是运算符,如果是——返回1(true);
不是——返回0(false)
这个build_poland函数里面还有一个ch[], 和 l_1,没有讲到;
其实,ch[] ,就是我们存表达式的字符串, 而 l_1 就是这个字符串的长度。
我们在全局区定义——
char ch[50005]; //表达式
int l_1; //长度
但是,为了通用性,我们也可以在build_poland函数里面这么写
void build_poland(Tree *tree,char ch[])
{
stack s;
fun_s sta;
sta.initstack(&s);
int l_1=strlen(ch);
for(int i=0;i<l_1;i++)
{
TREE val=buildroot(ch[i]); //得到一个父节点为ch[i],两个子节点为空的二叉树
Tree left,right,father;
if(cmp(ch[i]))
{
insert_root(&father,val); //插入节点(建立一个二叉树)
sta.pop(&s,&right); //出栈
merge(&father,&right,_right); //合并到右孩子去
sta.pop(&s,&left); //出栈
merge(&father,&left,_left); //合并到左孩子去
sta.push(&s,father); //入栈
}
else //如果不是运算符 ,那么直接入栈
{
insert_root(&father,val); //插入节点(建立一个二叉树)
sta.push(&s,father);
}
}
sta.pop(&s,tree);
}
这样我们就有了这个函数的通用性
最后,我们要写树的三种遍历方式,来遍历表达式树,得到三种表达式
//先序遍历输出结果;
void first(TREE tree)
{
if(tree==NULL)
return;
putchar(tree->data);
first(tree->lc);
first(tree->rc);
}
//中序遍历输出结果;
void second(TREE tree)
{
if(tree==NULL)
return;
second(tree->lc);
putchar(tree->data);
second(tree->rc);
}
//后序遍历输出结果;
void last(TREE tree)
{
if(tree==NULL)
return;
last(tree->lc);
last(tree->rc);
putchar(tree->data);
}
最后是我们的终极的目标——main函数
int main()
{
gets(ch); //输入后缀表达式
l_1=strlen(ch); //得到表达式长度
Tree ans; //表达式树
build_poland(&ans); //得到表达式树
first(ans.father); //输出前缀表达式
puts(""); //遍历完成,输出换行
second(ans.father); //输出中缀表达式
puts(""); //遍历完成,输出换行
last(ans.father); //输出后缀表达式
puts(""); //遍历完成,输出换行
return 0;
}
大致我们的表达式转换就完成了!
运行结果:
输入——12+34++
输出——
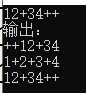
是正确的!程序没毛病~
完整代码展示——
#include好了,讲到这里,完结了。
若是对这些有兴趣的,请一定一定关注我,一起多多学习
我是Michael_cmr,蒟蒻一枚。如果有说错的地方,各位大神千千万万要指出来。
谢谢大家!欢迎各位大神指点!
(转载请标注出处与楼主姓名)
(QQ:2437844684)
(欢迎各位大神评论)
——————都看到这里了,不点个赞是不是也觉得不好意思呀~