3D目标检测实战 | 详解2D/3D检测框交并比IoU计算(附Python实现)

1 交并比基本概念

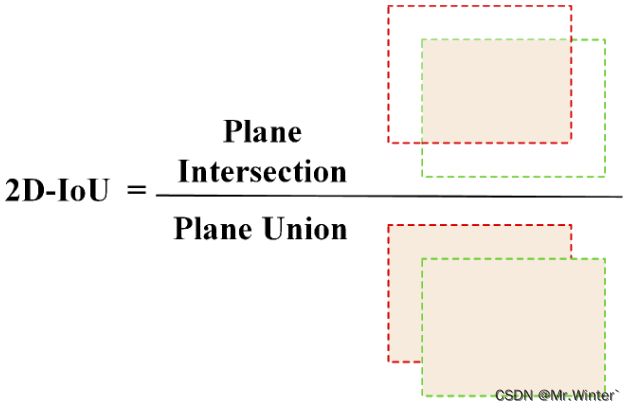
交并比(Intersection Over Union, IoU)是度量两个目标检测框交叠程度的方式，公式如下

$$\mathrm{IoU}=\frac{\mathrm{area}({\mathrm{B}}_{\mathrm{p}}\cap {\mathrm{B}}_{\mathrm{gt}})}{\mathrm{area}({\mathrm{B}}_{\mathrm{p}}\cup {\mathrm{B}}_{\mathrm{gt}})}$$

其中${\mathrm{B}}_{\mathrm{gt}}$代表真值(Ground Truth)，${\mathrm{B}}_{\mathrm{p}}$代表预测值

$\mathrm{IoU}$是一种常用的评估目标检测算法性能的指标，其计算的意义如下：

• 确定目标的匹配程度：通过比较检测框和真实标注框的重叠部分与总体部分的比例，可以确定目标检测算法对于不同尺寸、形状和姿态的目标的匹配程度。较高的$\mathrm{IoU}$值表示检测框与真实标注框更好地匹配
• 设定阈值进行筛选：$\mathrm{IoU}$可以用于设定阈值来筛选检测结果。设定一个特定的$\mathrm{IoU}$阈值，只有当目标检测框与真实标注框的$\mathrm{IoU}$超过该阈值时，才认为检测结果是有效的。这有助于控制误检率和漏检率，提高目标检测的精确性和稳定性
• 评估算法性能：通过统计一系列目标检测结果的$\mathrm{IoU}$值，可以计算出平均$\mathrm{IoU}$或者其他评估指标，用于评估目标检测算法的整体性能。这有助于比较不同算法的准确性、鲁棒性和适应性

综上所述，$\mathrm{IoU}$是评估和改进目标检测算法的关键工具之一，下面介绍具体如何计算

2 2D检测框IoU计算

2D检测框的$\mathrm{IoU}$计算比较直接，就是按照公式

$$\mathrm{IoU}=\frac{\mathrm{area}({\mathrm{B}}_{\mathrm{p}}\cap {\mathrm{B}}_{\mathrm{gt}})}{\mathrm{area}({\mathrm{B}}_{\mathrm{p}}\cup {\mathrm{B}}_{\mathrm{gt}})}$$

计算面积，具体如下所示

def cal2dBoxOverlap(g_boxes, q_boxes, criterion=-1):
    N, K = g_boxes.shape[0], q_boxes.shape[0]
    overlaps = np.zeros((N, K), dtype=g_boxes.dtype)
    for k in range(K):
        qbox_area = ((q_boxes[k, 2] - q_boxes[k, 0]) * (q_boxes[k, 3] - q_boxes[k, 1]))
        for n in range(N):
            gbox_area = (g_boxes[n, 2] - g_boxes[n, 0]) * (g_boxes[n, 3] - g_boxes[n, 1])
            iw = (min(g_boxes[n, 2], q_boxes[k, 2]) - max(g_boxes[n, 0], q_boxes[k, 0]))
            if iw > 0:
                ih = (min(g_boxes[n, 3], q_boxes[k, 3]) - max(g_boxes[n, 1], q_boxes[k, 1]))
                if ih > 0:
                    ua = (gbox_area + qbox_area - iw * ih)      
                    overlaps[n, k] = iw * ih / ua
    return overlaps

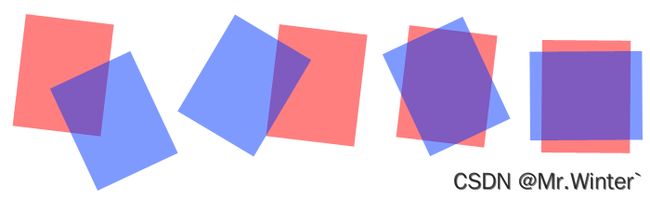
3 旋转2D检测框IoU计算

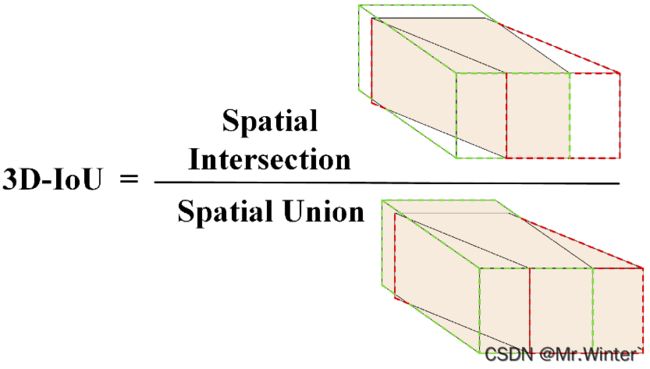
与2D目标检测不同，3D目标检测需要使用3D立方体来表示目标物体的位置和姿态。计算IoU时，需要考虑立方体的3D空间位置、大小和朝向的匹配程度

通常的算法步骤是：

• 压缩高度信息，计算平面内两个旋转2D检测框的重叠面积

• 在高度维度计算重叠高度
• 重叠面积乘以重叠高度计算重叠体积，从而计算IoU

本节介绍旋转2D检测框重叠面积的计算

def inter(rbbox1, rbbox2):
    corners1 = cuda.local.array((8, ), dtype=numba.float32)
    corners2 = cuda.local.array((8, ), dtype=numba.float32)
    intersection_corners = cuda.local.array((16, ), dtype=numba.float32)

    rbbox2corners(corners1, rbbox1)
    rbbox2corners(corners2, rbbox2)

    num_intersection = quadrilateralIntersection(corners1, corners2, intersection_corners)

    sortVertexInConvex(intersection_corners, num_intersection)

    return area(intersection_corners, num_intersection)

其中quadrilateralIntersection()函数计算了重叠部分的顶点信息，具体而言，通过求直线的交点和判断顶点是否在四边形内部来确定

def quadrilateralIntersection(pts1, pts2, int_pts):
    num_of_inter = 0
    for i in range(4):
        if pointInQuadrilateral(pts1[2 * i], pts1[2 * i + 1], pts2):
            int_pts[num_of_inter * 2] = pts1[2 * i]
            int_pts[num_of_inter * 2 + 1] = pts1[2 * i + 1]
            num_of_inter += 1
        if pointInQuadrilateral(pts2[2 * i], pts2[2 * i + 1], pts1):
            int_pts[num_of_inter * 2] = pts2[2 * i]
            int_pts[num_of_inter * 2 + 1] = pts2[2 * i + 1]
            num_of_inter += 1
    temp_pts = cuda.local.array((2, ), dtype=numba.float32)
    for i in range(4):
        for j in range(4):
            has_pts = lineSegmentIntersection(pts1, pts2, i, j, temp_pts)
            if has_pts:
                int_pts[num_of_inter * 2] = temp_pts[0]
                int_pts[num_of_inter * 2 + 1] = temp_pts[1]
                num_of_inter += 1

    return num_of_inter

得到重叠多边形后，通过切割三角形来计算面积

def area(int_pts, num_of_inter):
    area_val = 0.0
    for i in range(num_of_inter - 2):
        area_val += abs(trangleArea(int_pts[:2], int_pts[2 * i + 2:2 * i + 4],
                        int_pts[2 * i + 4:2 * i + 6]))
    return area_val

4 3D检测框IoU计算

加上高度维度的重叠信息即可计算3D检测框IoU，这部分与2D检测框IoU计算类似，不再赘述

def cal3dBoxOverlap(g_boxes, q_boxes, r_inc, criterion=-1):
    N, K = g_boxes.shape[0], q_boxes.shape[0]
    overlaps = np.zeros((N, K), dtype=g_boxes.dtype)
    for n in range(N):
        for k in range(K):
            if r_inc[n, k] > 0:
                iw = (min(g_boxes[n, 1], q_boxes[k, 1]) - max(
                    g_boxes[n, 1] - g_boxes[n, 4], q_boxes[k, 1] - q_boxes[k, 4]))
                if iw > 0:
                    area1 = g_boxes[n, 3] * g_boxes[n, 4] * g_boxes[n, 5]
                    area2 = q_boxes[k, 3] * q_boxes[k, 4] * q_boxes[k, 5]
                    inc = iw * r_inc[n, k]
                    ua = (area1 + area2 - inc)
                    overlaps[n, k] = inc / ua
    return overlaps

本文完整工程代码请通过下方名片联系博主获取

---

更多精彩专栏：

• 《ROS从入门到精通》
• 《Pytorch深度学习实战》
• 《机器学习强基计划》
• 《运动规划实战精讲》
• …

源码获取 · 技术交流 · 抱团学习 · 咨询分享 请联系