二叉树递归

111. 二叉树的最小深度（e）

总结：是求最小深度，相当于求最短路径，因此bfs优于dfs，思路2最优。

思路1：  递归深搜（求最值、递归函数需要返回值）

(1) 递归类型：从下到上

(2) 递推关系：对一个cur 其dep = 1 + min(leftdep, rightdep);

(3) 基本情况(收敛条件)：对一个nullptr， if has neighber, return INT_MAX; else return 根据题意0 or 1;

    // (1) 对一个cur 其dep = min(leftdep, rightdep);
    // (2) 对一个nullptr， if has neighber, return INT_MAX; else return 根据题意0 or 1;
    // (3) 递归类型：从下到上
    int minDepth(TreeNode* root) {
        int res = minDepth(root, 0);
        return res;
    }
    int minDepth(TreeNode* cur, int hasBrother)
    {
        if (cur == nullptr) {
            return hasBrother == 1 ? INT_MAX : 0;
        }
        int leftDep = minDepth(cur->left, cur->right != nullptr ? 1 : 0);
        int rightDep = minDepth(cur->right, cur->left != nullptr ? 1 : 0);
        return 1 + min(leftDep, rightDep);
    }

思路2：bfs迭代， 层序遍历. 

解法1 收敛时直接退出--更优

收敛条件: 第一个叶节点时return。

    int minDepth2(TreeNode* root) {
        queue qe;
        if(root == nullptr) {
            return 0;
        }
        int depth = 0;
        qe.push(root);
        while(!qe.empty()) {
            int curSize = qe.size();
            for(int i=0; ileft == nullptr && node->right == nullptr) { // 收敛条件
                    return ++depth;  //不能写depth++;
                }
                if(node->left) {
                    qe.push(node->left);
                }
                if(node->right) {
                    qe.push(node->right);
                }
            }
            depth++;
        }
        return depth;
    }

思路2：bfs迭代， 层序遍历.

解法2： 可以剪枝--没有解法1好，解法2多次一举

收敛条件: 第一个叶节点时return。

剪枝：若当前节点的深度小于当前整棵树的深度，则剪掉该分支

    int minDepth1(TreeNode* root)
    {
        if (root == NULL) {
            return 0;
        }
        queue> q;
        int res = INT_MAX;
        q.push({root, 1});
        while (!q.empty()) {
            int size = q.size();
            for (int i = 0; i < size; i++) {
                auto t = q.front();
                q.pop();
                auto cur = t.first;
                auto dep = t.second;
                if (cur->left == nullptr && cur->right == nullptr) { // 收敛条件
                    res = min(res, dep);
                    return res;
                }
                if (cur->left != nullptr && res > dep) { // 剪枝
                    q.push({cur->left, dep + 1});
                }
                if (cur->right != nullptr && res > dep) { // 剪枝
                    q.push({cur->right, dep + 1});
                }
            }
        }
        return res;
    }

104. 二叉树的最大深度(m)

总结：是求最大深度，只能遍历完整颗树才能知道结果，所以用dfs和bfs都一样。

思路1：递归（求最值、递归函数需要返回值）

//  递归类型：从下到上

// 递推关系：1 + max(leftdep, rightdep);

// 基本情况(终止条件)：遍历到叶节点的left和right.

    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }

思路2：bfs通用模板，层序遍历

    int maxDepth(TreeNode* root) {
        if (root == nullptr) {
            return 0;
        }
        queue q;
        q.push(root);
        int ans = 0;
        while (!q.empty()) {
            int sz = q.size();
            while (sz > 0) {
                TreeNode* node = q.front();
                q.pop();
                if (node->left) {
                    q.push(node->left);
                }
                if (node->right) {
                     q.push(node->right);
                }
                sz -= 1;
            }
            ans += 1;
        } 
        return ans;
    }

112. 路径总和(e)

 思路：

回溯(求是否有解，递归函数返回bool)：找到一个可行解就可以return，不须记录路径本身

基本情况(终止条件, 遍历到最后节点)：叶节点的left和right

收敛条件(找到可行解)：叶节点时递归后的sum == 叶节点的val

没法剪枝：必须要遍历到叶节点才能知道是否收敛，各节点的val没说是正整数，可正可负。

    bool hasPathSum(TreeNode* root, int sum) {
        if (root == nullptr) {
            return false;
        }
        if (root->left == nullptr && root->right == nullptr) {
            return sum == root->val ? true : false;
        }

        return hasPathSum(root->left, sum - root->val) ||
            hasPathSum(root->right, sum - root->val);
    }

113. 路径总和 II --二叉树的回溯比较特殊，遍历候选集与候选集节点的val加入path不在一个时空。因此会改变恢复现场的位置（见https://blog.csdn.net/u011764940/article/details/105592965，重点1、重点12）。

    思路：回溯（求所有可行解）:求所有可行解，需遍历整颗树

    // 基本情况(终止条件, 遍历到最后节点)：叶节点的left和right

    // 收敛条件(找到可行解)：cur叶节点时 叶节点的val == sum.

    // 没法剪枝：因为cur->val可正可负，必须要遍历整颗树才能找到所有路径。

    // 注：

    // (1)在回溯函数内部，path选了cur，就一定要走到撤销cur，path选和撤销中间不能有return，否则path不对应。(回溯基本结构) 。见回溯重点1：回溯算法解子集、组合、排序_u011764940的博客-CSDN博客

    // 换个角度看：角度1：本轮的候选集cur->left和cur->right的值val需要延时到递归下一轮处加入路径path。角度2：正着看就是加入路径path的cur是早于本轮候选集cur->left和cur->right的，因此恢复现场cur也需要在递归完孩子节点cur->left和cur->right后进行恢复。

// (2)因为收敛时直接把path加入结果集，所以一定要在收敛判断之前把cur加入path，而只有这样才能保证用例集只有一个节点且收敛的用例

    // (3)因为是把cur作为候选点加入path，那么cur的left和right就不再是在本轮待加入paht的候选集，只是做为递归到下一轮去做那个cur候选点。

    // (4)cur的left、right子树遍历完了，才会撤销path中的cur

    vector> pathSum(TreeNode* root, int sum) {
        vector> res;
        if (root == nullptr) {
            return res;
        }
        vector path;
        Backtrack(root, sum, path, res);
        return res;
    }

    void Backtrack(TreeNode* cur, int sum, vector &path, vector> &res)
    {
        if (cur == nullptr) {
            return;
        }
        path.push_back(cur->val); // 选cur(cur本身作为候选点，选入path)
        if (cur->left == nullptr && cur->right == nullptr) { // 叶
            if (sum == cur->val) { // 选cur后根据cur的值判断是否收敛
                res.push_back(path);
            }
            // 这里一定不能return, 因为在收敛条件之前选了cur， 一定让代码走到撤销cur的地方。
        }
        // cur的left和right在本轮不是作为候选集存在。是作为下一轮的候选点
        Backtrack(cur->left, sum - cur->val, path, res);
        Backtrack(cur->right, sum - cur->val, path, res);
        path.pop_back(); // 撤销cur
    }

124. 二叉树中的最大路径和(h)

  思路：递归(从下到上求最值，递归函数需要返回值)： 路径可以从任意节点开始到任意节点结束。最终的最大值一定是在横向检查完才能知道。横向检查完就是(cur->val, cur->lUniPathAttiVal, cur->rUniPathAttiVal)三个值检查一遍，是否累加起来最大。

   // 唯一路径对一个cur节点来说在不同的场景是有不同的作用的：

    // 一个cur节点的唯一路径对父贡献值: 贡献是对cur的父节点的贡献，只能携带着lUniPathAttiVal或rUniPathAttiVal或不携带

    //                              = max(lUniPathAttiVal, rUniPathAttiVal) > 0 ? cur->val + max(lUniPathAttiVal, rUniPathAttiVal) : cur->val;

    // 包含cur节点的唯一路径最大值: 若lUniPathAttiVal和rUniPathAttiVal均大于0, 那么对cur来说就是真有贡献的, 所以cur总共的贡献值是 cur->val + lefttreeval + righttreeval

    //                          = cur->val + max(cur->left节点的唯一路径对父贡献值, 0) + max(cur->right节点的唯一路径对父贡献值, 0)

class Solution {
public:
    // 唯一路径对一个cur节点来说在不同的场景是有不同的作用的：
    // 一个cur节点的唯一路径对父贡献值: 贡献是对cur的父节点的贡献，只能携带着lUniPathAttiVal或rUniPathAttiVal或不携带
    //                              = max(lUniPathAttiVal, rUniPathAttiVal) > 0 ? cur->val + max(lUniPathAttiVal, rUniPathAttiVal) : cur->val;
    // 包含cur节点的唯一路径最大值: 若lUniPathAttiVal和rUniPathAttiVal均大于0, 那么对cur来说就是真有贡献的, 所以cur总共的贡献值是 cur->val + lefttreeval + righttreeval
    //                          = cur->val + max(cur->left节点的唯一路径对父贡献值, 0) + max(cur->right节点的唯一路径对父贡献值, 0)
    int maxPathSum(TreeNode* root) {
        maxPathVal = INT_MIN;
        maxPathSumBtT(root);
        return maxPathVal;
    }
    int maxPathSumBtT(TreeNode* cur)
    {
        if (cur == nullptr) {
            return 0;
        }
        int lUniPathAttiVal = maxPathSumBtT(cur->left);
        int rUniPathAttiVal = maxPathSumBtT(cur->right);

        // 包含cur节点的唯一路径最大值 = cur->val + max(cur->left节点的唯一路径对父贡献值, 0) + max(cur->right节点的唯一路径对父贡献值, 0)
        int curIntitude = cur->val;
        if (lUniPathAttiVal > 0) {
            curIntitude += lUniPathAttiVal;
        }
        if (rUniPathAttiVal > 0) {
            curIntitude += rUniPathAttiVal;
        }
        // 更新最大值
        maxPathVal = max(maxPathVal, curIntitude);
        // cur节点的唯一路径对父贡献值
        return max(lUniPathAttiVal, rUniPathAttiVal) > 0 ? cur->val + max(lUniPathAttiVal, rUniPathAttiVal) : cur->val;
    }
private:
    int maxPathVal = 0;
};

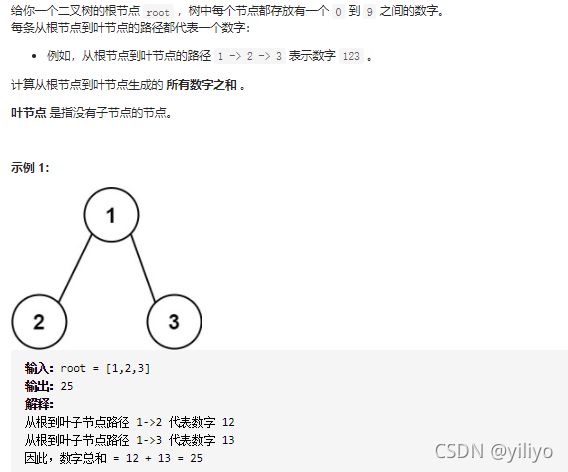
129. 求根节点到叶节点数字之和(m)

    //思路：回溯（利用路径求路径和(非最值)）：path传参用于自动撤销候选点

    // 二叉树回溯：回溯函数中以cur为候选点，而不是left和right为候选集。left和right是回溯函数递归到下一轮时的cur候选点

    //思路：回溯：path传参用于自动撤销候选点
    // 二叉树回溯：回溯函数中以cur为候选点，而不是left和right为候选集。left和right是回溯函数递归到下一轮时的cur候选点
    int sumNumbers(TreeNode* root) {
        int sum = 0;
        if (root == nullptr) {
            return sum;
        }
        int path = 0;
        Backtrack(root, path, sum);
        return sum;
    }
    void Backtrack(TreeNode* cur, int path, int &sum)
    {
        // 终止
        if (cur == nullptr) {
            return;
        }
        // 候选点cur选入path
        path = path * 10 + cur->val;
        // 收敛
        if (cur->left == nullptr && cur->right == nullptr) {
            sum += path;
        }

        Backtrack(cur->left, path, sum);
        Backtrack(cur->right, path, sum);
        // 恢复现场: 参数传值，非引用. 函数return时,path中自动会撤回cur->val
    }

二叉树递归与回溯框架的选用：

1，递归(dfs)（从下到上，从上到下）

偏向于求最值，或纯遍历树。没有明显的利用从root到left路径的概念。

特点：

(1) 递归函数一般需要返回一个值(非bool)，偏向求最值(深度、最大路径和)或二叉树构建。

(2) 递归函数没有返回值的递归，一般偏纯遍历。

2，回溯

有明显的利用从root到left路径进行：求解的个数、求是否有解（递归函数返回bool）、求路径和(非最值)。

特点：

（1）因为有明显路径的概念，需要有候选点加入path和恢复现场的动作。