恒者走天下
恒者走天下

《代码随想录》一刷记录

文章目录

  • 前言
  • 二、程序的性能分析
      • 时间复杂度分析
            • 递归算法的时间复杂度分析
      • 编程语言的内存管理
            • 内存对齐
      • 空间复杂度分析
            • 递归算法的空间复杂度分析
      • 以空间换时间是常见的优化思路
  • 三、数组
      • 二分查找
      • 移除元素
      • 长度最小的子数组
      • 螺旋矩阵
  • 四、链表
      • 链表的定义
      • 移除链表元素
      • 链表常见的操作
      • 反转链表
      • 删除倒数第n个节点
      • 环形链表
  • 五、哈希表
      • 哈希碰撞
      • 有效的字母异位词
      • 两个数组的交集
  • 六、字符串
      • 反转字符串
      • 反转字符串
      • 反转字符串里的单词
      • KMP算法
  • 七、栈和队列
      • 用栈组成队列
      • 用队列组成栈
            • 使用两个队列实现栈
            • 使用一个队列实现栈
      • 匹配括号
      • 逆波兰表达式
      • 滑动窗口最大值
      • 前k个高频元素
      • 接雨水
            • 双指针解法
      • 动态规划解法
      • 单调栈解法
  • 八、二叉树
      • 二叉树种类
      • 二叉树的遍历方式
      • 二叉树定义
      • 前、中、后序的递归遍历
      • 前、中、后序的迭代遍历
            • 二叉树的前序遍历
            • 中序遍历
            • 后序遍历
      • 前、中、后序统一迭代法
      • 二叉树的层序遍历
      • 反转二叉树
            • 递归法
            • 迭代法
      • 对称二叉树
            • 递归法
            • 迭代法
      • 二叉树的最大深度
            • 递归法
      • 迭代法
      • 二叉树的最小深度
            • 递归法
      • 迭代法
      • 平衡二叉树
            • 递归法
            • 迭代法
      • 二叉树的所有路径
            • 递归法
      • 迭代法
      • 路径总和
            • 递归法
            • 迭代法
      • 路径总和 II
      • 构造一棵二叉树
            • 使用中序与后序遍历序列构造二叉树
            • 使用前序与中序遍历序列构造二叉树
      • 合并两棵二叉树
            • 递归法
            • 迭代法
      • 在二叉搜索树中寻找节点
            • 递归法
            • 迭代法
      • 验证二叉搜索树
      • 递归法
            • 迭代法
      • 二叉搜索树的最小绝对差
            • 递归法
            • 迭代法
      • 二叉搜索树
            • 递归法
            • 迭代法
      • 二叉树的最近公共祖先
            • 普通二叉树
            • 二叉搜索树
      • 在二叉搜索树中插入一个节点
            • 递归法
            • 迭代法
      • 在二叉搜索树中删除一个节点
            • 递归法
            • 迭代法
      • 修剪二叉搜索树
            • 递归法
            • 迭代法
      • 构造一棵平衡二叉搜索树
            • 递归法

前言

算法毋庸置疑找工作必考的，为了提升自己的算法能力。同时也了解到一些学长面试时候遇到的算法题，在《代码随想录》中很多都有介绍，因此，打算通过《代码随想录》这本书，来系统的提升下自己的算法编程能力。此篇，乃是一刷的笔记记录。1-----8章

二、程序的性能分析

时间复杂度分析

在决定使用哪些算法时，不是时间复杂度越低越好（因为简化后的时间复杂度忽略了常数项等），还要考虑数据规模，如果规模很小，那么可能出现时间复杂度为O（n^2）的算法比时间复杂度为O（n）的算法更合适的情况（在有常数项的时候）

递归算法的时间复杂度分析

下面通过简单的测试题，来分析递归算法的时间复杂度：
求x的n次方
最直观的方法是for循环得出结果：

int function1(int x,int n)
{
	int result=1;
	for(int i=0;i<n;i++)
	{
		result=result*x;
	}
	return result;
}

时间复杂度为O（n）不是最优的，下面进行优化。
认识到递归算法可以对上面进行优化。
便写下下面的递归算法：

int function2(int x,int n)
{
	if(n==0)
		return 1;
	return function2(x,n-1)*x;
}

递归算法的时间复杂度本质上要看递归的次数与每次递归中的操作次数的乘积。 上面的程序递归了n次，并且乘法操作的时间复杂度是一个常数项O(1),所以上面程序的时间复杂度为O（n）。并没有优化。
于是写下了下面又写下了下面代码：

int function3(int x,int n)
{
	if(n==0)
		return 1;
	if(n%2==1)
		return function3(x,n/2)*function3(x,n/2)*x;
	return function3(x,n/2)*function3(x,n/2);
}

看这个程序的时间复杂度，首先要看递归的次数，可以把递归的次数抽象为一颗满二叉树，这个二叉树的每一个节点就代表一次递归并执行了一次相乘操作，所以看执行了多少次递归操作，就是看这颗树上有多少个节点。
通过举例得出，这个程序的时间复杂度仍为O（n）。
于是写下下面的代码程序

int function4(int x,int n)
{
	if(n==0)
		return 1;
	int t=function4(x,n/2);
	if(n%2==1)
		return t*t*x;
	return t*t;
}

这里仅有一个递归调用，而且每次递归操作的数据规模都除以2，所以这里一共调用了log2 n,时间复杂度是真正的O(logn)。

编程语言的内存管理

以c++为例介绍编程语言的内存管理。程序运行时所需的内存空间分为固定部分和可变部分。
固定部分：代码区（存储二进制代码）、数据区（全局变量、静态变量、常量等），固定部分的内存消耗不会随着代码运行而产生变化，而可变部分会产生变化。
可变部分：

  • 栈区（stack）：由编辑器自动分配释放，存放函数的参数值、局部变量等，其操作方法类似于数据结构中的栈。
  • 堆区(heap):一般由程序员分配释放，若程序员不释放，则程序结束时可能由系统收回。
内存对齐

为什么会有内存对齐？
主要原因如下：
（1）平台原因：不是所有的硬件平台都能访问任意内存地址上的数据，某些平台只能在一些地址处获取特定类型的数据，否则抛出硬件异常。为了使同一个程序可以在多平台运行，需要进行内存对齐。
（2）硬件原因：经过内存对齐后，CPU访问内存的速度会大大提升。

看下面程序：

struct node
{
	int num;
	char cha;
}st;
int main()
{
	cout<<sizeof(st)<<endl;
}

在这里插入图片描述
此时发现，输出的结果和单纯计算字节数是有一些误差的，这就是执行内存对齐的效果。
下面分析内存对齐和非内存对齐产生的效果的区别：
CPU读取内存时不是一次读取单个字节，而是按照块来读取的，块的大小可以是2、4、 8、 16字节，具体读取多少字节取决于硬件。
假设CPU把内存划分为4字节大小的块，要读取一份4字节大小的int型数据，来看下两种情况下CPU的工作量。
第一种是内存对齐的情况，如下图：
《代码随想录》一刷记录_第1张图片
1字节的char占用了4字节的内存空间，空了3字节的内存地址，int数据从地址4开始。此时，直接读取地址4、 5、 6、 7处的4字节数据即可。

第二种是非内存对齐的情况，如下图：
《代码随想录》一刷记录_第2张图片
char型数据和int型数据挨在一起，该int型数据从地址1开始，CPU读取这个数据需要如下几步操作：
（1） CPU读取0、 1、 2、 3处的4字节的数据；
（2） CPU读取4、 5、 6、 7处的4字节的数据；
（3） 合并地址1、 2、 3、 4处后的4字节的数据才是本次操作需要的int型数据。
此时一共需要两次寻址、一次合并的操作。

空间复杂度分析

空间复杂度两个常见的相关问题：
（1）空间复杂度考虑程序（可执行文件）的大小吗？
空间复杂度考虑的是程序运行时占用内存的大小，而不是可执行文件的大小。
（2）空间复杂度可以准确计算出程序运行时占用的内存值吗？
很多因素会影响程序真正使用的内存大小，例如，编辑器的内存对齐，编程语言容器的底层实现等都会影响程序内存的开销。所以空间复杂度仅仅是预先大致评估程序内存使用的大小。

递归算法的空间复杂度分析

以递归求斐波那契数列为例：

int fibonacci(int i)
{
	if(i<=0)	return 0;
	if(i==1)	return 1;
	return 	fibonacci(i-1)+fibonacci(i-2);
}

递归算法的空间复杂度=每次递归的空间复杂度*递归深度
为什么要求递归深度？
因为每次递归所需要的空间都被压到调用栈里，一次递归结束，这个栈就把本次递归的数据“弹出去”。所以这个栈的最大长度就是递归的深度。
因此分析得出，空间复杂度为O（n），时间复杂度为O（2^n）。

优化：

int fibonacci(int first,int second,int n)
{
	if(n<=0)	return 0;
	if(n<3)		return 1;
	else if(n==3)
		return first+second;
	else
		return fibonacci(second,first+second,n-1);
}

空间复杂度依然是O（n），时间复杂度是O（n）。

以空间换时间是常见的优化思路

以例题为例：给出n个字母（小写字母从a到z），找出出现次数最多的字母并输出该字母。
最先想到的就是使用两层for循环枚举出现次数最多的字母，

void solution(const vector<char> &a)
{
	char result;
	int max_count=0;
	for(int i=0;i<a.size();i++)
	{
		int num=0;
		for(int j=0;j<a.size();j++)
		{
			if(a[i]==a[j])
				num++;
		}
		if(num>max_count)
		{
			result=a[i];
			max_count=num;
		}
	}
	cout<<"出现最多的字母是"<<result<<"出现次数"<<max_count<<endl;
}

时间复杂度O（n^2），时间复杂度O（1）；
优化：
这里可以基于以空间换时间思路，使用一个数组记录字母出现了多少次。因为题目中要求字母都是小写字母，所以可以设定一个长度为26的数组（因为有26个字母）。这样只需一次遍历，代码如下

void solution_1(const vector<char> &a)
{
	int record[26]={0};
	for(int i=0;i<a.size();i++)
	{
		record[a[i]-'a']++; //用字符的ASCII码来做运算
	}
	char result;
	int max_count=0;
	for(int i=0;i<26;i++)
	{
		if(record[i]>max_count)
		{
			max_count=record[i];
			result=i+'a';
		}
	}
	cout<<"出现最多的字母是"<<result<<"出现次数"<<max_count<<endl;
}

时间复杂度O（n），空间复杂度O(1);

三、数组

使用c++，注意vector和array的区别，vector的底层实现其实就是array。

二分查找

题目描述：
在一个有序无重复元素的数组nums中，寻找一个元素target，如果找到了就返回对应的下标，如果没找到就返回-1。（力扣题号704）

思路：
二分法中区间的定义一般有两种，一种是左闭右闭即[left,right]，另一种是左闭右开即[left,right)。下面基于这两种区间的定义分别讲解两种不同的二分写法

  1. 二分写法（一）
    定义target在一个左闭右闭的区间，也就是[left,right]。
    因为定义target在[left，target]区间（左闭右闭），所以有如下两点：
  • 因为left与right相等的情况在[left,right]区间是有意义的，所以在while（left<=right）中要使用<=。
  • 如果nums[middle]大于target，则更新搜索范围右下标right为middle-1。因为当前这个nums[middle]一定不是target，所以接下来要查找的左区间结束下标位置是middle-1。
    代码如下：
int search(vector<int>& nums,int target)
{
	int left=0;
	//定义target在左闭右闭的区间，即[left,right]
	int right=nums.size()-1;
	while(left<=right)
	{
		//防止溢出，等同于(left+right)/2
		int middle=left+((right-left)/2);
		if(nums[middle]>target)
			right=middle-1;
		else if(nums[middle]<target)
			left=middle+1;
		else
			return middle;
	}
	return -1;
}
  1. 二分法写法（二）
    定义target在一个左闭右开的区间，也就是[left,right）。
    因为定义target在[left，target)区间（左闭右开），所以有如下两点：
  • while（left
  • 如果nums[middle]大于target，则更新搜索范围右下标right为middle。因为当前nums[middle]不等于target，那么去左区间继续寻找，而寻找的区间是左闭右开区间，所以right更新为middle，即在下一个查询区间不会比较nums[middle]。

代码如下：

int search(vector<int>& nums,int target)
{
	int left=0;
	//定义target在左闭右开的区间，即[left,right)
	int right=nums.size();
	while(left<right)
	{
		int middle=left+((right-left)/2);
		if(nums[middle]>target)
			right=middle;
		else if(nums[middle]<target)
			left=middle+1;
		else
			return middle;
	}
	return -1;
}

移除元素

题目描述：
原地移除数组中所有等于val的元素，要求不能使用额外的辅助空间，即空间复杂度为O（1）。返回移除元素后新数组的size。（力扣题号27）

  1. 暴力解法
    使用两个for循环，第一个for循环遍历数组元素，第二个for循环更新数组，移除元素的过程。
    代码如下：
int removeElement(vector<int>& nums,int val)
{
	int size=nums.size();
	for(int i=0;i<size;i++)
	{
		if(nums[i]==val) //发现相等元素都向前移动
		{
			for(int j=i+1;j<size;j++)
			{
				nums[j-1]=nums[j];
			}
			i--;
			size--;
		}
	}
	return size;
}

时间复杂度O（n^2）;空间复杂度O（1）

  1. 双指针法
    双指针法（快慢指针法）：通过一个快指针和慢指针在一个for循环内完成两个for循环的工作。
    代码如下：
int removeElement(vector<int>& nums,int val)
{
	int slowindex=0;
	for(int fastIndex=0;fastIndex<nums.size();fastIndex++)
	{
		if(val!=nums[fastIndex])
		{
			nums[slowIndex++]=nums[fastIndex];
		}
	}
	return slowIndex;
}

时间复杂度O（n）；空间复杂度O（1）

长度最小的子数组

题目描述：
在一个正整数数组nums中找到最小长度的连续子数组，使子数组元素之和大于或等于s。返回满足条件的连续子数组的最小长度，如果没找到则返回0。（力扣题号209）

  1. 暴力解法
    使用两个for循环，不断地寻找符合条件的子数组。
    代码如下：
int minSubArrayLen(int s,vector<int>& nums)
{
	int result=INT32_MAX; //最终结果
	int sum=0;//子数组的元素之和
	int sublength=0; //子数组的长度
	for(int i=0;i<nums.size();i++)
	{
		sum=0;
		for(int j=i;j<nums.size();j++)
		{
			sum+=nums[j];
			if(sum>=s)
			{
				sublength=j-i+1;
				result=result<sublength ? result:sublength;
				break;
			}
		}
	}
	return result==INT32_MAX ? 0:result;
}

时间复杂度O（n^2）;空间复杂度O（1）。

  1. 滑动窗口
    滑动窗口，就是不断地调节子数组的起始位置和终止位置，得到想要的结果。
    实现滑动窗口是要确定以下三点？
    窗口内的元素、 移动窗口的起始位置、 移动窗口的终止位置

代码如下：

int minSubArrayLen(int s,vector<int>& nums)
{
	int result=INT32_MAX;
	int sum=0;//滑动窗口的数值之和
	int i=0;//滑动窗口的起始位置
	int sublength=0;//滑动窗口的长度
	for(int j=0;j<nums.size();j++)
	{
		sum+=nums[j];
		while(sum>=s)
		{
			sublength=j-i+1;
			result=result<sublength ? result : sublength;
			//不断变更i(子数组的起始位置)来实现窗口的移动
			sum -=nums[i++];
		}
	}
	return result==INT32_MAX ? 0: result;
}

时间复杂度O(n);空间复杂度O(1)

螺旋矩阵

题目描述：
给出一个正整数n，按从外向内的螺旋顺序打印1到n^2的所有数值。
《代码随想录》一刷记录_第3张图片
循环不变量原则
矩阵的四条边都要坚持一致的左闭右开或者左开右闭的原则，这样才能按照统一的规则“画”下来
按照左闭右开的原则“画圈”，如下图
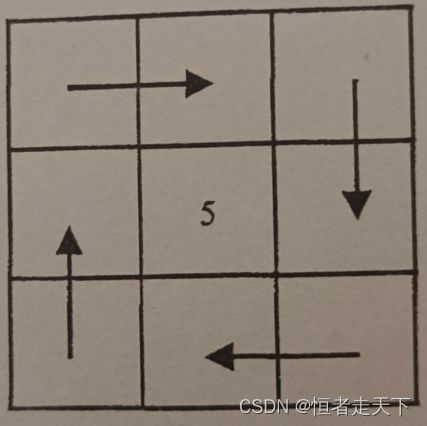
《代码随想录》一刷记录_第4张图片
每一个箭头覆盖的长度表示一条边遍历的长度，可以看出每一个拐角处的处理规则，在拐角处画一条新的边。
代码如下：

vector<vector<int>> generateMatrix(int n)
{
	vector<vector<int>> res(n,vector<int>(n,0));
	int startx=0,starty=0;//定义每循环一个圈的起始位置
	int loop=n/2;//每个圈循环的次数
	int mid=n/2; //矩阵中间的位置
	int count=1; //用来给矩阵中每一个空格赋值
	int offset=1; //每一圈循环都需要控制每一条边遍历的长度
	int i,j;
	while(loop--)
	{
		i=startx;
		j=starty;
		
		//下面开始的4个for就是模拟转了一圈
		//模拟填充上行从左到右（左闭右开）
		for(j=starty; j<starry+n-offset;j++)
		{
			res[startx][j]=count++;
		}
		//模拟填充右列从上到下（左闭右开）
		for(i=startx;i<startx+n-offset;i++)
		{
			res[i][j]=count++;
		}
		//模拟填充下行从右到左（左闭右开）
		for(;j>starty;j--)
		{
			res[i][j]=count++;
		}
		//模拟填充左列从下到上（左闭右开）
		for(;i>startx;i--)
		{
			res[i][j]=count++;
		}
		//第二圈开始的时候，起始位置要各自加1
		//例如：第一圈的起始位置是(0,0)，第二圈的起始位置是(1,1)
		startx++;
		starty++;
		//offset用于控制每一圈中每一条边遍历的长度
		offset+=2;
	}
	//如果n为奇数，则需要单独给矩阵最中间的位置赋值
	if(n%2)
		res[mid][mid]=count;
	return res;
}

四、链表

链表的定义

//单链表
struct ListNode
{
	int val;
	ListNode *next;
	ListNode(int x): val(x),next(nullptr){ } //节点的构造函数
};

自己在结构体中定义构造函数，有利于初始化节点。
通过自定义构造函数初始化节点：

ListNode *head=new ListNode(5);

使用默认构造函数初始化节点：

ListNode *head=new ListNode();
head->val=5;

移除链表元素

题目描述：
在链表中删除指定的元素。（力扣题号203）

对头结点删除比较特殊
代码如下：

ListNode* removeElements(ListNode *head,int val)
{
	//删除头节点
	while(head !=NULL && head->val==val)
	{
		ListNode *temp=head;
		head=head->next;
		delete temp;
	}
	ListNode *cur=head;
	while(cur !=NULL && cur->next !=NULL)
	{
		if(cur->next->val==val)
		{
			ListNode *temp=cur->next;
			cur->next=cur->next->next;
			delete temp;
		}
		else
		{
			cur=cur->next;
		}
	}
	return head;
}

使用统一的逻辑来进行删除，不用对头节点进行特殊判断。设置虚拟头节点
代码如下：

ListNode* removeElements(ListNode *head,int val)
{
	ListNode *dummyHead=new ListNode(0);//设置一个虚拟头节点
	dummyHead->next=head;
	
	ListNode *cur=dummyHead;
	while(cur->next !=NULL)
	{
		if(cur->next->val==val)
		{
			ListNode *temp=cur->next;
			cur->next=cur->next->next;
			delete temp;
		}
		else 
			cur=cur->next;
	}
	head=dummyHead->next;
	delete dummyHead;
	return head;
}

链表常见的操作

题目描述：
设计一个链表类，实现六个接口：
1 获取链表的第index个节点的数值
2 在链表的最前面插入一个节点
3 在链表的最后面插入一个节点
4 在链表的第index个节点前面插入一个节点
5 删除链表的第index个节点
6 打印当前链表 （力扣题号707）

代码如下：

class MyLinkedList
{
	private:
		int size;
		LinkNode *head;//含有空值的头节点
	public:
		struct LinkNode
			{
				int val;
				LinkNode *next;
				LinkNode(int val): val(val),next(nullptr){ };
			};
		//初始化链表
		MyLinkedList()
		{
			//虚拟头节点
			head=new LinkNode(0);
			size=0;
		}
		//获取第index个节点的数值
		int get(int index)
		{
			if(index<0 || index>(size-1)
				return -1;
			LinkNode *cur=head->next;
			for(int i=0;i<=index;i++)
				cur=cur->next;
			return cur->val;
		}
		//在链表最前面插入一个节点
		void addHead(int val)
		{
			LinkNode *newcur=new LinkNode(val);
			newcur->next=head->next;
			head->next=newcur;
			size++;
		}
		//在链表最后面添加一个节点
		void addTail(int val)
		{
			LinkNode *newcur=new LinkNode(val);
			LinkNode *cur=head->next;
			while(cur->next!=nullptr)
			{
				cur=cur->next;
			}
			cur->next=newcur;
			size++;
		}
		//在第index个节点之前插入一个新节点
		void addIndex(int index,int val)
		{
			if(index>size)
				return -1;
			//LinkNode *cur=head->next;
			LinkNode *cur=head
			while(index--)//到达index节点的前一个节点
			{
				cur=cur->next;
			}
			LinkNode *newcur=new LinkNode(5);
			newcur->next=cur->next;
			cur->next=newcur->next;
			size++;
	
		}
		//删除第index个节点
		void deleteIndex(int index)
		{
			if(index>=size || index<0)
				return ;
			LinkNode *cur=head;
			while(index--)//到达index节点的前一个节点
			{
				cur=cur->next;
			}
			LinkNode *del=cur->next;
			cur->next=cur->next->next;
			delete del;
			size--;
		}
		//打印链表
		void printLinkList()
		{
			LinkNode *cur=head->next;
			while(cur!=nullptr)
			{
				cout<<cut->val<<endl;
				cur=cur->next;
			}
		}
};

反转链表

题目描述：
反转一个单链表。要求是不能申请额外的内存空间。

  1. 双指针法
    代码如下：
LinkNode* reverseList(ListNode* head)
{
	LinkNode *temp;//保存下一个节点
	LinkNode *cur=head;
	LinkNode *pre=nullptr;
	while(cur)
	{
		temp=cur->next;
		cur->next=pre;
		pre=cur;
		cur=temp;
	}
	return pre;
}
  1. 递归算法
    代码如下：
LinkNode* reverse(ListNode* pre,ListNode* cur)
{
	if(cur==nullptr)
		return pre;
	LinkNode *temp=cur->next;
	curt->next=pre;
	//可以和双指针法的代码进行对比，如下递归的写法，其实就是为了做这两步
	// pre=cur;
	// cur=temp;
	reverse(cur,temp);
}
LinkNode* reverseList(ListNode *head)
{
	return reverse(nullptr,head);
}

删除倒数第n个节点

题目描述：
删除链表的倒数第n个节点（力扣题号19）

思路：
双指针的经典应用，如果要删除倒数第n个节点，则让fast移动n步，然后fast和slow同时移动，直到fast指向链表末尾，删除slow所指向的节点就可以了

代码如下：

ListNode* removeNthFromEnd(ListNode *head,int n)
{
	ListNode *dummyHead=new ListNode(0);
	dummyHead->next=head;
	ListNode *fast=dummyHead;
	ListNode *slow=dummyHead;
	
	while(n-- && fast!=nullptr)
	{
		fast=fast->next;
	}
	//fast再提前移动一步，因为需要让slow指向删除节点的上一个节点
	fast=fast->next;
	while(fast!=nullptr)
	{
		fast=fast->next;
		slow=slow->next;
	}
	slow->next=slow->next->next;
	return dummyHead->next;
}

注意函数的返回值必须是dummyHead->next,不能是head。因为如果链表中只有一个元素，并且只把这个元素移除，那么如果返回的是head，程序的输出还是没变，有错误。如下面测试用例：
《代码随想录》一刷记录_第5张图片

环形链表

题目描述：
判断一个链表是否有环，如果有环，则找到入环的第一个节点，如果无环，则返回NULL。（力扣142）

思路：
这个题其实有两问。

  1. 链表是否有环
    快慢指针法，fast指针每次移动两步，slow指针每次移动一步。如果有环，则两者会在途中相遇。
  2. 寻找环的入口
    看下图：
    《代码随想录》一刷记录_第6张图片
    设头节点到入口节点的节点个数为x，入口节点到相遇节点的节点个数为y，从相遇节点再到入口节点的节点个数为z。
    数学知识易知，两个指针一定在slow指针在环内一圈的时候相遇。
    因此可以得出数学关系式：
    fast指针移动的节点数=slow移动的节点数*2
    即（x+y）*2=x+y+n(y+z) (n代表fast指针在环内移动了n圈才遇到slow指针）
    寻找环的入口，就是求x
    化简得，x=（n-1） *（y+z）+z （n>=1,因为fast至少移动一圈后，才会和slow相遇）
    看上面的化简式，如果n=1，即x=z，这意味着，一个指针从头节点出发，另一个指针从相遇节点出发，这两个指针每次一起只移动一个节点，那么这两个指针相遇的节点就是环的入口节点
    如果n>1,其实和n=1一样，只不过在相遇节点的那个指针先在环内多移动了n-1圈，才能和从都节点出发的指针相遇。（这里在相遇节点处定义一个指针index1，在头节点处定义一个指针index2）。

代码如下：

ListNode* detectCycle(ListNode *head)
{
	ListNode *fast=head;
	ListNode *slow=head;
	while(fast !=nullptr && fast->next!=nullptr)
	{
		fast=fast->next->next;
		slow=slow->next;
		if(fast==slow)
		{
			ListNode *index1=fast;
			ListNode *index2=head;
			while(index1!=index2)
			{
				index1=index1->next;
				index2=index2->next;
				
			}
			return index1;
		}
	}
	return nullptr;
}

注意在判读是否有环时的循环条件，while(fast!=nullptr && fast->next!=nullptr)中fast->next!=nullptr不能省略，如果省略，对于链表中只有一个元素的链表，fast=fast->next->next会报错。 如下测试用例
《代码随想录》一刷记录_第7张图片

五、哈希表

哈希表能解决什么问题呢？
哈希表一般用来快速判断一个元素是否出现在集合中。

哈希碰撞

  1. 拉链法
    选择适当的哈希表大小，这样即不会因为数组空值而浪费大量内存，也不会因为链表太长而在查找上浪费太多时间。
  2. 线性探测法
    哈希表大小大于数据规模

有效的字母异位词

题目描述：
判断字符串s中的字符是否可以通过改变顺序的方式变成字符串t（如果字符串s与字符串t相同，那么也是可以的）。字符串中只包含小写字母。（力扣242）

思路：
数组就是简单的哈希表。将定义一个数组（因都是小写字母，并且字母一共才有26个，因此定义数组的长度为26），将字符映射到这个数组上，映射到的位置元素值加1，另一个字符串也映射到该数组上，映射到的位置元素值减1。 看最后，该数组上的元素是否都为0，是则可以，不是则不可以。

代码如下：

bool isAnagram(string s,string t)
{
	int index[26]={0};
	for(int i=0;i<s.size();i++)
	{
		//通过ASCII进行映射
		index[s[i]-'a']++;
	}
	for(int i=0;i<t.size();i++)
	{
		index[t[i]-'a']--;
	}
	for(int i=0;i<26;i++)
	{
		if(index[i]!=0)
		{
			return false;
		}
	}
	return true;
}

两个数组的交集

题目描述：
计算两个数组的交集，交集里的元素都是唯一的（力扣349）

思路：
输出结果中的每个元素一定是唯一的，结果去重，并且不需要考虑输出结果的顺序。
用哈希数据结构unordered_set读写效率是最高的

代码如下：

vector<int> intersection(vector<int>& nums1,vector<int>& nums2)
{
	unordered_set<int> result_set;//结果集
	unordered_set<int> nums_set(nums1.begin(),nums1.end());
	for(int num : nums2)
	{
		if
	}
}

六、字符串

反转字符串

题目描述：
将一个字符串反转（力扣344）

思路：
双指针法，一个在字符串头，一个在字符串尾。不断交换两者的值即可

代码如下：

void reverseString(vector<char> &s)
{
	for(int i=0,j=s.size()-1;i<s.size()/2;i++,j--)
	{
		char t;
		t=s[i];
		s[i]=s[j];
		s[j]=t;
	}
}

反转字符串

题目描述：
分段反转字符串，在字符串中，从前向后遍历，每隔2k个字符的前k个字符需要反转，如果剩下的字符小于k个，则反转剩下的所有字符，如果剩下的字符小于2k且大于或等于k个，则反转前k个字符。（力扣541）

思路：
题目中要找的是每个2k区间的起点，在遍历字符串的过程中，只要让i+=(2k),i每次移动2k，然后判断是否有需要反转的区间即可。

代码如下：

string reverseStr(string s,int k)
{
	for(int i=0;i<s.size();i+=(2*k))
	{
		/*if(i+k<=s.size())
		{
			reverse(s.begin()+i,s.begin()+i+k);
			continue;
		}*/
		//i+k<=size()说明剩下的字符大于等于k
		if(i+k<=s.size())
		{
			int z=0;
			int m=i;
			for(int j=(m+k-1);z<(k/2);m++,j--,z++)
			{
				char temp;
				temp=s[m];
				s[m]=s[j];
				s[j]=temp;
			}
			continue;
		}
		reverse(s.begin()+i,s.begin()+s.size());
	}
	return s;
}

自己把reverse(s.begin()+i,s.begin()+i+k);用for循环来代替，注意必须要用m代替i，因为如果不用m代替i，则这里i++设计到了i值的变化，再在上面的大循环里i已经变了，程序出错了。

反转字符串里的单词

题目描述：
给定一句英文，要求倒叙输出每一个单词，并删除单词两边冗余的空格（句子前面和后面没有空格，两个单词之间没有空格）。注意：不可以使用额外的辅助空间，即原地修改字符串。（力扣151）

思路：
不使用辅助空间。可以先将整个字符串都反转过来，那么单词的顺序指定是倒序的了，再把单词“正”过来就可以了。
具体方法：
（1）删除多余空格；（2）将整个字符串反转；（3）将每个单词反转
使用双指针法删除空格，最后重新设置（resize）字符串的大小，就可以实现O（n）的时间复杂度了
注意此题两个字符串之间可能有多个空格，空格数>=1
删除冗余空格的代码如下：

void removeExtraSpaces(string &s)
{
	int slowIndex=0,fastIndex=0; //定义快指针和慢指针
	//去掉字符串前面的空格
	while(s.size()>0 && fastIndex<s.size() && s[fastIndex]==' ')
	{
		fastIndex++;
	}
	//去掉字符串中间部分冗余的空格（意思是说，原输入的字符串两个单词之间的空格数量可能不是一个，而是两个或多个）
	for(;fastIndex<s.size();fastIndex++)
	{
		if((fastIndex-1)>0 && s[fastIndex-1]==s[fastIndex] && s[fastIndex]==' ')
		{
			continue;
		}
		else
		{
			s[slowIndex++]=s[fastIndex];
		}
	}
	//去掉字符串末尾的空格
	if(slowIndex-1>0 && s[slowIndex-1]==' ')
	{
		s.resize(slowIndex-1);
	}
	else
	{
		s.resize(slowIndex); //重新设置字符串的大小
	}
}

整体代码如下：

//反转字符串s中左闭右闭的区间[start,end]
void reverse(string &s,int start,int end)
{
	for(int i=start,j=end;i<j;i++,j--)
	{
		swap(s[i],s[j]);
	}
}

//删除冗余空格：使用双指针（快慢指针法），时间复杂度为O（n）的算法
void removeExtraSpace(string &s)
{
	int slowIndex=0,fastIndex=0;//定义快指针、慢指针
	//去掉字符串前面的空格
	while(s.size()>0 && fastIndex<s.size() && s[fastIndex]==' ')
	{
		fastIndex++;
	}
	//去掉单词中间的冗余空格
	for(;fastIndex<s.size();fastIndex++)
	{
		//s.size()是为了排除空字符串
		if(s[fastIndex-1]==s[fastIndex] && s[fastIndex]==' ' && s.size()>0)
		{
			continue;
		}
		else
		{
			s[slowIndex++]=s[fastIndex];
		}
	}
	//去掉字符串末尾的空格
	//注意slowIndex表示现在字符串的长度和下标也是差个1
	//slowIndex-1>0字符串是空串或者只有一个字母，就没必要考虑冗余空格了
	if((slowIndex-1)>0 && s[slowIndex-1]==' ')
	{
		s.resize(slowIndex-1);
	}
	else 
	{
		s.resize(slowIndex);
	}
}

string reverseWords(string s)
{
	removeExtraSpace(s); //去掉冗余空格
	reverse(s,0,s.size()-1);//将字符串全部反转自定义函数闭区间
	int start=0;//反转的单词在字符串中的起始位置
	int end=0; //反转的单词在字符串中的终止位置
	bool entry=false; //标记枚举字符串的过程中是否已经进入单词区间
	
	//开始反转单词
	for(int i=0;i<s.size();i++)
	{
		//确定单词的起始位置
		if((!entry) || (s[i]!=' ' && s[i-1]==' '))
		{
			start=i;//确定单词起始位置
			entry=true; //进入单词区间
		}
		//确定单词的终止位置
		//单词后面有空格的情况，空格就是分词符
		if(entry && s[i]==' ' && s[i-1]!=' ')
		{
			end=i-1;//确定单词终止位置
			entry=false;//结束单词区间
			reverse(s,start,end);
		}
		//最后一个结尾单词之后没有空格的情况
		if(entry && (i==(s.size()-1)) && s[i]!=' ')
		{
			end=i;
			entry=false;
			reverse(s,start,end);
		}
	}
	return s;
}

KMP算法

七、栈和队列

用栈组成队列

题目描述：
使用两个栈实现队列的功能。 （力扣232）

思路：
使用栈模拟队列，仅用一个栈是不行的，需要两个栈，一个是输入栈，另一个是输出栈。
当有数据来的时候，直接push进输入栈即可。
当有数据要出来的时候，如果输出栈为空，则把输入栈数据全部导入输出栈中，如果输出栈不为空，则直接从输出栈中弹出数据即可。
如何判断队列为空？
如果输入栈和输出栈都为空，则说明模拟的队列为空了。

代码如下：

class MyQueue
{
	public:
		stack<int> stIn;
		stack<int> stOut;
		MyQueue()
		{
			
		}
		//从队尾添加元素
		void push(int x)
		{
			stIn.push(x);
		}
		//弹出队头元素
		int pop()
		{
			if(stOut.empty())
			{
				while(!stIn.empty())
				{
					stOut.push(stIn.top());
					stIn.pop();
				}
			}
			int result=stOut.top();
			stOut.pop();
			return result;
		}
		//获取队头元素
		int peek()
		{
			//此乃妙处，复用上面的pop()函数
			int res=this->pop();
			stOut.push(res);
			return res;
		}
		//判断队列是否为空
		bool empty()
		{
			/*if(stIn.empty() && stOut.empty())
			{
				return true;
			}
			return false;*/
			return stIn.empty() && stOut.empty();
		}
};

用队列组成栈

题目描述：
使用队列（单向队列）实现栈。

使用两个队列实现栈

其中一个队列用来存储数据，另一个队列充当中间存储(辅助队列，用来备份)。当要模拟出栈时，把存储数据的队列中除了最后一个元素，其他元素都转移到中间存储的队列中，然后输出最后一个元素，再移回去。

代码如下：

class MyStack
{
	public:
		queue<int> que1;
		queue<int> que2; //辅助队列，用来备份
		MyStack()
		{	}
		void push(int x)
		{
			que1.push(x);
		}
		int pop()
		{
			//将que1队列中只留下最后一个元素
			int size=que1.size();
			size--;
			while(size--)
			{
				que2.push(que1.front());
				que1.pop();
			}
			int result=que1.front();
			que1.pop();
			//把que2中的数据返回给que1，并把que2给清空
			que1=que2;
			while(!que2.empty())
			{
				que2.pop();
			}
			return result;
		}
		int top()
		{
			return que1.back();
		}
		bool empty()
		{
			return que1.empty();
		}
};
使用一个队列实现栈

使用一个队列也可以实现栈，在模拟栈弹出元素的时候只要将队列头部的元素（除了最后一个元素）重新添加到队列尾部，此时再弹出元素的顺序就是栈的顺序了。

代码如下：

class MyStack
{
	queue<int> que;
	MyStack()
	{ }
	void push(int x)
	{
		que.push(x);
	}
	int pop()
	{
		int size=que.size();
		size--;
		while(size--)
		{
			que.push(que.front());
			que.pop();
		}
		int result=que.front();
		que.pop();
		return result;
	}
	int top()
	{
		return que.back();
	}
	bool empty()
	{
		return que.empty();
	}
}

匹配括号

题目描述：
一个字符串只要有左括号“(”,就要有“)”来闭合，“{” “}” “[” “]”也同理。字符串只包含以上字符，判断字符串是否合法。(力扣20)

思路：
括号匹配是用栈解决的经典问题。
先来分析下不匹配的情况有几种：
（1）字符串中左方向的括号多余了，所以不匹配
（2）字符串中右方向的括号多余了，所以不匹配
（3）括号没有多余，但是括号类型不匹配
对应不匹配情况的判断方法：
（1）已经遍历了字符串，但是栈不为空，说明有相应的左括号，但没有右括号，返回错误
（2）在遍历字符串的过程中栈已经为空了，没有匹配的字符了，说明右括号没有找到对应的左括号，返回错误。
（3）在遍历字符串的过程中，发现栈中没有要匹配的字符，返回错误。

写代码的时候一个优化小细节：在匹配左括号的时候，右括号入栈，这样只需要比较当前元素和栈顶是否相等即可，比左括号先入栈的代码简单（判断语句直接用==简单哈哈）

代码如下:

bool isValid(string s)
{
	stack<char> st;
	for(int i=0;i<s.size();i++)
	{
		if(s[i]=='{')
			st.push('}');
		else if(s[i]=='(')
			st.push(')');
		else if(s[i]=='[')
			st.push(']');
		else if(st.empty() || st.top() !=s[i])
			return false;
		else
			st.pop();
	}
	return st.empty();
}

逆波兰表达式

题目描述：
给出逆波兰表达式，求得对应的值。（力扣150）

思路：
逆波兰表达式也称为一种不需要括号的后缀表达式（所有的符号都是在要运算数字的后面出现）
运算规则：从左到右遍历表达式的每个数字和符号，遇到是数字就进栈，遇到是符号，就将处于栈顶两个数字出栈，进行运算，运算结果进栈，一直到最终获得结果。

代码如下：

int evalRPN(vector<string> &tokens)
{
	stack<int> st;
	for(int i=0;i<tokens.size();i++)
	{
		if(tokens[i]=="+" || tokens[i]=="-" || tokens[i]=="*" || tokens[i]=="/")
		{
			int num1=st.top();
			st.pop();
			int num2=st.top();
			st.pop();
			if(tokens[i]=="+")
				st.push(num2+num1);
			else if(tokens[i]=="-")
				st.push(num2-num1);
			else if(tokens[i]=="*")
				st.push(num2*num1);
			else 
				st.push(num2/num1);
		}
		else 
			//stoi（字符串，起始位置，n进制）,将n进制的字符串转化为十进制
			st.push(stoi(tokens[i]));
	}
	int result=st.top();
	st.pop();
	return result;
}

注意±*/符号要用双引号，不能用单引号。否则报如下错误：
invalid operands to binary expression

滑动窗口最大值

题目描述：
一个大小为k的滑动窗口，从前向后在数组nums上移动，返回滑动窗口每移动一次时窗口中的最大值。
要求时间复杂度为：O（n） （力扣239）

思路：
实现一个单调队列，每次窗口移动时，调用que.pop(滑动窗口中移除的元素)、que.push（滑动窗口中添加的元素），然后que.front()返回队列中的最大值 。
并且队列中的元素需要排序，而且将最大值放在出队口，否则就不知道哪个是最大值。而且这个队列没有必要维护窗口中的所有元素，只需要维护有可能成为窗口中最大值的元素即可，同时保证队列的元素数值是由大到小排序的。
例如，对于窗口中的元素{2，3,5，1,4}，只维护{5,4}就够了。并且保持单调队列中的元素单调递减，此时队列出口的元素就是窗口中的最大元素。

设计单调队列的时候，pop和push操作保持如下规则：
（1）pop（）：如果窗口移除的元素value等于单调队列的出口元素，那么队列弹出元素，否则不进行任何操作。
（2）push（value）:如果push的元素value大于入口元素的数值，那么就将队列入口的元素弹出，直到push元素的数值小于或等于队列入口元素的数值。
基于以上规则，每次窗口移动的时候，只要调用que.front（）就可以返回当前窗口的最大值。

基于单调队列pop和push的规则，代码如下：

class MyQueue
{
	//单调队列（从大到小）
	deque<int> que;//使用deque实现单调队列
	//每次弹出元素时，比较当前要弹出的数值是否等于队列出口元素的数值，如果相等则弹出
	//弹出元素之前，需要判断队列当前是否为空
	void pop(int value)
	{
		if(!que.empty() && value==que.front())
			que.pop_front();
	}
	//如果push的数值大于入口元素的数值，那么就将队列入口的元素弹出，直到
	//push的数值小于或等于队列入口元素的值
	//这样就保持了队列中数值是从大到小单调递减的了
	void push(int value)
	{
		while(!que.empty() && value>que.back())
		{
			//可能出口的那个元素也会被弹出
			que.pop_back();
		}
		que.push_back(value);
	}
	//查询当前队列里的最大值，直接返回队列前端元素
	int front()
	{
		return que.front();
	}
};

完整代码如下：

class Solution
{
	private:
		class MyQueue
		{
			public:
				deque<int> que;
				void pop(int value)
				{
					if(!que.empty() && value==que.front())
						que.pop_front();
				}
				void push(int value)
				{
					while(!que.empty() && value>que.back())
					{
						que.pop_back();
					}
					que.push_back(value);
				}
				int front()
				{
					return que.front();
				}
	
		};
	public:
		vector<int>  maxSlidingWindow(vector<int> &nums,int k)
		{
			MyQueue que;
			vector<int> result;
			for(int i=0;i<k;i++)
			{  //先将前k个元素放入队列
				que.push(nums[i]);
			}
			//记录前k个元素的最大值
			result.push_back(que.front());
			for(int i=k;i<nums.size();i++)
			{
				que.pop(nums[i-k]);//
				que.push(nums[i]);
				result.push_back(que.front());
			}
			return result;
		}
		
};

前k个高频元素

题目描述：
在一个数组中找到出现频率前k高的元素

思路：
本题主要涉及3部分：（1）统计元素出现的次数 （2）对次数进行排序
(3）找出前k个高频元素

首先需要统计元素出现的次数，可以使用map进行统计；然后对次数进行排序，可以使用优先级队列，priority_queue(优先级队列）其实就是堆。
本题使用优先级队列对部分元素出现的次数进行排序。
为什么不使用快排？使用快排就要将map转换为vector的结构，然后对整个数组进行排序，而在本题场景下，只需要维护k个有序的序列，所以使用优先级队列是最优的。
此时就需要考虑是使用小顶堆还是大顶堆了。
如果使用大顶堆，定义一个大小为k的大顶堆，在每次更新大顶堆的时候都把最大的元素弹出去，无法保留前k个高频元素，也可以用大顶堆把所有的元素都排序了（效率相对来说不高）。
使用小顶堆，统计最大的前k个元素，所以只有小顶堆可以每次将最小的元素弹出，最后小顶堆中剩下的就是前k个最大元素。
如下图例子的图解：

《代码随想录》一刷记录_第8张图片
代码如下：

class Solution
{
	public:
		//小顶堆
		class mycomparison
		{
			public:
				bool operator()(const pair<int,int> &lhs,const pair<int,int> &rhs)
				{
					return lhs.second>rhs.second;
				}
		};	
		vector<int> topKFrequent(vector<int> &nums,int k)
		{
			//统计元素出现的次数
			unordered_map<int,int> map; //map
			for(int i=0;i<nums.size();i++)
			{
				map[nums[i]]++;
			}
			//对元素出现的次数进行排序
			//定义一个小顶堆，大小为k
			priority_queue<pair<int,int>,vector<pair<int ,int>>,mycomparison> pri_que;
			
			//用固定大小为k的小顶堆遍历所有元素出现次数的数值
			for(unordered_map<int,int>::iterator it=map.begin();it!=map.end();it++)
			{
				pri_que.push(*it);
				//如果堆的大小大于k，则对列弹出，保证堆的大小一直为k
				if(pri_que.size()>k)
					pri_que.pop();
			}
			//找出前k个高频元素，因为小顶堆先弹出的是最小的元素，所以倒序输出到result数组中
			vector<int> result(k);
			for(int i=k-1;i>=0;i--)
			{
				result[i]=pri_que.top().first;
				pri_que.pop();
			}
			return result;
		}
		
};

接雨水

题目描述：
给出一排宽度为1、高度为n的柱子，求可以接到雨水的面积（力扣42）

举个例子便于理解题干：
实例：
输入： height=[1,0,2,1,3,1,0,1,2,0,1] 输出： 7
如下图：
浅色部分即为面积
《代码随想录》一刷记录_第9张图片

双指针解法

计算面积，有两种方向，一种是按照行，一种是按照列。
本题思路按照列计算雨水的面积
由题意知道，宽度都是1，则求每一列雨水的高度（有点类似那个木桶装水，装的多少取决于最低的那个板子）。
如下图：
《代码随想录》一刷记录_第10张图片
求列5的雨水高度为列4和列8的高度的最小值减去列5的高度，即min（lHeight,rHeight）-height。由此可知每一列雨水的高度取决于该列左侧最高的柱子和右侧最高的柱子之间的最矮柱子的高度。
并且注意，第一个柱子和最后一个柱子不接雨水。
代码如下：

class Solution
{
	public:
		int trap(vector<int> &height)
		{
			int area=0;//面积
			for(int i=0;i<height.size();i++)
			{
				//第一根柱子和最后一根柱子不接水
				if(i==0 || i==(height.size()-1))
					continue;
				int rHeight=height[i];//该柱子右边最高柱子
				int lHeight=height[i];//该柱子左边最高柱子
				//找这根柱子右边的最高的柱子
				for(int r=i+1;r<height.size();r++)
				{
					if(rHeight<height[r])
						rHeight=height[r];
				}
				//找这根柱子左边的最高的柱子
				for(int l=i-1;l>=0;l--)
				{
					if(lHeight<height[l])
						lHeight=height[l];
				}
				int high=min(lHeight,rHeight)-height[i];
				if(high>0)
					area+=(high*1);//宽度题目给了为1
			}
			return area;
		}
};

时间复杂度O（n^2）相对较高
空间复杂度O（1）

动态规划解法

通过上面的双指针，我们知道为了得到两边的最高高度，使用了双指针来遍历，每到一个柱子都向两边遍历一遍，这其实是有重复计算的。
我们将每个位置的左边最高高度记录在一个数组中(maxLeft),将右边最高高度记录在另一个数组中(maxRight)，避免了重复计算，这时就用到了动态规划

当前位置的左边最高高度是前一个位置的左边最高高度和本高度比较后的一个值。
（1）从左向右遍历：maxLeft[i]=max(height[i],maxLeft[i-1])
（2）从右向左遍历：maxRight[i]=max(height[i],maxRight[i+1])

代码如下：

class Solution
{
	public:
		int trap(vector<int> &height)
		{
			//柱子数大于等于3才可能接水
			if(height.size()<=2)
				return 0;
			vector<int> maxLeft(height.size(),0);
			vector<int> maxRight(height.size(),0);
			int size=maxRight.size();
			
			//记录每个柱子左边柱子的最大高度
			maxLeft[0]=height[0];
			for(int i=1;i<size;i++)
			{
				maxLeft[i]=max(height[i],maxLeft[i-1]);
			}
			
			//记录每个柱子右边柱子的最大高度
			maxRight[size-1]=height[size-1];
			for(int i=size-2;i>=0;i--)
			{
				maxRight[i]=max(height[i],maxRight[i+1]);
			}
			
			//求面积的和
			int area=0;
			for(int i=0;i<size;i++)
			{
				int high=min(maxLeft[i],maxRight[i])-height[i];
				if(high>0)
					area+=(high*1);
			}
			return area;
		}		
};

单调栈解法

单调栈就是保持栈内元素有序

八、二叉树

二叉树种类

满二叉树：二叉树的深度为k（从1开始计算），有2^k-1个节点。

完全二叉树：除了底层节点可能没填满，其余每层的节点数都达到最大值，并且底层的节点都集中在该层最左边的若干位置。

二叉搜索树：是一个有序树，满足如下规则：若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值；若它的右子树不空，则右子树上所有节点的值均大于它的根节点的值。它的左、右子树也分别为二叉排序树。

平衡二叉搜索树（AVL树）：它是一棵空树，或者它的左右两个子树的高度差的绝对值不超过1，并且左右两个子树都是一棵平衡二叉树。

二叉树的遍历方式

（1）深度优先遍历：先往深处遍历，遇到叶子节点时再往回遍历
前中后序遍历（递归法、迭代法）
（2）广度优先遍历：一层一层地遍历
层次遍历（迭代法）

二叉树定义

代码如下：

struct TreeNode
{
	int val;
	TreeNode *left;
	TreeNode *right;
	TreeNode(int val): val(val),left(nullptr),right(nullptr) {}
};

前、中、后序的递归遍历

确定递归算法的三个要素：（1）确定递归函数的参数和返回值 （2）确定终止条件 （3）确定单层递归的逻辑。
遍历的代码如下：

class Solution
{
	public:
		//前序遍历
		void tarversal(TreeNode *cur,vector<int> &vec)
		{
			//终止条件
			if(cur==NULL)
				return;
			vec.push_back(cur->val);//中
			traversal(cur->left,vec);//左
			traversal(cur->right,vec);//右
		}
		//中序遍历
		void traversal(TreeNode *cur,vector<int> &vec)
		{
			if(cur==NULL)
				return;
			traversal(cur->left,vec);//左
			vec.push_back(cur->val);//中
			traversal(cur->right,vec);//右
		}		
		//后序遍历
		void traversal(TreeNode *cur,vector<int> &vec)
		{
			if(cur==NULL)
				return;
			traversal(cur->left,vec);//左
			traversal(cur->right,vec);//右
			vec.push_back(cur->val);
		}
		
		vector<int> preorderTraversal(TreeNode *root)
		{
			vector<int> result;
			traversal(root,result);
			return result;
		}
};

前、中、后序的迭代遍历

二叉树的前序遍历

题目描述：
二叉树的前序遍历（力扣144）
思路：
如上实现了递归遍历，递归其实就类似于栈处理。
前序遍历的顺序是中---->左----->右，，因此每次处理中间节点，先将根节点加入栈，然后将右孩子加入栈，最后将左孩子加入栈。这样才能保证出栈的顺序是中---->左----->右

前序遍历代码如下：

class Solution
{
	public:
		vector<int> preorderTraversal(TreeNode *root)
		{
			stack<TreeNode*>st;
			vector<int> result;
			if(root==NULL)
				return result;
			st.push(root);
			while(!st.empty())
			{
				TreeNode *node=st.top();
				st.pop();
				result.push_back(node->val);
				if(node->right) //空节点不入栈
					st.push(node->right);
				if(node->left)
					st.push(node->left);
			}
			return result;
		}
};
中序遍历

题目描述：
二叉树的中序遍历（力扣94）

代码如下：

class Solution
{
	public:
		vector<int> inorderTraversal(TreeNode *root)
		{
			vector<int> result;
			stack<TreeNode *>st;
			TreeNode *cur=root;
			while(cur!=NULL || !st.empty())
			{
				//指针访问节点，访问到底层
				if(cur!=NULL)
				{
					st.push(cur);//将访问的节点放入栈
					cur=cur->left;//左
				}
				else
				{
					//从栈里弹出的数据就是要处理的数据(放入result数组的数据)
					cur=st.top();
					st.pop();
					result.push_back(cur->val);//中
					cur=cur->right;//右
				}
			}
			return result;
		}
};
后序遍历

题目描述：
二叉树的后序遍历（力扣145）

思路：
后序遍历的顺序是左---->右---->中，调整前序遍历的代码顺序，变成中---->右----->左的遍历顺序，然后反转result数组，输出结果的顺序就是左----->右----->中了。
逻辑顺序如下图：
在这里插入图片描述
代码如下：

class Solution
{
	vector<int> postorderTraversal(TreeNode *root)
	{
		stack<TreeNode *>st;
		vector<int> result;
		if(root==NULL)
			return result;
		st.push(root);
		while(!st.empty())
		{
			TreeNode *node=st.top();
			st.pop();
			result.push_back(node->val);
			//相对于前序遍历，这里更改一入栈顺序(空节点不入栈)
			if(node->left)
				st.push(node->left);
			if(node->right)
				st.push(node->right);
		}
		//将结果反转之后就是左--->右---->中的顺序了
		reverse(result.begin(),result.end());
		return result;
	}
};

前、中、后序统一迭代法

1.使用迭代法实现中序遍历
代码如下：

class Solution
{
	public:
		vector<int> inorderTraversal(TreeNode *root)
		{
			vector<int> result;
			if(root!=NULL)
				st.push(root);
			while(!st.empty())
			{
				TreeNode *node=st.top();
				if(node!=NULL)
				{
					//将该节点弹出，避免重复操作，下面再将右、中、左节点添加到栈中
					st.pop();
					//添加右节点（空节点不入栈）
					if(node->right)
						st.push(node->right);
					st.push(node);//添加中节点
					st.push(NULL);//中节点访问过，但还没有处理，加入空节点作为标记
					//添加左节点（空节点不入栈）
					if(node->left)
						st.push(node->left);
					else
					{ //只有遇到空节点的时候，才将下一个节点放入结果集
					    st.pop();//将空节点弹出;
					    node=st.top();//重新取出栈中的元素
					    st.pop();
					    result.push_back(node->val);//加入结果集
					}				
				}
			}
			return result;
		}	
};

2.使用迭代法实现前序遍历
代码如下：

class Solution
{
	public:
		vector<int> preorderTraversal(TreeNode *root)
		{
			vector<int> result;
			stack<TreeNode *> st;
			if(root !=NULL)
				st.push(root)
			while(!st.empty())
			{
				TreeNode *node=st.top();
				st.pop();
				if(node!=NULL)
				{
					if(node->right)
						st.push(node->right);
					if(node-left)
						st.push(node->left);
					st.push(node);
					st.push(NULL);
				}
				else
				{
					node=st.top();
					st.pop();
					result.push_back(node->val);
				}
			}
			return result;
		}
};

3.使用迭代法实现后序遍历
代码如下：

class Solution
{
	vector<int> postorderTraversal(TreeNode *root)
	{
		vector<int> result;
		stack<TreeNode *>st;
		if(root !=NULL)
			st.push(root);
		while(!st.empty())
		{
			TreeNode *node=st.top();
			st.pop();
			if(node!=NULL)
			{
				st.push(node);
				st.push(NULL);
				if(node->right)
					st,push(node->right);
				if(node->left)
					st.right(node->left);
			}
			else
			{
				node=st.top();
				st.pop();
				result.push_back(node->val);
			}
		}		
		return result;
	}
};

二叉树的层序遍历

题目描述：
二叉树的层序遍历(力扣102)

思路：
层序遍历需要借用一个辅助数据结构即队列实现，队列先进先出。符合一层一层遍历的逻辑，而使用栈先进后出适合模拟深度优先遍历，也就是递归的逻辑。

代码如下：

class Solution
{
	public:
		vector<vector<int>> levelOrder(TreeNode *root)
		{
			queue<TreeNode*> que;
			if(root!=NULL)
				que.push(root);
			vector<vector<int>> result;
			while(!que.empty())
			{
				int size=que.size();
				vector<int> vec;
				//这里一定要使用固定大小size,不要使用que.size(),因为size是不断变化的
				for(int i=0;i<size;i++)
				{
					TreeNode *node=que.front();
					que.pop();
					vec.push_back(node->val);
					if(node->left)
						que.push(node->left);
					if(node->right)
						que.push(node->right);
				}
				result.push_back(vec);
			}
			return result;
		}
};

反转二叉树

题目描述：
反转一棵二叉树（力扣226）
如下图所示：
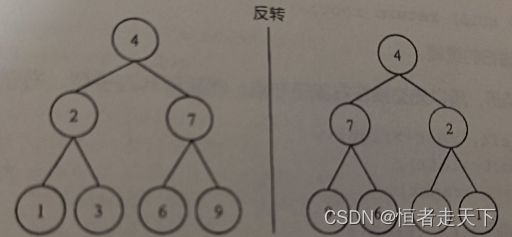
《代码随想录》一刷记录_第11张图片
思路：
想反转二叉树，就是把每个节点的左右孩子交换一下即可
关键在于遍历顺序，应该选哪一种遍历顺序呢？
遍历的过程中反转每个节点的左右孩子就可以达到整体反转的效果，只要把每一个节点的左右孩子反转一下，就可以达到整体反转的效果
这道题目使用前序遍历和后序遍历都可以，唯独中序遍历不方便，因为中序遍历会把某些节点的左右孩子反转两次。

递归法

采用前序遍历
代码如下：

class Solution
{
	public:
		TreeNode* invertTree(TreeNode *root)
		{
			if(root==NULL)
				return root;
			swap(root->left,root->right);//中
			invertTree(root->left);//左
			invertTree(root->right);//右
			return root;
		}
};
迭代法

前序遍历代码如下：

class Solution
{
	public:
		TreeNode* inverTree(TreeNode* root)
		{
			if(root==NULL)
				return root;
			stack<TreeNode*> st;
			st.push(root);
			while(!st.empty())
			{
				TreeNode *node=st.top();//中
				st.pop();
				swap(node->left,node->right);
				if(node->right)
					st.push(node->right);
				if(node->left)
					st.push(node->left);
			}
			return root;
		}
};

层序遍历代码如下：

class Solution
{
	public:
		TreeNode* invertTree(TreeNode* root)
		{
			queue<TreeNode*> que;
			if(root!=NULL)
				que.push(root);
			while(!que.empty())
			{
				int size=que.size();
				for(int i=0;i<size;i++)
				{
					TreeNode* node=que.front();
					que.pop();
					swap(node->left,node->right);
					if(node->left)
						que.push(node->left);
					if(node->right)
						que.push(node->right);
				}
			}
			return root;
		}
};

对称二叉树

题目描述：
给出一个二叉树，判断其是不是中心轴对称的（力扣101）
如下图实例：
《代码随想录》一刷记录_第12张图片

思路：
判断二叉树是否对称，，要比较的可不是左右节点，要比较的是根节点的左子树与右子树是不是相互反转的，
本题只能是“后序遍历”，因为这是要判断根节点的左右子树对应的节点互相是否相等。因此，准确的说，一棵树的遍历顺序是左---->右----->中，另一棵树的遍历顺序是右—>左----->中。两个遍历顺序都可以理解为后序遍历。

递归法

确定递归三要素：
（1）确定递归函数的参数和返回值
要比较根节点的两棵子树是否相互反转，进而判断这棵树是不是对称树，所以要比较的是两棵树，参数是左子树节点和右子树节点，返回值是bool类型。
代码如下：

bool compare(TreeNode *left,TreeNode *right)

（2）确定终止条件。
要比较两个节点的数值是否相同，首先要确定两个节点是否为空，否则后面比较数值的时候就会操作空指针。
节点为空情况：
左节点为空，右节点不为空，不对称，返回false
左节点不为空，右节点为空，不对称，返回false
左右节点都为空，对称，返回true；
对于节点不为空，比较节点数值，不相同就返回false
代码如下：

if(left==NULL && right !=NULL)
	return false;
else if(left !=NULL && right==NULL)
	return false;
else if(left->val !=right->val)
	return false;

（3）确定单层递归的逻辑
单层递归的逻辑就是处理左右节点都不为空且数值相同的情况。
比较左节点的左孩子和右节点的右孩子；比较左节点的右孩子和右节点的左孩子。
代码如下：

bool outside=compare(left->left,right->right);
bool inside=compare(left->right,right->left);
bool isSame=outside && inside;
return isSame;

上面这代码用的遍历方式是左---->右----->中和右----->左----->中

完整代码如下：

class Solution
{
	public:
		bool compare(TreeNode *left,TreeNode *right)
		{
			//首先排除空节点的情况
			if(left==NULL && right !=NULL)
				return false;
			else if(left !=NULL && right==NULL)
				return false;
			else if(left==NULL && right==NULL)
				return true;
			//排除了空节点，再排除数值不相同的情况
			else if(left->val !=right->val)
				return false;
			//此时就是左右节点都不为空且数值相同的情况
			//此时才做递归，做下一层的判断
			//左子树：左，右子树：右
			bool outside=compare(left->left,right->right);
			//左子树：右，右子树：左
			bool inside=compare(left->right,right->left);
			//左子树：中，右子树：
			bool isSname=outside && inside;
			return isSname;
		}		
		bool isSymmetric(TreeNode *root)
		{
			if(root==NULL)
				return true;
			return compare(root->left,root->right);
		}
};
迭代法

此题本质就是判断两棵树是否相互反转。
（1）使用队列
通过队列判断根节点的左右子树是否相等，分别有两个指针指向根节点的左右子树。将队列元素弹出并比较是否相等，如果两个指针指向的元素相等，继续把两个元素的左右孩子添加到队列中。继续从队列中取出两个元素并比较是否相同，如果最后队列为空依然没有找到两个不相同的元素，那么这棵树就是对称二叉树。

代码如下：

class Solution
{
	public:
		bool isSymmetric(TreeNode *root)
		{
			if(root==NULL)
				return true;
			queue<TreeNode *> que;
			que.push(root->left);//将左子树头节点加入队列
			que.push(root->right);//将右子树头节点加入队列
			while(!que.empty())
			{  //接下来判断这两棵树是否相互反转
				TreeNode  *leftNode=que.front(); que.pop();
				TreeNode  *rightNode=que.front(); que.pop();
				//左节点为空、右节点为空，说明是对称的
				if(!leftNode && !rightNode)
				{
					continue;
				}
				//左右一个节点不为空，或者都不为空但数值不相同，返回false
				if(!leftNode || !rightNode || (leftNode->val !=rightNode->val))
				{
					return false;
				}
				que.push(leftNode->left); //加入左节点的左孩子
				que.push(rightNode->right);//加右节点的右孩子
				que.push(leftNode->right); //加入左节点的右孩子
				que.push(rightNode->left); //加入右节点的左孩子
			}
		}	
};

（2）使用栈
迭代法就是把左右两棵子树要比较的元素按照一定顺序放进一个容器，然后成对地取出来进行比较，那么使用栈也是可以的。
代码如下：

class Solution
{
	public:
		bool isSymmetric(TreeNode *root)
		{
			if(root==NULL)
				return true;
			stack<TreeNode *> st;//这里改成了栈
			st.push(root->left);
			st.push(root->right);
			while(!st.empty())
			{
				TreeNode *leftNode=st.top();st.pop();
				TreeNode *leftNode=st.top();st.pop();
				if(!leftNode && !rightNode)
					continue;
				if(!leftNode || !rightNode || (leftNode->val !=rightNode->val))
					return false;
				st.push(leftNode->left);
				st.push(rightNode->right);
				st.push(leftNode->right);
				st.push(rightNode->left);
			}
			return true;
		}
};

二叉树的最大深度

题目描述：
求一棵二叉树的最大深度，根节点的深度为1。（力扣104）

递归法

代码如下：

class Solution
{public:
	int  getDepth(TreeNode *node)
	{
		if(node==NULL)
			return 0;
		int leftDepth=getDepth(node->left);
		int rightDepth=getDepth(node->right);
		int depth=1+max(leftDepth,rightDepth);
		return depth;
	}
	int maxDepth(TreeNode *root)
	{
		return getDepth(root);
	}
};

精简代码如下：

class Solution
{
	public:
		int maxDepth(TreeNode *root)
		{
			if(root==NULL)
				return 0;
			return 1+max(maxDepth(root->left),maxDepth(root->right));
		}
};

迭代法

代码如下：

class Solution
{
	public:
		int maxDepth(TreeNode *root)
		{
			if(root==NULL)
				return 0;
			int depth=0;
			queue<TreeNode *> que;
			que.push(root);
			while(!que.empty())
			{
				int size=que.size();
				depth++;//记录深度
				for(int i=0;i<size;i++)
				{
					TreeNode *node=que.front();
					que.pop();
					if(node->left)
						que.push(node->left);
					if(node->right)
						que.push(node->right);
				}
			}
			return depth;
		}
};

二叉树的最小深度

题目描述：
二叉树的最小深度（力扣111）
最小深度：从根节点到最近叶子节点的最短路径上的节点数量。

思路：
注意：最小深度是从根节点到最近叶子结点的最短路径上的节点数量。左右孩子都为空的节点才是叶子节点。
《代码随想录》一刷记录_第13张图片
注意上图情况

递归法

代码如下：

class Solution
{
	public:
		int getDepth(TreeNode *node)
		{
			if(node==NULL)
				return 0;
			int leftDepth=getDepth(node->left);//左
			int rightDepth=getDepth(node->right);//右
			//中
			//当左子树为空，右不为空时，并不是最小深度
			if(node->left==NULL && node->right !=NULL)
				return 1+rightDepth;
			//当右子树为空、左子树不为空时，并不是最小深度
			if(node->left !=NULL && node->right==NULL)
				return 1+leftDepth;
			int result=1+min(leftDepth,rightDepth);
			return result;
		}
		int minDepth(TreeNode *root)
		{
			return getDepth(root);
		}
};

迭代法

注意的是，只有当左右孩子都为空的时候，才说明遍历到最低点了，如果其中一个孩子为空则不是最低点。
代码如下：

class Solution
{
	public:
		int minDepth(TreeNode *root)
		{
			if(root==NULL)
				return 0;
			int depth=0;
			queue<TreeNode *>que;
			que.push(root);
			while(!que.empty())
			{
				int size=que.size();
				depth++;
				for(int i=0;i<size;i++)
				{
					TreeNode *node=que.front();
					que.pop();
					if(node->left)
						que.push(node->left);
					if(node->right)
						que.push(node->right);
					if(!node->left && !node->right)
						//当左右孩子都为空的时候，说明是二叉树的底层了，退出
						return depth;
				}
			}
			return depth;
		}
};

平衡二叉树

题目描述：
平衡二叉树：每一个节点的左子树和右子树的高度差的绝对值不超过1。（力扣110）

思路：
二叉树节点的深度：从根节点到该节点的最长简单路径边的条数。（或者节点数）
二叉树节点的高度：从该节点到叶子节点的最长简单路径边的条数。（或者节点数）
求高度和求深度所用的遍历方式是不一样的，求深度要从上到下去查找，所以需要前序遍历（中—>左—>右），而高度只能从下到上去查找，所以需要后序遍历（左—>右—>中）。

递归法

代码如下：

class Solution
{
	public:
		//返回以该节点为根节点的二叉树的高度，如果不是二叉搜索树则返回-1
		int getDepth(TreeNode *node)
		{
			if(node==NULL)
				return 0;
			int leftDepth=getDepth(node->left);
			if(leftDepth==-1) //说明左子树已经不是二叉平衡树
				return -1;
			
			int rightDepth=getDepth(node->right);
			if(rightDepth==-1)//说明右子树已经不是二叉平衡树
				return -1;
			
			int result;
			if(abs(leftDepth-rightDepth)>1)  //中
				result=-1;
			else
				//以当前节点为根节点的最大高度
				result=1+max(leftDepth,rightDepth);
			return result;
			/*精简代码如下：
			return abs(leftDepth-rightDepth)>1 ? -1: 1+max(leftDepth,rightDepth); */
		}
		bool isBalanced(TreeNode *root)
		{
			return getDepth(root)==-1 ? false : true;
		}
};
迭代法

通过栈模拟的后序遍历查找每个节点的高度（通过求以传入节点为根节点的二叉树的最大深度来求高度）

二叉树的所有路径

题目描述：
给出一个二叉树，返回所有从根节点到叶子节点的路径。（力扣257）

实例如下：
《代码随想录》一刷记录_第14张图片
思路：
这道题是求从根节点到叶子节点的所有路径，所以需要使用前序遍历，才方便让父节点指向子节点，找到对应的路径。

递归法

依旧依照三部曲
（1）确定递归函数参数和返回值
传入二叉树根节点的同时还要用两个数组分别记录每一条路径path和最终结果集result，这里不需要返回值，代码如下：

void traversal(TreeNode *cur,vector<int> &path,vector<string> &result)

(2)确定递归终止条件
找到叶子节点为止，代码如下：

if(cur->left==NULL && cur->right==NULL)
{
	终止处理逻辑
}

这里使用vector path记录路径，所以要把vector转为字符串，再把这个字符串放入到result数组中。
终止处理逻辑代码如下：

if(cur->left==NULL && cur->right==NULL)
{	//遇到叶子节点
	string spath;
	//将path中记录的路径转为string格式
	for(int i=0;i<path.size()-1;i++)
	{
		spath+=to_string(path[i]);
		spath+="->";
	}
	spath+=to_string(path[path.size()-1]);//记录最后一个节点（叶子节点）
	result.push_back(spath);//收集一个路径
	return;
}

(3)确定单层递归逻辑
因为是前序遍历，所以需要先处理中间节点，中间节点就是我们要记录的路径上的节点，先放进path中，即path.push_back(cur->val),然后就是递归和回溯的过程。（回溯和递归要永远写在一起）
代码如下：

if(cur->left)
{
	traversal(cur->left,path,result);
	path.pop_back();//回溯
}
if(cur->right)
{
	traversal(cur->right,path,result);
	path.pop_back();//回溯
}

整体代码如下：

class Solution
{
	private:
		void traversal(TreeNode *cur,vector<int> &path,vector<string> &result)
		{
			path.push_back(cur->val);
			//这才到了叶子节点
			if(cur->left==NULL && cur->right==NULL)
			{
				string spath;
				for(int i=0;i<path.size()-1;i++)
				{
					spath+=to_string(path[i]);
					spath+="->";
				}
				spath+=to_string(path[path.size()-1]);
				result.push_back(spath);
				return ;
			}
			if(cur->left)
			{
				traversal(cur->left,path,result);
				path.pop_back();//回溯
			}
			if(cur->right)
			{
				traversal(cur->right,path,result);
				path.pop_back();//回溯
			}
		}
	public:
		vector<string> binaryTreePaths(TreeNode *root)
		{
			vector<string> result;
			vector<int> path;
			if(root==NULL)
				return result;
			traversal(root,path,result);
			return result;
		}
};

迭代法

模拟递归过程除了需要一个栈，还需要另一个栈来存放对应的遍历路径。
代码如下：

class Solution
{
	public:
		vector<string> binaryTreePaths(TreeNode *root)
		{
			stack<TreeNode*> treeSt;//保存树的遍历节点
			stack<string> pathSt;//保存遍历路径的节点
			vector<string> result; //保存最终路径集合
			if(root==NULL)
				return result;
			treeSt.push(root);
			pathSt.push(to_string(root->val));
			while(!treeSt.empty())
			{
				TreeNode *node=treeSt.top();
				treeSt.pop();//取出节点，中
				string path=pathSt.top();
				pathSt.pop();//取出该节点对应的路径
				if(node->left==NULL && node->right==NULL)
				{ //遇到叶子节点
					result.push_back(path);
				}
				if(node->right)
				{//右
					treeSt.push(node->right);
					pathSt.push(path+"->"+to_string(node->right->val));
				}
				if(node->left)
				{//左
					treeSt.push(node->left);
					pathSt.push(path+"->"+to_string(node->left->val));
				}
			}
			return result;
		}
};

路径总和

题目描述：
找到一条从根节点到叶子节点的路径，使这个路径的节点总和等于目标值。（力扣112）

递归法

（1）确定递归函数的参数和返回值
参数：二叉树的根节点和一个计数器，这个计数器用来计算二叉树的一条边的节点之和是否正好是目标和，计数器为int类型。
代码如下：

//cur为二叉树节点，count为计数器
bool traversal(TreeNode *cur,int count);//注意函数的返回类型

（2）确定终止条件
用累减来统计计数和
递归终止条件的代码如下：

//遇到叶子节点，并且计数为0
if(!cur->left && !cur->right && count==0)  return true;
//遇到叶子节点且没有找到合适的边，直接返回
if(!cur->left && !cur->right)  return false;

（3）确定单层递归的逻辑
代码如下：

if(cur->left)
{//左（空节点不遍历）
 	//注意这里有回溯的逻辑
 	if(traversal(cur->left,count-cur->left->val))  return true;
}
if(cur->right)
{//右（空节点不遍历）
	//注意这里有回溯的逻辑
	if(traversal(cur->right,count-cur->right->val))  return true;
}
return false;

为了体现回溯过程，代码如下：

if(cur->left)//左
{
	count-=cur->left->val;//递归，处理节点
	if(traversal(cur->left,count))	return true;
	count+=cur->left->val;//回溯，撤销处理结果
}
if(cur->right)//右
{
	count-=cur->right->val;
	if(traversal(cur->right,count))  return true;
	count+=cur->right->val;
}
return false;

完整代码如下：

class Solution
{
	private:
		bool traversal(TreeNode *cur,int count)
		{
			//遇到叶子节点，并且计数为0
			if(!cur->left && !cur->right && count==0)	return true;
			if(!cur->left && !cur->right)	return false;//遇到叶子节点直接返回
			if(cur->left)
			{//左
				count-=cur->left->val;//递归，处理节点
				if(traversal(cur->left,count)) return true;
				count+=cur->left->val;
			}
			if(cur->right)
			{//右
				count-=cur->right->val;//递归，处理节点
				if(traversal(cur->right,count))  return true;
				count+=cur->right->val;//回溯，撤销处理结果
			}
			return false;
		}
	public:
		bool hasPathSum(TreeNode *root,int sum)
		{
			if(root==NULL)	return false;
			return traversal(root,sum-root->val);
		}
};
迭代法

使用栈模拟递归，此时栈内的一个元素不仅要记录该节点的指针，还要记录从头节点到该节点的路径数值的总和。用pair结构存放这个栈内的元素，将栈内的一个元素定义为pair,pair<节点指针，路径数值>

前序遍历代码如下：

class Solution
{
	public:
		bool hasPathSum(TreeNode *root,int sum)
		{
			if(root==NULL)  return false;
			//此时栈内存放的是pair<节点指针，路径数值>
			stack<pair<TreeNode*,int>> st;
			st.push(pair<TreeNode*,int>(root,root->val));
			while(!st.empty())
			{
				pair<TreeNode *,int> node=st.top();
				st.pop();
				//如果该节点是叶子节点，同时该节点的路径数值等于sum，那么就返回true
				if(!node.first->left && !node.first->right && sum==node.second)
					return true;
				
				//右节点，一个节点入栈后，记录该节点的路径数值
				if(node.first->right)
				{
					st.push(pair<TreeNode*,int>(node.first->right,node.second+node.first->right->val));
				}
				
				//左节点，一个节点入栈后，记录该节点的路径数值
				if(node.first->left)
				{
					st.push(pair<TreeNode*,int>(node.first->left,node.second+node.first->left->val));
				}
			}
			return false;
		}
};

路径总和 II

题目描述：
找到所有从根节点到叶子节点的路径，使这些路径的节点总和等于目标值。（力扣113）
思路：

代码如下：

class Solution
{
	private:
		vector<vector<int>> result;
		vector<int> path;
		//递归函数不需要返回值，因为要遍历整棵树
		void traversal(TreeNode *cur,int count)
		{//遇到叶子节点且找到了和为sum的路径
			if(!cur->left && !cur->right && count==0)
			{
				result.push_back(path);
				return;
			}
			//遇到 叶子节点且没有找到合适的边，直接返回
			if(!cur->left && !cur->right)
				return;
				
			if(cur->left)
			{ //左（空节点不遍历）
				path.push_back(cur->left->val);
				count-=cur->left->val;
				traversal(cur->left,count);//递归
				count+=cur->left->val;//回溯
				path.pop_back(); //回溯
			}	
			
			if(cur->right)
			{//右（空节点不遍历）
				path.push_back(cur->right->val);
				count-=cur->right->val;
				traversal(cur->right,count);//递归
				count+=cur->right->val;//回溯
				path.pop_back();//回溯
			}
			return ;
		}
	public:
		vector<vector<int>> pathSum(TreeNode *root,int sum)
		{
			result.clear();
			path.clear();
			if(root==NULL)	return result;
			path.push_back(root->val);//根节点放入路径
			traversal(root,sum-root->val);
			return result;
		}
	
};

构造一棵二叉树

使用中序与后序遍历序列构造二叉树

题目描述：
使用中序与后序遍历序列构造二叉树。（力扣106）
给出中序遍历和后序遍历的两个数组，通过这两个数组构造一棵二叉树。

思路：
根据两个遍历顺序构造一个唯一的二叉树的原理：以后序数组的最后一个元素作为切割点，先切割中序数组，然后根据中序数组，反过来再切割后序数组。一层一层切下去，每次后序数组的最后一个元素就是节点元素。
如下图：
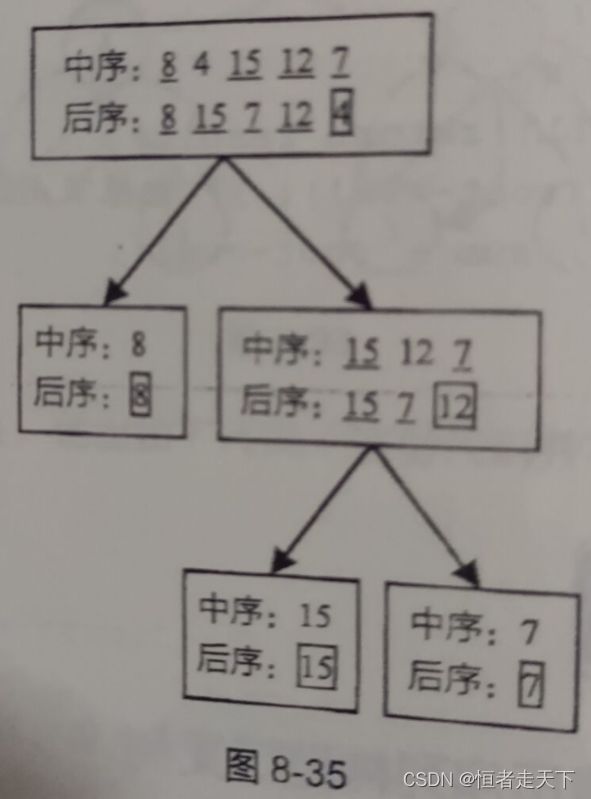
《代码随想录》一刷记录_第15张图片
分为一下几步：
（1）如果长度为0，则说明是空节点
（2）如果数组不为空，那么说明后序数组的最后一个元素是头节点元素
（3）找到后序数组的最后一个元素在中序数组中的位置并将其作为切割点
（4）切割中序数组切成中序左数组和中序又数组（一定是先切割中序数组）
（5）切割后序数组，切成后序左数组和后序右数组
（6）递归处理

代码如下：

class Solution
{
	private:
		TreeNode* traversal(vector<int> &inorder,vector<int> &postorder)
		{
			if(postorder.size()==0)
				return NULL;
			//后序数组的最后一个元素便是头节点
			int rootvalue=postorder[postorder.size()-1];
			TreeNode *root=new TreeNode(rootvalue);
			
			//叶子节点
			if(postorder.size()==1)
				return root;
			
			//找到中序遍历的切割点
			int middleindex;
			for(middleindex=0;middleindex<inorder.size();middleindex++)
			{
				if(inorder[middleindex]==rootvalue)		break;
			}
			
			//切割中序数组，采用左闭右开
			vector<int> leftinorder(inorder.begin(),inorder.begin()+middleindex);
			vector<int> rightinorder(inorder.begin()+middleindex+1,inorder.end());

			//舍弃后序数组的末尾元素
			postorder.resize(postorder.size()-1);

			//切割后序数组
			//注意后序数组的长度和中序数组的长度相同，依次为切割点
			vector<int> leftpostorder(postorder.begin(),postorder.begin()+leftinorder.size());
			vector<int> rightpostorder(postorder.begin()+leftinorder.size(),postorder.end());

			//递归处理
			root->left=traversal(leftinorder,leftpostorder);
			root->right=traversal(rightinorder,rightpostorder);
			return root;
		}
	public:
		TreeNode* buildTree(vector<int> &inorder,vector<int> &postorder)
		{
			if(inorder.size()==NULL || postorder.size()==NULL)
				return NULL;
			return traversal(inorder,postorder);
		}
};

代码优化，避免重复定义vector数组，每次用下标分割数组

class Solution
{
	private:
		//中序区间:[inorder,inorderEnd)，后序区间[postorderBegin,postorderEnd)
		TreeNode* traversal(vector<int> &inorder,int inorderBegin,int inorderEnd,vector<int> &postorder,int postorderBegin,int postorderEnd)
		{
			if(postorderBegin==postorderEnd)   return NULL;	
			
			int rootvalue=postorder[postorderEnd-1];
			TreeNode *root=new TreeNode(rootvalue);
			
			if(postorderEnd-postorderBegin==1)  return root;
			
			int delindex;
			for(delindex=inorderBegin;delindex<inorderEnd;delindex++)
			{
			   if(rootvalue==inorder[delindex])  break;	
			}
			
			//切割中序数组
			//左中序区间(左闭右开)
			int leftinorderBegin=inorderBegin;
			int leftinorderEnd=delindex;
			//右中序区间
			int rightinorderBegin=delindex+1;
			int rightinorderEnd=inorderEnd;
			
			//切割后序数组
			//左后序空间(左闭右开)
			int leftpostorderBegin=postorderBegin;
			//注意delindex-inorderBegin代表左中序数组的长度
			int leftpostorderEnd=postorderBegin+(delindex-inorderBegin);
			//右后序空间
			int rightpostorderBegin=postorderBegin+(delindex-inorderBegin);
			//舍弃最后一个元素，其已经作为节点
			int rightpostorderEnd=postorderEnd-1;
			
			//递归
			root->left=traversal(inorder,leftinorderBegin,leftinorderEnd,postorder,leftpostorderBegin,leftpostorderEnd);
			root->right=traversal(inorder,rightinorderBegin,rightinorderEnd,postorder,rightpostorderBegin,rightpostorderEnd);
			return root;
		}
	public:	
		TreeNode* buildTree(vector<int> &inorder,vector<int> &postorder)
		{
			if(inorder.size()==0 || postorder.size()==0)  return NULL;
			//左闭右开原则
			return traversal(inorder,0,inorder.size(),postorder,0,postorder.size());	
		}
};
使用前序与中序遍历序列构造二叉树

题目描述： 使用前序与中序遍历序列构造二叉树（力扣105）
思路与上题相同，代码如下：

class Solution
{
	private:
		TreeNode* traversal(vector<int> &inorder,int inorderBegin,int inorderEnd,vector<int> &preorder,int preorderBegin,int preorderEnd)
		{
			if(preorderBegin==preorderEnd)  return NULL;

			int rootvalue=preorder[preorderBegin];
			TreeNode *root=new TreeNode(rootvalue);
				
			if(preorderEnd-preorderBegin==1)	return root;

			//遍历中序数组找到头节点，来进行分割
			int delindex;
			for(int delindex=inorderBegin;delindex<inorderEnd;delindex++)
			{
				if(rootvalue==inorder[delindex])	break;
			}
			//切割中序数组
			int leftinorderBegin=inorderBegin;
			int leftinorderEnd=delindex;
			int rightinorderBegin=delindex+1;
			int rightinorderEnd=inorderEnd;

			//切割前序数组
			int leftpreorderBegin=preorderBegin+1;
			int leftpreorderEnd=leftpreorderBegin+(leftinorderEnd-leftinorderBegin);
			int rightpreorderBegin=leftpreorderEnd;
			int rightpreorderEnd=preorderEnd;

			//递归
			root->left=traversal(inorder,leftinorderBegin,leftinorderEnd,preorder,leftpreorderBegin,leftpreorderEnd);
			root->right=traversal(inorder,rightinorderBegin,rightinorderEnd,preorder,rightpreorderBegin,rightpreorderEnd);
			return root;
		}
	public:
		TreeNode* buildTree(vector<int> &preorder,vector<int> &inorder)
		{
			if(inorder.size()==0 || preorder.size()==0)	return NULL;
			//左闭右开原子
			return traversal(inorder,0,inorder.size(),preorder,0,preorder.size());
		}
};

合并两棵二叉树

题目描述：合并两棵二叉树（力扣617），如下图所示：
《代码随想录》一刷记录_第16张图片

递归法

三部曲：
（1）确定递归参数和返回值
参数两棵树的根节点，返回值是合并之后树的根节点

TreeNode* mergeTree(TreeNode *t1,TreeNode *t2)

（2）确定终止
因为传入两棵树，所以判断两棵树遍历的节点t1和t2，如果t1为NULL，那么两个节点合并后就是t2（如果t2也为NULL，那么合并之后就是NULL）。
如果t2为NULL，那么两棵树合并后就是t1（如果t1也为NULL，那么合并之后就是NULL）。
代码如下：

if(t1==NULL) return t2;//如果t1为空，那么这两棵树合并之后就应该是t2
if(t2==NULL) return t1;//如果t2为空，那么这两棵树合并之后就应该是t1

（3）确定单层递归的逻辑
可以重复利用t1这棵树，t1就是合并之后树的根节点（修改了原来树的结构）。在单层递归中，就要把两棵树的元素加到一起：

t1->val+=t2->val;

所以t1的左子树是合并t1左子树和t2左子树之后的左子树。t1的右子树是合并t1右子树和t2右子树之后的右子树。最终t1就是合并之后的根节点。代码如下：

t1->left=mergeTrees(t1->left,t2->left);
t1->right=mergeTrees(t1->right,t2->right);
return t1;

完整代码（修改t1数值结构）：

class Solution
{
	public:
		TreeNode* mergeTrees(TreeNode *t1,TreeNode *t2)
		{
			if(t1==NULL)	return t2;//如果t1为空，那么这两棵树合并之后就应该是t2
			if(t2==NULL)	return t1;//如果t2为空，那么这两棵树合并之后就应该是t1
			//修改t1的数值和结构
			t1->val+=t2->val;  //中
			t1->left=mergeTrees(t1->left,t2->left); //左
			t1->right=mergeTrees(t1->right,t2->right);	//右
			return t1;
		}
};

不修改输入树结构，前序遍历代码如下：

class Solution
{
	TreeNode* mergeTrees(TreeNode *t1,TreeNode *t2)
	{
		if(t1==NULL)	return t2;
		if(t2==NULL)	return t1;
		//新建合并树的节点
		TreeNode *root=new TreeNode(0);
		root->val=t1->val+t2->val;
		root->left=mergeTrees(t1->left,t2->left);
		root->right=mergeTrees(t1->right,t2->right);
		return root;
	}
};
迭代法

在迭代法中，一般使用队列同时操作两棵树模拟层序遍历

代码如下：

class Solution
{
	public:
		TreeNode* mergeTrees(TreeNode *t1,TreeNode *t2)
		{
			if(t1==NULL)	return t2;
			if(t2==NULL)	return t1;
			queue<TreeNode*> que;
			que.push(t1);
			que.push(t2);
			while(!que.empty())
			{
				TreeNode *node1=que.front();
				que.pop();
				TreeNode *node2=que.front();
				que.pop();
				
				//此时两个节点一定不为空
				node1->val+=node2->val;
				//如果两棵树的左节点都不为空，则加入队列
				if(node1->left!=NULL && node2->left!=NULL)
				{
					que.push(node1->left);
					que.push(node2->left);
				}
				//如果两棵树的右节点都不为空，则加入队列
				if(node1->right!=NULL && node2->right!=NULL)
				{
					que.push(node1->right);
					que.push(node2->right);
				}
				//当t1的左节点为空、t2的左节点不为空时，t2的左节点赋值给t1的左节点
				if(node1->left==NULL && node2->left!=NULL)
				{
					node1->left=node2->left;
				}
				//当t1的右节点为空、t2的右节点不为空时，t2的右节点赋值给t1的右节点
				if(node1->right==NULL && node2->right!=NULL)
				{
					node1->right=node2->right;
				}
			}
			return t1;
		}
};

在二叉搜索树中寻找节点

题目描述：确定一个节点是否在二叉搜索树，如果在，则返回这个节点，如果不在，则返回NULL。（力扣700）
如图是一个二叉搜索树，而且树中没有重复元素
《代码随想录》一刷记录_第17张图片

思路：
二叉树的特性如下：
（1）若它的左子树不空，则左子树上所有节点的值均小于它的根节点
（2）若它的右子树不空，则右子树上所有节点的值均大于它的根节点
（3）它的左、右子树也分别为二叉搜索树。

递归法

递归三部曲：
（1）确定递归的参数和返回值
参数：传入树的根节点，和要寻找的值
返回值：搜索值所在的节点

TreeNode* searchBST(TreeNode *root,int val)

（2）确定终止条件
如果root为空，或者找到这个数值，就返回root节点

if(root==NULL || root->val=val)	return root;

（3）单层递归逻辑
二叉搜索树节点是有序的。如果root->val大于val，则搜索左子树；如果root->val小于val，则搜索右子树。如果找不到，则返回NULL。

//这里加了return，如果要搜索一条边，那么递归函数就要加返回值
if(root->val>val)	return searchBST(root->left,val);
if(root->val<val)	return searchBST(root->right,val);
return NULL;

完整代码如下：

class Solution
{
	TreeNode* searchBST(TreeNode* root,int val)
	{
		if(root==NULL || root->val==val)	return root;
		if(root->val>val)	return searchBST(root->left,val);
		if(root->val<val)	return searchBST(root->right,val);
		return NULL;
	}
};
迭代法

对于二叉树的遍历的迭代法，使用栈模拟深度遍历，使用队列模拟广度遍历

二叉搜索树的有序性，按照查找路径直接遍历便好
代码如下：

class Solution
{
	TreeNode* searchBST(TreeNode *root,int val)
	{
		while(root!=NULL)
		{
			if(root->val>val)	root=root->left;
			else if(root->val<val)	root=root->right;
			else	return root;
		}
		return NULL;
	}
};

验证二叉搜索树

题目描述：
判断二叉树是不是二叉搜索树的条件如下（力扣98）：
（1）若它的左子树不空，则左子树上所有节点的值均小于它的根节点的值
（2）若它的右子树不为空，则右子树上所有节点的值均大于它的根节点的值
（3）它的左、右子树也分别为二叉搜索树

思路：
采用中序遍历，输出的二叉搜索树节点的数值是有序序列。验证二叉树搜索树就相当于判断一个序列是否是递增的。

递归法

代码如下：

class Solution
{
	private:
		vector<int> vec;
		void traversal(TreeNode *root)
		{
			if(root==NULL)	return ;
			traversal(root->left);
			vec.push_back(root->val);
			traversal(root->right);
		}
	public:
		bool isValidBST(TreeNode *root)
		{
			vec.clear();
			traversal(root);
			for(int i=0;i<vec.size()-1;i++)
			{
				if(vec[i]>=vec[i+1])
					return false;
			}
			return true;
		}
};
迭代法

代码如下：

class Solution
{
	public:
		bool isValidBST(TreeNode *root)
		{
			stack<TreeNode*> st;
			TreeNode *cur=root;
			TreeNode *pre=NULL;//记录前一个节点
			
			while(cur!=NULL && !st.empty())
			{
				if(cur!=NULL)
				{
					st.push(cur);
					cur=cur->left; //左
				}
				else
				{
					cur=st.top();   //中
					st.pop();
					if(pre!=NULL && cur->val<=pre->val)
					{
						   return false;
					}
					pre=cur;//保持前一个访问的节点
					cur=cur->right;
				}
			}
			return true;
		}
};

二叉搜索树的最小绝对差

题目描述：
给出一棵所有节点为非负值的二叉搜索树，请计算树中任意两个节点的差的绝对值的最小值。（力扣530）

递归法

二叉搜索树是有序的。遇到在二叉搜索树上求最值、求差值等问题，就把它想成在一个有序数组上求最值、求差值。
代码如下：

class Solution
{
	private:
		vector<int> vec;
		void traversal(TreeNode *root)
		{
			if(root==NULL)	return;
			traversal(root->left);
			vec.push_back(root->val); //将二叉搜索树转换为有序数组
			traversal(root->right);
		}
	public:
		 int getMinimumDifference(TreeNode *root)
		 {
		 	vec.clear();
		 	traversal(root);
		 	if(vec.size()<2)	return 0;
		 	int result=INT_MAX;
		 	//统计有序数组的最小差值
		 	for(int i=1;i<vec.size();i++)
		 	{
		 		result=min(result,vec[i]-vec[i-1]);
		 	}
		 	return result;
		 }
};

在遍历过程中，直接找到相邻两个节点的差值-----用一个pre节点记录cur节点的前一个节点。
如图所示：
《代码随想录》一刷记录_第18张图片
代码如下：

class Solution
{
	private:
		int result=INT_MAX;
		TreeNode *pre;
		void traversal(TreeNode *cur)
		{
			if(cur==NULL)	return;
			traversal(cur->left); //左
			if(pre!=NULL)   //中
				result=min(result,cur->val-pre->val);
			pre=cur; //记录前一个节点的指针
			traversal(cur->right);
		}
	public:
		int getMinimumDifference(TreeNode *root)
		{
			traversal(root);
			return result;
		}
};
迭代法

中序遍历迭代法，代码如下：

class Solution
{
	public:
		int getMinmumDifference(TreeNode *root)
		{
			stack<TreeNode *>st;
			TreeNode *cur=root;
			TreeNode *pre=NULL;
			int result=INT_MAX;
			while(cur !=NULL || !st.empty())
			{
				if(cur!=NULL)
				{
					st.push(cur); //将访问的节点放入栈
					cur=cur->left; //左
				}
				else
				{
					cur=st.top();
					st.pop();
					if(pre!=NULL)  //中
					{
						result=min(result,cur->val-pre->val);
					}
					pre=cur;
					cur=cur->right; //右
				}
			}
			return result;
		}
};

二叉搜索树

题目描述：
二叉搜索树中的众数。（力扣501）

递归法

1.普通二叉树
遍历整棵树，用map统计元素出现的频率并排序，最后取前面高频的元素的集合，具体步骤如下：
用map统计元素出现的频率

//map,key:元素;value:元素出现的频率
void searchBST(TreeNode *cur,unordered_map<int,int> &map)
{
	//前序遍历
	if(cur==NULL)	return;
	map[cur->val]++; //统计元素频率
	searchBST(cur->left,map);
	searchBST(cur->right,map);
	return;
}

对统计的元素出现的频率（即map的value）进行排序。

bool static cmp(const pair<int,int> &a,const pair<int,int> &b)
{
	return a.second>b.second; //从大到小排序
}
vector<pair<int,int>> vec(map.begin(),map.end());
sort(vec.begin(),vec.end(),cmp); //将频率排序

取前面高频出现的元素，此时数组vector中存放的是排序后的pair，把前面高频出现的元素取出来即可。
代码如下：

result.push_back(vec[0].first);
for(int i=1;i<vec.size();i++)
{
	//取出现频率最高的元素放入result数组
	if(vec[i].second==vec[0].second)
		result.push_back(vec[i].first);
	else
		break;
}
return result;

整体代码如下：

class Solution
{
	private:
		void searchBST(TreeNode *cur,unordered_map<int,int> &map)
		{
			if(cur==NULL)	return ;
			map[cur->val]++;
			searchBST(cur->left,map);
			searchBST(cur->right,map);
			return;
		}
		bool static cmp(const pair<int,int> &a,const pair<int,int> &b)
		{
			return a.second>b.second;
		}
	public:
		vector<int> findMode(TreeNode *root)
		{
			unordered_map<int,int> map;
			vector<int> result;
			if(root==NULL)	return result;
			searchBST(root,map);
			vector<pair<int,int> vec(map.begin(),map.end());
			sort(vect.begin(),vec.end(),cmp);
			result.push_back(vec[0].first);
			for(int i=1;i<vec.size();i++)
			{
				if(vec[0].second==vec[i].second)
					result.push_back(vec[i].first);
				else
					break;
			}
			return result;
		}
};

2.二叉搜索树
如图所示，对二叉搜索树进行中序遍历后的输出为[1,3,3,5,8,8]。
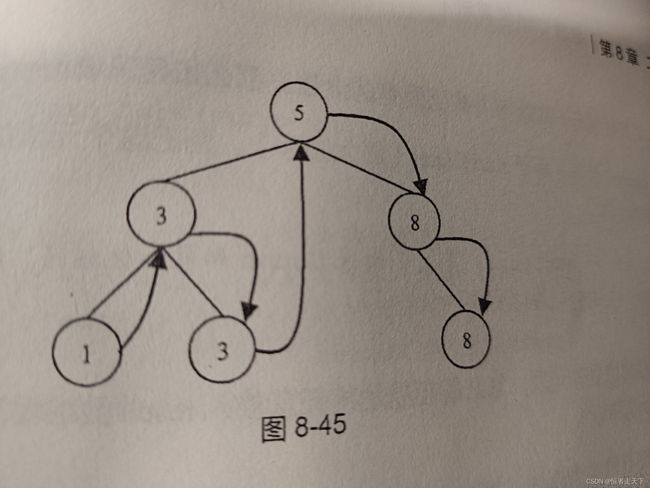
《代码随想录》一刷记录_第19张图片
中序遍历代码：

void searchBST(TreeNode *cur)
{
	if(cur==NULL)	return;
	searchBST(cur->left); //左
	(处理节点)
	searchBST(cur->right); //右
	return ;
}

相邻的两个元素作比较，然后输出出现频率最高的元素。
代码如下：

if(pre==NULL)
{
	//第一个节点，频率为1
	count=1;
}
else if(pre->val==cur->val)
{
	//与前一个节点的数值相同
	count++；
}
else
{
	//与前一个节点的数值不同
	count=1;
}
pre=cur; //更新上一个节点

如果count（频率）等于maxCount（最大频率），则把这个元素加入结果集
代码如下：

if(count==maxCount)
{
 //如果count和最大值相同，则将其放入result
 result.push_back(cur->val);
}

完整代码如下：

class Solution
{
	private:
		int maxCount; //最大频率
		int count; //统计频率
		TreeNode *pre;
		vector<int> result;
		void searchBST(TreeNode* cur)
		{
			if(cur==NULL)	return;
			searchBST(cur->left); //左
			//中
			if(pre==NULL)
				//第一个节点
				count=1;
			else if(pre->val==cur->val)
				//与前一个节点的数值相同
				count++;
			else
				//与前一个节点的数值不同
				count=1;
			pre=cur;//更新上一个节点
			
			if(count==maxCount)
				//如果和最大值相同，则将其放入result
				result.push_back(cur->val);
			
			//如果计数大于最大频率
			if(count>maxCount)
			{
				maxCount=count;//更新最大频率
				result.clear();//之前result中的元素都失效了
				result.push_back(cur->val);
			}	
			searchBST(cur->right);//右
			return ;
		}
	public:
		vector<int> findMode(TreeNode *root)
		{
			
			maxCount=0;//最大频率
		    count=0;//统计频率
			TreeNode *pre=NULL;
			result.clear();
			searchBST(root);
			return result;
		}
};
迭代法

把中序遍历转成迭代法即可
代码如下：

class Solution
{
	public:
		vector<int> findMode(TreeNode *root)
		{
			stack<TreeNode*> st;
			TreeNode* cur=root;
			TreeNode* pre=NULL;
			int maxCount=0; //最大频率
			int count=0;//统计频率
			vector<int> result;
			while(cur!=NULL || !st.empty())
			{
				if(cur!=NULL)
				{
					st.push(cur); //将访问的节点放入栈
					cur=cur->left;//左
				}
				else
				{
					//中
					cur=st.top();
					st.pop();
					if(pre==NULL)	
						count=1;
					else if(pre->val==cur->val)
						count++;
					else
						count=1;
					
					if(count==maxCount)
						result.push_back(cur->val);
						
					if(count>maxCount)
					{
						maxCount=count;
						result.clear();
						result.push_back(cur->val);
					}
					pre=cur;
					cur=cur->right; //右
				}
			}
			return result;
		}
};

二叉树的最近公共祖先

题目描述：
二叉树的最近公共祖先（力扣236）

普通二叉树

思路：
如果能自底向上就好了，可以找到公共的祖先了。
二叉树如何自底向上查找呢？
二叉树回溯的过程就是自底向上，后序遍历就符合回溯的过程，最先处理的一定是叶子节点

使用后序遍历，在回溯的过程中，自底向上遍历节点，一旦发现符合这个条件的节点，那么该节点就是最近公共节点

递归三部曲：
（1）确定递归函数返回值和参数
函数要返回找到的节点q和p的最近公共节点

TreeNode *lowestCommonAncestor(TreeNode *root,TreeNode *p,TreeNode *q)

（2）确定终止条件

如果找到了节点p或q，或遇到空节点，那么就返回这个节点。

if(root==q || root==p || root==NULL)
	return NULL;

（3）单层递归逻辑
函数有返回值，这是因为回溯的过程中需要通过递归函数的返回值判断某个节点是不是公共祖先节点
搜索一条边的写法：

if(递归函数(root->left))	return;
if(递归函数(root->right)) return;

搜索整棵树

left=递归函数(root->left);
right=递归函数(root->right);
left与right逻辑处理

完整代码如下：

class Solution
{
	public:
	    /*p,q都是树上存在的节点*/
		TreeNode* lowestCommonAncestor(TreeNode *root,TreeNode *p,TreeNode *q)
		{
			if(root==q || root==p || root==NULL)
				return root;
			TreeNode *left=lowestCommonAncestor(root->left,p,q);
			TreeNode *right=lowestCommonAncestor(root->right,p,q);
			//p和q分别在根节点的左右子树上
			if(left!=NULL && right!=NULL)
				return root;
			/*子树的根节点为p或者q，并且以p或者q为该节点的子树中包括了另一个节点*/
			if(left==NULL && root!=NULL)
				return right;
			else if(left!=NULL && right==NULL)
				return left;
				
			else
			{
				return NULL;
			}
			
		}
};
二叉搜索树

题目描述：
二叉搜索树的最近公共祖先 。（力扣235）
思路：
二叉搜索树是有序的，在有序树中，判断一个节点的左子树中有p，右子树中有q：
从上到下遍历二叉搜索树，如果cur节点的数值在[p,q] 区间，则说明cur就是最近公共祖先

递归三部曲：
（1）确定递归函数返回值和参数

TreeNode* traversal(TreeNode *root,TreeNode *p,TreeNode *q)

（2）确定终止条件

（3）确定单层递归逻辑
遍历二叉搜索树的过程就是寻找区间[p->val,q->val],如果cur->val大于p->val,并且大于q->val，则向左遍历。
其他同理

整体代码如下：

class Solution
{
	private:
	    //前序遍历
		TreeNode* traversal(TreeNode *cur,TreeNode *p,TreeNode *q)
		{
			if(cur==NULL)	return cur;
			
			if(cur->val>p->val && cur->val>q->val)
			{
				TreeNode *left=traversal(cur->left,p,q);
				if(left!=NULL)
					return left;
			}
			if(cur->val<p->val && cur->val<q->val)
			{
				TreeNode *right=traversal(cur->right,p,q);
				if(right!=NULL)
					return right;
			}
			return cur;
		}
	public:
		TreeNode* lowestCommonAncestor(TreeNode *root,TreeNode *p,TreeNode *q)
		{
			return traversal(root,p,q);
		}
};

迭代法：

class Solution
{
	public:
		TreeNode* lowestCommonAncestor(TreeNode* root,TreeNode* p,TreeNode* q)
		{
			while(root)
			{
				if(root->val >p->val && root->val> q->val)
					root=root->left;
				else if(root->val < p->val && root->val < q->val)
				{
					root=root->right;
				}
				else
					return root;
			}
			return NULL;
		}
};

在二叉搜索树中插入一个节点

题目描述：
二叉搜索树中节点的数值是唯一的，新插入的节点的数值和树中节点的 数值也不同(力扣701)

思路：
只要遍历二叉搜索树，在空节点处插入即可，不用改变树的结构

递归法

（1）确定递归函数的参数和返回值
函数的参数是根节点和要插入的元素

TreeNode* insertIntoBST(TreeNode* root,int val)

(2)确定终止条件
如果当前 遍历的节点为NULL,则该节点就是要插入节点的位置，并把插入节点返回

if(root==nullptr)
{
	TreeNode *node=new TreeNode(val);
	return node;
}

（3）确定单层递归逻辑
搜索树是有方向的，可以根据插入元素的值决定递归方向

if(root->val>val) root->left=insertIntoBST(root->left,val);
if(root->val<val) root->right=insertIntoBST(root->right,val);

完整代码如下：

class Solution
{
	public:
		TreeNode* insertIntoBST(TreeNode *root,int val)
		{
			if(root==NULL)
			{
				TreeNode *node=new TreeNode(val);
				return node;
			}
			if(root->val > val)	root->left=insertIntoBST(root->left,val);
			if(root->val < val) root->right=insertIntoBST(root->right,val);
			return root;
		}
}

没有返回值的递归。代码如下：

class Solution
{
	private:
		TreeNode *parent;
		void traversal(TreeNode *cur,int val)
		{
			if(cur==NULL)
			{
				TreeNode *node=new TreeNode(val);
				if(val>parent->val)	parent->right=node;
				else	parent->left=node;
				return;
			}
			parent=cur;
			if(cur->val>val)	traversal(cur->left,val);
			if(cur->val<val)	traversal(cur->right,val);
			return;
		}
	public:
		TreeNode* insertIntoBST(TreeNode *root,int val)
		{
			parent=new TreeNode(0);
			if(root==NULL)
			{
				root=new TreeNode(val);
				return root;
			}
			traversal(root,val);
			return root;
		}
};
迭代法

迭代法遍历二叉树的过程中，记录当前遍历的节点的父节点

class Solution
{
	public:
		TreeNode* insertIntoBST(TreeNode *root,int val)
		{
			if(root==NULL)
			{
				TreeNode *node=new TreeNode(val);
				return node;
			}
			TreeNode *cur=root;
			TreeNode *parent=root;
			while(cur!=NULL)
			{
				parent=cur;
				if(cur->val > val)	cur=cur->left;
				else	cur=cur->right;
			}
			
			TreeNode *node=new TreeNode(val);
			if(val<parent->val)	parent->left=node;
			else parent->right=node;
			return root;
		}
};

在二叉搜索树中删除一个节点

题目描述：
删除二叉搜索树中的节点（力扣450）

递归法

（1）确定函数的返回值和参数

TreeNode* deleteNode(TreeNode *root,int key)

（2）确定终止条件
遇到空节点就返回，说明没有找到要删除的节点

if(root==nullptr)	return root;

（3）确定单层递归逻辑
删除节点一共有以下5种情况：
（1）没有找到删除的节点，遍历到空节点后直接返回
找到删除的节点有以下4种情况
（2）左右孩子都为空（叶子节点），直接删除节点，返回NULL
（3）被删除的节点左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
（4）被删除的节点的右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子根节点
（5）左右孩子节点都不为空，将删除节点的左子树的头节点（左孩子）放到删除节点的右子树的最左面节点的左孩子
如下图所示，删除节点5（第5种情况）


整体代码如下：

class Solution
{
	public:
		TreeNode* deleteNode(TreeNode *root,int key)
		{
			//情况一：没找到删除的节点，遍历到空节点就直接返回了
			if(root==nullptr)	return root;
			
			if(root->val==key)
			{
				//情况二：左右孩子都为空(叶子节点)，直接删除节点，返回NULL为根节点
				//情况三：其左孩子为空，右孩子不为空，删除节点，右孩子补位，返回右孩子为根节点
				if(root->left==nullptr)	return root->right;
				//情况四：其右孩子为空，左孩子不为空，删除节点，左孩子补位，返回左孩子根节点
				else if(root->right==nullptr)	return root->left;
				//情况5
				else
				{
					TreeNode *cur=root->right;//查找右子树最左面的节点
					while(cur->left !=nullptr)
					{
						cur=cur->left;
					}
					//把要删除的节点（root）的左子树放在cur的左子树的位置
					cur->left=root->left;
					TreeNode* tmp=root;//保存root节点，下面释放内存
					root=root->right;//返回旧的root的右孩子作为新root
					delete tmp;//释放节点内存
					return root;
				}
			}
			if(root->val > key)	root->left=deleteNode(root->left,key);
			if(root->val < key)	root->right=deleteNode(root->right,key);
			return root;
		}
};
迭代法

修剪二叉搜索树

题目描述：
将二叉搜索树修剪为其节点数值只在[low,high]范围内（左闭右闭区间） ）（力扣669）

递归法

（1）确定递归函数的参数和返回值
可以通过递归函数的返回值来删除节点

TreeNode* trimBST(TreeNode *root,int low,int high)

（2）确定终止条件
修剪的操作并不是在终止条件下进行的，所以遇到空节点返回即可。

if(root==nullptr)	return nullptr;

（3）确定单层递归逻辑
1.如果root（当前节点）的元素小于左边界low的数值，应该递归右子树，并返回右子树符合条件的头节点

if(root->val<low)
{
	//寻找符合[low,high]区间的节点
	TreeNode *right=trimBST(root->right,low,high);
	return right;
}

2.如果root（当前节点）的元素大于右边界high的数值，那么应该递归左子树，并返回左子树符合条件的头节点

if(root->val >high)
{
	//寻找符合[low,high]区间的节点
	TreeNode *left=trimBST(root->left,low,high);
	return left;
}

整体代码如下：

class Solution
{
	public:
		TreeNode* trimBST(TreeNode *root,int low,int high)
		{
			if(root==nullptr)	return nullptr;
			if(root->val < low)
			{
				//寻找符合[low,high]区间的节点
				TreeNode *right=trimBST(root->right,low,high);
				return right;
			}
			if(root->val > high)
			{
				TreeNode *left=trimBST(root->left,low,high);
				return left;
			}
			root->left=trimBST(root->left,low,high);
			root->right=trimBST(root->right,low,high);
			return root;
		}
};
迭代法

使用栈模拟递归的过程

class Solution
{
	public:
		TreeNode* trimBST(TreeNode *root,int low,int high)
		{
			if(!root)	return nullptr;
			//处理头节点，让root移到[low，high]范围内，注意是左闭右闭
			while(root!=nullptr && (root->val <low || root->val > high))
			{
				if(root->val < low)	root=root->right; //小于low则往右遍历
				else root=root->left;//大于high则往左遍历
			}
			TreeNode *cur=root;
			//此时root已经在[low,high]范围内，处理左孩子元素小于low的情况
			while(cur!=nullptr)
			{
				while(cur->left && cur->left->val < low)
				{
					cur->left=cur->left->right;
				}
				cur=cur->left;
			}
			cur=root;
			//此时root已经在[low,high]范围内，处理右孩子大于high的情况
			while(cur!=nullptr)
			{
				while(cur->right && cur->right->val>high)
				{
					cur->right=cur->right->left;
				}
			}
			return root;
		}
};

构造一棵平衡二叉搜索树

题目描述：
给定一个有序数组（从小到大），构造一棵二叉搜索树

递归法

（1）确定递归函数的参数和返回值

//左闭右闭区间[left,right]
TreeNode* traversal(vector<int> &nums,int left,int right)

（2）确定递归终止条件

if(left > right)  return nullptr;

（3）确定单层递归逻辑

整体代码：

class Solution
{
	private:
		TreeNode* traversal(vector<int> &nums,int left,int right)
		{
			if(left>right)	return nullptr;
			//如果数组的长度为偶数，中间位置有两个元素，则取靠左边的元素
			int mid=left+((right-left)/2);
			TreeNode *root=new TreeNode(nums[mid]);
			root->left=traversal(nums,left,mid-1);
			root->right=traversal(nums,mid+1,right);
			return root;
		}
	public:
		TreeNode* sortedArrayToBST(vector<int> &nums)
		{
			TreeNode *root=traversal(nums,0,nums.size()-1);
			return root;
		}
};

你可能感兴趣的:(算法,算法)

  • 机器学习与深度学习间关系与区别 ℒℴѵℯ心·动ꦿ໊ོ꫞ 人工智能学习深度学习python
    一、机器学习概述定义机器学习（MachineLearning,ML）是一种通过数据驱动的方法，利用统计学和计算算法来训练模型，使计算机能够从数据中学习并自动进行预测或决策。机器学习通过分析大量数据样本，识别其中的模式和规律，从而对新的数据进行判断。其核心在于通过训练过程，让模型不断优化和提升其预测准确性。主要类型1.监督学习（SupervisedLearning）监督学习是指在训练数据集中包含输入
  • Goolge earth studio 进阶4——路径修改与平滑 陟彼高冈yu Googleearthstudio进阶教程旅游
    如果我们希望在大约中途时获得更多的城市鸟瞰视角。可以将相机拖动到这里并创建一个新的关键帧。camera_target_clip_7EarthStudio会自动平滑我们的路径，所以当我们通过这个关键帧时，不是一个生硬的角度，而是一个平滑的曲线。camera_target_clip_8路径上有贝塞尔控制手柄，允许我们调整路径的形状。右键单击，我们可以选择“平滑路径”，这是默认的自动平滑算法，或者我们可
  • 基于社交网络算法优化的二维最大熵图像分割 智能算法研学社（Jack旭） 智能优化算法应用图像分割算法php开发语言
    智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码文章目录智能优化算法应用：基于社交网络优化的二维最大熵图像阈值分割-附代码1.前言2.二维最大熵阈值分割原理3.基于社交网络优化的多阈值分割4.算法结果：5.参考文献：6.Matlab代码摘要：本文介绍基于最大熵的图像分割，并且应用社交网络算法进行阈值寻优。1.前言阅读此文章前，请阅读《图像分割：直方图区域划分及信息统计介绍》htt
  • 121. 买卖股票的最佳时机 薄荷糖的味道_fb40
    给定一个数组，它的第i个元素是一支给定股票第i天的价格。如果你最多只允许完成一笔交易（即买入和卖出一支股票），设计一个算法来计算你所能获取的最大利润。注意你不能在买入股票前卖出股票。示例1:输入:[7,1,5,3,6,4]输出:5解释:在第2天（股票价格=1）的时候买入，在第5天（股票价格=6）的时候卖出，最大利润=6-1=5。注意利润不能是7-1=6,因为卖出价格需要大于买入价格。示例2:输入:
  • 每日算法&面试题，大厂特训二十八天——第二十天（树） 肥学 ⚡算法题⚡面试题每日精进java算法数据结构
    目录标题导读算法特训二十八天面试题点击直接资料领取导读肥友们为了更好的去帮助新同学适应算法和面试题，最近我们开始进行专项突击一步一步来。上一期我们完成了动态规划二十一天现在我们进行下一项对各类算法进行二十八天的一个小总结。还在等什么快来一起肥学进行二十八天挑战吧！！特别介绍小白练手专栏，适合刚入手的新人欢迎订阅编程小白进阶python有趣练手项目里面包括了像《机器人尬聊》《恶搞程序》这样的有趣文章
  • 回溯算法-重新安排行程 chirou_ 算法数据结构图论c++图搜索
    leetcode332.重新安排行程这题我还没自己ac过，只能现在凭着刚学完的热乎劲把我对题解的理解记下来。本题我认为对数据结构的考察比较多，用什么数据结构去存数据，去读取数据，都是很重要的。classSolution{private:unordered_map>targets;boolbacktracking(intticketNum,vector&result){//1.确定参数和返回值//2
  • Faiss：高效相似性搜索与聚类的利器 网络·魚 大数据faiss
    Faiss是一个针对大规模向量集合的相似性搜索库，由FacebookAIResearch开发。它提供了一系列高效的算法和数据结构，用于加速向量之间的相似性搜索，特别是在大规模数据集上。本文将介绍Faiss的原理、核心功能以及如何在实际项目中使用它。Faiss原理：近似最近邻搜索：Faiss的核心功能之一是近似最近邻搜索，它能够高效地在大规模数据集中找到与给定查询向量最相似的向量。这种搜索是近似的，
  • insert into select 主键自增_mybatis拦截器实现主键自动生成 weixin_39521651 insertintoselect主键自增mybatisdelete返回值mybatisinsert返回主键mybatisinsert返回对象mybatisplusinsert返回主键mybatisplus插入生成id
    前言前阵子和朋友聊天，他说他们项目有个需求，要实现主键自动生成，不想每次新增的时候，都手动设置主键。于是我就问他，那你们数据库表设置主键自动递增不就得了。他的回答是他们项目目前的id都是采用雪花算法来生成，因此为了项目稳定性，不会切换id的生成方式。朋友问我有没有什么实现思路，他们公司的orm框架是mybatis，我就建议他说，不然让你老大把mybatis切换成mybatis-plus。mybat
  • k均值聚类算法考试例题_k均值算法(k均值聚类算法计算题) 寻找你83497 k均值聚类算法考试例题
    ?算法：第一步：选K个初始聚类中心，z1(1),z2(1)，…，zK(1)，其中括号内的序号为寻找聚类中心的迭代运算的次序号。聚类中心的向量值可任意设定，例如可选开始的K个.k均值聚类：---------一种硬聚类算法，隶属度只有两个取值0或1，提出的基本根据是“类内误差平方和最小化”准则；模糊的c均值聚类算法：--------一种模糊聚类算法，是.K均值聚类算法是先随机选取K个对象作为初始的聚类
  • Python实现简单的机器学习算法 master_chenchengg pythonpython办公效率python开发IT
    Python实现简单的机器学习算法开篇：初探机器学习的奇妙之旅搭建环境：一切从安装开始必备工具箱第一步：安装Anaconda和JupyterNotebook小贴士：如何配置Python环境变量算法初体验：从零开始的Python机器学习线性回归：让数据说话数据准备：从哪里找数据编码实战：Python实现线性回归模型评估：如何判断模型好坏逻辑回归：从分类开始理论入门：什么是逻辑回归代码实现：使用skl
  • 推荐算法_隐语义-梯度下降 _feivirus_ 算法机器学习和数学推荐算法机器学习隐语义
    importnumpyasnp1.模型实现"""inputrate_matrix:M行N列的评分矩阵，值为P*Q.P:初始化用户特征矩阵M*K.Q:初始化物品特征矩阵K*N.latent_feature_cnt:隐特征的向量个数max_iteration:最大迭代次数alpha:步长lamda:正则化系数output分解之后的P和Q"""defLFM_grad_desc(rate_matrix,l
  • K近邻算法_分类鸢尾花数据集 _feivirus_ 算法机器学习和数学分类机器学习K近邻
    importnumpyasnpimportpandasaspdfromsklearn.datasetsimportload_irisfromsklearn.model_selectionimporttrain_test_splitfromsklearn.metricsimportaccuracy_score1.数据预处理iris=load_iris()df=pd.DataFrame(data=ir
  • 数据结构 | 栈和队列 TT-Kun 数据结构与算法数据结构栈队列C语言
    文章目录栈和队列1.栈：后进先出（LIFO）的数据结构1.1概念与结构1.2栈的实现2.队列：先进先出（FIFO）的数据结构2.1概念与结构2.2队列的实现3.栈和队列算法题3.1有效的括号3.2用队列实现栈3.3用栈实现队列3.4设计循环队列结论栈和队列在计算机科学中，栈和队列是两种基本且重要的数据结构，它们在处理数据存储和访问顺序方面有着独特的规则和应用。本文将详细介绍栈和队列的概念、结构、实
  • [Python] 数据结构 详解及代码 AIAdvocate 算法python数据结构链表
    今日内容大纲介绍数据结构介绍列表链表1.数据结构和算法简介程序大白话翻译,程序=数据结构+算法数据结构指的是存储,组织数据的方式.算法指的是为了解决实际业务问题而思考思路和方法,就叫:算法.2.算法的5大特性介绍算法具有独立性算法是解决问题的思路和方式,最重要的是思维,而不是语言,其(算法)可以通过多种语言进行演绎.5大特性有输入,需要传入1或者多个参数有输出,需要返回1个或者多个结果有穷性,执行
  • Python算法L5：贪心算法 小熊同学哦 Python算法算法python贪心算法
    Python贪心算法简介目录Python贪心算法简介贪心算法的基本步骤贪心算法的适用场景经典贪心算法问题1.**零钱兑换问题**2.**区间调度问题**3.**背包问题**贪心算法的优缺点优点：缺点：结语贪心算法（GreedyAlgorithm）是一种在每一步选择中都采取当前最优或最优解的算法。它的核心思想是，在保证每一步局部最优的情况下，希望通过贪心选择达到全局最优解。虽然贪心算法并不总能得到全
  • 【RabbitMQ 项目】服务端：数据管理模块之绑定管理 月夜星辉雪 rabbitmq分布式
    文章目录一.编写思路二.代码实践一.编写思路定义绑定信息类交换机名称队列名称绑定关键字：交换机的路由交换算法中会用到没有是否持久化的标志，因为绑定是否持久化取决于交换机和队列是否持久化，只有它们都持久化时绑定才需要持久化。绑定就好像一根绳子，两端连接着交换机和队列，当一方不存在，它就没有存在的必要了定义绑定持久化类构造函数：如果数据库文件不存在则创建，打开数据库，创建binding_table插入
  • 非对称加密算法原理与应用2——RSA私钥加密文件 私语茶馆 云部署与开发架构及产品灵感记录RSA2048私钥加密
    作者：私语茶馆1.相关章节（1）非对称加密算法原理与应用1——秘钥的生成-CSDN博客第一章节讲述的是创建秘钥对，并将公钥和私钥导出为文件格式存储。本章节继续讲如何利用私钥加密内容，包括从密钥库或文件中读取私钥，并用RSA算法加密文件和String。2.私钥加密的概述本文主要基于第一章节的RSA2048bit的非对称加密算法讲述如何利用私钥加密文件。这种加密后的文件，只能由该私钥对应的公钥来解密。
  • 粒子群优化 (PSO) 在三维正弦波函数中的应用 subject625Ruben 机器学习人工智能matlab算法
    在这篇博客中，我们将展示如何使用粒子群优化（PSO）算法求解三维正弦波函数，并通过增加正弦波扰动，使优化过程更加复杂和有趣。本文将介绍目标函数的定义、PSO参数设置以及算法执行的详细过程，并展示搜索空间中的动态过程和收敛曲线。1.目标函数定义我们使用的目标函数是一个三维正弦波函数，定义如下：objectiveFunc=@(x)sin(sqrt(x(1).^2+x(2).^2))+0.5*sin(5
  • 非对称加密算法————RSA理论及详情 hu19930613
    转自：https://www.kancloud.cn/kancloud/rsa_algorithm/48484一、一点历史1976年以前，所有的加密方法都是同一种模式：（1）甲方选择某一种加密规则，对信息进行加密；（2）乙方使用同一种规则，对信息进行解密。由于加密和解密使用同样规则（简称"密钥"），这被称为"对称加密算法"（Symmetric-keyalgorithm）。这种加密模式有一个最大弱点
  • ai绘画工具midjourney怎么下载？附作品管理教程 设计师早上好
    Midjourney是一款功能强大的AI绘画工具，它使用机器学习技术和深度神经网络等算法，可以生成各种艺术风格的绘画作品。在创意设计、广告宣传等方面有着广泛的应用前景。那么，ai绘画工具midjourney怎么下载？本文将为您介绍Midjourney的下载以及作品的相关管理。一、Midjourney下载Midjourney的下载非常简单，只需打开Midjourney官网（点击“GetMidjour
  • 【加密算法基础——对称加密和非对称加密】 XWWW668899 网络安全服务器笔记
    对称加密与非对称加密对称加密和非对称加密是两种基本的加密方法，各自有不同的特点和用途。以下是详细比较：1.对称加密特点密钥:使用相同的密钥进行加密和解密。发送方和接收方必须共享这个密钥。速度:通常速度较快，适合处理大量数据。实现:算法相对简单，计算效率高。常见算法AES(高级加密标准)DES(数据加密标准)3DES(三重数据加密标准)RC4(流密码)应用场景文件加密磁盘加密传输大量数据时的加密2.
  • 【算法练习】IDEA集成leetcode插件实现快速刷 2401_84102892 2024年程序员学习算法intellij-idealeetcode
    ============点击右侧边leetcode->设置->配置地址、用户名、密码、存放目录、文件模板用户名要登录后在账号信息里看模板代码1.codefilename!velocityTool.camelC
  • 【加密算法基础——RSA 加密】 XWWW668899 网络服务器笔记python
    RSA加密RSA（Rivest-Shamir-Adleman）加密是非对称加密，一种广泛使用的公钥加密算法，主要用于安全数据传输。公钥用于加密，私钥用于解密。RSA加密算法的名称来源于其三位发明者的姓氏：R:RonRivestS:AdiShamirA:LeonardAdleman这三位计算机科学家在1977年共同提出了这一算法，并发表了相关论文。他们的工作为公钥加密的基础奠定了重要基础，使得安全通
  • 机器学习-聚类算法 不良人龍木木 机器学习机器学习算法聚类
    机器学习-聚类算法1.AHC2.K-means3.SC4.MCL仅个人笔记，感谢点赞关注！1.AHC2.K-means3.SC传统谱聚类：个人对谱聚类算法的理解以及改进4.MCL目前仅专注于NLP的技术学习和分享感谢大家的关注与支持！
  • 生成式地图制图 Bwywb_3 深度学习机器学习深度学习生成对抗网络
    生成式地图制图（GenerativeCartography）是一种利用生成式算法和人工智能技术自动创建地图的技术。它结合了传统的地理信息系统（GIS）技术与现代生成模型（如深度学习、GANs等），能够根据输入的数据自动生成符合需求的地图。这种方法在城市规划、虚拟环境设计、游戏开发等多个领域具有应用前景。主要特点：自动化生成：通过算法和模型，系统能够根据输入的地理或空间数据自动生成地图，而无需人工逐
  • 高性能javascript--算法和流程控制 海淀萌狗
    -for,while和do-while性能相当-避免使用for-in循环，==除非遍历一个属性量未知的对象==es5:for-in遍历的对象便不局限于数组，还可以遍历对象。原因：for-in每次迭代操作会同时搜索实例或者原型属性，for-in循环的每次迭代都会产生更多开销，因此要比其他循环类型慢，一般速度为其他类型循环的1/7。因此，除非明确需要迭代一个属性数量未知的对象，否则应避免使用for-i
  • 深度 Qlearning：在直播推荐系统中的应用 AGI通用人工智能之禅 程序员提升自我硅基计算碳基计算认知计算生物计算深度学习神经网络大数据AIGCAGILLMJavaPython架构设计Agent程序员实现财富自由
    深度Q-learning：在直播推荐系统中的应用关键词：深度Q-learning,强化学习,直播推荐系统,个性化推荐1.背景介绍1.1问题的由来随着互联网技术的飞速发展,直播平台如雨后春笋般涌现。面对海量的直播内容,用户很难快速找到自己感兴趣的内容。因此,个性化推荐系统在直播平台中扮演着越来越重要的角色。1.2研究现状目前,主流的个性化推荐算法包括协同过滤、基于内容的推荐等。这些方法在一定程度上缓
  • JVM源码分析之堆外内存完全解读 HeapDump性能社区
    概述广义的堆外内存说到堆外内存，那大家肯定想到堆内内存，这也是我们大家接触最多的，我们在jvm参数里通常设置-Xmx来指定我们的堆的最大值，不过这还不是我们理解的Java堆，-Xmx的值是新生代和老生代的和的最大值，我们在jvm参数里通常还会加一个参数-XX:MaxPermSize来指定持久代的最大值，那么我们认识的Java堆的最大值其实是-Xmx和-XX:MaxPermSize的总和，在分代算法
  • 《算法》四学习——1.1节 进阶的Farmer 算法算法笔记
    前言买了一本算法4，每天看一点，对每个小结来个学习总结，输出驱动输入。本篇笔记针对第一章基础1.1基础编程模型1.1节总结了相关的语法、语言特性和书中将会用到的库。笔记自己在编码中容易遗漏的点&&优先级比||高在开发中习惯了加括号，所以没注意到这点，教材上也有但是忘记了二分查找中计算mid=left+(right-left)/2这样计算可以有效避免(left+right)/2溢出答疑java无穷大
  • 排序 路小白同学
    1.冒泡排序冒泡算法是一种基础的排序算法，这种算法会重复的比较数组中相邻的两个元素。如果一个元素比另一个元素大（小），那么就交换这两个元素的位置。重复这一比较直至最后一个元素。这一比较会重复n-1趟，每一趟比较n-j次，j是已经排序好的元素个数。每一趟比较都能找出未排序元素中最大或者最小的那个数字。这就如同水泡从水底逐个飘到水面一样。冒泡排序是一种时间复杂度较高，效率较低的排序方法。其空间复杂度是
  • jvm调优总结（从基本概念 到 深度优化） oloz javajvmjdk虚拟机应用服务器
    JVM参数详解：http://www.cnblogs.com/redcreen/archive/2011/05/04/2037057.html   Java虚拟机中，数据类型可以分为两类：基本类型和引用类型。基本类型的变量保存原始值，即：他代表的值就是数值本身；而引用类型的变量保存引用值。“引用值”代表了某个对象的引用，而不是对象本身，对象本身存放在这个引用值所表示的地址的位置。
  • 【Scala十六】Scala核心十：柯里化函数 bit1129 scala
    本篇文章重点说明什么是函数柯里化，这个语法现象的背后动机是什么，有什么样的应用场景，以及与部分应用函数(Partial Applied Function)之间的联系   1. 什么是柯里化函数 A way to write functions with multiple parameter lists. For instance def f(x: Int)(y: Int) is a
  • HashMap dalan_123 java
    HashMap在java中对很多人来说都是熟的；基于hash表的map接口的非同步实现。允许使用null和null键；同时不能保证元素的顺序；也就是从来都不保证其中的元素的顺序恒久不变。 1、数据结构     在java中，最基本的数据结构无外乎：数组 和 引用（指针），所有的数据结构都可以用这两个来构造，HashMap也不例外，归根到底HashMap就是一个链表散列的数据
  • Java Swing如何实时刷新JTextArea，以显示刚才加append的内容 周凡杨 java更新swingJTextArea
    在代码中执行完textArea.append("message")后，如果你想让这个更新立刻显示在界面上而不是等swing的主线程返回后刷新，我们一般会在该语句后调用textArea.invalidate()和textArea.repaint()。 问题是这个方法并不能有任何效果，textArea的内容没有任何变化，这或许是swing的一个bug，有一个笨拙的办法可以实现
  • servlet或struts的Action处理ajax请求 g21121 servlet
    其实处理ajax的请求非常简单，直接看代码就行了： //如果用的是struts //HttpServletResponse response = ServletActionContext.getResponse(); // 设置输出为文字流 response.setContentType("text/plain"); // 设置字符集 res
  • FineReport的公式编辑框的语法简介 老A不折腾 finereport公式总结
    FINEREPORT用到公式的地方非常多，单元格（以=开头的便被解析为公式），条件显示，数据字典，报表填报属性值定义，图表标题，轴定义，页眉页脚，甚至单元格的其他属性中的鼠标悬浮提示内容都可以写公式。 简单的说下自己感觉的公式要注意的几个地方：   1.if语句语法刚接触感觉比较奇怪，if(条件式子,值1,值2)，if可以嵌套，if(条件式子1，值1，if(条件式子2，值2，值3)
  • linux mysql 数据库乱码的解决办法 墙头上一根草 linuxmysql数据库乱码
    linux 上mysql数据库区分大小写的配置 lower_case_table_names=1 1-不区分大小写 0-区分大小写   修改/etc/my.cnf 具体的修改内容如下:   [client] default-character-set=utf8   [mysqld] datadir=/var/lib/mysql socket=/va
  • 我的spring学习笔记6-ApplicationContext实例化的参数兼容思想 aijuans Spring 3
    ApplicationContext能读取多个Bean定义文件，方法是： ApplicationContext appContext = new ClassPathXmlApplicationContext（ new String[]｛“bean-config1.xml”，“bean-config2.xml”，“bean-config3.xml”，“bean-config4.xml
  • mysql 基准测试之sysbench annan211 基准测试mysql基准测试MySQL测试sysbench
    1 执行如下命令，安装sysbench-0.5： tar xzvf sysbench-0.5.tar.gz  cd sysbench-0.5  chmod +x autogen.sh  ./autogen.sh  ./configure --with-mysql --with-mysql-includes=/usr/local/mysql
  • sql的复杂查询使用案列与技巧 百合不是茶 oraclesql函数数据分页合并查询
      本片博客使用的数据库表是oracle中的scott用户表;          -------------------  自然连接查询           查询 smith 的上司(两种方法) &
  • 深入学习Thread类 bijian1013 javathread多线程java多线程
    一．             线程的名字 下面来看一下Thread类的name属性，它的类型是String。它其实就是线程的名字。在Thread类中，有String getName()和void setName(String)两个方法用来设置和获取这个属性的值。 同时，Thr
  • JSON串转换成Map以及如何转换到对应的数据类型 bijian1013 javafastjsonnet.sf.json
            在实际开发中，难免会碰到JSON串转换成Map的情况，下面来看看这方面的实例。另外，由于fastjson只支持JDK1.5及以上版本，因此在JDK1.4的项目中可以采用net.sf.json来处理。 一.fastjson实例 JsonUtil.java package com.study; impor
  • 【RPC框架HttpInvoker一】HttpInvoker：Spring自带RPC框架 bit1129 spring
    HttpInvoker是Spring原生的RPC调用框架，HttpInvoker同Burlap和Hessian一样，提供了一致的服务Exporter以及客户端的服务代理工厂Bean，这篇文章主要是复制粘贴了Hessian与Spring集成一文，【RPC框架Hessian四】Hessian与Spring集成   在 【RPC框架Hessian二】Hessian 对象序列化和反序列化一文中
  • 【Mahout二】基于Mahout CBayes算法的20newsgroup的脚本分析 bit1129 Mahout
    #!/bin/bash # # Licensed to the Apache Software Foundation (ASF) under one or more # contributor license agreements. See the NOTICE file distributed with # this work for additional information re
  • nginx三种获取用户真实ip的方法 ronin47
    随着nginx的迅速崛起，越来越多公司将apache更换成nginx. 同时也越来越多人使用nginx作为负载均衡, 并且代理前面可能还加上了CDN加速，但是随之也遇到一个问题：nginx如何获取用户的真实IP地址,如果后端是apache,请跳转到<apache获取用户真实IP地址>，如果是后端真实服务器是nginx，那么继续往下看。 实例环境： 用户IP 120.22.11.11
  • java-判断二叉树是不是平衡 bylijinnan java
    参考了 http://zhedahht.blog.163.com/blog/static/25411174201142733927831/ 但是用java来实现有一个问题。 由于Java无法像C那样“传递参数的地址，函数返回时能得到参数的值”，唯有新建一个辅助类：AuxClass import ljn.help.*; public class BalancedBTree {
  • BeanUtils.copyProperties VS PropertyUtils.copyProperties 诸葛不亮 PropertyUtilsBeanUtils
     BeanUtils.copyProperties VS  PropertyUtils.copyProperties  作为两个bean属性copy的工具类，他们被广泛使用，同时也很容易误用，给人造成困然；比如：昨天发现同事在使用BeanUtils.copyProperties copy有integer类型属性的bean时，没有考虑到会将null转换为0，而后面的业
  • [金融与信息安全]最简单的数据结构最安全 comsci 数据结构
          现在最流行的数据库的数据存储文件都具有复杂的文件头格式，用操作系统的记事本软件是无法正常浏览的，这样的情况会有什么问题呢？        从信息安全的角度来看，如果我们数据库系统仅仅把这种格式的数据文件做异地备份，如果相同版本的所有数据库管理系统都同时被攻击，那么
  • vi区段删除 Cwind linuxvi区段删除
    区段删除是编辑和分析一些冗长的配置文件或日志文件时比较常用的操作。简记下vi区段删除要点备忘。   vi概述    引文中并未将末行模式单独列为一种模式。单不单列并不重要，能区分命令模式与末行模式即可。   vi区段删除步骤： 1. 在末行模式下使用:set nu显示行号 非必须，随光标移动vi右下角也会显示行号，能够正确找到并记录删除开始行
  • 清除tomcat缓存的方法总结 dashuaifu tomcat缓存
    用tomcat容器，大家可能会发现这样的问题，修改jsp文件后，但用IE打开 依然是以前的Jsp的页面。 出现这种现象的原因主要是tomcat缓存的原因。 解决办法如下: 在jsp文件头加上 <meta http-equiv="Expires" content="0"> <meta http-equiv="kiben&qu
  • 不要盲目的在项目中使用LESS CSS dcj3sjt126com Webless
    　如果你还不知道LESS CSS是什么东西，可以看一下这篇文章，是我一朋友写给新人看的《CSS——LESS》 　　不可否认，LESS CSS是个强大的工具，它弥补了css没有变量、无法运算等一些“先天缺陷”，但它似乎给我一种错觉，就是为了功能而实现功能。 　　比如它的引用功能 ? .rounded_corners{     
  • [入门]更上一层楼 dcj3sjt126com PHPyii2
    更上一层楼 通篇阅读完整个“入门”部分，你就完成了一个完整 Yii 应用的创建。在此过程中你学到了如何实现一些常用功能，例如通过 HTML 表单从用户那获取数据，从数据库中获取数据并以分页形式显示。你还学到了如何通过 Gii 去自动生成代码。使用 Gii 生成代码把 Web 开发中多数繁杂的过程转化为仅仅填写几个表单就行。 本章将介绍一些有助于更好使用 Yii 的资源：
  • Apache HttpClient使用详解 eksliang httpclienthttp协议
    Http协议的重要性相信不用我多说了，HttpClient相比传统JDK自带的URLConnection，增加了易用性和灵活性（具体区别，日后我们再讨论），它不仅是客户端发送Http请求变得容易，而且也方便了开发人员测试接口（基于Http协议的），即提高了开发的效率，也方便提高代码的健壮性。因此熟练掌握HttpClient是很重要的必修内容，掌握HttpClient后，相信对于Http协议的了解会
  • zxing二维码扫描功能 gundumw100 androidzxing
    经常要用到二维码扫描功能 现给出示例代码 import com.google.zxing.WriterException; import com.zxing.activity.CaptureActivity; import com.zxing.encoding.EncodingHandler; import android.app.Activity; import an
  • 纯HTML+CSS带说明的黄色导航菜单 ini htmlWebhtml5csshovertree
    HoverTree带说明的CSS菜单:纯HTML+CSS结构链接带说明的黄色导航   在线体验效果：http://hovertree.com/texiao/css/1.htm代码如下,保存到HTML文件可以看到效果：   <!DOCTYPE html > <html > <head> <title>HoverTree
  • fastjson初始化对性能的影响 kane_xie fastjson序列化
    之前在项目中序列化是用thrift，性能一般，而且需要用编译器生成新的类，在序列化和反序列化的时候感觉很繁琐，因此想转到json阵营。对比了jackson，gson等框架之后，决定用fastjson，为什么呢，因为看名字感觉很快。。。   网上的说法：   fastjson 是一个性能很好的 Java 语言实现的 JSON 解析器和生成器，来自阿里巴巴的工程师开发。
  • 基于Mybatis封装的增删改查实现通用自动化sql mengqingyu DAO
    1.基于map或javaBean的增删改查可实现不写dao接口和实现类以及xml，有效的提高开发速度。 2.支持自定义注解包括主键生成、列重复验证、列名、表名等 3.支持批量插入、批量更新、批量删除 <bean id="dynamicSqlSessionTemplate" class="com.mqy.mybatis.support.Dynamic
  • js控制input输入框的方法封装(数字，中文，字母，浮点数等) qifeifei javascript js
    在项目开发的时候，经常有一些输入框，控制输入的格式，而不是等输入好了再去检查格式，格式错了就报错，体验不好。 /** 数字，中文，字母,浮点数(+/-/.) 类型输入限制，只要在input标签上加上 jInput="number,chinese,alphabet,floating" 备注：floating属性只能单独用*/     funct
  • java 计时器应用 tangqi609567707 javatimer
    mport java.util.TimerTask;   import java.util.Calendar;   public class MyTask extends TimerTask {        private static final int
  • erlang输出调用栈信息 wudixiaotie erlang
    在erlang otp的开发中，如果调用第三方的应用，会有有些错误会不打印栈信息，因为有可能第三方应用会catch然后输出自己的错误信息，所以对排查bug有很大的阻碍，这样就要求我们自己打印调用的栈信息。用这个函数：erlang:process_display (self (), backtrace).需要注意这个函数只会输出到标准错误输出。 也可以用这个函数：erlang:get_s
按字母分类： ABCDEFGHIJKLMNOPQRSTUVWXYZ其他