二叉树的直径 diameter-of-binary-tree, BFS/DFS

* Tree.h

//
// Created by EDZ on 2021/4/2.
//

#ifndef DIAMETEROFTREE_TREE_H
#define DIAMETEROFTREE_TREE_H
#include "deque"

//#ifndef max
//#define max(a, b) ((a) > (b) ? (a) : (b))
//#endif

template
T max(T a, T b) {
    return a > b ? a : b;
}

template class Node {
public:
    explicit Node(T val) {
        this->val = val;
        this->left = nullptr;
        this->right = nullptr;
    }
    Node *setLeft(Node *node) {this->left = node; return this;}
    Node *setRight(Node *node) {this->right = node; return this;}
    Node *getLeft() {return this->left;}
    Node *getRight() {return this->right;}
    T getValue() {return this->val;}
    static void preOrderTraverse(Node *node, void (*fn)(T)) {
        if (node == nullptr) {
            return;
        }
        fn(node->getValue());
        preOrderTraverse(node->left, fn);
        preOrderTraverse(node->right, fn);
    }
    static int maxDepth(Node *root) {
        if (root == nullptr) {return 0;}
        return 1 + max(maxDepth(root->left), maxDepth(root->right));
    }
    static int diameterOfBinaryTree(Node* root) {
        if (root == nullptr) {return 0;}
        int ans = maxDepth(root->left) + maxDepth(root->right);
        return max(ans, max(diameterOfBinaryTree(root->left), diameterOfBinaryTree(root->right)));
    }
    /**
     * 记录左子树的最大深度或者是右子树的最大深度
     * @param root
     * @param res
     * @return
     */
    static T helper(Node *root, int &res) {
        if (!root) {return 0;}
        int left = helper(root->left, res);
        int right = helper(root->right, res);
        left = root->left ? left + 1 : left;
        right = root->right ? right + 1 : right;
        res = max(res, right + left);
        return max(left, right);
    }
private:
    Node *left;
    Node *right;
    T val;
};

template class Tree {
public:
    Tree() {this->root = nullptr;}
    explicit Tree(Node *root) {this->root = root;}
    Node *getRoot() {return this->root;}
    void preOrderTraverse(void (*fn)(T)) {
        Node::preOrderTraverse(this->getRoot(), fn);
    }
    int maxDepth() {return Node::maxDepth(this->root);}
    int diameterOfBinaryTree() {
        // return Node::diameterOfBinaryTree(this->root);
        int ans = 0;
        Node::helper(root, ans);
        return ans;
    }
    /**
     * 按层级遍历二叉树
     * https://blog.csdn.net/hansionz/article/details/81947834
     * https://blog.csdn.net/fareast_mzh/article/details/109709882
     * @param fn
     */
    void levelTraverse(void (*fn)(T)) {
        // 树为空，直接返回
        if (this->getRoot() == nullptr) {return;}
        std::deque *> q;
        // 先将根节点入队
        q.push_back(this->getRoot());
        Node *front;
        Node *left, *right;
        while (!q.empty()) {
            // 保存队头并访问, 出队
            front = q.front();
            fn(front->getValue());
            q.pop_front();
            // 将出队节点的左子树根入队
            left = front->getLeft();
            if (left != nullptr) {
                q.push_back(left);
            }
            // 将出队节点的右子树根入队
            right = front->getRight();
            if (right != nullptr) {
                q.push_back(right);
            }
        }
    }
private:
    Node *root;
};

#endif //DIAMETEROFTREE_TREE_H

* main.cpp

#include 
#include "Tree.h"

int main() {
    auto *node = new Node(1);
    node->setLeft((new Node(2))
            ->setLeft(new Node(4))
            ->setRight(new Node(5)));
    node->setRight((new Node(3)));
//            ->setLeft((new Node(6))
//              ->setLeft(new Node(8))
//              ->setRight(new Node(9)))
//            ->setRight(new Node(7)));

    Tree t = Tree(node);

    auto fn = [](int v) {std::cout << v << ",";};
    t.levelTraverse(fn);  // 按层级遍历
    std::cout << "\n";
    t.preOrderTraverse(fn); // 先序遍历
    std::cout <<"\n";
    // 二叉树的深度
    std::cout << "Depth=" << t.maxDepth() << "\n";
    // 二叉树的直径
    std::cout << "Diameter=" << t.diameterOfBinaryTree() <<"\n";

    return 0;
}

* CMakeLists.h

cmake_minimum_required(VERSION 3.17)
project(DiameterOfTree)

set(CMAKE_CXX_STANDARD 14)

add_executable(DiameterOfTree main.cpp Tree.h)

CLion, MinGW配置:

Window10上CLion极简配置教程 - 简书

MinGW下载:

MinGW-w64 - for 32 and 64 bit Windows - Browse /Toolchains targetting Win64/Personal Builds/mingw-builds at SourceForge.net

不要点绿色的按钮 不要点 Online Installer， 在线下载外国的网站速度慢，直接下载 .7z压缩包

百度网盘:

下载链接：百度网盘 请输入提取码
密码：obb8

或者我的资源:windows环境gcc/g++mingw64.zip-C++文档类资源-CSDN下载

Clion

https://download.jetbrains.8686c.com/cpp/CLion-2020.3.3.exe

如果试用期到了:

Binary Tree 非递归方式实现二叉树先序遍历、中序遍历、后续遍历， 按层级遍历 BinarySearchTree, Java, reset.vbs Jetbrains_fareast_mzh的博客-CSDN博客

拖到底部, 执行reset脚本

来自leetcode

力扣

/**
 * Definition for a binary tree node.
 * function TreeNode(val, left, right) {
 *     this.val = (val===undefined ? 0 : val)
 *     this.left = (left===undefined ? null : left)
 *     this.right = (right===undefined ? null : right)
 * }
 */
/**
 * @param {TreeNode} root
 * @return {number}
 */
var diameterOfBinaryTree = function(root) {    
    if (!root) {
        return 1;
    }
    var max = 0;
    var dfs = function(node) {
        if (!node) {return 0;}
        var lh = dfs(node.left);
        var rh = dfs(node.right);
        max = Math.max(max, lh + rh);
        return Math.max(lh, rh) + 1;
    } 
    dfs(root);
    return max;
};

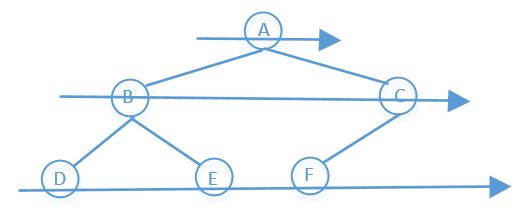
BFS(宽度优先搜索(又称广度优先搜索))

他的访问顺序是：先访问上一层，在访问下一层，一层一层的往下访问

所以上图前序遍历的结果是：A→B→C→D→E→F

访问顺序如下

代码如下

 1public static void levelOrder(TreeNode tree) {
 2    if (tree == null)
 3        return;
 4    LinkedList list = new LinkedList<>();//链表，这里我们可以把它看做队列
 5    list.add(tree);//相当于把数据加入到队列尾部
 6    while (!list.isEmpty()) {
 7        TreeNode node = list.poll();//poll方法相当于移除队列头部的元素
 8        System.out.println(node.val);
 9        if (node.left != null)
10            list.add(node.left);
11        if (node.right != null)
12            list.add(node.right);
13    }
14}

递归的写法

 1public static void levelOrder(TreeNode tree) {
 2    int depth = depth(tree);
 3    for (int level = 0; level < depth; level++) {
 4        printLevel(tree, level);
 5    }
 6}
 7
 8private static int depth(TreeNode tree) {
 9    if (tree == null)
10        return 0;
11    int leftDepth = depth(tree.left);
12    int rightDepth = depth(tree.right);
13    return Math.max(leftDepth, rightDepth) + 1;
14}
15
16
17private static void printLevel(TreeNode tree, int level) {
18    if (tree == null)
19        return;
20    if (level == 0) {
21        System.out.print(" " + tree.val);
22    } else {
23        printLevel(tree.left, level - 1);
24        printLevel(tree.right, level - 1);
25    }
26}

如果想把遍历的结果存放到list中，我们还可以这样写

 1public static List> levelOrder(TreeNode tree) {
 2    if (tree == null)
 3        return null;
 4    List> list = new ArrayList<>();
 5    bfs(tree, 0, list);
 6    return list;
 7}
 8
 9private static void bfs(TreeNode tree, int level, List> list) {
10    if (tree == null)
11        return;
12    if (level >= list.size()) {
13        List subList = new ArrayList<>();
14        subList.add(tree.val);
15        list.add(subList);
16    } else {
17        list.get(level).add(tree.val);
18    }
19    bfs(tree.left, level + 1, list);
20    bfs(tree.right, level + 1, list);
21}

05

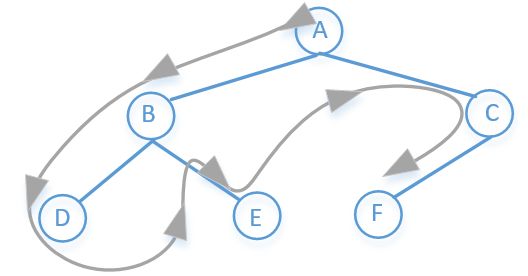
DFS(深度优先搜索)

他的访问顺序是：先访根节点，然后左结点，一直往下，直到最左结点没有子节点的时候然后往上退一步到父节点，然后父节点的右子节点在重复上面步骤……

所以上图前序遍历的结果是：A→B→D→E→C→F

访问顺序如下

代码如下

 1public static void treeDFS(TreeNode root) {
 2    Stack stack = new Stack<>();
 3    stack.add(root);
 4    while (!stack.empty()) {
 5        TreeNode node = stack.pop();
 6        System.out.println(node.val);
 7        if (node.right != null) {
 8            stack.push(node.right);
 9        }
10        if (node.left != null) {
11            stack.push(node.left);
12        }
13    }
14}

递归的写法

1public static void treeDFS(TreeNode root) {
2    if (root == null)
3        return;
4    System.out.println(root.val);
5    treeDFS(root.left);
6    treeDFS(root.right);
7}