力扣LeetBook＜二叉树＞学习笔记

二叉树

一、概述

从图的观点：树是一个拥有N个结点和N-1条边的有向无环图。
二叉树：每个节点最多有两个子树。

二、树的遍历

前序：根-左-右
中序：左-根-右（对于二叉搜索树，我们可以通过中序遍历得到一个递增的有序序列。）
后序：左-右-根（删除树中的节点）
层序：逐层遍历树结构（BFS:从一个根节点开始，首先访问节点本身。 然后遍历它的相邻节点，其次遍历它的二级邻节点、三级邻节点，以此类推）

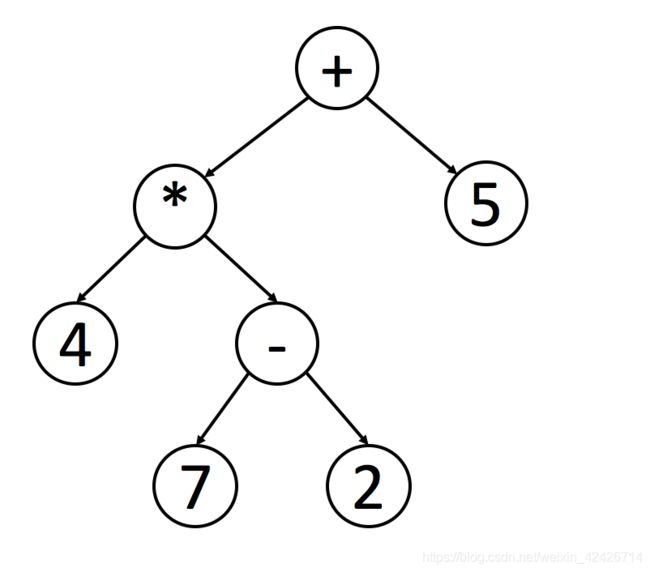
如图，使用中序遍历找出原始表达式，但程序不好处理这个表达式，因为必须检查优先级。
如果想后序遍历，使用栈来处理这个表达式会更容易。每遇到一个操作符，就从栈中弹出栈顶的两个元素，计算并将结果返回栈中。

1.二叉树的前序遍历

144.二叉树的前序遍历
法1：递归
发现递归有三点注意，落实好就行。针对这道题而言，

1. 终止条件：当越过叶节点，即(root == null)则直接返回
2. 递推工作：当list添加元素后，开启递归左子结点，无返回值；再开启递归右子结点，无返回值
3. 返回值：这里不需要返回值

    public List<Integer> preorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        preorderTraversal(root, list);
        return list;
    }

    private void preorderTraversal(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        list.add(root.val);
        preorderTraversal(root.left, list);
        preorderTraversal(root.right, list);
//        if (root != null) {
//            list.add(root.val);
//            preorderTraversal(root.left, list);
//            preorderTraversal(root.right, list);
//        }
    }

注释掉的内容是可以代替上面部分的。
法2：迭代
递归法是隐式调用了系统栈，迭代法则是创建了一个显式内置栈来模拟系统栈。通常比递归麻烦，因为是我们自己来操纵栈的一举一动了。

    // 前序:根左右
    public List<Integer> preorderTraversal1(TreeNode root) {
        List<Integer> res = new ArrayList<Integer>();
//        if (root == null) {
//            return res;
//        }
        Deque<TreeNode> stack = new LinkedList<TreeNode>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                res.add(node.val);
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            node = node.right;
        }
        return res;
    }

2.二叉树的中序遍历

法1：递归

    public List<Integer> inorderTraversal(TreeNode root) {
        List<Integer> list = new ArrayList<>();
        inorderTraversal(root, list);
        return list;
    }

    private void inorderTraversal(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        inorderTraversal(root.left, list);
        list.add(root.val);
        inorderTraversal(root.right, list);
    }

法2：迭代

    // 中序：左根右
    public List<Integer> inorderTraversal1(TreeNode root) {
        List<Integer> res = new ArrayList<>();
//        if (root == null) {
//            return res;
//        }
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode node = root;
        while (!stack.isEmpty() || node != null) {
            while (node != null) {
                stack.push(node);
                node = node.left;
            }
            node = stack.pop();
            res.add(node.val);
            node = node.right;
        }
        return res;
    }

3.二叉树的后序遍历

法1：递归

    public List<Integer> postorderTraversal(TreeNode root) {
        // 递归
        List<Integer> list = new ArrayList<>();
        postorderTraversal(root, list);
        return list;
    }

    private void postorderTraversal(TreeNode root, List<Integer> list) {
        if (root == null) {
            return;
        }
        postorderTraversal(root.left, list);
        postorderTraversal(root.right, list);
        list.add(root.val);
    }

法2：迭代

    // 后序：左右根
    public List<Integer> postorderTraversal1(TreeNode root) {
        List<Integer> res = new ArrayList<>();
        Deque<TreeNode> stack = new LinkedList<>();
        TreeNode prev = null;
        while (!stack.isEmpty() || root != null) {
            while (root != null) {
                stack.push(root);
                root = root.left;
            }
            root = stack.pop();
            if (root.right == null || root.right == prev) {
                res.add(root.val);
                prev = root;
                root = null;
            } else {
                stack.push(root);
                root = root.right;
            }
        }
        return res;
    }

4.二叉树的层序遍历

102. 二叉树的层序遍历

    // 层序
    public List<List<Integer>> levelOrder(TreeNode root) {
        List<List<Integer>> res = new ArrayList<>();
        if (root == null) {
            return res;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);// 起点：root
        while (!queue.isEmpty()) {
            List<Integer> level = new ArrayList<>();
            int sz = queue.size();
            for (int i = 0; i < sz; i++) {
                TreeNode node = queue.poll();
                level.add(node.val);
                if (node.left != null) {
                    queue.offer(node.left);
                }
                if (node.right != null) {
                    queue.offer(node.right);
                }
            }
            res.add(level);
        }
        return res;
    }

三、运用递归解决问题

1.二叉树的最大深度

104.二叉树的最大深度
法1：递归

    public int maxDepth(TreeNode root) {
        return root == null ? 0 : Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
    }

当然我不喜欢写成这样,虽然极简,但我更喜欢看到有秩序的递归:

    public int maxDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        int depth = Math.max(maxDepth(root.left), maxDepth(root.right)) + 1;
        return depth;
    }

甚至可以再详细点，让人一目了然的那种。

        int leftDepth = maxDepth(root.left) + 1;
        int rightDepth = maxDepth(root.right) + 1;
        int maxDepth = Math.max(leftDepth, rightDepth);
        return maxDepth;

这样可读性就提高了啦~

法2：BFS

    public int maxDepth1(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 0;
        while (!queue.isEmpty()) {
            int sz = queue.size();
            for (int i = 0; i < sz; i++) {
                TreeNode cur = queue.poll();
//                if (cur.left == null && cur.right == null) {
//                    continue;
//                }
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            depth++;
        }
        return depth;
    }

可以对比一下最小深度：
111. 二叉树的最小深度
法1：递归

    public int minDepth1(TreeNode root) {
        //1.根为空（已经越过叶子节点）
        if (root == null)
            return 0;
        //2.左右子树都为空（叶子节点）
        if (root.left == null && root.right == null)
            return 1;
        //3.左子树右子树有一个为空，取不是空的方向。
        //4.左右子树都不为空，就取两个子树深度较小的，最后加1.
        int depth = Integer.MAX_VALUE;
        if (root.left != null)
            depth = Math.min(minDepth(root.left), depth);
        if (root.right != null)
            depth = Math.min(minDepth(root.right), depth);
        return depth + 1;
    }

法2：BFS

    public int minDepth(TreeNode root) {
        if (root == null) {
            return 0;
        }
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(root);
        int depth = 1;
        while (!queue.isEmpty()) {
            int sz = queue.size();
            for (int i = 0; i < sz; i++) {
                TreeNode cur = queue.poll();
                if (cur.left == null && cur.right == null) {
                    return depth;
                }
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
            }
            depth++;
        }
        return depth;
    }

2.对称二叉树

101.对称二叉树

1. 递归结束条件：

• 都为null返回true
• 只有一个为null返回false

2. 递归过程

• 两个节点值是否相等
• n1的左子树和n2的右子树是否对称
• n1的右子树和n2的左子树是否对称

法1：

    public boolean isSymmetric(TreeNode root) {
        return isMirror(root, root);
    }

    public boolean isMirror(TreeNode n1, TreeNode n2) {
        if (n1 == null && n2 == null) {
            return true;
        }
        if (n1 == null || n2 == null) {
            return false;
        }
        return n1.val == n2.val && isMirror(n1.left, n2.right) && isMirror(n1.right, n2.left);
    }

法2：

    public boolean isSymmetric1(TreeNode root) {
        return isMirror(root, root);
    }

    public boolean isMirror(TreeNode n1, TreeNode n2) {
        Queue<TreeNode> queue = new LinkedList<>();
        queue.offer(n1);
        queue.offer(n2);
        while (!queue.isEmpty()) {
            n1 = queue.poll();
            n2 = queue.poll();
            if (n1 == null && n2 == null)
                continue;
            if (n1 == null || n2 == null || n1.val != n2.val)
                return false;

            queue.offer(n1.left);
            queue.offer(n2.right);
            queue.offer(n1.right);
            queue.offer(n2.left);
        }
        return true;
    }

3.路径总和

112.路径总和
法1：

    public boolean hasPathSum(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        if (root.left == null && root.right == null) {
            return sum == root.val;
        }
        return hasPathSum(root.left, sum - root.val) || hasPathSum(root.right, sum - root.val);
    }

法2：

    public boolean hasPathSum1(TreeNode root, int sum) {
        if (root == null) {
            return false;
        }
        Queue<TreeNode> nodeQueue = new LinkedList<>();
        Queue<Integer> valQueue = new LinkedList<>();
        nodeQueue.offer(root);
        valQueue.offer(root.val);
        while (!nodeQueue.isEmpty()) {
            TreeNode cur = nodeQueue.poll();
            int temp = valQueue.poll();
            if (cur.left == null && cur.right == null) {
                if (sum == temp) {
                    return true;
                }
                continue;
            }
            if (cur.left != null) {
                nodeQueue.offer(cur.left);
                valQueue.offer(cur.left.val + temp);
            }
            if (cur.right != null) {
                nodeQueue.offer(cur.right);
                valQueue.offer(cur.right.val + temp);
            }
        }
        return false;
    }

四、总结

1.从中序和后序遍历序列构造二叉树

106.从中序与后序遍历序列构造二叉树
搞清楚遍历数组/序列的性质：

后序遍历数组的最后一个元素代表根节点root，以此信息找到中序遍历数组的root下标值，就可以把中序数组分成左右子树部分。针对每个部分可以这样递归下去构造二叉树。

    public TreeNode buildTree(int[] inorder, int[] postorder) {
        int len = inorder.length;
        if (len == 0)
            return null;

        int left = 0;
        while (inorder[left] != postorder[len - 1])
            left++;

        TreeNode root = new TreeNode(postorder[len - 1]);
        root.left = buildTree(Arrays.copyOf(inorder, left), Arrays.copyOf(postorder, left));
        root.right = buildTree(Arrays.copyOfRange(inorder, left + 1, len), Arrays.copyOfRange(postorder, left, len - 1));
        return root;
    }

2.从前序和中序遍历序列构造二叉树

105.从前序与中序遍历序列构造二叉树
前序遍历数组的第一个元素代表根节点root，以此信息找到中序遍历数组的root下标值，就可以把中序数组分成左右子树部分。针对每个部分可以这样递归下去构造二叉树。

        public BinaryTree.TreeNode buildTree1(int[] preorder, int[] inorder) {
        int len = preorder.length;
        if (len == 0)
            return null;

        int index = 0;
        while (preorder[0] != inorder[index])
            index++;

        BinaryTree.TreeNode root = new BinaryTree.TreeNode(preorder[0]);
        root.left = buildTree(Arrays.copyOfRange(preorder, 1, index + 1), Arrays.copyOfRange(inorder, 0, index));
        root.right = buildTree(Arrays.copyOfRange(preorder, index + 1, len), Arrays.copyOfRange(inorder, index + 1, len));
        return root;
    }

还有一种迭代法，以后有空再实现吧。

3.填充每个节点的下一个右侧节点指针

116.填充每个节点的下一个右侧节点指针
法1：BFS+链表
首先，我第一次尝试写得是被注释掉的代码，可以看到代码很冗余，频繁使用hashmap，虽然很容易想到但是很麻烦。主要是我一开始没有注意到next这一个属性的内涵。暗示着什么？——链表。所以我第二次就用了链表的思维来做这一道题，但要注意每一层遍历前加个null给每层最后一个元素的next，如果不给的话，它会指向下一层的第一个元素。

    public Node connect(Node root) {
        if (root == null)
            return null;
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int sz = queue.size();
            queue.offer(null);
            Node cur = queue.poll();
            while (cur != null) {
                cur.next = queue.poll();
                if (cur.left != null) {
                    queue.offer(cur.left);
                }
                if (cur.right != null) {
                    queue.offer(cur.right);
                }
                cur = cur.next;//熟悉的链表操作。
            }
//            Map level = new HashMap<>();
//            int sz = queue.size();
//            for (int i = 0; i <= sz; i++) {
//                level.put(i, queue.poll());
//            }
//            for (int i = 0; i < sz; i++) {
//                level.get(i).next = level.get(i + 1);
//                if (level.get(i).left != null) {
//                    queue.offer(level.get(i).left);
//                    queue.offer(level.get(i).right);
//                }
//            }
        }
        return root;
    }

法2：BFS
我感觉大部分人都是想到这个，不用考虑链表指针指这指那的问题。这个方法也很值得学习，主要是要熟悉peek()方法的妙用。而且这种方法不用考虑每层最后一个元素的next了，默认为null。

    public Node connect1(Node root) {
        if (root == null)
            return null;
        Queue<Node> queue = new LinkedList<>();
        queue.offer(root);
        while (!queue.isEmpty()) {
            int sz = queue.size();
            for (int i = 0; i < sz; i++) {
                //取出队首
                Node cur = queue.poll();
                //进行连接
                if (i < sz - 1) {
                    cur.next = queue.peek();
                }
                if (cur.left != null) {
                    queue.add(cur.left);
                }
                if (cur.right != null) {
                    queue.add(cur.right);
                }
            }
        }
        return root;
    }

4.填充每个节点的下一个右侧节点指针Ⅱ

117.填充每个节点的下一个右侧节点指针Ⅱ
代码和上一道题一样。

5.二叉树的最近公共祖先

236.二叉树的最近公共祖先
本质就是搜索，搜索到两个目标节点后判断他们所处的位置来确定最近公共祖先。（注释掉的代码也能实现，只是会污染原二叉树。只是找个祖先而已，别把孩子弄没了啊）

    public TreeNode lowestCommonAncestor(TreeNode root, TreeNode p, TreeNode q) {
        if (root == null || root == p || root == q)
            return root;
//        root.left = lowestCommonAncestor(root.left, p, q);
//        root.right = lowestCommonAncestor(root.right, p, q);
//        if (root.left == null)
//            return root.right;
//        if (root.right == null)
//            return root.left;
//        return root;
        TreeNode left = lowestCommonAncestor(root.left, p, q);
        TreeNode right = lowestCommonAncestor(root.right, p, q);
        if (left == null)
            return right;
        if (right == null)
            return left;
        return root;
    }

6.二叉树的序列化和反序列化

297.二叉树的序列化与反序列化
值得记录，这是我在leetcode上做的第一道困难题，但这道题其实不难想，只是细节有点多。

    class Codec {

        // Encodes a tree to a single string.
        public String serialize(TreeNode root) {
            if (root == null)
                return "[]";
            StringBuffer sb = new StringBuffer();
            Queue<TreeNode> queue = new LinkedList<>();
            queue.offer(root);
            while (!queue.isEmpty()) {
                TreeNode cur = queue.poll();
                if (cur == null) {
                    sb.append("null,");
                    continue;
                }
                sb.append(cur.val + ",");
                queue.offer(cur.left);
                queue.offer(cur.right);
            }
            return "[" + sb.toString().substring(0, sb.length() - 1) + "]";
        }

        // Decodes your encoded data to tree.
        public TreeNode deserialize(String data) {
            data = data.trim().substring(1, data.length() - 1);
            if (data.length() == 0) {
                return null;
            }
            String[] parts = data.split(",");
            String item = parts[0];
            TreeNode root = new TreeNode(Integer.parseInt(item));
            Queue<TreeNode> nodeQueue = new LinkedList<>();
            nodeQueue.add(root);

            int index = 1;
            while (!nodeQueue.isEmpty()) {
                TreeNode node = nodeQueue.remove();

                if (index == parts.length) {
                    break;
                }

                item = parts[index++];
                item = item.trim();
                if (!item.equals("null")) {
                    int leftNumber = Integer.parseInt(item);
                    node.left = new TreeNode(leftNumber);
                    nodeQueue.add(node.left);
                }

                if (index == parts.length) {
                    break;
                }

                item = parts[index++];
                item = item.trim();
                if (!item.equals("null")) {
                    int rightNumber = Integer.parseInt(item);
                    node.right = new TreeNode(rightNumber);
                    nodeQueue.add(node.right);
                }
            }
            return root;
        }
    }

幸好在学二叉树之前学了队列&栈，这里做来做去都是BFS和DFS。

快要写完这篇文章的时候，居然收到了面试通知，这是我第一次收到啊……JVM、计算机网络、操作系统方面的知识几乎接近空白，框架也没复习，这该怎么搞呢，就当去取点经验把。现在还是先好好把数据结构与算法搞好。
next target:哈希表

---

五、闲话

最近压力有点大，也听了几天的梅特纳，突然会想换换音乐的口味。于是又回到了Danny Chan的歌声里，陈百强的歌声在我心里意味着美好、高贵、纯真与永恒，我一直都这么爱他。他是唯一一位在我什么心情都乐意聆听的歌者，在低落时刻则更需要他了。接下来分享的是两首很励志的歌，分别是《Greatest Love Of All》和《未唱的歌》。