力扣 354.俄罗斯套娃信封问题

问题描述

给你一个二维整数数组 envelopes ，其中 envelopes[i] = [wi, hi] ，表示第 i 个信封的宽度和高度。

当另一个信封的宽度和高度都比这个信封大的时候，这个信封就可以放进另一个信封里，如同俄罗斯套娃一样。

请计算最多能有多少个信封能组成一组“俄罗斯套娃”信封（即可以把一个信封放到另一个信封里面）。

注意：不允许旋转信封。

示例1：

输入：envelopes = [[5,4],[6,4],[6,7],[2,3]]
输出：3
解释：最多信封的个数为 3, 组合为: [2,3] => [5,4] => [6,7]。

示例2：

输入：envelopes = [[1,1],[1,1],[1,1]]
输出：1

提示：

• 1 <= envelopes.length <= 5000
• envelopes[i].length == 2
• 1 <= wi, hi <= 10^4

问题思路

思路1：递归

​ 该问题可以转化为一个寻找有向无环图中最长路径的问题。信封可看作一个个节点，信封 i 能装入到 j 可看作节点 i 到节点 j 有边。

​ 然后对每个节点按照深度优先进行遍历，计算其最长路径的长度（深度），该深度即为最大信封数。其中 deep = Integer.max(1 + countDeep(i), deep);

​ 实现代码如下，当输入规模比较大时，运行会超时。

class Solution {
	int maxDeep = 0; // 最大节点数
	boolean[][] matrix; // 邻接矩阵
	int n; // 节点数

	public int maxEnvelopes(int[][] envelopes) {
		// 初始化变量
		n = envelopes.length;
		matrix = new boolean[n][n];
		// 初始化邻接矩阵
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if ((envelopes[i][0] < envelopes[j][0]) && (envelopes[i][1] < envelopes[j][1])) {
					matrix[i][j] = true;
				}
			}
		}
		for (int i = 0; i < envelopes.length; i++) {
			maxDeep = Integer.max(1 + countDeep(i), maxDeep);			
		}
		return maxDeep;
	}
	public int countDeep(int node) {
		int deep = 0;
		for (int i = 0; i < n; i++) {
			if(matrix[node][i]) {
				deep = Integer.max(1 + countDeep(i), deep);			
			}
		}
		return deep;		
	}
}

思路2：动态规划法

​ 分析发现，在思路1中，存在大量重复计算，例如分别计算节点a、b的深度时，若节点a为b的前驱，那么countDeep(b)就会被计算两次，因此，考虑使用动态规划法，充分利用已计算的结果。

​ 设数组maxdeeps[n]，表示每个信封装入信封的个数，其中 n 为信封总数量。先对所有节点进行拓扑排序，再从后往前（或从前往后）遍历求解即可。

​ 实现代码如下，与思路1相同，当输入规模比较大时，运行会超时。

class Solution {
	boolean[][] matrix; // 邻接矩阵
	int n; // 节点数
	int[] inDegree = new int[n]; // 入度
	int[] topo; // 拓扑排序结果
	int[] deep; // 各节点的深度

	public int maxEnvelopes(int[][] envelopes) {
		// 初始化变量
		n = envelopes.length;
		matrix = new boolean[n][n];
		inDegree = new int[n];
		topo = new int[n];
		deep = new int[n];
        Arrays.fill(deep, 1);
		// 初始化邻接矩阵
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if ((envelopes[i][0] < envelopes[j][0]) && (envelopes[i][1] < envelopes[j][1])) {
					matrix[i][j] = true;
				}
			}
		}
		// 计算节点入度		
		for (int i = 0; i < n; i++) {
			for (int j = 0; j < n; j++) {
				if (matrix[j][i]) {
					inDegree[i]++;
				}				
			}
		}
		// 拓扑排序		
		topoSort();
		// 计算
		for (int i = n-1; i >= 0; i--) {
			for (int j = i-1; j >= 0; j--) {
				if (matrix[topo[j]][topo[i]]) {
					deep[topo[j]] = Integer.max(deep[topo[j]], deep[topo[i]] + 1);
				}
			}
		}		
		return Arrays.stream(deep).max().getAsInt();
	}
	
	public void topoSort() {
		Queue<Integer> queue = new LinkedList<Integer>();
		int index = 0;
        // 扫描所有的结点,将入度为0的结点入队
        for(int i = 0; i < n; i++) {
        	if(inDegree[i] == 0) {
        		queue.offer(i);
        	}                
        }            
        // 入度为0的结点出队且它的后继结点入度减1，将入度为0的节点入队
        while (!queue.isEmpty()) {
            int out = queue.poll().intValue();
            topo[index++] = out;
            for (int i = 0; i < n; i++) {
				if(matrix[out][i]) {
					if (--inDegree[i] == 0) {
						queue.offer(i);
					}
				}				
			}
        }
	}
}

思路3：动态规划法2

​ 进一步分析发现，如果将所有的信封按照信封的宽度 w 递增排列时，其顺序恰好满足拓扑排序。理由如下：

​ 设 i，j 为两个不同的信封，wi，wj分别为两个信封的宽度，且wi < wj，hi，hj 分别为两个信封的宽度。当hi ≥ hj 时，两节点间没有边，不存在优先次序，满足拓扑排序；当hi < hj 时，i 节点位于 j 节点之后，满足拓扑排序。对于 w 相等的两个节点，必没有边，因此也满足拓扑排序。

​ 排好序后，从后向前遍历也变得十分容易，只要保证后一个的 h 比前一个大即可。这里需要注意一点，当两信封宽度相等时，如果只看高度，可能会将两个宽度相等、高度递增排列的信封装在一起。因此为了解决这个问题，我们对宽度相同的信封按高度降序排列，这样就既满足拓扑排序，也可以简化问题。

​ 综上，该问题就转化为一个最长递增子序列的问题。首先对信封用高度作为第一关键字升序、宽度作为第二关键字降序进行排序。然后寻找序列 h 的最长严格递增子序列即可。

​ 实现代码如下，时间复杂度O(n^2)，运行时间295 ms。

class Solution {
	int n; // 节点数

	public int maxEnvelopes(int[][] envelopes) {
		// 初始化变量
		n = envelopes.length;
		int[] deep = new int[n];
		Arrays.fill(deep, 1);
		// 定义数组比较器
		Arrays.sort(envelopes, new Comparator<int[]>() {
            public int compare(int[] e1, int[] e2) {
                if (e1[0] != e2[0]) {
                    return e1[0] - e2[0];
                } else {
                    return e2[1] - e1[1];
                }
            }
        });
		// 计算
		for (int i = 1; i < n; i++) {
			for (int j = 0; j < i; j++) {
				if(envelopes[j][1] < envelopes[i][1]) {
					deep[i] = Integer.max(deep[i], deep[j] + 1);
				}
			}
		}
		return Arrays.stream(deep).max().getAsInt();
	}
}

思路4：基于二分查找的动态规划

​ 虽然思路3已经非常简单，但是仍有O(n^2)的时间复杂度，下面这种方法可以进一步优化：

​ 首先仍然对信封用高度作为第一关键字升序、宽度作为第二关键字降序进行排序，得到新的信封序列，取其中的高度序列 h 。

​ 设变量 minh[ i ] 表示当信封套娃数达到 i 时，末尾元素的最小高度。

​ 对高度序列进行一次扫描，并更新minh，更新满足以下规则：

• 如果当前 hi 大于 minh 中的最大值，则 hi 可以直接加到 minh 末尾。

• 否则，利用二分查找，找到 minh 中大于 hi 的最小值所在的下标 index ，令 minh[index] 等于 hi。

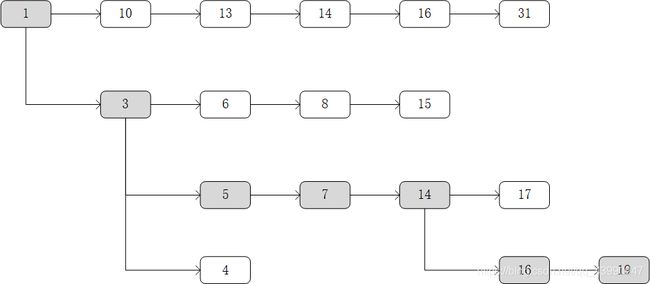
  这里举一个例子：

  设排序后的高度序列为{1, 10, 13, 3, 14, 6, 16, 31, 8, 5, 15, 7, 14, 17, 16, 19, 4}

  则 minh 数组更新过程如下图所示
  
  ​ 其中，阴影部分为 h 的最长递增子序列。

​ 实现代码如下，空间复杂度：O(n)，时间复杂度O(nlogn)。运行时间19 ms。

class Solution {
	int n; // 节点数

	public int maxEnvelopes(int[][] envelopes) {
		// 初始化变量
		n = envelopes.length;
		// 定义数组比较器
		Arrays.sort(envelopes, new Comparator<int[]>() {
            public int compare(int[] e1, int[] e2) {
                if (e1[0] != e2[0]) {
                    return e1[0] - e2[0];
                } else {
                    return e2[1] - e1[1];
                }
            }
        });
		// 计算
		List<Integer> minh = new ArrayList<Integer>();
		minh.add(envelopes[0][1]);
		for (int i = 0; i < n; i++) {
			int hi = envelopes[i][1];
			if (hi > minh.get(minh.size() - 1)) {
				minh.add(hi);
			}else {
				minh.set(binarySearch(minh,hi), hi);
			}
		}
		return minh.size();
	}
	
    // 二分查找
	public int binarySearch(List<Integer> minh, int hi) {
		int begin = 0, end = minh.size() - 1;
		while (begin < end) {
			int mid = (begin + end) / 2;
			if (minh.get(mid) < hi) {
				begin = mid + 1;
			}else {
				end = mid;
			}
		}
		return begin;
	}
}

总结

​ 本题的难点在于拓扑排序和求解最长递增子序列的长度上，如何减少时间复杂度是考虑的核心问题。

​ 通过单一维度的排序保证拓扑序列，通过动态规划以及二分查找降低求解时间。