【C数据结构】递归和非递归实现归并排序
文章目录
-
- 1、归并排序的实现(递归)
- 2、归并排序的实现(非递归)
- 3、归并排序的时间复杂度和空间复杂度
1、归并排序的实现(递归)
归并排序思路:归并排序主要通过分解,使得一定范围的序列变得有序,在有序之后,通过有序数组合并,最终形成有序序列。
归并排序最好用数组结构实现,因为链表的结构不方便确定中间序列。
那么如何通过分解,使得序列变得有序呢?
由于单个数字的序列是有序的,所以凭借这个特征,我们可以将序列不断拆分,再从1对1开始进行合并。
值得注意的是:
1.在合并两个有序数组时,在不改变容量的情况下,需要第三方数组才能合并。
2.在分割数组的时候,只能取[begin, mid] [mid+1, end] ,不能取[begin, mid-1] [mid, end],因为mid取值是取整的,偏近于begin,取第二种会造成死循环。
思路:
- 拆分序列。
- 合并序列
递归代码实现:
//归并排序
void _MergeSort(int* a, int begin, int end, int* tmp)
{
//拆分
//如果空序列或者只有一个数的序列,返回
if (begin >= end)
{
return;
}
//一直递归拆分,拆到序列剩两个数开始进行下面排序
int mid = (begin + end) / 2;
//[begin,mid] [mid+1,end]
_MergeSort(a, begin, mid, tmp);
_MergeSort(a, mid+1, end, tmp);
//合并 有序数组的合并
int begin1 = begin, end1 = mid;
int begin2 = mid+1, end2 = end;
int i = begin;
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] <= a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//把tmp中排序好的放入原来的地方
//因为begin1是从begin开始,i是从begin开始,所以两边指针都需要+begin
//之间数的个数是end-begin+1 或者 i-begin
memcpy(a+begin, tmp+begin, sizeof(int)*(end - begin + 1));
}
void MergeSort(int* a, int n)
{
//通过创建新的数组,
int* tmp = (int*)malloc(sizeof(int) * n);
if (tmp == NULL)
{
printf("malloc fail\n");
exit(-1);
}
_MergeSort(a, 0, n-1, tmp);
free(tmp);
tmp = NULL;
}
2、归并排序的实现(非递归)
想要实现非递归,首先需要理解递归的思想,归并排序的递归思想类似于二叉树的后序遍历,先分割再操作。
因为类似于后序遍历的实现,使得如果用栈或者队列来说非常麻烦,因为要保留一开始的大范围下标,而且要先使用小范围的下标。
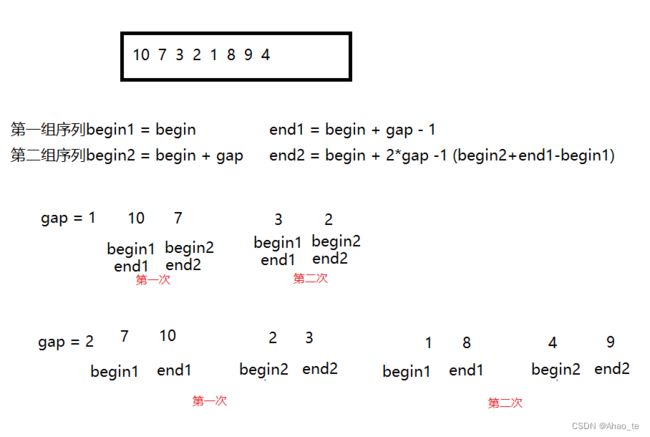
我们不难发现,归并排序既然要从小范围坐标开始,我们不如直接就通过循环从小坐标开始。
值得注意的是:以上情况都针对的是数组数量为2^n情况,也就是每次第一组和第二组数量都一样的情况,下面我们看看其它情况。
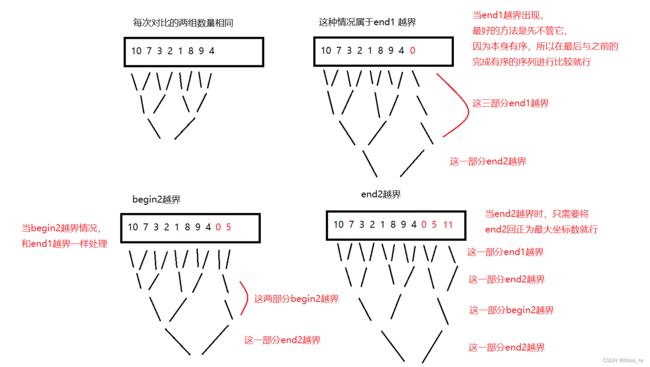
可以看到,每一种情况最后合并都只会出现两种情况,一种无越界,一种end2越界,而之前的越界都可以跳过这次比较,放到最后作为一个部分有序序列与一个完整有序序列进行比较合并。
非递归代码实现:
void MergeSortNonR(int* a, int size)
{
//建立第三方数组
int* tmp = (int*)malloc(sizeof(int) * size);
if (tmp == NULL)
{
perror("malloc fail");
exit(-1);
}
int gap = 1;
//分割
while (gap < size)
{
for (int begin = 0; begin < size; begin += 2 * gap)
{
int begin1 = begin, end1 = begin + gap - 1;
int begin2 = begin + gap, end2 = begin + 2 * gap - 1;
int i = begin;
//第一组end1越界
if (end1 > size - 1)
{
break;
}
//第二组begin2越界
if (begin2 > size - 1)
{
break;
}
//第二组end2越界
if (end2 > size - 1)
{
end2 = size - 1;
}
while (begin1 <= end1 && begin2 <= end2)
{
if (a[begin1] < a[begin2])
{
tmp[i++] = a[begin1++];
}
else
{
tmp[i++] = a[begin2++];
}
}
while (begin1 <= end1)
{
tmp[i++] = a[begin1++];
}
while (begin2 <= end2)
{
tmp[i++] = a[begin2++];
}
//再将tmp内的数考回a中
//每次拷贝一部分 这次比较的
memcpy(a + begin, tmp + begin, sizeof(int) * (i - begin));
}
gap*=2;
}
free(tmp);
tmp == NULL;
}
3、归并排序的时间复杂度和空间复杂度
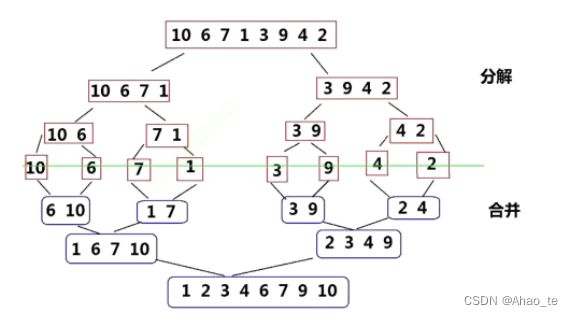
时间复杂度:
从归并排序的思路来看,拆分与合并逻辑结构都呈现树状结构,并且整个高度呈现LogN,在每一层都是N个数进行着比较,所以时间复杂度应该是O(N*logN)。
空间复杂度:
由于空间的可复用性,在递归实现中,tmp作为第三方储存为N,整个栈帧销毁为LogN,所以最后空间复杂度应该是O(n),而非递归不考虑栈帧销毁,只有tmp的储存消耗,最后空间复杂度是O(N)。
本章完